Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

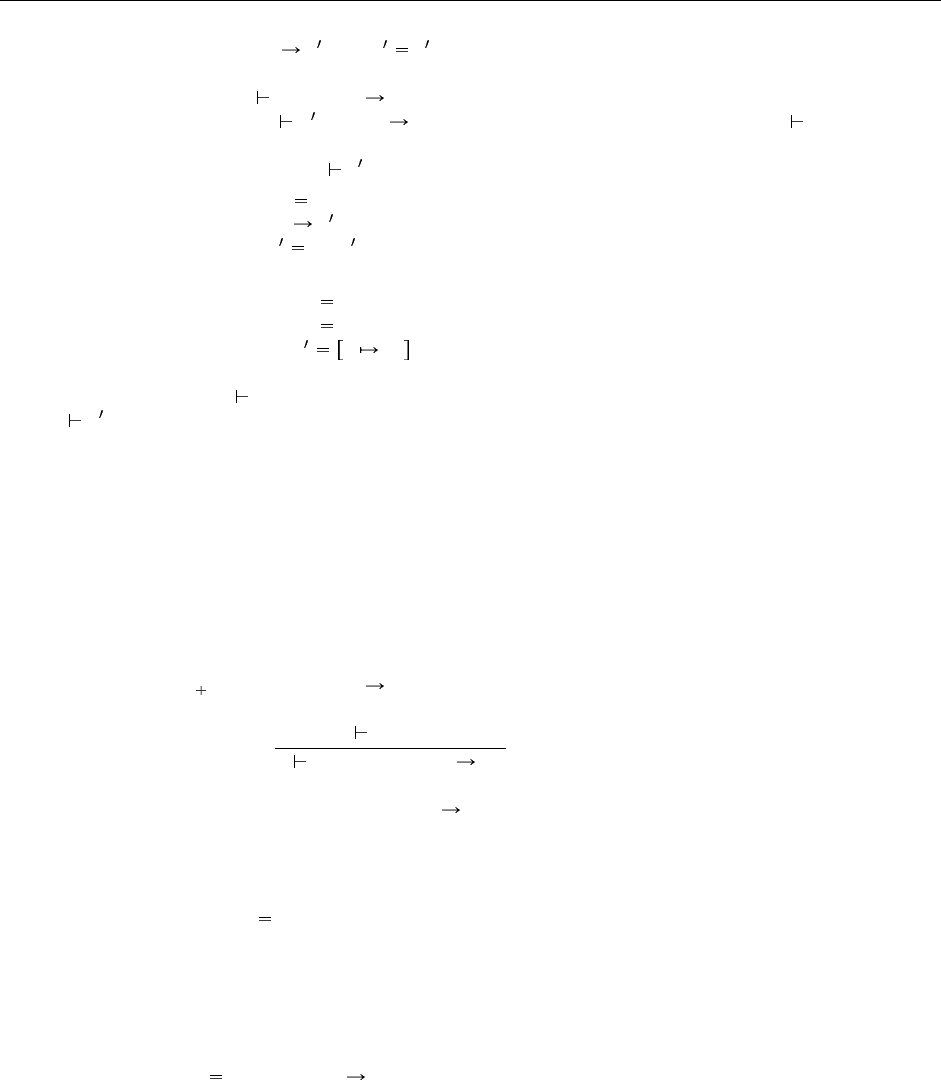
391

Подвариант E-App1: t

t t

Согласно предположениям для варианта T-App, в исходном дереве вывода типа есть подде-

рево с заключением Γ t

: T

. Применяем к этому утверждению предположение

индукции и получаем Γ t

: T

. Сочетая это с наблюдением, что Γ t

: T

(также одно из предположений в варианте T-App), получаем возможность применить пра-

вило T-App с заключением Γ t : T.

Подвариант E-App2: t

(т. е., t

является значением)

t v

Аналогично.

Подвариант E-AppAbs: t

λx:T

. t

t x v

С помощью леммы об обращении мы можем разобрать дерево вывода типа для λx:T

и получить Γ, x:T

: T

. Исходя из этого и леммы о подстановке (§9.3.8), получаем

Γ t : T

Варианты с булевскими константами и условными выражениями доказываются так же, как в 8.3.3.

9.3.10. Решение: Терм (λx:Bool. λy:Bool. y) (true true) не имеет правильного типа, но редуци-

руется к правильно типизированному (λy:Bool. y).

9.4.1. Решение: T-True и T-False — правила введения. T-If — правило удаления. T-Zero и T-Succ

— правила введения. T-Pred и T-IsZero — правила удаления. Решение, являются ли succ и pred

конструкциями введения или удаления, требует небольшого раздумья, поскольку можно считать, что

они создают и используют числа. Здесь ключевое наблюдение состоит в том, что при встрече pred и

succ образуют редекс. То же касается и iszero.

11.2.1. Решение: t

= (λx:Unit.x) unit

i 1

= (λf:Unit Unit. f(f(unit))) (λx:Unit.t

)

11.3.2. Решение:

Γ t

: T

Γ λ_:T

: T

(T-Wildcard)

(λ_:T

) v

(E-Wildcard)

Доказательство, что эти правила выводятся из определения сокращения, выглядит в точности как

доказательство Теоремы 11.3.1.

11.4.1. Решение: Первое задание не представляет труда: если мы разворачиваем приписывание типа

с помощью правила t as T (λx:T. x) t, то простая проверка показывает, что как правила типиза-

ции, так и правила вычисления для этой конструкции прямо выводятся из правил для абстракции и

применения функций.

Если же мы введем энергичную версию правила вычисления, то придется применить более изощрен-

ное правило удаления сахара, откладывающее вычисление, пока конструкция приписывания не будет

отброшена. Например, так:

t as T

def

(λx:Unit T. x unit) (λy:Unit. t) с новой переменной y

Разумеется, выбор типа Unit здесь не имеет значения: подошел бы любой тип.

Тонкость здесь заключается в том, что преобразование удаления сахара, будучи интуитивно пра-

вильным, не обладает в точности свойствами, которые требует Теорема 11.3.1. Так выходит потому,

что результат перевода исчезает за два шага вычисления, в то время как высокоуровневое правило

E-Ascribe срабатывает за один шаг. Это, однако, не должно нас удивлять: будем рассматривать уда-

ление сахара как простую форму компиляции, и заметим, что в скомпилированном виде почти любая

высокоуровневая конструкция требует многих шагов вычисления целевого языка почти для любой эле-

ментарной редукции в исходном языке. В таком случае требуется ослабить требования Теоремы 11.3.1,

и утверждать, что каждый шаг вычисления высокоуровневой конструкции должен соответствовать

некоторой последовательности низкоуровневых шагов:

rev. 104

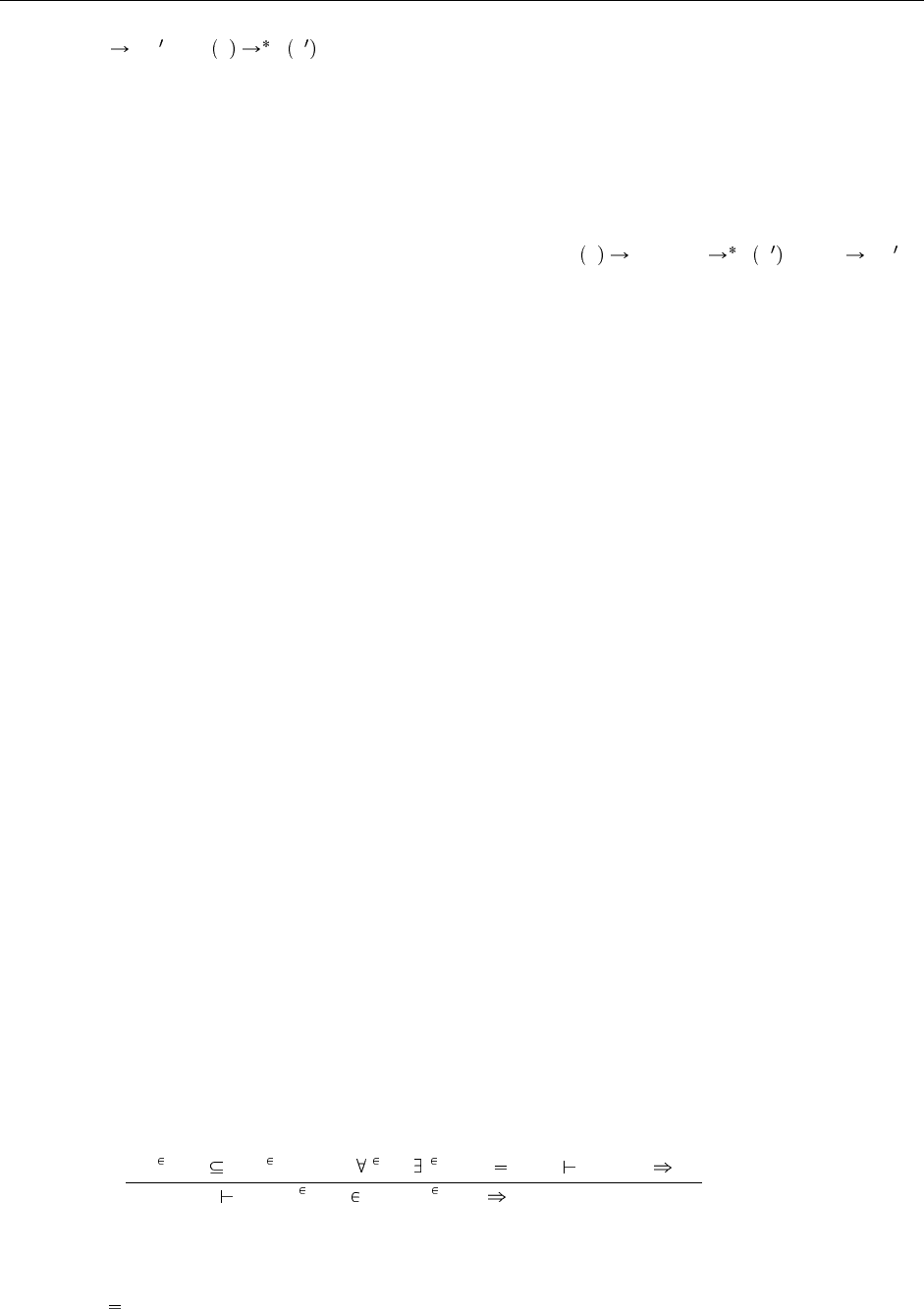
392

если t

t , то e t

e t

Последняя тонкость состоит в том, что другое направление — а именно, утверждение, что редук-

ции обессахаренного терма всегда можно отобразить «назад» в редукции исходного терма, — требует

некоторой осторожности при формулировке, поскольку вычисление обессахаренной конструкции при-

писывания типа занимает два шага, и после первого из них низкоуровневый терм не соответствует ни

удалению сахара из исходного терма с высокоуровневым приписыванием типа, ни терму, в котором это

приписывание отброшено. Верно, однако, то, что результат первой редукции обессахаренного терма

всегда можно «завершить», проведя еще один шаг вычисления и получив результат удаления сахара

для другого высокоуровневого терма. Формально говоря, если e t

s, то s

e t , где t

t .

11.5.1. Решение: Вот что требуется добавить:

let rec eval1 ctx t = match t with

...

| TmLet ( fi , x ,v1 , t2 ) when isval ctx v1 ->

termSubstTop v1 t2

| TmLet ( fi , x ,t1 , t2 ) ->

let t1 ’ = eval1 ctx t1 in

TmLet ( fi ,x ,t1 ’ , t2 )

...

let rec type of ctx t ->

match t with

...

| TmLet ( fi , x ,t1 , t2 ) ->

let tyT1 = typeof ctx t1 in

let ctx ’ = ad d b i n ding ctx x ( VarBin d ( tyT1 )) in

( ty peof ctx ’ t2 )

11.5.2. Решение: Это определение работает плохо. Для начала, оно изменяет порядок вычисления:

правила E-LetV и E-Let задают порядок вызова по значению, где t

в let t

in t

должно быть

вычислено и дать значение, прежде, чем мы сможем подставить его вместо x и начать работать над

. Кроме того, хотя корректность правила типизации T-Let при новом переводе сохраняется — это

прямо следует из леммы о подстановке (9.3.8), не-корректность типизации термов может потеряться.

Например, неверно типизированная форма

let x = unit ( unit ) in unit

переводится в типизированный терм unit: поскольку x не встречается в теле unit, неверно типизиро-

ванный терм unit(unit) просто исчезает.

11.8.2. Решение: Один из способов добавить типы к образцам для записей изображен на Рис. A.1.

Правило типизации для обобщенной конструкции let, T-Let, ссылается на отдельное отношение «ти-

пизации образцов», которое (с алгоритмической точки зрения) принимает на входе образец и тип, и, в

случае успеха, выдает контекст, содержащий связывания для переменных образца. Правило T-Let до-

бавляет этот контекст к текущему контексту Γ при проверке типов в теле t

. (Мы всюду предполагаем,

что множества переменных, связываемых в различных полях образца для записи, не пересекаются.)

Заметим, что при желании мы могли бы несколько улучшить правило типизации образцов, позво-

лив образцам указывать меньше полей, чем содержится в значении, с которым сопоставление будет

проводиться:

i 1..n

} {k

j 1..m

}

i 1..n

j 1..m

и p

: T

∆

i 1..n

} {k

j 1..m

} ∆

, . . . , ∆

(P-Rcd)

Если мы примем это правило, мы можем перестать считать форму проекции поля базовой конструк-

цией, поскольку теперь ее можно рассматривать как синтаксический сахар:

t.l

def

let {l=x}=t in x

rev. 104

393

{} let p (типизированные) Расширяет 11.8

Правила типизации образцов

x : T x:T (P-Var)

для каждого i p

: T

∆

i 1..n

} : {k

j 1..m

} ∆

, . . . , ∆

(P-Rcd)

Новые правила типизации Γ t : T

Γ t

p:T

∆ Γ, ∆ t

: T

Γ let p =t

in t

: T

(T-Let)

Рис. A.1. Типизированные образцы для записей

Лемма о сохранении для расширенной системы доказывается почти так же, как и для простого

типизированного лямбда-исчисления. Единственное требуемое расширение — лемма, связывающая от-

ношение типизации образцов с операцией сопоставления, осуществляемой при исполнении программы.

Если имеется подстановка σ и контекст ∆ с той же областью определения, что у σ, то Γ σ ∆

означает, что для каждого x dom σ , выполняется Γ σ x : ∆ x .

Лемма: Если Γ t : T и p : T T, то match p, t σ, где Γ σ ∆.

Введенная нами дополнительная нотация требует небольшого обобщения стандартной леммы о подста-

новке (9.3.8):

Лемма: Если Γ, ∆ t : T и Γ σ ∆, то Γ σt : T.

Теперь аргументация в лемме о сохранении для правила C-Let может следовать той же схеме, что и

раньше, с использованием новых лемм для случая C-Let.

11.9.1. Решение:

Bool

def

Unit+Unit

true

def

inl unit

false

def

inr unit

if t

then t

else t

def

case t

of inl x

=> t

| inr x

=>t

с новыми переменными x

и x

11.11.1. Решение:

equal =

fix

(λeq : Nat -> Nat -> Bool .

λm . Nat . λn : Nat .

if isze ro m then iszero n

else if iszero n then false

else eq ( pred m) ( pred n ));

equal : Nat -> Nat -> Bool

plus = fix (λp : Nat -> Nat -> Nat .

λm . Nat . λn : Nat .

if isze ro m then n else succ ( p ( pred m) n ));

plus : Nat -> Nat -> Nat

times = fix (λt : Nat -> Nat - > Nat .

λm . Nat . λn : Nat .

if isze ro m then 0 else plus n ( t ( pred m) n ));

times : Nat -> Nat -> Nat

fac t o rial = fix (λf: Nat -> Nat .

rev. 104

394

λm . Nat .

if isze ro m then 1 else times m ( f ( pred m )));

fac t o rial : Nat -> Nat

fac t o rial 5;

120 : Nat

11.11.2. Решение:

le trec plus : Nat -> Nat -> Nat =

λm . Nat . λn : Nat .

if isze ro m then n else succ ( plus ( pred m) n) in

le trec times : Nat - > Nat -> Nat =

λm . Nat . λn : Nat .

if isze ro m then 0 else plus n ( times ( pred m) n) in

le trec fac t orial : Nat - > Nat =

λm . Nat .

if isze ro m then 1 else times m ( f a c torial ( pred m )) in

fac t o rial 5;

120 : Nat

11.12.1. Решение: Сюрприз! На самом деле, теорема о продвижении не выполняется. Например, вы-

ражение head[T] nil[T] находится в тупике — никакое правило вычисления к нему не применимо, но

оно не значение. В полноразмерном языке программирования с такой ситуацией можно справиться, ес-

ли заставить head[T] nil[T] порождать исключение вместо тупикового состояния: мы рассматриваем

исключения в Главе 14.

11.12.2. Решение: Не от всех: если мы уберем аннотацию на nil, то потеряем теорему о единственно-

сти типов. С операционной точки зрения, когда программа проверки типов видит nil, она знает, что

требуется присвоить ему тип List T для некоторого T, однако она не знает, какой T выбрать. Разу-

меется, более изощренные алгоритмы типизации, вроде используемого в компиляторе OCaml, умеют

догадываться, какой тип нужен. Мы вернемся к этому вопросу в Главе 22.

12.1.1. Решение: При рассмотрении применений. Допустим, мы пытаемся доказать, что терм t

нормализуем. Из предположения индукции нам известно, что нормализуемы t

и t

; пусть их нор-

мальные формы будут v

и v

. Из леммы об обращении отношения типизации (9.3.1) нам известно, что

имеет тип T

для некоторых T

и T

. Следовательно, по лемме о канонических формах

(9.3.4), v

обязан иметь вид λx:T

. Но сведение t

к (λx:T

) t

не дает нам нормальной

формы, поскольку мы можем применить правило E-AppAbs, получая x t

, и для завершения

доказательства требуется продемонстрировать, что этот терм нормализуем. Однако этого мы сделать

не можем, поскольку в общем случае этот терм может оказаться больше, чем исходный терм t

(при

подстановке возникает столько копий t

, сколько было вхождений переменной x в t

12.1.7. Решение: Определение 12.1.2 расширяется двумя дополнительными пунктами:

• R

Bool

t тогда и только тогда, когда вычисление t завершается.

• R

t тогда и только тогда, когда вычисление t завершается, R

t.1 и R

t.2 .

В доказательство Леммы 12.1.4 также вводится дополнительный пункт:

• Допустим, T T

для некоторых T

и T

. Для направления «слева направо» ( ) мы пред-

полагаем R

t и должны показать R

t , где t t . Из определения R

мы знаем, что

t.1 и R

t.2 . Правила вычисления E-Proj1 и E-Proj2 говорят нам, что t.1 t .1 и

t.2 t .2, так что, по предположению индукции, R

и R

. Отсюда, по определению

, получаем R

t . Направление «справа налево» ( ) доказывается аналогично.

Наконец, нужно добавить несколько вариантов (по одному на каждое новое правило типизации) в

доказательство Леммы 12.1.5:

rev. 104

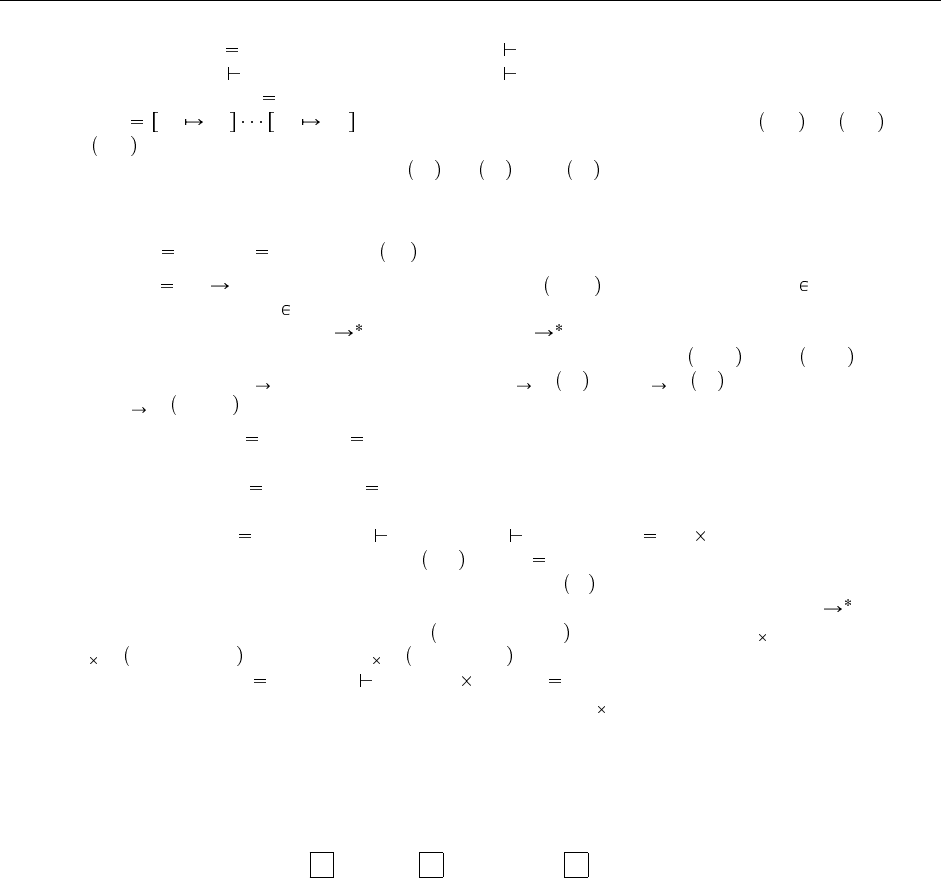
395

Вариант T-If: t if t

then t

else t

Γ t

: Bool

Γ t

: T Γ t

: T

где Γ x

, ..., x

Пусть σ x

. Согласно предположению индукции, R

Bool

σt

, R

σt

и R

σt

. По Лемме 12.1.3, σt

, σt

и σt

нормализуемы; обозначим их значения v

, v

. Согласно Лемме 12.1.4, имеем R

Bool

, R

, и R

. Кроме того, ясно, что терм σt

сам по себе нормализуем.

Продолжаем по индукции по T.

• Если T A или T Bool, то R

σt немедленно следует из того, что σt нормализуем.

• Если T T

, то нам требуется показать R

σt s для произвольного s R

. Так

что предположим s R

. Тогда, по правилам вычисления для условных выражений,

мы видим, что либо σt s v

s, либо σ t s v

s, в зависимости от того, равен

ли v

значению true или значению false. Но мы знаем, что R

s и R

s (по

определению R

) и, кроме того, что R

и R

. По Лемме 12.1.4,

σ t s , как и требуется.

Вариант T-True: t true T Bool

Утверждение следует непосредственно.

Вариант T-False: t false T Bool

Утверждение следует непосредственно.

Вариант T-Pair: t {t

} Γ t

: T

Γ t

: T

T T

Согласно предположению индукции, R

σt

для i 1, 2. Пусть нормальной формой для

каждого t

будет v

. Заметим, что, по Лемме 12.1.4, R

Согласно правилам вычисления для первой и второй проекции, {σt

, σt

}.i v

откуда, по Лемме 12.1.4, получаем R

{σt

, σt

}.i . Определение R

дает нам

{σt

, σt

} , то есть, R

σ{t

, t

} .

Вариант T-Proj1: t t

.1 Γ t

: T

T T

Утверждение непосредственно следует из определения R

13.1.1. Решение:

a={







} b={







}

0 0 0

13.1.2. Решение: Нет — вызовы lookup с любым индексом, кроме заданного в update, теперь будут

зацикливаться. Дело в том, что требуется искать значение, хранившееся в a до того, как мы поместили

в ячейку новую функцию. В противном случае, когда нам потребуется вызвать поиск, мы обнаружим

в ячейке новую функцию, а не исходную.

13.1.3. Решение: Допустим, в языке имеется примитив free, принимающий в качестве аргумента ссы-

лочную ячейку, и освобождающий занимаемую ей память так, чтобы (скажем) следующая же операция

выделения получила тот же самый участок памяти. Тогда программа

let r = ref 0 in

let s = r in

free r ;

let t = ref true in

t := false ;

succ (! s )

при вычислении приведет к тупиковому терму succ false. Заметим, что в возникновении проблемы

ключевую роль играют псевдонимы: они не дают нам отслеживать ошибочные операции освобожде-

ния, просто запрещая free в ситуациях, когда переменная r присутствует в остатке вычисляемого

выражения в качестве свободной.

rev. 104

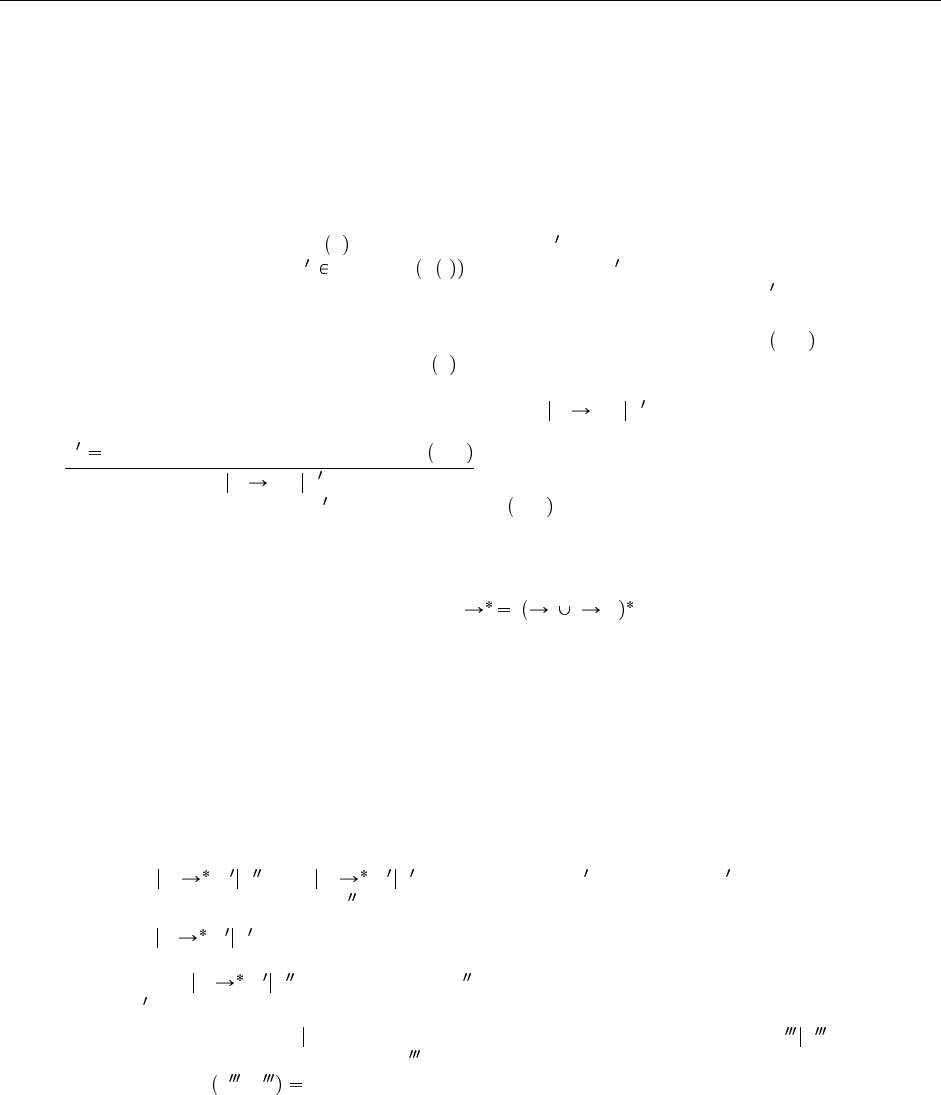
396

Примеры такого рода легко получить в языке вроде C, где применяется ручное управление памятью

(наш конструктор ref соответствует malloc в C, а наша операция free — упрощенная версия free из

C).

13.3.1. Решение: Простое формальное описание сборки мусора может выглядеть так:

1. Конечность памяти можно смоделировать, считая множество адресов L конечным.

2. Определяем достижимость адресов следующим образом. Обозначаем множество адресов: упо-

минаемых в t, через locations t . Говорим, что адрес l достижим за один шаг из адреса l при

состоянии памяти µ, если l locations µ l . Говорим, что l достижим из l, если существует

конечная последовательность адресов, начинающаяся с l и заканчивающаяся l , так, что каждый

следующий адрес достижим из предыдущего за один шаг. Наконец, определяем множество адре-

сов, достижимых из терма t при состоянии памяти µ (записывается reachable t, µ ), как адреса,

достижимые при состоянии µ из locations t .

3. Моделируем действие сборки мусора как отношение t µ

t µ , определяемое следующим пра-

вилом:

µ µ ограниченное областью reachable t, µ

t µ

E-GC

(т. е., область определения µ – только reachable t, µ , а его значение в каждой точке области

определения такое же, как у µ.)

4. Определяем последовательности вычисления как последовательности обычных шагов вычисле-

ния, перемежаемых шагами сборки мусора:

def

. Обратите внимание, что мы не

просто добавляем правило GC в обыкновенное одношаговое отношение вычисления: важно, что

мы производим сборку мусора только на «внешнем уровне», где виден весь вычисляемый в дан-

ный момент терм. Если бы мы разрешили сборку мусора, например, «внутри» вычисления левой

стороны терма-применения, мы бы могли по ошибке собрать и заново использовать адреса, кото-

рые упоминаются на правой стороне, поскольку, глядя на левую сторону, мы не могли бы увидеть,

что они все еще доступны.

5. Доказываем корректность нашего определения вычисления, показывая, что оно не изменяет окон-

чательные результаты, за исключением возможности исчерпания памяти:

(a) Если t µ

t µ , то t µ t µ для некоторого µ , такого, что µ имеет более широкую

область определения, чем µ , и там, где они оба определены, они совпадают.

(b) Если t µ t µ то

i. либо t µ

t µ для некоторого µ , имеющего более узкую область определения, чем

µ , и там, где они оба определены, они совпадают;

ii. либо вычисление t µ исчерпывает память — т. е., достигает состояния t µ , такого, что

следующий шаг вычисления t требует выделения памяти, но это невозможно, так как

reachable t , µ L.

Этот простой подход к описанию сборки мусора не учитывает некоторые свойства реальной памяти,

например, то, что хранение различных видов значений, как правило, требует различного количества

памяти, а также некоторые сложные языковые конструкции, например, финализаторы (подпрограммы,

которые исполняются, когда система исполнения собирается освободить структуры данных, к которым

они приписаны) и слабые указатели (указатели, которые не считаются «настоящими ссылками» на

структуру данных, так что эта структура может быть освобождена, даже если на нее имеются слабые

указатели). Более тщаетельное отображение сборки мусора средствами операционной семантики можно

найти у Моррисета и др. (Morrisett et al. 1995).

13.4.1. Решение:

rev. 104

397

let r

= ref (λx: Nat .0) in

let r

= ref (λx: Net .(! r

)x) in

:= (λx: Nat .(! r

)x );

);

13.5.2. Решение: Допустим, µ — состояние памяти с единственным адресом l

µ l λx:Unit.(!l)(x)

а Γ — пустой контекст. Тогда µ правильно типизировано по отношению к обеим следующим структурам

типизации памяти:

l:Unit Unit

l:Unit (Unit Unit)

13.5.8. Решение: В этой системе есть правильно типизированные термы, не являющиеся сильно нор-

мализуемыми. Один пример был приведен в Упражнении 13.1.2. Вот еще один:

t1 = λr : Ref ( Unit - > Unit )

(r := (λx: Unit . (! r)x );

(! r) unit );

t2 = ref (λx : Unit . x );

Применение t1 к t2 дает (правильно типизированный) расходящийся терм.

В общем случае, можно определять произвольные рекурсивные функции через ссылки с помощью

следующей последовательности шагов. (Такой метод действительно используется в некоторых реали-

зациях функциональных языков.)

1. Выделяем ссылочную ячейку и инициализируем ее функцией-заглушкой нужного нам типа:

fact

ref

= ref (λn: Nat .0);

fact

ref

: Ref (Nat - > Nat )

2. Определяем тело функции, которая нам нужна, используя для рекурсивных вызовов обращение

к содержимому ячейки:

fact

body

λn : Nat .

if isze ro n then 1 else times n ((! fact

ref

)( pred n ));

fact

body

: Nat -> Nat

3. Устанавливаем тело «на место», в ссылочную ячейку:

fact

ref

:= fact

body

;

4. Обращаемся к содержимому ячейки и используем его, как нам требуется:

fact = fact

ref

;

fact 5;

120 : Nat

14.1.1. Решение: Указание ожидаемого типа в error уничтожит свойство сохранения типов. Например,

правильно типизированный терм

(λx : Nat .x) ((λy : Bool .5) ( error as Bool ));

(где error as T — синтаксис для указания типа в исключениях) за шаг превратится в неверно типи-

зированный

(λx : Nat .x) ( error as Bool );

rev. 104

398

Когда правила вычисления распространяют error от того места, где он возник, до верхнего уровня

программы, нам приходится рассматривать его как терм, имеющий различные типы. Гибкость правила

T-Error нам это позволяет.

14.3.1. Решение: В Определении Стандартного ML (Milner, Tofte, Harper and MacQueen 1997; Milner

and Tofte 1991b) формально описывается тип exn. Подобный подход можно также найти у Харпера и

Стоуна (Harper and Stone 2000).

14.3.2. Решение: См. Леруа и Пессо (Leroy and Pessaux 2000).

14.3.3. Решение: См. Харпер и др. (Harper et al. 1993).

15.2.1. Решение:

{x:Nat,y:Nat,z:Nat} <: {y:Nat,x:Nat,z:Nat}

S-RcdPerm

{y:Nat,x:Nat,z:Nat} <: {y:Nat}

S-RcdWidth

{x:Nat,y:Nat,z:Nat} <: {y:Nat}

S-Trans

15.2.2. Решение: Существует множество других деревьев вывода с тем же самым заключением. Вот

одно из них:

f : Rx Nat

Rxy <: Rx

S-RcdWidth

Nat <: Nat

S-Refl

Rx Nat <: Rxy Nat

S-Arrow

f : Rxy Nat

T-Sub

xy : Rxy

f xy : Nat

T-App

Вот еще одно:

f : Rx Nat

xy : Rxy

T-Rcd

Rxy <: Rx

S-RcdWidth

Rx <: Rx

S-Refl

Rxy <: Rx

S-Trans

xy : Rx

T-Sub

f xy : Nat

T-App

В сущности, как можно догадаться по второму примеру, в этом исчислении имеется бесконечно много

деревьев вывода для любого выводимого утверждения.

15.2.3. Решение:

1. Их шесть: {a:Top,b:Top}, {b:Top,a:Top}, {a:Top}, {b:Top}, {} и Top.

2. Пусть, например,

{}

{a:Top}

{a:Top,b:Top}

{a:Top,b:Top,c:Top}

и т. д.

3. Пусть, например, T

Top, T

Top, и т. д.

15.2.4. Решение: (1) Нет. Если бы такой тип существовал, это был бы либо тип записей, либо функ-

циональный тип (очевидно, это не может быть Top). Но тип записей не являлся бы подтипом никакого

функционального типа, и наоборот. (2) Тоже нет. Если бы существовал такой функциональный тип

, тип его области определения T

должен был бы быть подтипом всякого другого типа S

, а это,

как мы только что убедились, невозможно.

rev. 104

399

15.2.5. Решение: Добавление этого правила было бы неверным шагом, если мы желаем сохранить

имеющуюся семантику вычисления. Новое правило позволило бы нам вывести, например, Nat Bool

<: Nat. Отсюда получалось бы, что тупиковый терм (succ (5,true)) правильно типизирован, и нару-

шается теорема о продвижении. Такое правило безопасно в семантике на основе преобразования типов

(см. 15.6), но даже там возникают некоторые алгоритмические сложности при проверке наследования.

15.3.1. Решение: Добавляя в отношение наследования лишние пары, мы можем потерять как продви-

жение, так и сохранение. Например, добаление аксиомы

{x:{}} <: {x:Top Top}

позволяет вывести Γ t : Top, где t = ({x={}}.x){}. Но t {}{}, который не типизируется —

нарушается свойство сохранения. С другой стороны, если мы добавим аксиому

{} <: Top Top

то терм {}{}, наоборот, будет типизируем, но это тупиковый терм, не являющийся значением — нару-

шается свойство продвижения.

Напротив, исключение пар из отношения наследования никакого вреда не причиняет. В формули-

ровке теоремы о продвижении отношение типизации упоминается лишь в предпосылках, так что ограни-

чение отношения наследования, влекущее ограничение отношения типизации, может только упростить

задачу доказательства этой теоремы. В случае теоремы о сохранении мы можем особенно беспокоиться,

что потеря свойства транзитивности создаст нам проблемы. Однако таких проблем не возникает, с ин-

туитивной точки зрения, потому, что правило транзитивности не играет существенной роли в системе.

А именно, что транзитивность можно восстановить при помощи правила включения T-Sub. Например,

вместо

Γ t : S

S <: U

U <: S

S <: T

S-Trans

Γ t : T

T-Sub

всегда можно написать

Γ t : S

S <: U

Γ t : U

T-Sub

U <: T

Γ t : T

T-Sub

15.3.2. Решение:

1. Индукция по деревьям вывода наследования. Рассмотрев правила наследования на Рис. 15.1 и

15.3, мы видим, что последнее правило при выводе S <: T

должно быть одно из S-Refl,

S-Trans или S-Arrow.

Если последнее правило S-Refl, то результат следует немедленно (поскольку в этом случае

S=T

, а из рефлексивности мы можем вывести T

<: T

и T

<: T

Если последнее правило S-Trans, то у нас имеются подвыводы с заключениями S <: U и U <:

для некоторого типа U. Применяя предположение индукции к второму подвыводу, мы

видим, что U обязан иметь вид U

, причем T

<: U

и U

<: T

. Поскольку U — функцио-

нальный тип, мы можем применить предположение индукции к первому подвыводу, и получить S

= S

, причем U

<: S

и S

<: U

. Наконец, применяя дважды правило S-Trans, мы можем

собрать вместе полученные нами утверждения и получить T

<: S

(из T

<: U

и U

<: T

) и

<: T

(из S

<: U

и U

<: T

Если последнее правило S-Arrow, то S имеет требуемый вид, а заключения непосредственных

подвыводов — в точности те утверждения, которые нам требуется получить о частях S.

rev. 104

400

2. Индукция по деревьям вывода. Снова рассматривая правила наследования, убеждаемся, что

последним правилом в выводе S <: {l

i 1..n

} может быть S-Refl, S-Trans, S-RcdWidth,

S-RcdDepth либо S-RcdPerm. Вариант S-Refl тривиален. В вариантах S-RcdWidth, S-

RcdDepth и S-RcdPerm требуемое утверждение следует непосредственно.

Если последнее правило S-Trans, у нас должны быть подвыводы с заключениями S <: U и U <:

i 1..n

} для некоторого типа U. Применяя предположение индукции ко второму подвыводу,

мы видим, что U имеет вид {u

a 1..o

}, причем {l

i 1..n

} {u

a 1..o

} и U

<: T

для каждого

= u

. Поскольку теперь мы знаем, что U — тип записей, мы можем применить предположение

индукции к первому подвыводу и получить S = {k

j 1..m

}, причем {u

a 1..o

} {k

j 1..m

} и S

<: U

для каждого u

. Переупорядочивая эти утверждения, получаем {l

i 1..n

} {k

j 1..m

}

по транзитивности отношения «подмножество», и S

<: T

по S-Trans для каждого l

= k

, по-

скольку каждая метка в типе T должна также присутствовать в U (т. е., l

должно равняться u

для некоторого a), и тогда нам известно, что S

<: U

и U

<: T

. (Странные имена метаперемен-

ных в этом доказательстве неизбежны: иначе просто не хватает латинских букв.)

15.3.6. Решение: Обе части доказываются индукцией по деревьям вывода типов. Мы приводим дока-

зательство только первой части.

Рассматривая правила типизации, мы видим, что последним правилом при выводе v : T

может быть только T-Abs или T-Sub. Если это T-Abs, то необходимый нам результат непосредственно

следует из предпосылки правила. Предположим тогда, что последнее правило T-Sub.

Из предпосылок T-Sub имеем v : S и S <: T

. По лемме об обращении (15.3.2), S имеет вид

. Теперь результат следует из предположения индукции.

16.1.2. Решение: Часть (1) доказывается путем прямолинейной индукции по структуре S.

Доказывая часть (2), заметим сначала, что, если существует какой-либо вывод S <: T, то, согласно

части (1), существует вывод без использования рефлексивности. Мы можем доказать наше утвержде-

ние индукцией по размеру дерева вывода S <: T, не использующего рефлексивность. Заметим, что

мы строим индукцию по размеру дерева, а не по его структуре, как обычно делали до сих пор. Это

необходимо потому, что в случаях функциональных типов и типов-записей мы применяем индуктивное

предположение к заново построенным деревьям вывода, которые не являются поддеревьями исходного

вывода.

Если последнее правило вывода не является экземпляром S-Trans, результат прямо следует из

индуктивного предположения (т. е., по предположению индукции, все подвыводы последнего правила

можно заменить выводами без использования транзитивности; поскольку последнее правило также не

использует транзитивность, весь вывод оказывается от нее свободен). Предположим тогда, что послед-

нее правило в выводе — S-Trans, т. е., что у нас есть подвыводы с заключениями S <: U и U <: T,

для некоторого U. Рассмотрим варианты пар последних правил в обоих подвыводах.

Вариант Что угодно/ S-Top: T Top

Если правое поддерево заканчивается на S-Top, то результат следует немедленно, поскольку S <: Top

можно вывести независимо от формы S.

Вариант S-Top/ Что угодно: U Top

Если левое поддерево заканчивается на S-Top, мы замечаем, что, согласно предположению индукции,

можно предположить, что правое поддерево свободно от транзитивности. Рассмотрев правила наследо-

вания, мы видим, что последним правилом в этом поддереве всегда будет S-Top (мы уже исключили

случай рефлексивности, а все остальные правила требуют, чтобы U был либо функциональным типом,

либо типом записей). Нужный нам результат следует по S-Top.

Вариант S-Arrow/S-Arrow: S S

U U

T T

<: S

<: U

<: T

Используя S-Trans, мы можем построить выводы T

<: S

и S

<: T

, исходя из данных нам подвыво-

дов. Более того, эти выводы строго короче исходного вывода, так что мы можем применить индуктивное

предположение и получить выводы T

<: S

и S

<: T

без использования транзитивности. Сочетая

их с правилом S-Arrow, получаем вывод S

<: T

без транзитивности.

Вариант S-Rcd/ S-Rcd:

Подобным же образом.

rev. 104