Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

411

3 : Nat

hd ( tl ( tl l ))

1 : Nat

20.1.2. Решение:

fib = fix (λf : Nat -> Nat - > Stream . λm : Nat . λn : Nat . λ_: Unit .

{n , f n ( plus m n )}) 0 ;

fib : Str eam

20.1.3. Решение:

Co unter = µC. { get : Nat , inc : Unit - >C dec : Unit - >C ,

reset : Unit - > C backup : Unit - > C};

c = let create =

fix (λcr : {x: Nat , b: Nat }- > C ounter . λs: {x : Nat ,b: Nat }.

{ get = s .x ,

inc = λ_: Unit . cr {x= succ (s.x ) ,b=s . b },

dec = λ_: Unit . cr {x= pred (s.x ) ,b=s . b },

ba ckup = λ_: Unit . cr {x = s.x ,b= s .x},

reset = λ_ : Unit . cr {x=s .b ,b= s .b } })

in crea te {x =0 , b =0};

c : Counte r

20.1.4. Решение:

D = µX. < nat : Nat , bool : Bool , fn :X - >X >;

lam = λf :D ->D . <fn =f > as D ;

ap = λf :D . λa:D .

case f of

<nat =n > => div erge

unit

| < bool =b > = > diverg e

unit

| < fn =f > = > f a ;

ifd = λb : D. λt: D . λe :D.

case b of

<nat =n > => div erge

unit

| < bool =b > = > ( if b then t else e)

| < fn =f > = > diverg e

unit ;

tru = <bool = true > as D;

fls = <bool = false > as D;

ifd fls one zero ;

<nat =0 > as D : D

ifd fls one fls

< bool = false > as D : D

Читатели, обеспокоенные тем, что в этой системе мы можем закодировать неверно типизированные тер-

мы, должны заметить, что мы всего лишь построили структуру данных для представления объектного

языка бестиповых термов внутри метаязыка простого типизированного лямбда-исчисления с рекурсив-

ными типами. То, что это оказалось возможным, не удивительнее, чем тот факт (используемый нами в

главах, описывающих реализации, на протяжении всей книги), что термы различных типизированных

и бестиповых вариантов лямбда-исчислений могут быть представлены в виде структур данных ML.

20.1.5. Решение:

rev. 104

412

lam = λf :D ->D . <fn =f > as D ;

ap = λf :D . λa:D . case f of

<nat =n > => div erge

unit

| < fn =f > = > f a

| < rcd =r > = > diverge

unit ;

rcd = λfield s : Nat ->D . <rcd = fields > as D;

prj = λf : D. λn: Nat . case f of

<nat =n > => div erge

unit

| < fn =f > = > diverg e

unit

| < rcd =r > = > r n ;

myrcd = rcd (λn : Nat . if iszero n then zro

else if iszero ( pred n) then one

else diverg e

unit );

20.2.1. Решение: Вот наиболее интересные примеры в изорекурсивной форме:

Hu ngry = µA. Nat -> A;

f = fix (λf: Nat - > Hungr y . λn : Nat . fold [ Hungry ] f );

ff = fold [ Hungry ] f ;

ff1 = ( unfold [ Hungry ] ff ) 0;

ff2 = ( unfold [ Hungry ] ff1 ) 2;

fix

λf :T ->T.

(λx :(µA.A -> T ). f (( unfold [µA .A ->T ] x ) x ))

( fold [µA .A ->T ] (λx :(µA .A ->T ). f (( unfold [µA .A ->T ] x ) x )));

D = µX. X -> X ;

lam = λf :D ->D . fold [D ] f ;

ap = λf :D . λa:D . ( unfo ld [D ] f ) a ;

Co unter = µC. { get : Nat , inc : Unit - >C };

c = let create = fix (λcr : { x : Nat } - > Counter . λs: {x: Nat }.

fold [ Count er ]

{ get = s.x ,

inc = λ_ : Unit . cr {x = succ ( s . x )}})

in crea te {x =0};

c1 = ( unfo ld [ Coun ter ] c ). inc unit ;

( un fold [ Counter ] c1 ). get ;

21.1.7. Решение:

a E

a, b a, c

a a E

a, c a, b

b a E

b, c a, b

c a, b E

a, b, c a, b, c

-замкнутыми множествами являются a и a, b, c . E

-консистентны , a и a, b, c . Наименьшая

неподвижная точка E

равна a . Наибольшая неподвижная точка равна a, b, c .

21.1.9. Решение: Чтобы доказать принцип обыкновенной индукции на натуральных числах, мы дей-

ствуем следующим образом. Определяем порождающую функцию F ℘ N ℘ N как

F X 0 i 1 i X

Теперь предположим, что у нас есть предикат (т. е., множество чисел) P , такое, что P 0 , и из P i

следует P i 1 . Тогда из определения F нетрудно видеть, что F P P , т. е., что множество P F -

замкнуто. Согласно принципу индукции, µF P . Однако µF равняется всему множеству натуральных

чисел (в сущности, это можно воспринимать как определение множества натуральных чисел), так что

P n верно для всех n N.

В случае лексикографической индукции, определяем F ℘ N N ℘ N N как

F X m, n m , n m, n , m , n X

rev. 104

413

Теперь допустим, что у нас есть предикат (т. е., множество пар чисел) P , такой, что всегда, когда

P m , n для всех m , n m, n , мы имеем также P m, n . Как и раньше, из определения F нетруд-

но увидеть, что F P P , т. е., что множество P F -замкнуто. Согласно принципу индукции, µF P .

Чтобы завершить доказательство, нужно проверить, что µF действительно совпадает с множеством

всех пар чисел (здесь единственный нетривиальный шаг рассуждения). Это можно доказать в два

шага. Сначала мы замечаем, что множество N N F -замкнуто (это непосредственно следует из опре-

деления F ). Во-вторых, мы доказываем, что ни одно собственное подмножество N N не является

F -замкнутым — т. е., что N N является наименьшим F -замкнутым множеством. Чтобы увидеть это,

предположим, что имеется некоторое меньшее F -замкнутое множество Y , и пусть m, n будет наимень-

шая пара, не принадлежащая Y ; согласно определению F , мы видим, что F Y Y , т. е., множество

Y незамкнуто — противоречие.

21.2.2. Решение: Определим дерево как частичную функцию T 1, 2 , , Top , удовлетворя-

ющую следующим ограничениям:

• T определена;

• Если определена T π, σ , то определена T π .

Заметим, что вхождения символов , , Top в вершинах дерева никак не ограничены — например,

вершина с меткой Top может иметь нетривиальных потомков, и т. п. Как и в §21.2, мы используем

символы , и Top также и в качестве имен операций над деревьями.

Множество всех деревьев берется как универсум U. Порождающая функция F основана на знакомой

нам грамматике для типов:

F X Top

, T

Из определений T и U нетрудно видеть, что T U , так что сравнение множеств в интересующих нас

уравнениях, T νF и T

µF , имеет смысл. Остается проверить, что эти уравнения истинны.

T νF следует по принципу коиндукции из того, что множество T F -консистентно. Чтобы получить

νF T , требуется проверить для всякого T νF два последних условия из Определения 21.2.1. Это

можно сделать при помоши индукции по длине π.

µF T

следует по принципу индукции из того, что множество T

F -замкнуто. Чтобы получить

µF , мы доказываем, индукцией по размеру T, что из T T

следует T µF . (Размер дерева можно

определить как длину наибольшей последовательности π 1, 2 , для которой определена T π .)

21.3.3. Решение: Пара Top, Top Top не лежит в νS. Чтобы увидеть это, обратите внимание, что,

по определению S, эта пара не принадлежит S X ни для какого X. Таким образом, нет ни одного

консистентного множества, содержащего эту пару, в частности, таковым не является νS (это множество

S-консистентно).

21.3.4. Решение: В качестве примера пары типов, связанных отношением νS, но не µS, можно взять

T, T для любого бесконечного типа T. Рассмотрим множество пар R T π , T π π 1, 2 .

Рассмотрев определение S, легко получаем R S R , и применение принципа коиндукции дает нам

R νS. Отсюда T, T νS, поскольку T, T R. С другой стороны, R µS, поскольку µS связывает

исключительно конечные типы — это можно установить, обозначив множество всех пар конечных типов

как R и получив µS R по принципу индукции.

Не существует пар конечных типов S, T , связанных отношением νS

, но не µS

, поскольку две

этих неподвижных точки совпадают. Это следует из того, что для любых S, T T

из S, T µS

следует S, T νS

. (Поскольку T представляет собой конечное дерево, последнее утверждение можно

получить индукцией по T. Нужно рассмотреть варианты, где T равен Top, T

, T

, использовать

определение S

и равенства S

νS

и S

µS

21.3.8. Решение: Сначала определим отношение тождества для древовидных типов: I T, T T

T . Если мы покажем, что I S-консистентно, то принцип коиндукции позволит нам заключить, что

I νS — то есть, что νS рефлексивно. Чтобы показать S-консистентность I, возьмем его элемент

T, T , и рассмотрим варианты его формы. Сначала допустим, что T Top. Тогда T, T Top, Top , а

эта пара принадлежит S I по его определению. Теперь допустим, что T T

. Тогда, поскольку

rev. 104

414

, T

I, с помощью определения S имеем T

, T

S I . Аналогично для T T

21.4.2. Решение: Согласно принципу коиндукции, достаточно показать, что множество U U F

T R

консистентно, т. е., U U F

T R

U U . Допустим, x, y U U . Возьмем любое z U . Тогда

x, z , z, y U U и, таким образом, по определению F

T R

, имеем x, y F

T R

U U .

21.5.2. Решение: Чтобы проверить инвертируемость, мы просто рассматриваем определения S

и S,

и убеждаемся, что каждое множество G

S,T

содержит не более одного элемента.

В определениях S

и S каждый вариант явням образом указывает форму поддерживаемого элемен-

та и состав его множества поддержки, так что нетрудно выписать support

и support

. (Сравните с

функцией поддержки для S

из Определения 21.8.4.)

21.5.4. Решение:

i a

b c

f g

21.5.6. Решение: Нет, путь от x νF µF необяхательно ведет к циклу в графе поддержки; он может

вести и к бесконечной цепочке. Рассмотрим, например, F ℘ N ℘ N , определяемую уравнением

F X 0 n n 1 X . Здесь µF 0 , а νF N. Кроме того, для всякого n νF µF , то есть,

для всякого n 0, support n n 1 , и таким образом порождается бесконечная цепочка.

21.5.13. Решение: Рассмотрим сначала частичную корректность. Доказательство в каждой части ве-

дется индукцией по рекурсивной структуре вызовов при прогоне алгоритма.

1. Из определения lfp нетрудно видеть, что эта функция возвращает значение истина в двух слу-

чаях. Если lfp X истина, потому что X , утверждение X µF тривиально верно. С

другой стороны, если lfp X истина потому, что support X истина, то, по предположению

индукции, support X µF , а отсюда Лемма 21.5.8 дает нам X µF .

2. Если gfp X ложь, потому что support X , то X µF по Лемме 21.5.8. В противном случае,

lfp X ложь потому, что lfp support X ложь, и по предположению индукции, support X

µF . По Лемме 21.5.8, X µF .

Затем нам нужно охарактеризовать порождающие функции F , для которых lfp гарантированно за-

вершается за конечное число шагов. Здесь будет полезно терминологическое нововведение. Если име-

ется порождающая функция F ℘ U ℘ U с конечным числом состояний, то частичная функция

height

U N (или просто height, «высота») будет наименьшая частичная функция, удовлетворяю-

щая следующему условию:

height x

0 если support x

1 max height y y support x если support x

(Обратите внимание, что height x не определена, если x либо участвует в цикле доступности, либо

зависит от элемента такого цикла.) Будем говорить, что порождающая функция F имеет конечную

высоту, если height

представляет собой тотальную функцию. Нетрудно проверить, что, если y

support x , и определены как height y , так и height x , то height y height x .

Теперь мы можем сказать, что если функция F имеет конечное число состояний и конечную вы-

соту, то lfp X завершается для всякого конечного входного множества X U . Чтобы убедиться в

этом, заметим, что, поскольку у F конечное число состояний, в каждом рекурсивном вызове lfp Y ,

происходящем от исходного вызова lfp X , множество Y конечно. Поскольку F имеет конечную высо-

ту, функция h Y max height y y Y правильно определена. Поскольку h Y уменьшается при

каждом рекурсивном вызове и всегда неотрицательна, она может служить мерой завершения для lfp.

21.8.5. Решение: Определение S

такое же, как у S

, но только последний вариант не содержит

условий T µX.T

и T Top. Чтобы убедиться в неинвертируемости S

, заметим, что множество

Заметим, что такой способ задания функции height легко переформулировать как наименьшую неподвижную точку

монотонной функции на отношениях, представляющих частичные функции.

rev. 104

415

µX.Top,Top

содержит два порождающих множества: Top, µY.Top и µX.Top, Top (сравните с тем, как

то же множество выглядит для функции S

Поскольку все варианты, кроме последнего, в определениях S

и S

совпадают, а последний вариант

представляет собой ограничение последнего варианта S

, включение νS

νS

очевидно. В другом

направлении включение νS

νS

можно доказать с помощью принципа коиндукции и следующей

леммы, устанавливающей, что множество νS

-консистентно.

Лемма A.0.17 Для всякой пары µ-типов S, T если S, T νS

, то S, T S

νS

Набросок доказательства: Индукция по k µ-height S . Такая индукция выражает неформальную

идею, что любой вывод S, T νS

можно перевести в более короткий вывод того же самого утвер-

ждения, и этот последний всегда будет одновременно выводом утверждения S, T νS

. Вследствие

ограничений на правило левой µ-свертки полученный в результате трансформации вывод будет об-

ладать свойством, что всякая последовательность применений µ-свертки начинается с последова-

тельности левых µ-сверток, за которыми следует последовательность правых µ-сверток.

21.9.2. Решение:

T T

S T

S X µX.T T

S µX.T

(Отметим интересный факт, что порождающая функция T D отличается от других функций, рассмот-

ренных нами в этой главе: она не обратима. Например, B A B B C поддерживается двумя множе-

ствами, B A B и B B C , при том что ни одно из них не является подмножеством другого.)

21.9.7. Решение: Все правила для BU такие же, как для T D из решения к Упражнению 21.9.2, за

исключением правила для типов, начинающихся с конструкции µ:

S T

X µX.T S T

21.11.1. Решение: Таких пар типов много. Тривиальным примером может служить µX.T и X µX.T T

почти для любого T. Более интересный пример — µX.Nat (Nat X) и µX.Nat X.

22.3.9. Решение: Вот основные правила алгоритмического порождения ограничений:

Γ x T

x : T

(CT-Var)

Γ, x:T

1 F

: T

2 F

C x dom Γ

λx:T

: T

2 F

(CT-Abs)

: T

1 F

: T

2 F

F X, F

: X

(CT-App)

Остальные правила устроены так же. Эквивалентность исходных правил и их алгоритмического пред-

ставления формулируется следующим образом:

1. Корректность : Если Γ

t : T

C, а переменные, упоминающиеся в Γ и t, не встречаются

в F , то Γ t : T

F F

2. Полнота : Если Γ t : T

C, то существует такая перестановка F имен переменных из X ,

что Γ

t : T C

Оба утверждения доказываются прямолинейной индукцией по деревьям вывода. Для случая терма-

применения в части 1 оказывается полезна следующая лемма:

Если типовые переменные, встречающиеся в Γ и t, не содержатся в F , а Γ

t : T

то типовые переменные, встречающиеся в T и C, не содержатся в F F .

rev. 104

416

Для соответствующего случая в части 2 использутеся лемма

Если Γ

t : T

C, то Γ

F,G

t : T

F ,G

C, где G — произвольная последовательность

имен переменных.

22.3.10. Решение: Если представлять множества ограничений как списки пар типов, алгоритм порож-

дения ограничений будет простым переводом на ML правил вывода из решения к Упражнению 22.3.9.

let rec recon ctx nextu var t = match t with

TmVar ( fi ,i ,_ ) ->

let tyT = g e t T yp e F ro m C o nt e x t fi ctx i in

(tyT , nextuvar , [])

| TmAbs ( fi , x , tyT1 , t2 ) ->

let ctx ’ = ad d b i n ding ctx x ( VarBin d ( tyT1 )) in

let ( tyT2 , nextuvar2 , const r2 ) = recon ctx ’ ne xtuvar t2 in

( TyArr ( tyT1 , tyT2 ), nextuvar2 , const r2 )

| TmApp ( fi , t1 , t2 ) ->

let ( tyT1 , nextuvar1 , const r1 ) = recon ctx ne xtuvar t1 in

let ( tyT2 , nextuvar2 , const r2 ) = recon ctx ne x t uvar1 t2 in

let NextUVa r (tyX , nextuvar ’) = nextuv a r2 () in

let newconstr = [( tyT1 , TyArr ( tyT2 , TyId ( tyX )))] in

(( TyId ( tyX )) , nextuvar ’ ,

List . concat [ newconstr ; co nstr1 ; co nstr2 ])

| TmZero ( fi ) -> ( TyNat , nextuvar , [])

| TmSucc ( fi , t1 ) ->

let ( tyT1 , nextuvar1 , const r1 ) = recon ctx ne xtuvar t1 in

( TyNat , nextuvar1 , ( tyT1 , TyNat ):: c onstr1 )

| TmPred ( fi , t1 ) ->

let ( tyT1 , nextuvar1 , const r1 ) = recon ctx ne xtuvar t1 in

( TyNat , nextuvar1 , ( tyT1 , TyNat ):: c onstr1 )

| Tm IsZero (fi , t1 ) ->

let ( tyT1 , nextuvar1 , const r1 ) = recon ctx ne xtuvar t1 in

( TyBool , nextuvar1 , (tyT1 , TyNat ):: cons tr1 )

| TmTrue ( fi ) -> ( TyBool , nextuvar , [])

| TmFalse ( fi ) -> ( TyBool , nextuvar , [])

| TmIf ( fi ,t1 , t2 , t3 ) ->

let ( tyT1 , nextuvar1 , const r1 ) = recon ctx ne xtuvar t1 in

let ( tyT2 , nextuvar2 , const r2 ) = recon ctx ne x t uvar1 t2 in

let ( tyT3 , nextuvar3 , const r3 ) = recon ctx ne x t uvar2 t3 in

let newconstr = [( tyT1 , TyBoo l ); ( tyT2 , tyT3 )] in

( tyT3 , nextuvar3 ,

List . concat [ newconstr ; co nstr1 ; co nstr2 ; constr3 ])

22.3.11. Решение: Правило порождения ограничений для выражений fix несложно построить на ос-

нове правила типизации T-Fix с Рис. 11.12.

Γ t

: T

1 X

X не встречается в X

, Γ и t

Γ fix t

: X

X X

(CT-Fix)

В этом правиле реконструируется (под именем T

) тип терма t

, проверяется, что T

имеет вид X X

для некоторой новой переменной X, и X объявляется типом выражения fix t

В свою очередь, правило порождения ограничений для выражений letrec можно пострить на основе

CT-Fix и определения letrec как производной формы.

22.4.3. Решение:

X Nat, Y X X X Nat, Y Nat Nat

Nat Nat X Y X Nat, Y Nat

X Y Y Z, Z U W X U W, Y U W, Z U W

Nat Nat Y не унифицируется

Y Nat Y не унифицируется

rev. 104

417

22.4.6. Решение: Основная структура данных, необходимая для этого упражнения — представление

подстановок. Ее можно устроить по-разному; простым решением будет воспользоваться типом данных

constr из Упражнения 22.3.10; подстановка тогда будет просто множеством ограничений, где все левые

части — переменные унификации. Если мы определим функцию substinty, проводящую подстановку

типа для одной типовой переменной

let substinty tyX tyT tyS =

let rec f tyS = match tyS with

TyArr ( tyS1 , tyS2 ) -> TyArr ( f tyS1 , f tyS2 )

| TyNat -> TyNat

| TyBool -> TyBool

| TyId ( s ) -> if s = tyX then tyT else TyId (s )

in f tyS

то применение к типу подстановки целиком можно представить так:

let applysubst constr tyT =

List . fol d _ left

( fun tyS ( TyId ( tyX ), tyC2 ) -> s ubstinty tyX tyC2 tyS )

tyT ( List . rev con str )

Кроме того, функция унификации должна уметь применять подстановку ко всем типам в некотором

множестве ограничений:

let s u b s t i n c o n s t r tyX tyT constr =

List . map

( fun ( tyS1 , tyS2 ) ->

( substi n t y tyX tyT tyS1 , substin t y tyX tyT tyS2 ))

co nstr

Помимо этого, нужна «проверка на вхождение», обнаруживающая циклические зависимости:

let occursi n tyX tyT =

let rec o tyT = match tyT with

TyArr ( tyT1 , tyT2 ) -> o tyT1 || o tyT2

| TyNat -> false

| TyBool -> false

| TyId ( s ) -> ( s= tyX )

in o tyT

Теперь функцию унификации можно записать как прямой перевод псевдокода, приведенного на

Рис. 22.2. Как обычно, она принимает в качестве дополнительных аргументов позицию в файле и

строку, которые нужно будет использовать при распечатке сообщений об ошибке, если унификация

окажется неудачной.

let unify fi ctx msg constr =

let rec u constr = match con str with

[] -> []

| (tyS , TyId ( tyX )) :: rest ->

if tyS = TyId ( tyX ) then u rest

else if occursi n tyX tyS then

error fi ( msg ^ " :␣ cir c ular ␣ c o n s traints " )

else

List . append ( u ( s u b s t i n c o ns t r tyX tyS rest ))

[( TyId ( tyX ), tyS )]

| ( TyId ( tyX ), tyT ) :: rest ->

if tyT = TyId ( tyX ) then u rest

else if occursi n tyX tyT then

error fi ( msg ^ " :␣ cir c ular ␣ c o n s traints " )

else

List . append ( u ( s u b s t i n c o ns t r tyX tyT rest ))

rev. 104

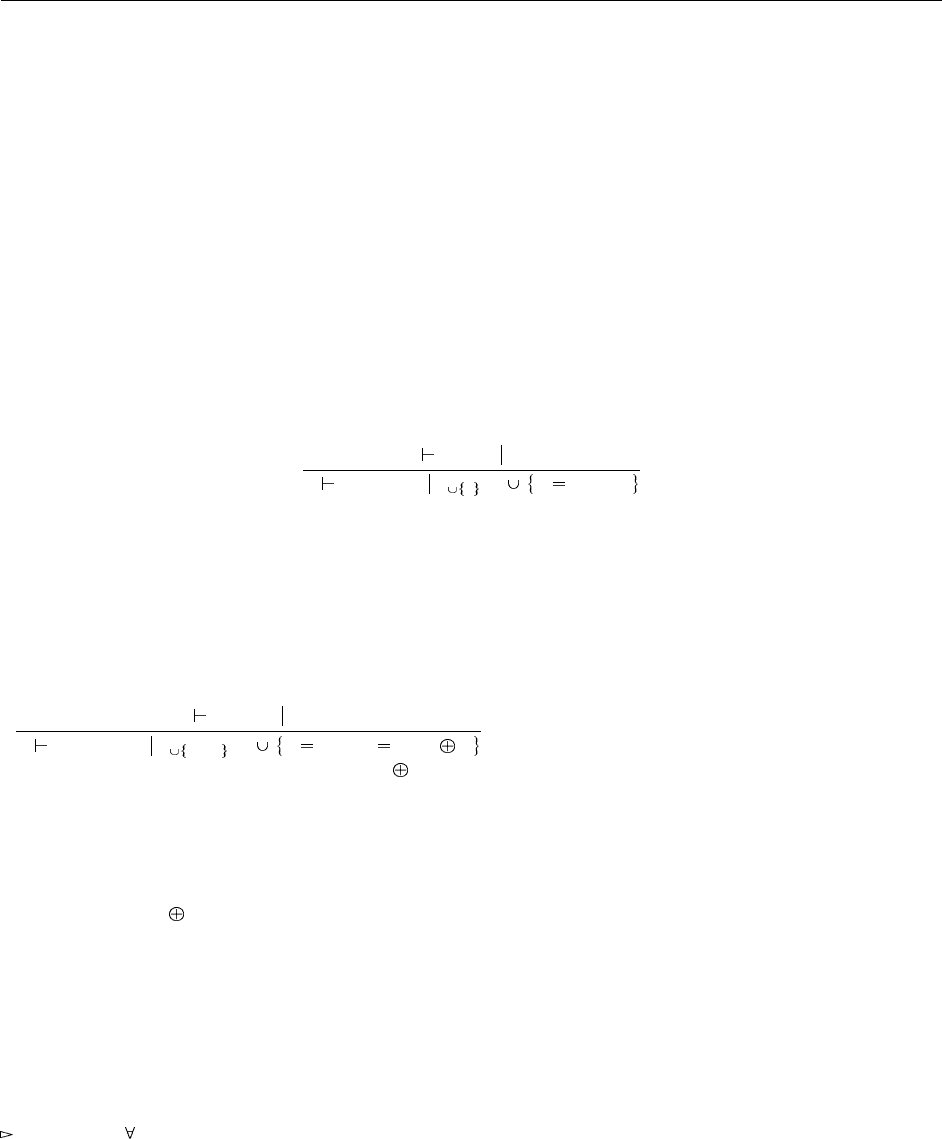
418

[( TyId ( tyX ), tyT )]

| ( TyNat , TyNat ) :: rest -> u rest

| ( TyBool , TyBool ) :: rest -> u rest

| ( TyArr ( tyS1 , tyS2 ), TyArr ( tyT1 , tyT2 )) :: rest ->

u (( tyS1 , tyT1 ) :: ( tyS2 , tyT2 ) :: rest )

| (tyS , tyT ):: rest ->

error fi " U n s o lvable ␣ c o n s t r a i n t s "

u constr

Эта педагогическая версия унификации не прилагает особенных усилий, чтобы сделать сообщения об

ошибке полезными и понятными. На практике «объяснение» ошибок типизации может быть одной из

самых сложных задач при разработке промышленного компилятора для языка с реконструкцией типов.

См. (Wand 1986).

22.5.6. Решение: Расширить алгоритм реконструкции типов на типы записей — непростая, хотя и ре-

шаемая задача. Основная сложность состоит в том, что неясно, какие ограничения требуется порождать

для проекции записи. Первая, наивная попытка может выглядеть как

Γ t : T

Γ t.l

: X

X X

C T {l

:X}

однако она оказывается неудовлетворительной, поскольку, в сущности, это правило говорит, что поле l

может получиться исключительно в результате проекции записи, содержащей только поле l

и больше

ничего.

Изящное решение было предложено Вандом (Wand 1987) и затем разработано Вандом (Wand 1988,

1989b), Реми (R´emy 1989, 1990) и другими. Мы воодим новую разновидность переменной, называемую

переменная строки. Значением такой переменной являются не типы, а «строки», состоящие из меток

полей и связанных с ними типов. С использованием переменных строк, правило порождения ограни-

чений для проекции поля можно записать как

Γ t

: T

Γ t

: X

X X,σ,ρ

C T {ρ}, ρ l

:X σ

(CT-Proj)

где σ и ρ — переменные строк, а операция склеивает две строки (при этом предполагается, что мно-

жества их меток полей не пересекаются). То есть, терм t.l

имеет тип X, если t имеет тип записей с

полями ρ, а ρ содержит поле l

:X и какие-то еще поля σ.

Ограничения, порождаемые при работе этого улучшенного алгоритма, имеют более сложный вид,

чем просто множество уравнений, содержащих переменные унификации, как получается при работе

исходного алгоритма, поскольку новые множества ограничений включают ассоциативную и коммута-

тивную операцию . Для нахождения решений таких множеств ограничений требуется простая разно-

видность эквациональной унификации.

23.4.3. Решение: Вот стандартное решение с использованием вспомогательной функции append:

ap pend = λX. ( fix (λapp :( List X) -> ( List X) -> ( List X ).

λl1 : List X. λl2 : List X.

if isnil [X] l1 then l2

else cons [X] ( head [X ] l1 )

( app ( tail [X ] l1 ) l2 )));

ap pend : X . List X -> List X -> List X

re verse =

λX .

( fix (λrev :( list X) -> ( List X ).

λl : ( List X ).

if isnil [X] l

then nil [ X]

else append [X ] ( rev ( tail [X] l ))

( cons [X ] ( head [X] l) ( nil [X ]))) );

rev. 104

419

re verse : X . List X -> List X

23.4.5. Решение:

and = λb : CBool . λc : CBool .

λX . λt:X. λf : X. b [ X] (c [X] t f) f;

23.4.6. Решение:

iszro = λn : CNat . n [ Bool ] (λb : Bool . false ) true ;

23.4.8. Решение:

pa irNat = λn1 : CNat . λn2 : CNat .

λX . λf: CNat -> CNat -> X . f n1 n2 ;

fs tNat = λp: Pai rNat . p [ CNat ] (λn1 : CNat . λn2 : CNat . n1 );

sn dNat = λp: Pai rNat . p [ CNat ] (λn1 : CNat . λn2 : CNat . n2 );

23.4.9. Решение:

zz = pairNat c

;

f = λp: PairNat . pair Nat ( sndNat p) ( cplus c

( sn dNat p ));

prd = λm : CNat . fstNat (m [ pa irNat ] f zz );

23.4.10. Решение:

vpred = λn : CNat . λX . λs :X ->X.

λz :X.

(n [( X- > X)-> X ]

(λp :(X ->X) - >X . λq :( X- > X). q ( p s ))

(λx :X ->X. z ))

(λx : X . x );

vpred : CNat -> CNat

Я благодарен Майклу Левину, который мне рассказал об этом примере.

23.4.11. Решение:

head = λX . λdefault :X. λl : List X.

l [X] (λhd :X . λtl :X. hd ) defau lt ;

23.4.12. Решение: Самое сложное в этом упражнении – функция вставки. Решение применяет данный

список l к функции, порождающей два новых списка, один из которых совпадает с исходным, а другой

включает e. Для каждого элемента hd в списке l (считая справа налево) в функцию передается сам hd

и пара списков, уже построенных для элементов справа от hd. Новая пара строится при сравнении e с

hd: если e меньше или равен, он должен находиться в начале получающегося списка; таким образом,

мы строим второй список результата, добавляя e к началу первого входного списка (того, где e не

содержится). С другой стороны, если e больше, чем hd, од должен находиться где-то в середине второго

списка, и новый список мы порождаем простым добавлением hd к уже полученному нами второму

списку.

in sert =

λX . λleq :X - >X -> Bool . λl : List X. λe : X.

let res =

l [ Pair ( List X) ( List X )]

(λhd : X. λacc : Pair ( List X) ( List X ).

let rest = fst [ List X] [ List X] acc in

let newre st = cons [X ] hd rest in

let restwithe = snd [ List X] [ List X] acc in

let n e w r e s t w i t h e =

if leq e hd

rev. 104

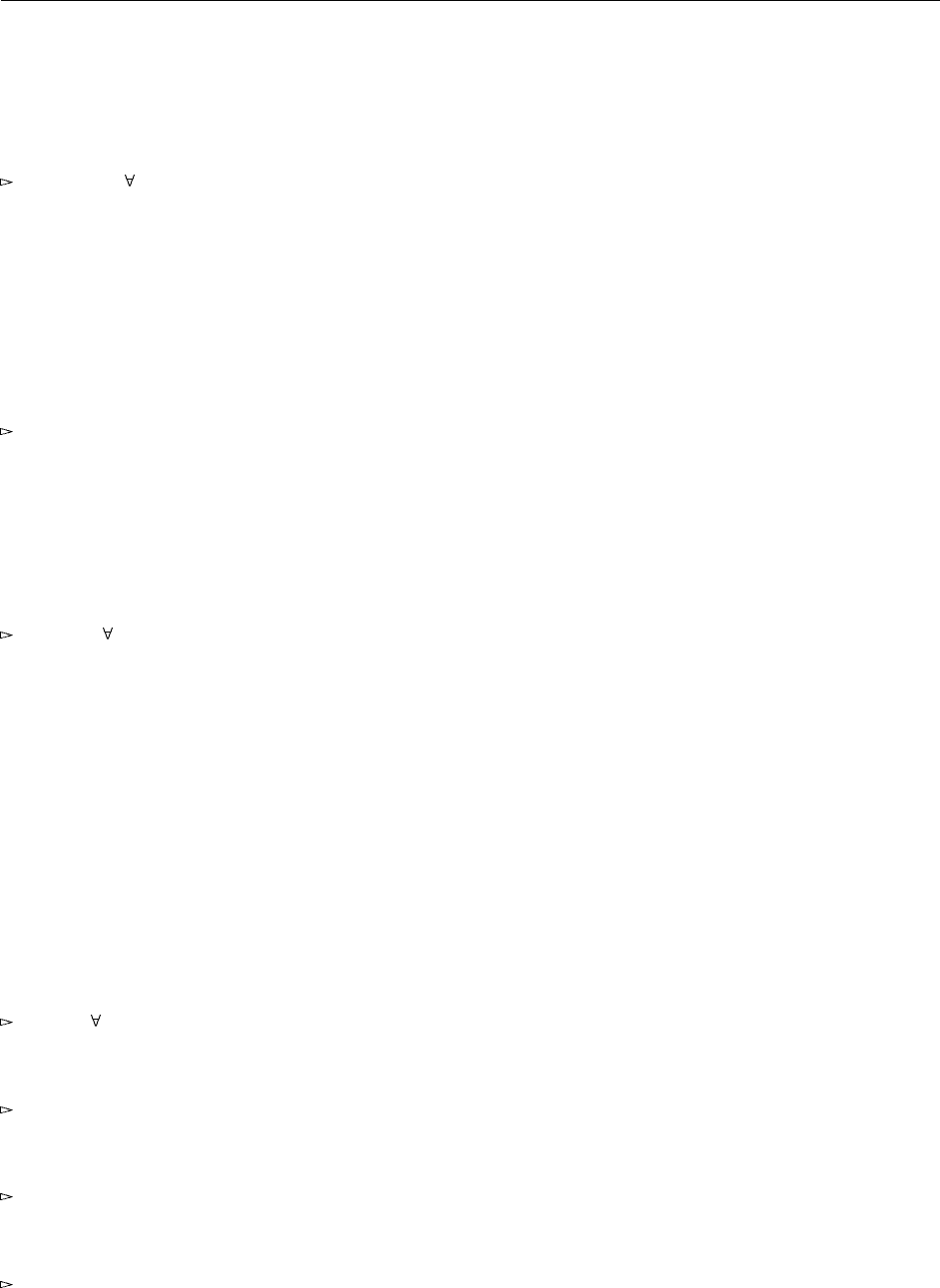
420

then cons [X] e ( cons [X] hd rest )

else cons [X] hd restw i the in

pair [ List X ] [ List X] ne wrest newrestwithe )

( Pair [ List X ] [ List X] ( nil [X ]) ( cons [X ] e ( nil [ X ])))

in snd [ List X] [ List X] res ;

in sert : X . (X ->X -> Bool ) -> List X -> X -> List X

Теперь нам нужна функция сравнения для чисел. Поскольку мы пользуемся числами-примитивами,

писать ее надо с помощью fix (Если бы мы использовали CNat вместо Nat, можно было бы обойтись

без fix).

le qnat =

fix (λf: Nat - >Nat - > Bool . λm : Nat . λn: Nat .

if isze ro m then true

else if iszero n then false

else f ( pred m ) ( pred n ));

le qnat : Nat -> Nat -> Bool

Наконец, мы строим функцию сортировки, по очереди вставляя каждый элемент исходного списка в

новый список:

sort = λX . λleq :X ->X -> Bool . λl : List X.

l [ List X]

(λhd : X λrest : List X. insert [ X ] leq rest hd )

( nil [X ]);

sort : X. (X - >X -> Bool ) -> List X -> List X

Чтобы убедиться, что сортировка работает, мы строим неупорядоченный список:

l = cons [ Nat ] 9

( cons [ Nat ] 2 ( cons [ Nat ] 6 ( cons [ Nat ] 4 ( nil [ Nat ]))));

сортируем его

l = sort [ Nat ] le qnat l;

и считываем содержимое:

nth =

λX . λde fault :X .

fix (λf :( List X) ->Nat - >X. λl: List X. λn: Nat .

if isze ro n

then head [X] de fault l

else f ( tail [ X] l ) ( pred n);

nth : X . X -> List X -> Nat -> X

nth [ Nat ] 0 l 0;

2 : Nat

nth [ Nat ] 0 l 1;

4 : Nat

nth [ Nat ] 0 l 2;

6 : Nat

nth [ Nat ] 0 l 3;

rev. 104