Пирс Б. Типы в языках программирования
Подождите немного. Документ загружается.

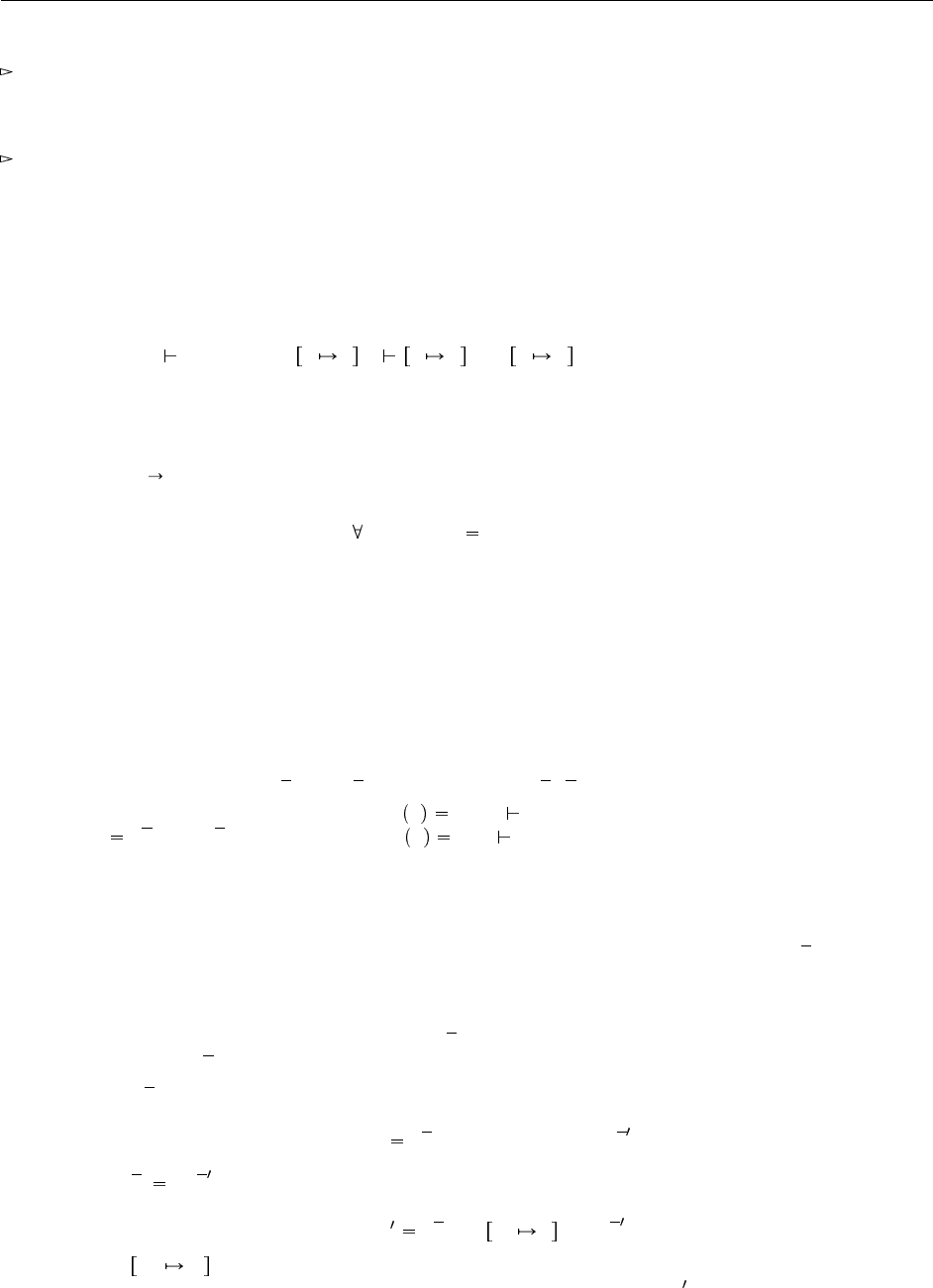
421
9 : Nat
nth [ Nat ] 0 l 4;
0 : Nat
Демонстрация, что на языке Системы F можно реализовать правильно типизированный алгоритм сор-
тировки, была достижением Рейнольдса (Reynolds 1985). Его алгоритм несколько отличался от пред-
ставленного здесь.
23.5.1. Решение: Структура доказательства почти такая же, как в 9.3.9 (см. стр. 9.3.9). Для правила
применения типа E-TappTabs требуется дополнительная лемма о подстановке, параллельная Лем-
ме 9.3.8 (см. стр. 9.3.8).
Если Γ, X, ∆ t : T, то Γ, X S ∆ X S t : X S T.
Дополнительный контекст ∆ здесь требуется, чтобы получить достаточное сильное предположение
индукции; если его опустить, сломается вариант T-Abs.
23.5.2. Решение: Опять же, структура доказательства очень похожа на доказательство свойства про-
движения для λ , Теорема 9.3.5. Лемма о канонических формах (9.3.4) расширяется одним дополни-
тельным вариантом
Если v является значением типа X.T
12
, то v λX.t
12
.
который используется в главном доказательстве в случае с применением типа.
23.6.3. Решение: Все части доказательства являются досвольно прямолинейными индуктивными и/и-
ли вычислительными рассуждениями, кроме самой последней, гле требуется немного больше изоб-
ретательности, чтобы увидеть, как соединить кусочки задачи и получить противоречие. Структура
рассуждения была предложена Павлом Ужичиным.
1. Прямолинейная индукция по t, с использованием леммы об обращении для типизации.
2. Индукцией по внешним абстракциям и применениям типов показываем, что
Если t имеет вид λ
Y. (r [B]) для некоторых Y, B и r (где от r не требуется быть
незащищенным), и при этом erase t m и Γ t : T, то имеется некоторый тип s вида
s λX. (u [A]), такой, что erase s m, Γ s : T, и вдобавок терм u незащищен).
В базовом случае нет никаких внешних абстракций и применений типа — т. е., r сам является
незащищенным, и требуемое условие выполняется.
В индуктивном случае внешний конструктор r либо абстракция типа, либо применение типа.
Если это применение типа, скажем, r
1
[R], мы добавляем R к последовательности B и применяем
предположение индукции. Если это абстракция типа, скажем, λZ. r
1
, нужно рассмотреть два
подварианта:
(a) Если последовательность применений B пуста, мы можем добавить Z к последовательности
абстракций Y и применить предположение индукции.
(b) Если B непуста, мы можем записать t в виде
t λY. ((λZ. r
1
) [B
0
] [B ])
где B B
0
B . Однако этот терм содержит редекс для правила R-Beta2; его сокращение
приводит нас к терму
t λY. (( B
0
Z r
1
) [B ])
где B
0
Z r
1
содержит строго меньше внешних абстракций и применений типов, чем r.
Более того, теорема о редукции субъекта говорит нам, что тип t совпадает с типом t. При-
менение предположения индукции ведет к требуемому результату.
rev. 104
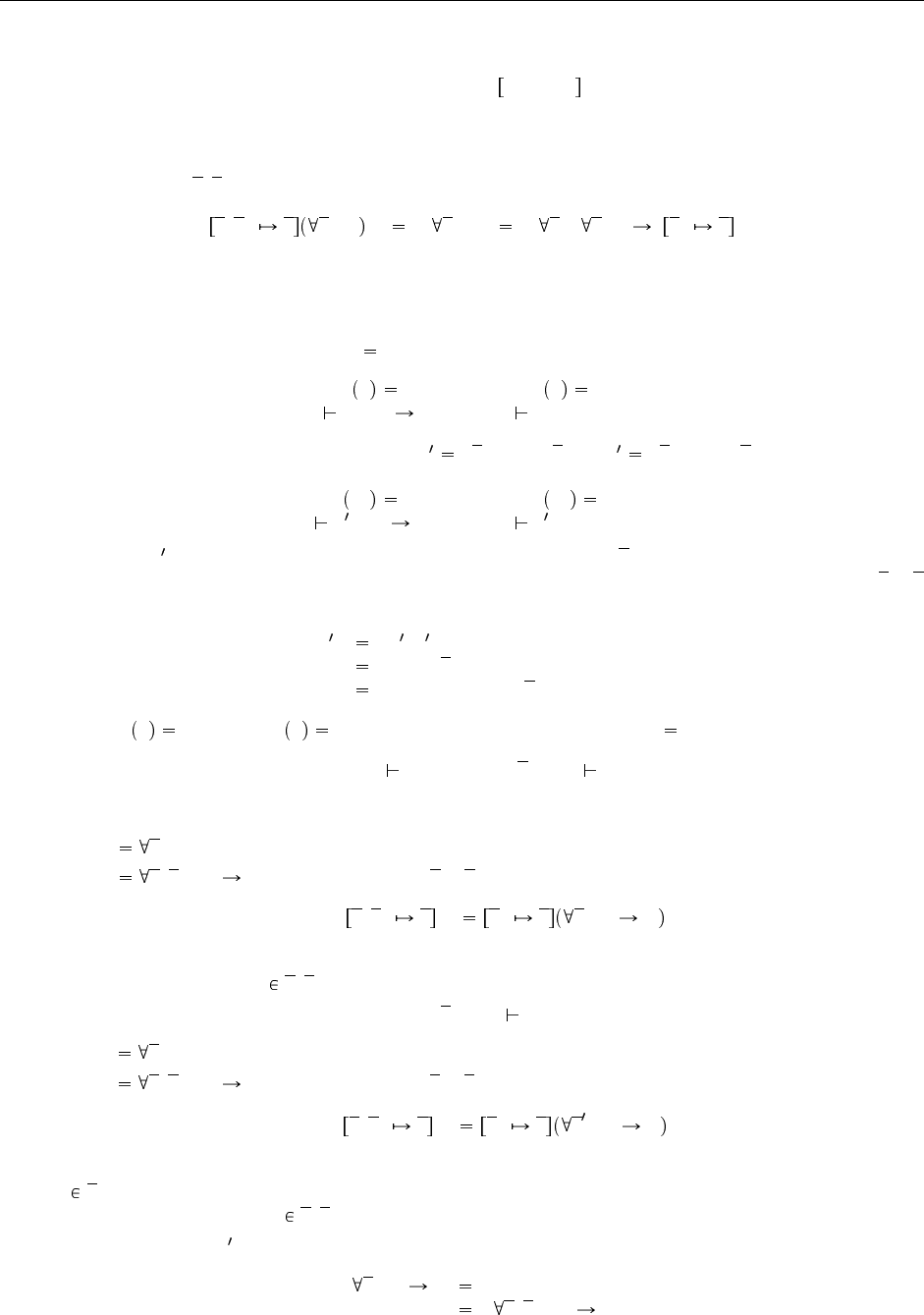
422
3. Непосредственно следует из леммы об обращении.
4. Прямолинейное вычисление из пунктов (1), (3) и дважды (2).
5. Непосредственно следует из пункта (2) и леммы об обращении.
6. Индукция по размеру T
1
. В базовом случае, когда T
1
— переменная, эта переменная должна
происходить из X
1
X
2
, поскольку в противном случае
X
1
X
2
A Y.T
1
Y.W Z.( Y.W) ( X
1
B T
2
)
а такого случиться не может (слева стрелок нет, а справа есть по крайней мера одна). Остальные
варианты непосредственно следуют из предположения индукции.
7. Предположим, что терм omega типизируем, и получим противоречие. Согласно пунктам (1) и (3),
существует незащищенный терм o s u, такой, что
erase s λx. x x erase u λy. y y
Γ s : U V Γ u : U.
Согласно пункту (2), существуют термы s λR. (s
0
[E]) и u λV. (u
0
[F]) с незащищенны-
ми s
0
и u
0
и
erase s
0
λx. x x erase u
0
λy. y y
Γ s : U V Γ u : U.
Поскольку s имеет функциональный тип, последовательность R должна быть пустой. Подобным
образом, поскольку s
0
и u
0
незащищенные, они должны начинаться с абстракций, так что E и F
также пусты, и мы имеем
o s u
s
0
(λV. u
0
)
(λx:T
x
. w) (λV. λy:T
y
. v),
где erase w x x и erase v y y. Согласно лемме об инверсии, U T
x
и
Γ, x:T
x
w : W Γ, V, y:T
y
v : P
Применяя пункт (4) к первому из этих утверждений, имеем либо
(a) T
x
X.X
i
, либо
(b) T
x
X
1
X
2
.T
1
T
2
, и для некоторых A и B
X
1
X
2
A T
1
X
1
B Z.T
1
T
2
.
По пункту (5), T
x
должен иметь вторую из этих форм, так что, по пункту (6), самым левым
листом типа T
1
будет X
i
X
1
X
2
.
Применяя теперь пункт (4) к типизации Γ, V, y:T
y
v : P, имеем либо
(a) T
y
Y.Y
i
, либо
(b) T
y
Y
1
Y
2
.S
1
S
2
, и для некоторых C и D
Y
1
Y
2
C S
1
Y
1
D Z .S
1
S
2
.
В первом из этих вариантов мы немедленно получаем, что самым левым листом типа T
y
является
Y
i
Y. Во втором случае мы можем воспользоваться пунктом (6) и, опять же, показать, что самым
левым листом T
y
будет Y
i
Y
1
Y
2
.
Однако из формы o и леммы об обращении мы получаем
V.T
y
V T
x
X
1
X
2
.T
1
T
2
,
rev. 104

423
так что, в частности, T
y
T
1
. Другими словами, самый левый лист типа T
1
совпадает с са-
мым левым листом T
y
. Таким образом, мы имеем T
x
X
1
X
2
.( Y.S) T
2
, причем одновременно
leftmost-leaf S X
i
X
1
X
2
и leftmost-leaf S Y
i
Y. Поскольку переменные X
1
X
2
и Y связыва-
ются в различных местах, мы вывели противоречие: наше исходное предположение, что omega
типизируем, должно быть ложным.
23.7.1. Решение:
let r = λX . ref (λx:X . x ) in
(r[ Nat ] := (λx: Nat . succ x);
(!( r[ Bool ])) true );
24.1.1. Решение: Пакет p предоставляет пользователю константу a и функцию f, но единственная
разрешенная типами этих компонент операция состоит в том, чтобы применить f к a сколько-то раз,
а затем выбросить результат. Пакет p7 позволяет пользователю создавать значения типа X, но ничего
сделать с этими значениями мы не можем. В пакете p8 обе компоненты можно использовать, но ничего
не спрятано — с тем же успехом мы можем просто отбросить упаковку.
24.2.1. Решение:
sta ckADT =
{* List Nat ,
{ new = nil [ Nat ],
push = λn : Nat . λs: List Nat . cons [ Nat ] n s ,
top = λs : List Nat . head [ Nat ] s ,
pop = λs : List Nat . tail [ Nat ] s ,
is empty = isnil [ Nat ]}}
as { Stack , { new : Stack , push : Nat - >Stack - > Stack , top : Stack - > Nat ,
pop : Stack - > Stack , isempt y : Stack - > Bool }};
sta ckADT : { Stack , { new : Stack , push : Nat - > Stack -> Stack , top : Stack -> Nat ,
pop : Stack - > Stack , isempt y : Stack - > Bool }}
let { Stack , stack } = sta c kADT in
stack . top ( stack . push 5 ( stack . push 3 stack . new ));
5 : Nat
24.2.2. Решение:
coun t e r A D T =
{* Ref Nat ,
{ new = λ_: Unit . ref 1,
get = λr : Ref Nat . !r ,
inc = λr : Ref Nat . r := succ (! r )}}
as { Counter ,
{ new : Unit -> Counter , get : Counter -> Nat , inc : Counter - > Unit }}
coun t e r A D T : { Counter ,
{ new : Unit -> Counter , get : Counter -> Nat ,
inc : Counter - > Unit }}
24.2.3. Решение:
Fli pFlop = { X , { state :X , methods : { read : X -> Bool , to ggle : X ->X ,
reset : X -> X }}};
f = {* Counter ,
{ state = zeroCounter ,
me thods = { read = λs: Counter . iseven ( sendget s),
to ggle = λs. Cou nter . sen dinc s ,
reset = λs : Co unter . zeroCounte r }}}
as FlipFlop ;
f : FlipFlop
rev. 104
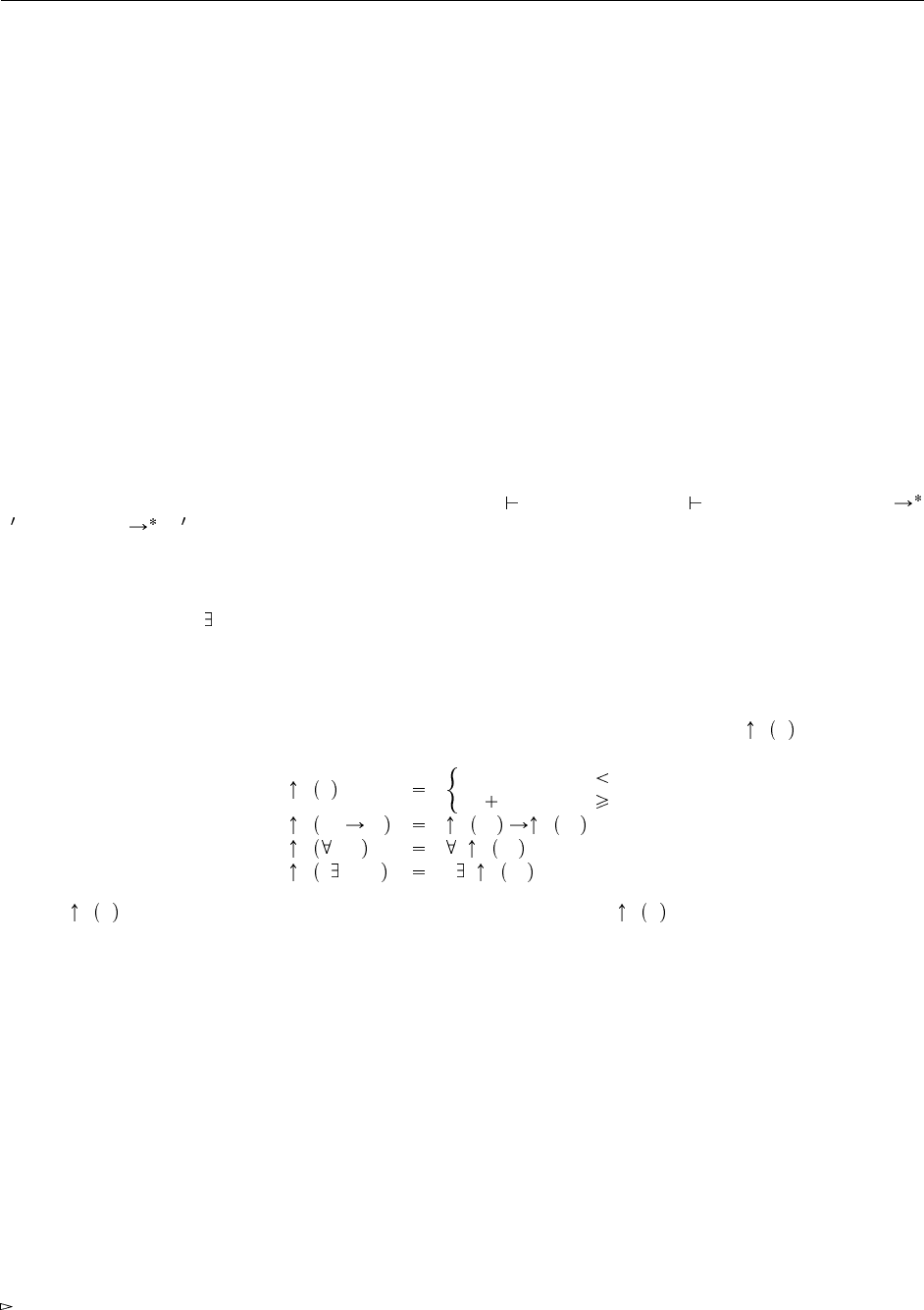
424
24.2.4. Решение:
c = {* Ref Nat ,
{ state = ref 5,
me thods = { get = λx: Ref Nat . !x ,
inc = λx : Ref Nat . (x := succ (! x ); x )}}}
as Counter ;
24.2.5. Решение: Такой тип позволит нам реализовать объекты-множества с методом union, но не
позволит их использовать. Чтобы вызвать метод union у такого объекта, нужно передать ему два
значения одного типа представления X. Однако эти значения не могут происходить из двух разных
объектов-множеств, поскольку, чтобы получить состояния обоих, нам пришлось бы их оба открыть,
и при этом оказались бы связаны две различных типовых переменных; состояние второго множества
нельзя было бы передать в операцию union первого. (Это не просто упрямство программы проверки ти-
пов: нетрудно заметить, что передавать конкретное представление одного множества в операцию union
другого было бы неправильно, поскольку представление второго множества может в общем случае как
угодно отличаться от представления первого.) Таким образом, эта версия типа NatSet позволяет нам
только вычислять объединение множества с самим собой!
24.3.2. Решение: По меньшей мере, требуется показать, что правила типизации и вычисления для
экзистенциальных типов сохраняются при переводе — т. е., если мы обозначим функцию, которая
проводит перевод, через J— K, нужно показать, что из Γ t : T следует JΓK JtK : JTK, и что из t
t следует JtK Jt K. Эти свойства легко поддаются проверке. Можно было бы также надеяться, что
верно обратное — что неверно типизированные термы языка, включающего экзистенциальные типы,
всегда переводятся в неверно типизированные термы, а тупиковые термы в тупиковые; к сожалению,
эти свойства не выполняются. Например, перевод отображает неверно типизированный (и тупиковый)
терм ({*Nat, 0} as { X,X}) [Bool] в правильно типизированный (и не тупиковый) терм.
24.3.3. Решение: Я не знаю, где бы такое преобразование было описано. Повидимому, оно должно быть
возможно, но трансформация не будет простым синтаксическим сахаром — ее придется применять ко
всей программе целиком.
25.2.1. Решение: Сдвиг типа T на d позиций при отсечении c, что записывается как
d
c
T , определяется
следующим образом:
d
c
k
k если k c
k d если k c
d
c
T
1
T
2
d
c
T
1
d
c
T
2
d
c
.T
1
.
d
c
T
1
d
c
{ ,T
1
} { ,
d
c
T
1
}
Запись
d
0
T обозначает сдвиг на d всех переменных в типе T, т. е.,
d
T .
25.4.1. Решение: Он освобождает место для типовой переменной X. Результат подстановки v
12
в терм t
2
должен быть правильно определен относительно контекста вида Γ, X, в то время как исходное значение
v
12
определено относительно просто Γ.
26.2.3. Решение: Одна из задач, где требуется правило полной F
<:
, — кодирование объектов по Абади,
Карделли и Вишванатану (Abadi, Cardelli and Viswanathan 1996), обсуждаемое также в (Abadi and
Cardelli 1996).
26.3.4. Решение:
sp luszz = λn: SZero . λm: SZero .
λX . λS <: X. λs :X ->S. λz : Z.
n [X] [S ] [ Z ] s ( m [ X ] [ S] [ Z] s z );
sp luspn = λn: SPos . λm: SNat .
λX . λS <: X. λs :X ->S. λz : Z.
n [X] [S ] [ X ] s ( m [ X ] [ S] [ Z] s z );
sp luspn : SPos -> Nat -> SPos
rev. 104
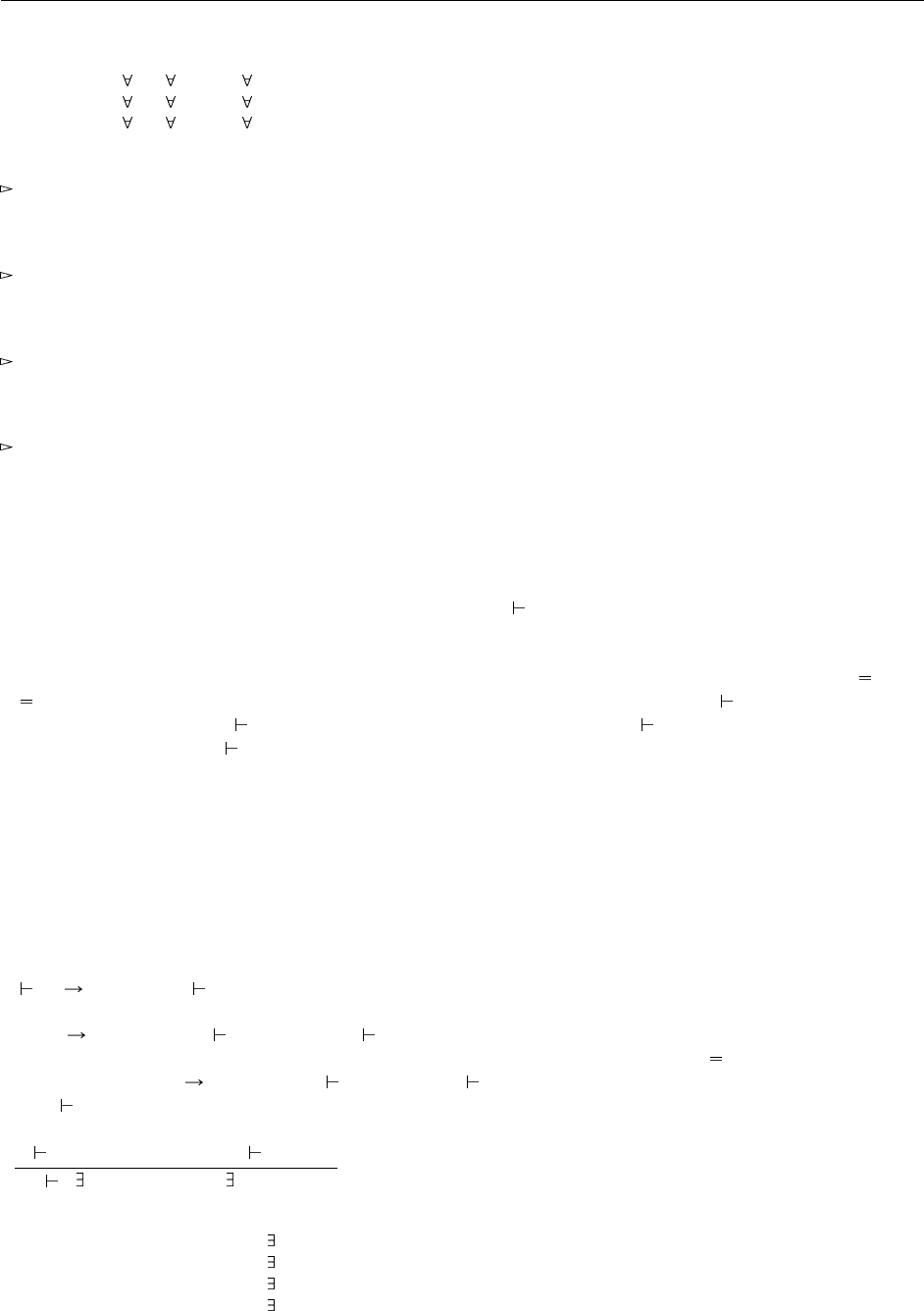
425
26.3.5. Решение:
SBool = X. T <: X. F <: X. T ->F ->X;
STrue = X. T <: X. F <: X. T ->F ->T;
SF alse = X . T <: X. F <: X. T ->F -> F ;
tru = λX . λT <: X. λF <: X . λt:T . λf :F . t ;
tru : STrue
fls = λX . λT <: X. λF <: X . λt:T . λf :F . f ;
fls : SFa lse
notft = λb : S False . λX. λT <: X . λF <: X. λt: T . λf:F . b [ X][ F ][ T ] f t ;
notft : SFa lse -> STrue
nottf = λb : STrue . λX . λT <: X. λF <: X . λt:T. λf : F. b[X ][ F ][ T] f t ;
notft : STrue -> S False
26.4.3. Решение: В вариантах с абстракцией и абстракцией типа в частях (1) и (2), а также в варианте
с квантором в частях (3) и (4).
26.4.5. Решение: В части (1) проводится индукция по деревьям вывода наследования. Все вариан-
ты получаются либо непосредственно (S-Refl, S-Top), либо несложным применением предположения
индукции (S-Trans, S-Arrow, S-All), за исключением S-TVar, где дела обстоят более интересно.
Предположим, последнее правило при выводе Γ, X<:Q, ∆ S <: T — экземпляр правила S-TVar, т. е.,
S представляет соой некую переменную Y, а T является верхней границей для этой переменной в кон-
тексте. Нужно рассмотреть два случая. Если X и Y — различные переменные, то предположение Y<:T
имеется также в контексте Γ, X<:P, ∆, и тогда результат следует непосредственно. Если же X Y, то
T Q; чтобы завершить доказательство, мы должны показать, что Γ, X<:P, ∆ X <: Q. По правилу
S-TVar имеем Γ, X<:P, ∆ X <: P. Более того, по предположению, Γ P <: Q, и по лемме об ослаб-
лении (26.4.2, Γ, X<:P, ∆ P <: Q. Склеивание двух этих выводов через S-Trans дает нам требуемый
результат.
Часть (2) представляет собой несложную индукцию по деревьям вывода типов, с использованием
части (1) для предпосылки о наследовании в варианте с применением типа.
26.4.11. Решение: Все доказательства представляют собой прямолинейные индукции по деревьям вы-
вода наследования. Мы приводим только первое из них, рассматривая варианты последнего правила
в выводе. Варианты S-Refl и S-Top следуют непосредственно. S-TVar возникнуть не может (ле-
вая сторона заключения S-TVar всегда переменная, а не функциональный тип); точно так же невоз-
можно правило S-All. Если последнее правило — экземпляр S-Arrow, поддеревья дают требуемые
результаты. Наконец, предположим, что последнее правило — экземпляр S-Trans — т. е., мы имеем
Γ S
1
S
2
<: U и Γ U <: T для некоторого U. По предположению индукции, либо U равен Top (тогда
T тоже равен Top по пункту (4) данного упражнения, и требуемый результат получен), либо U имеет
вид U
1
U
2
, причем Γ U
1
<: S
1
и Γ S
2
<: U
2
. Во втором случае мы применяем предположение
индукции ко второму подвыводу исходного S-Trans и получаем, что либо S Top (и все доказано),
либо T имеет вид T
1
T
2
, причем Γ T
1
<: U
1
и Γ U
2
<: T
2
. Два применения транзитивности дают
нам Γ T
1
<: S
1
и S
2
<: T
2
, откуда требуемый результат следует по правилу S-Arrow.
26.5.1. Решение:
Γ S
1
<: T
1
Γ, X<:S
1
S
2
: T
2
Γ { X<:S
1
,S
2
} <: { X<:T
1
,T
2
}
S-Some
26.5.2. Решение: Без наследования имеется всего четыре типа:
{* Nat , {a =5 , b =7}} as { X , {a: Nat ,b : Nat }};
{* Nat , {a =5 , b =7}} as { X , {a:X ,b: Nat }};
{* Nat , {a =5 , b =7}} as { X , {a: Nat ,b : X }};
{* Nat , {a =5 , b =7}} as { X , {a:X ,b:X }};
rev. 104

426
С наследованием и ограниченной квантификацией добавляется множество других — к примеру,
{* Nat , {a =5 , b =7}} as { X , {a: Nat }};
{* Nat , {a =5 , b =7}} as { X , {b: X }};
{* Nat , {a =5 , b =7}} as { X , {a: Top ,b : X }};
{* Nat , {a =5 , b =7}} as { X , Top };
{* Nat , {a =5 , b =7}} as { X <: Nat , {a:X ,b :X }};
{* Nat , {a =5 , b =7}} as { X <: Nat , {a: Top , b:X }};
26.5.3. Решение: Один из способов достичь желаемого — вложить АТД счетчика со сбросом внутрь
АТД обычного счетчика:
coun t e r A D T =
{* Nat ,
{ new = 1, get = λi: Nat . i , inc = λi : Nat . succ ( i ),
rcADT =
{* Nat ,
{ new = 1, get = λi: Nat . i inc = λi : Nat . succ ( i ),
reset = λi : Nat . 1}}
as { Res etCounter <: Nat ,
{ new : Re setCounter , get : Reset Counter - > Nat ,
inc : ResetCounter -> ResetCoun ter ,
reset : ResetCoun ter -> R e s e t C o u n t e r }} }}
as { Counter ,
{ new : Counter , get : Counter - >Nat , inc : Counter - > Counter ,
rcADT :
{ ResetCounter <: Counter ,
{ new : Re setCounter , get : Reset Counter - > Nat ,
inc : ResetCounter -> ResetCoun ter ,
reset : ResetCoun ter -> R e s e t C o u n t e r }}}};
coun t e r A D T : { Counter ,
{ new : Counter , get : Counter - >Nat , inc : Counter -> Counter ,
rcADT :{ R esetC ounter <: Counter ,
{ new : ResetCounter , get : ResetCounter -> Nat ,
inc : Reset Counter - > ResetCounter ,
reset : ResetCounte r - > ResetCounter }}}}
Когда эти пакеты открываются, получается, что контекст, в котором происходит проверка ти-
пов для оставшейстя части программы, содержит связывания вида Counter<:Top, counter:{...},
ResetCouner<:Counter, resetCounter:{...}:
let { Counter , cou nter } = counte r A D T in
let { ResetCounter , resetCounter } = counter . rcADT in
co unter . get
( cou nter . inc
( resetCounter . reset ( resetCounter . inc r e s e t C o u n t e r . new )));
2 : Nat
26.5.4. Решение: Требуется только добавить границы в очевидные места в кодирование по §24.3. На
уровне типов получаем:
X : S, T
def
Y. ( X<:S. T Y) Y
Изменения на уровне термов отсюда прямо следуют.
27.0.1. Решение: Вот один из способов:
setCounterClas s =
λM <: SetCount e r . λR <: C ounterRep .
λself : Ref (R - >M ).
λr : R .
{ get = λ_: Unit . !( r.x ) ,
rev. 104
427
set = λi : Nat . r.x := i,
inc = λ_ : Unit . (! self r). set ( succ ((! self r ). get unit ))};
setCounterClas s : M <: S e tCounter .
R <: Coun t e r R ep .
( Ref (R -> M )) -> R -> SetCounter
instrCoun t e r C l as s =
λM <: InstrCounter .
λR <: InstrCou n t e r R e p .
λself : Ref (R - >M ).
λr : R .
let super = se tC O u n t e r Cl a s s [ M] [ R] self in
{ get = ( super r ). get ,
set = λi : Nat . (r. a := succ (!( r.a )); ( super r ). set i ),
inc = ( super r ). inc ,
acc esses = λ_: Unit . !( r.a )};
instrCoun t e r C l as s : M <: InstrCounter .
R <: InstrCounter R e p .
( Ref (R -> M )) -> R -> InstrCounter
newInstrCounte r =
let m = ref (λr : InstrCounterRe p . error as InstrCounter ) in
let m ’ =
instrCoun t e r C l as s [ InstrCounter ] [ Inst r C o u n t e rR e p ] m in
(m := m ’;
λ_ : Unit . let r = {x= ref 1 a = ref 0} in m ’ r );
newInstrCounte r : Unit -> In s t r C o u n t e r
28.2.3. Решение: В варианте T-TAbs требуется тривиальным образом использовать S-Refl, что-
бы снабдить правило S-All дополнительной предпосылкой. В варианте T-TApp лемма об обраще-
нии наследования (для полной F
<:
) говорит нам, что N
1
X<:N
11
.N
12
, причем Γ T
11
<: N
11
и Γ, X<:T
11
N
12
<: T
12
. Благодаря транзитивности, имеем Γ T
2
<: T
11
, и поэтому мы имеем
право применить TA-TApp и получить Γ t
1
[T
2
] : X T
2
N
2
. Завершаем доказательство, как
и раньше, с помощью леммы о сохранении наследования при подстановке (Лемма 26.4.8) получая
Γ X T
2
N
12
<: X T
2
T
12
T.
28.5.1. Решение: Для полной F
<:
неверна Теорема 28.3.5 (а именно, вариант с правилом S-All).
28.5.6. Решение: Прежде всего заметим, что нельзя позволять ограниченным и неограниченным кван-
торам смешиваться: должно быть правило наследования для сравнения двух ограниченных кванторов,
и отдельное правило для сравнения двух неограниченных кванторов. Иначе мы снова окажемся в том
положении, с которого начинали!
Что касается частей (1) и (2), подробности можно найти у Катияра и Санкара (Katiyar and Sankar
1992). В части (3) ответ отрицательный: при добавлении типов-записей с наследованием в ширину систе-
ма снова оказывается неразрешимой. Проблема в том, что пустой тип записей играет роль своего рода
максимального типа (для записей), и с его помощью можно заставить программу проверки типов за-
циклиться, используя модифицированную версию примера Гелли. Если T X<:{}. {a: Y<:X. Y},
то при подаче на вход X
0
<:{a:T} X
0
<: {a: X
1
<:X
0
. X
1
} проверка типов никогда не закончится.
При подготовке этого примера мне помог Мартин Хофман. То же самое наблюдение высказано в
(Katiyar and Sankar 1992).
28.6.3. Решение:
1. Я вижу 9 общих подтипов:
X<:Y’ Z.Y Z’ X<:Y’ Z.Top Z’ X<:Y’ Z.X
X<:Y’ Top.Y Z’ X<:Y’ Top.Top Z’ X<:Y’ Top.X
X<:Top.Y Z’ X<:Top.Top Z’ X<:Top.X
rev. 104

428
R Y<:S.T
Y<:S. R T
если X F V S
Top
если X F V S
R { Y<:S,T}
{ Y<:S, R T }
если X F V S
Top
если X F V S
R S T
L S R T
если L S неудача
Top
если L S неудача
R X T, когда X<:T Γ
R Y Y, когда Y X
R Top Top
L Y<:S.T
Y<:S. L T
если L T неудача
и X F V S
неудача
иначе
L { Y<:S,T}
{ Y<:S, L T }
если L T неудача
и X F V S
неудача
иначе
L S T
R S L T
если L T неудача
неудача
если L T неудача
L X неудача
L Y Y, когда Y X
L Top Top
Рис. A.2. Наименьший надтип и наибольший подтип данного типа, не содержащие X
2. Типы X<:Y’ Z.Y Z’ и X<:Y’ Z.X оба являются нижними гранями для S и T, но у них нет
общего надтипа, который был бы при этом подтипом S и T.
3. Рассмотрите S Top и T Top. (Или X<:Y’ Z. Y Z’ и X<:Y’ Z. X.)
28.7.1. Решение: Функции R
X,Γ
и L
X,Γ
, переводящие соответственно каждый тип в его наименьший
надтип, не содержащий X, и в наибольший подтип, не содержащий X, определены на Рис. A.2. (Чтобы
облегчить чтение, мы опускаем индексы X и Γ.) У этих двух определений различные дополнительные
условия, поскольку, когда требуется вычислить L, нужно проверять, определена ли она (что записы-
вается L T неудача); R же определена всегда, поскольку в системе имеется тип Top. Правильность
этих определений доказывается в (Ghelli and Pierce 1998).
28.7.2. Решение: Простой способ показать неразрешимость полных ограниченных экзистенциальных
типов (Гелли и Пирс, Ghelli and Pierce 1998) — определить функцию перевода J—K, отображающую
задачи проверки наследования в полной F
<:
в задачи проверки наследования в системе, содержащей
только экзистенциальные типы, так что Γ S <: T доказуемо в F
<:
тогда и только тогда, когда в
системе с экзистенциальными типами доказуемо JΓ S <: TK. Такое кодирование на типах можно
определить уравнениями
JXK X JTopK Top
J X<:T
1
.T
2
{ X<:T
1
, JT
2
K} JT
1
T
2
K JT
1
K JT
2
K
где S X<:S.X. Мы очевидным образом распространяем его на контексты: JX
1
<:T
1
, . . . , X
n
<:T
n
K
X
1
:JT
1
K, . . . , X
n
:JT
n
K и на утверждения о наследовании: JΓ S <: TK JΓK JSK<:JTK.
29.1.1. Решение: X.X X — простой тип; его элементом будет, например, λX.λx:X.x. Такие термы
являются полиморфными функциями, которые, будучи конкретизированы типом T, дают функцию из
T в T. Напротив, λX.X X — оператор над типами — функция, которая, будучи применена к типу T,
выдает простой тип T T функций из T в T.
Другими словами, X.X X — тип, чьими элементами являются функции на уровне термов, пе-
реводящие типы в термы; конкретизация такой функции (для этого надо применить ее к типу, что
записывается t [T]) дает нам элемент функционального типа T T. С другой стороны, λX.X X сам
по себе является функцией (из типов в типы); его конкретизация типом T (что записывается (λX.X X)
T) дает сам тип T T, а не один из его элементов.
rev. 104
429
Например, если fn имеет тип X.X X, а Op λX.X X, то fn [T] : T T Op T.
29.1.2. Решение: Nat Nat представляет собой (простой) тип функций, а не функцию на уровне типов.
30.3.3. Решение: Лемма 30.3.1 используется в вариантах T-Abs, T-TApp и T-Eq. Лемма 30.3.2 ис-
пользуется в варианте T-Var.
30.3.8. Решение: Индукция по сумме размеров данных выводов, с разбором вариантов последних
правил в обоих из них. Если какой-то из выводов заканчивается на QR-Refl, то второй является
требуемым результатом. Если какой-то из выводов заканчивается на QR-Abs, QR-Arrow или QR-
All, то, исходя из формы этих правил, оба вывода должны заканчиваться одинаковыми правилами, и
результат получается простым применением предположения индукции. Если оба вывода заканчиваются
на QR-App, результат, опять же, несложным образом следует из предположения индукции. Оставшиеся
случаи более интересны.
Если оба вывода заканчиваются на QR-AppAbs, то мы имеем
S (λX::K
11
.S
12
) S
2
T X T
2
T
12
U X U
2
U
12
,
причем
S
12
V T
12
S
2
V T
2
S
12
V U
12
S
2
V U
2
.
Согласно предположению индукции, существуют такие типы V
12
и V
2
, что
T
12
V V
12
T
2
V V
2
U
12
V V
12
U
2
V U
2
.
Два раза применяя Лемму 30.3.7, получаем X T
2
T
12
V X V
2
V
12
и X U
2
U
12
V X V
2
V
12
—
то есть, T V V и U V V.
Допустим, наконец, один из выводов (скажем, первый) заканчивается на QR-App, а другой на
QR-AppAbs. В этом случае имеем
S (λX::K
11
.S
12
) S
2
T (λX’::K
11
.T
12
) T
2
U X U
2
U
12
,
где снова S
12
V T
12
, S
2
V T
2
, S
12
V U
12
и S
2
V U
2
. Снова, согласно предположению индукции, имеются
типы V
12
и V
2
, такие, что T
12
V V
12
, T
2
V V
2
, U
12
V V
12
и U
2
V U
2
. Применение правила QR-AppAbs
к первому и второму из этих утверждений, а Леммы 30.3.7 к третьему и четвертому дает нам T V V и
U V V.
30.3.10. Решение: Прежде всего мы замечаем, что любой вывод утверждения S WV T можно пе-
рестроить так, чтобы ни симметрия, ни транзитивность не использовалась в подвыводах экземпляров
правила симметрии — то есть, мы можем перейти от S к T через последовательность шагов, склеенных
QR-Trans, где каждый шаг состоит из одношаговой редукции, за которой, возможно, следует одно
применение правила симметрии. Эту последовательность можно изобразить так.
x
=
&
=
=
=
=
=
=
=
=
=
=
=
=
y
;
%
;
;
;
;
;
;
;
;
;
;
;
;
y
T
S
=
&
=
=
=
=
=
=
=
=
=
=
=
=
x
(стрелки, направленные справа налево, изображают редукции, заканчивающиеся применением сим-
метрии, а стрелки слева направо — редукции без симметрии). Теперь мы можем в цикле при помощи
Леммы 30.3.8 добавлять снизу диаграммы маленькие ромбы, пока не доберемся до общего результата
rev. 104

430
редукции S и T.
x
=
&
=
=
=
=
=
=
=
=
=
=
=
=
y
;
%
;
;
;
;
;
;
;
;
;
;
;
;
y
;
%
T
x
S
=
&
=
=
=
=
=
=
=
=
=
=
=
=
x
<
&
x
<
&
x
=
&
x
=
&
x
=
&
x
То же самое рассуждение можно представить и в стандартной индуктивной форме, без использования
картинок, но это только сделает его сложнее для понимания, не добавляя убедительности.
30.3.17. Решение: При добавлении первого странного правила сломается свойство продвижения; свой-
ство сохранения останется верным. Второе правило сломает как продвижение, так и сохранение.
30.3.20. Решение: Сравните свое решение с исходными текстами интерпретатора fomega.
30.5.1. Решение: Вместо семейства типов FloatList n у нас будет параметрическое семейство типов
List T n со следующими операциями:
nil : X . List X 0
cons : X . Πn: Nat . X -> List X ( succ n)
hd : X. Πn : Nat . List X ( succ n) -> X
tl : X. Πn : Nat . List X ( succ n) -> List X n
31.2.1. Решение:
Γ A <: Id B Да
Γ Id A <: B Да
Γ λX.X <: λX.Top Да
Γ λX. Y<X. Y <: λX. Y<Top. Y Нет
Γ λX. Y<X. Y <: λX. Y<X. X Да
Γ F B <: B Да
Γ B <: F B Нет
Γ F B <: F B Да
Γ F<:(λY.Top Y). F A <: F<:(λY.Top Y). Top B Да
Γ F<:(λY.Top Y). F A <: F<:(λY.Top Y). F B Нет
Γ Top[* *] <: Top[* * *] Нет
32.5.1. Решение: Главное, что требуется заметить — Object M является экзистенциальным типом:
Object служит сокращением для оператора
λM ::* *. { X , { state :X , methods :M X }}
Когда мы применяем этот оператор к M, получается редекс, сводящийся к экзистенциальному типу
{ X , { state :X , method s : M X }}
Заметим, что в этом преобразовании никак не используется включение — и следовательно, нет никакой
потери информации.
32.5.2. Решение:
se ndget =
λM <: Coun terM . λo : O bject M .
let {X , b } = o in b. method s . get (b . state );
sen d r eset =
rev. 104
