Пирс Б. Типы в языках программирования
Подождите немного. Документ загружается.


401
Остальные варианты:
Остальные сочетания (S-Arrow/S-Rcd и S-Rcd/S-Arrow) возникнуть не могут, поскольку при этом
на форму U накладываются противоречивые требования.
16.1.3. Решение: Если мы добавляем тип Bool, первая часть Леммы 16.1.2 требует небольшой моди-
фикации. Она должна гласить: «S <: S можно вывести без использования S-Refl для любого типа S,
кроме Bool ». Второй вариант — добавить правило
Bool <: Bool
в определение отношения наследования, и затем показать, что S-Refl можно исключить из обогащен-
ной системы.
16.2.5. Решение: Индукция по деревьям декларативного вывода типов. Рассмотрим варианты послед-
него правила в дереве.
Вариант T-Var: t x Γ x T
Утверждение следует непосредственно, по правилу TA-Var.
Вариант T-Abs: t λx:T
1
.t
2
Γ, x:T
1
t
2
: T
2
T T
1
T
2
По предположению индукции, Γ, x:T
1
t
2
: S
2
для некоторого S
2
<: T
2
. Согласно TA-Abs, Γ
t : T
1
S
2
. По правилу S-Arrow, T
1
S
2
<: T
1
T
2
, как нам и требуется.
Вариант T-App: t t
1
t
2
Γ t
1
: T
11
T
12
Γ t
2
: T
11
T T
12
По предположению индукции, Γ t
1
: S
1
для некоторого S
1
<: T
11
T
12
, и Γ t
2
: S
2
для некото-
рого S
2
<: T
11
. Согласно лемме об обращении отношения наследования (15.3.2), тип S
1
должен иметь
вид S
11
S
12
для некоторых S
11
и S
12
, причем T
11
<: S
11
и S
12
<: T
12
. По транзитивности наследова-
ния, S
1
<: S
11
. Из полноты алгоритмического отношения наследования следует S
1
<: S
11
. Теперь
применяем TA-App и получаем Γ t
1
t
2
: S
12
, что завершает рассмотрение данного варианта (по-
скольку мы уже имеем S
12
<: T
12
).
Вариант T-Rcd: t {l
i
=t
i
i 1..n
} Γ t
i
: T
i
для каждого i
T {l
i
:T
i
i 1..n
}
Не представляет труда.
Вариант T-Proj: t t
1
.l
j
Γ t
1
: {l
i
:T
i
i 1..n
} T T
j
Доказательство подобно варианту с термом-применением.
Вариант T-Sub: t : S S <: T
Утверждение следует из предположения индукции и транзитивности наследования.
16.2.6. Решение: Терм λx:{a:Nat}.x имеет, согласно декларативным правилам, типы
{a:Nat} {a:Nat} и {a:Nat} Top. Однако без правила S-Arrow эти типы оказываются несрав-
нимы (и не имеется типа, лежащего ниже их обоих).
16.3.2. Решение: Для начала мы приводим пару взаимно рекурсивных алгоритмов, которые, как мы
утверждаем (и намереваемся доказать), вычисляют, соответственно, объединение J и пересечение M па-
ры типов S и T. Второй из алгоритмов может также вернуть значение неудача, что означает отсутствие
у S и T пересечения.
rev. 104

402
S T =
Bool если S T Bool
M
1
J
2
если S S
1
S
2
T T
1
T
2
S
1
T
1
M
1
S
2
T
2
J
2
{j
l
:J
l
l 1..q
} если S {k
j
:S
j
j 1..m
}
T {l
i
:T
i
i 1..n
}
j
l
l 1..q
k
j
j 1..m
l
i
i 1..n
S
j
T
i
J
l
для каждого j
l
k
j
l
i
Top в остальных случаях
S T =
S если T Top
T если S Top
Bool если S T Bool
J
1
M
2
если S S
1
S
2
T T
1
T
2
S
1
T
1
J
1
S
2
T
2
M
2
{m
l
:M
l
l 1..q
} если S {k
j
:S
j
j 1..m
}
T {l
i
:T
i
i 1..n
}
m
l
l 1..q
k
j
j 1..m
l
i
i 1..n
S
j
T
i
M
l
для каждого m
l
k
j
l
i
M
l
S
j
если m
l
k
j
вcтречается только в S
M
l
T
i
если m
l
l
i
вcтречается только в T
неудача в остальных случаях
В случае функционального типа в первом алгоритме вызов второго алгоритма может привести к неуда-
че; в таком случае, первый алгоритм проваливается до последнего варианта и получает результат Top.
Например, Bool Top {} Top Top.
Несложно проверить, что функции и всюду определены (т. е., их вычисление всегда заверша-
ется): заметим просто, что общий размер S и T становится меньше при каждом рекурсивном вызове.
Кроме того, алгоритм никогда не завершается неудачей, если его аргументы ограничены снизу.
Лемма A.0.10 Если L <: S и L <: T, то S T M для некоторого M.
Доказательство: Индукция по размеру S (или, что равносильно, T) с разбором вариантов формы S и
T. Если какой-либо из типов S или T равен Top, то применим один из двух первых вариантов опре-
деления, и результатом будет, соответственно, T или S. Случаи, когда S и T имеют разную форму,
возникнуть не могут, поскольку лемма об обращении отношения наследования (15.3.2) выдвигала бы
тогда противоречивые трабования к L; например, если S — функциональный тип, то таковым дол-
жен быть и L, но если при этом T — тип записей, то L также должен оказаться типом записей.
1
Остается три варианта.
Если S и T оба равняются Bool, то применим третий вариант определения, и задача решена.
Предположим тогда, что S S
1
S
2
и T T
1
T
2
. Алгоритм для в целом говорит нам, что
первый рекурсивный вызов имеет результатом некоторый тип J
1
. При этом по лемме об обращении,
L обязан иметь вид L
1
L
2
, причем L
2
<: S
2
и L
2
<: T
2
. А именно, L
2
является общей нижней гранью
S
2
и T
2
; таким образом, применимо предположение индукции, и мы знаем, что S
2
T
2
не завершается
неудачей, а возвращает какой-то тип M
2
. Таким образом, S T J
1
M
2
.
Наконец, предположим, что S {k
j
:S
j
j 1..m
}, а T {l
i
:T
i
i 1..n
}. По лемме об обращении, L
обязан быть типом записей, и его метки должны включать все метки, встречающиеся в S либо
T. Более того, для каждой метки, имеющейся как в S, так и в T, согласно лемме об обращении,
соответствующее поле в L будет общим подтипом S и T. Это гарантирует нам, что рекурсивные
вызовы алгоритма для всех общих меток полей будут успешны.
Теперь нужно убедиться, что наши алгоритмы вычисляют объединения и пересечения. Доказатель-
ство разбито на два утверждения: A.0.11 показывает, что вычисленное пересечение является общей
нижней гранью S и T, а объединение является верхней гранью; Утверждение A.0.12 показывает, что
вычисленное пересечение больше любой общей нижней грани S и T, а вычисленное объединение меньше
любой общей верхней грани.
1
Строго говоря, Лемма 15.3.2 не упоминает Bool. Дополнительный вариант для этого случая просто говорит, что
единственным подтипом Bool является он сам.
rev. 104

403
Утверждение A.0.11 1. Если S T J, то S <: J и T <: J.
2. Если S T M, то M <: S и M <: T.
Доказательство: Прямолинейная индукция по размеру «вывода» S T M или S T J (т. е., по
количеству рекурсивных вызовов определений и , требуемых для вычисления M либо J).
Утверждение A.0.12 1. Предположим, что S T J и, для некоторого U, S <: U и T <: U. Тогда
J <: U.
2. Предположим, что S T M и, для некоторого L, L <: M и L <: T. Тогда L <: M.
Доказательство: Две части леммы доказываются совместно, индукцией по размеру S и T (в сущно-
сти, подойдет индукция почти по чему угодно). Установим неизменными S и T и рассмотрим обе
части по очереди.
В части (1) рассмотрим варианты формы для U. Если U равняется Top, ничего доказывать не
надо, поскольку J <: Top при любом J. Если U Bool, то, согласно лемме об обращении, S и T также
должны равняться Bool, так что J Bool, и доказательство закончено. Остальные варианты более
интересны.
Если U U
1
U
2
, то, согласно лемме об обращении, S S
1
S
2
и T T
1
T
2
, причем U
1
<: S
1
, U
1
<: T
1
, S
2
<: U
2
и T
2
<: U
2
. Согласно предположению индукции, M
1
, пересечение
S
1
и T
1
, лежит выше U
1
, в то время как J
2
, объединение S
2
и T
2
, лежит ниже, чем U
2
. По
правилу S-Arrow, M
1
J
2
<: U
1
U
2
.
Если U — тип записей, то, согласно лемме об обращении, S и T также являются типами
записей. Более того, множества меток S и T — надмножества множества меток U, и
тип каждого поля U является надтипом типов соответствующих меток в S и T. Таким
образом, объединение S и T будет содержать по крайней мере метки U, и (по предположе-
нию индукции) поля объединения будут подтипами соответствующих полей U. По правилу
S-Rcd, J <: U.
В части (2) мы также рассматриваем варианты формы для S и T. Если один из этих типов Top,
то пересечение равно другому, и результат следует непосредственно. Варианты, когда S и T имеют
различную (не-Top) форму, возникнуть не могут, как мы уже видели в доказательстве A.0.10. Если
оба типа равны Bool, результат, опять же, следует непосредственно. Оставшиеся случаи (S и T
либо оба функциональные типы, либо оба типы записей) более интересны.
Если S S
1
S
2
и T T
1
T
2
, то, по лемме об обращении, имеем L L
1
L
2
, причем
S
1
<: L
1
, T
1
<: L
1
, L
2
<: S
2
и L
2
<: T
2
. По предположению индукции, J
1
, объединение S
1
и T
1
, лежит ниже L
1
, а M
2
, пересечение S
2
и T
2
, лежит выше L
2
. По правилу S-Arrow,
L
1
L
2
<: J
1
M
2
.
Если S и T — типы записей, то, по лемме об обращении, L также является типом записей.
Более того, L должен содержать все метки полей, имеющиеся в S или T (и, возможно,
какие-то еще), а соответствующие поля должны находиться в отношении наследования.
Для каждого поля m
l
в M, пересечении S и T, возможны три варианта. Если m
l
встречается
и в S, и в T, то его тип в M — пересечение его типов в S и T, а соответсвующий тип в L
является подтипом поля в M по предположению индукции. Если же m
l
встречается только
в S, соответствующий тип в M тот же, что и в S, и мы знаем, что тип в L меньше
него. Так же можно рассуждать и в том случае, если m
l
встречается только в T.
16.3.3. Решение: Минимальный тип этого терма Top — объединение Bool и {}. Однако то, что этот
терм типизируем, вероятно, должно рассматриваться как слабость нашего языка, поскольку трудно
себе представить, чтобы программист действительно хотел написать это выражение — в конце концов,
к значению типа Top нельзя применить никакую операцию, так что нет никакого смысла его вычислять!
Есть два способа отреагировать на эту слабость. Во-первых, можно просто исключить Top из системы,
и сделать частичной операцией. Во-вторых, можно сохранить Top, но заставить программу проверки
типов выдавать предупреждение каждый раз, когда обнаруживается терм с минимальным типом Top.
rev. 104

404
16.3.4. Решение: Обработка типов Ref не представляет сложности. Нужно просто добавить по вари-
анту в алгоритмы, вычисляющие объединение и пересечение:
S T =
. . . . . .
Ref(T
1
) если S Ref(S
1
), T Ref(T
1
), S
1
<: T
1
и T
1
<: S
1
. . . . . .
S T =
. . . . . .
Ref(T
1
) если S Ref(S
1
), T Ref(T
1
), S
1
<: T
1
и T
1
<: S
1
. . . . . .
Однако если мы разбиваем Ref на конструкторы Source и Sink, возникает существенная труд-
ность: отношение наследования больше не обладает объединениями (и пересечениями)! Например, типы
Ref{a:Nat,b:Bool} и Ref{a:Nat} являются подтипами как Source{a:Nat}, так и Sink{a:Nat,b:Bool},
а у этих двух типов нет наибольшей нижней грани.
Есть несколько способов справиться с этой трудностью. Возможно, самый простой — добавить в
систему либо Source, либо Sink, но не оба вместе. Для многих областей приложений, этого окажется
достаточно. Например, для уточненной реализации классов в §18.12 нам требуется только Source. В па-
раллельном языке с типами каналов (§15.5.7), наоборот, выгоднее использовать только Sink, поскольку
при этом мы сможем определить процесс-сервер и передавать между процессами только «право посы-
лать данные» в его канал доступа (право получать данные требуется только самому процессу-серверу).
Если имеются только типы Source, алгоритм вычисления объединений остается полным, будучи
расширен следующим образом (нужны также варианты для Ref, приведенные выше; аналогичные ва-
рианты нужно добавить в алгоритм вычисления пересечений):
S T =
. . . . . .
Source(J
1
) если S Ref(S
1
), T Ref(T
1
), S
1
T
1
J
1
Source(J
1
) если S Source(S
1
), T Source(T
1
), S
1
T
1
J
1
Source(J
1
) если S Ref(S
1
), T Source(T
1
), S
1
T
1
J
1
Source(J
1
) если S Source(S
1
), T Ref(T
1
), S
1
T
1
J
1
. . . . . .
Еще одно решение (предложенное Хеннеси и Рили, Hennessy and Riely 1998) состоит в том, чтобы
модифицировать конструктор Ref, чтобы он вместо одного принимал два аргумента: элементы типа
Ref S T — ссылочные ячейки, куда можно записывать элементы типа S, и откуда можно считывать
элементы типа T. Новый конструктор Ref контравариантен по первому параметру и ковариантен по
второму. Теперь можно определить Sink S как сокращение для Ref S Top, а Source T как Ref Bot T.
16.4.1. Решение: Да:
Γ t
1
: T
1
T
1
Bot Γ t
2
: T
2
Γ t
3
: T
3
T
2
T
3
T
Γ if t
1
then t
2
else t
3
: T
(TA-If)
Альтернатива
Γ t
1
: T
1
T
1
Bot Γ t
2
: T
2
Γ t
3
: T
3
Γ if t
1
then t
2
else t
3
: Bot
(TA-If)
кажется привлекательной, и была бы безопасна (поскольку тип Bot пуст, вычисление t
1
все равно не
может привести к обыкновенному результату), но по такому правилу получат типы некоторые термы,
не являющиеся типизируемыми согласно декларативным правилам; оно сломало бы Теорему 16.2.4.
17.3.1. Решение: Для решения задачи достаточно перевести на ML алгоритмы из Упражнения 16.3.2.
let rec join ctx tyS tyT =
if subtype ctx tyS tyT then tyT else
if subtype ctx tyT tyS then tyS else
let tyS = simplifyty ctx tyS in
let tyT = simplifyty ctx tyT in
match ( tyS , tyT ) with
( TyRe c ord ( fS ), TyRecord ( fT )) ->
let label sS = List . map ( fun (li ,_ ) -> li ) fS in
let label sT = List . map ( fun (li ,_ ) -> li ) fT in
let c o m m o n L a b e ls =
List . f i nd_all ( fun l -> List . mem l label sT ) label sS in
rev. 104

405
let c o m m o n F i e l d s =
List . map ( fun li ->
let tySi = List . assoc li fS in
let tyTi = List . assoc li fT in
(li , join ctx tySi tyTi ))
commonLabels in
TyR ecord ( c o m m o n F i e l d s )
| ( TyArr ( tyS1 , tyS2 ), TyArr ( tyT1 , tyT2 )) ->
( try TyArr ( meet ctx tyS1 tyT1 , join ctx tyS2 tyT2 )
with N ot_found -> TyTop )
| _ ->
TyTop
and meet ctx tyS tyT =
if subtype ctx tyS tyT then tyS else
if subtype ctx tyT tyS then tyT else
let tyS = simplifyty ctx tyS in
let tyT = simplifyty ctx tyT in
match ( tyS , tyT ) with
( TyRe c ord ( fS ), TyRecord ( fT )) ->
let label sS = List . map ( fun (li ,_ ) -> li ) fS in
let label sT = List . map ( fun (li ,_ ) -> li ) fT in
let allLabels =
List . append
la belsS
( List . f ind_all
( fun l -> not ( List . mem l labels S )) l abelsT ) in
let allFields =
List . map ( fun li ->
if List . mem li allL a bels then
let tySi = List . assoc li fS in
let tyTi = List . assoc li fT in
(li , meet ctx tySi tyTi )
else if List . mem li labelsS then
(li , List . assoc li fS )
else
(li , List . assoc li fT ))
all L a bels in
TyR ecord ( allFields )
| ( TyArr ( tyS1 , tyS2 ), TyArr ( tyT1 , tyT2 )) ->
TyArr ( join ctx tyS1 tyT1 , meet ctx tyS2 tyT2 )
| _ ->
raise N o t_found
let rec type of ctx t =
match t with
...
| TmTrue ( fi ) ->
Ty Bool
| TmFalse ( fi ) ->
Ty Bool
| TmIf ( fi ,t1 , t2 , t3 ) ->
if subtype ctx ( typeof ctx t1 ) TyBool then
join ctx ( typeof ctx t2 ) ( typeo f ctx t3 )
else err or fi "условие␣в␣условном␣выражении␣не␣типа␣ Bool "
17.3.2. Решение: См. интерпретатор rcdsubbot.
18.6.1. Решение:
DecC o u n t e r = { get :Unit - > Nat , inc : Unit -> Unit , reset : Unit - > Unit ,
rev. 104

406
dec :Unit - > Unit };
decCounterClas s =
λr : Co u n t erRep .
let super = resetCounter C l a s s r in
{ get = super . get ,
inc = super .inc ,
reset = super . reset ,
dec = λ_ : Unit . r. x := pred (!( r.x ))};
18.7.1. Решение:
BackupCounter2 = { get : Unit -> Nat , inc : Unit -> Nat ,
reset : Unit - > Unit , backup : Unit -> Unit ,
re set2 : Unit -> Unit , backup2 : Unit -> Unit };
BackupCou n t e r R ep 2 = { x : Ref Nat , b: Ref Nat , b2 : Ref Nat };
backupC o u n t er C l as s 2 =
λr : BackupCoun t e r R e p2 .
let super = backupCount e r C la s s r in
{ get = super . get , inc = super . inc ,
reset = super . reset , backu p = super . backup ,
re set2 = λ_: Unit . r . x :=!( r . b2 ),
ba ckup2 = λ_: Unit . r .b2 :=!( r.x )};
18.11.1. Решение:
instrCoun t e r C l as s =
λr : InstrCounterRep .
λself : Unit -> InstrCounter .
λ_ : Unit .
let super = se tC o u n t e r Cl a s s r self unit in
{ get = λ_: Unit . (r.a := succ (!( r.a )); super . get unit ) ,
set = λi : Nat . (r. a := succ (!( r.a )); suer . set i),
inc = super .inc ,
acc esses = λ_: Unit . !( r.a )};
ResetInst r C o u n te r = { get : Unit - >Nat , set : Nat -> Unit ,
inc :Unit - > Unit , access e s : Unit - > Nat ,
reset : Unit - > Unit };
resetI n s t rC o un t er C la s s =
λr : InstrCounterRep .
λself : Unit -> R e s e tI n s t rC o u n te r .
λ_ : Unit .
let super = instrCounter C l a s s r self unit in
{ get = super . get ,
set = super .set ,
inc = super .inc ,
acc esses = super . accesses ,
reset = λ_ : Unit . r. x :=0};
BackupIn s t r C ou n t e r = { get : Unit - >Nat , set : Nat -> Unit ,
inc :Unit - > Unit , access e s : Unit - > Unit ,
ba ckup : Unit -> Unit , reset : Unit - > Unit };
Backup I n s tr C o un t er R e p = { x : Ref Nat , a: Ref Nat , b: Ref Nat };
backup I n st r C ou nt e rC l as s =
λr : Backup I n s tr C o un t er R e p .
rev. 104

407
λself : Unit -> B a c ku p I n st r C ou n t e r .
λ_ : Unit .
let super = resetIn s t r Co u nt e r Cl a ss r self unit in
{ get = super . get ,
set = super .set ,
inc = super .inc ,
acc esses = super . accesses ,
reset = λ_ : Unit . r. x :=!( r. b ),
ba ckup = λ_: Unit . r . b :=!( r . x )};
newBac k u p In s t rC o un t e r =
λ_ : Unit . let r = {x= ref 1 , a = ref 0, b= ref 0} in
fix ( backup I n s tr C ou n te r Cl a ss r ) unit ;
18.13.1. Решение: Один из способов проверки на тождественность — использовать ссылочные ячейки.
Мы расширяем внутреннее представление наших объектов переменной экземпляра id типа Ref Nat
IdCounterRep = { x: Ref Nat , id : Ref ( Ref Nat )};
и добавляем метод id, который просто возвращает поле id:
IdC o u nter = { get : Unit -> Nat , inc : Unit -> Unit , id : Unit - >( Ref Nat )};
idCounterClass =
λr : IdCounterRe p .
{ get = λ_: Unit . !( r.x ) ,
inc = λ_ : Unit . r. x := succ (!( r.x )) ,
id = λ_: Unit . !( r. id )};
Теперь функция sameObject может просто взять два объекта с методами id и проверить, одинаковые
ли ссылки возвращают эти два метода id.
same O b j e c t =
λa :{ id : Unit - >( Ref Nat )}. λb :{ id :Unit - >( Ref Nat )}.
(( b. id unit ) := 1,
(a. id unit ) := 0 ,
is zero (!( b. id unit )));
Фокус состоит в том, что можно проверить две ссылки на равенство, попытавшись использовать их
как псевдонимы друг друга: мы делаем содержимое второй ссылки ненулевым, потом присваиваем ноль
первой ссылке, а затем смотрим содержимое второй и проверяем, не стало ли оно нулем.
19.4.1. Решение: Поскольку каждое объявление класса должно содержать выражение extends, и по-
скольку циклическая зависимость между этими выражениями запрещена, цепочка выражений extends,
ведущая от каждого класса, должна в конце концов привести к Object.
19.4.2. Решение: Один очевидный способ улучшить язык — объединить три правила для приведений
в одно:
Γ t
0
: D
Γ (C)t
0
: C
(T-Cast)
и отказаться от понятия глупого приведения. Еще один — убрать конструкторы, поскольку они все
равно ничего не делают.
19.4.6. Решение:
1. Формулировка правил для интерфейсов в FJ труда не представляет.
2. Допустим, мы определяем следующие интерфейсы:
int e r face A {}
int e r face B {}
int e r face C ex tends A ,B {}
int e r face D ex tends A ,B {}
rev. 104

408
В такой ситуации C и D имеют в качестве общих верхних граней как A, так и B, но не имеют точной
верхней грани.
3. Вместо стандартного алгоритмического правила для условных выражений
Γ t
1
: boolean Γ t
1
: E
2
Γ t
3
: E
3
Γ t
1
? t
2
: t
3
: E
2
E
3
в Java используются следующие ограниченные правила:
Γ t
1
: boolean Γ t
1
: E
2
Γ t
3
: E
3
Γ E
2
<: E
3
Γ t
1
? t
2
: t
3
: E
3
Γ t
1
: boolean Γ t
1
: E
2
Γ t
3
: E
3
Γ E
3
<: E
2
Γ t
1
? t
2
: t
3
: E
2
Интуитивно, эти правила корректны, но они плохо сочетаются с операционной семантикой с малым
шагом, принятой в FJ — свойство сохранения типов оказывается ложным! (Нетрудно построить пример,
демонстрирующий это.)
19.4.7. Решение: Как ни странно, обработка super оказывается сложнее, чем self, поскольку требуется
каким-то образом запоминать, из какого класса происходит «выполняемый в данный момент» метод.
Есть по крайней мере два способа это сделать:
1. Снабжать термы аннотацией, указывающей, где нужно искать значение super.
2. Добавить шаг предварительной обработки, гле переписывается вся таблица классов, и все упо-
минания super переводятся в отсылки к this с «исковерканными» именами, указывающими, из
какого класса эти отсылки происходят.
19.5.1. Решение: Прежде, чем представить полное доказательство, мы вводим несколько вспомога-
тельных лемм. Как всегда, самая важная из них (A.0.14) связывает типизацию и подстановку.
Лемма A.0.13 Если mtype m, D C C
0
, то mtype m, C C C
0
для всех C <: D.
Доказательство: Прямолинейная индукция по дереву вывода C <: D. Заметим, что, независимо
от того, определен ли метод m в CT C или нет, mtype m, C должен оставаться таким же, как
mtype m, E , где CT C class C extends E {...}.
Лемма A.0.14 Подстановка термов сохраняет типизацию : Если Γ, x:B t : D и Γ s : A,
где A <: B, то Γ x s t : C для некоторого C <: D.
Доказательство: Индукция по дереву вывода Γ, x:B t : D. Интуитивные шаги те же самые, что
и в лямбда-исчислении с наследованием; детали, разумеется, немного отличаются. Самые важные
варианты — два последних.
Вариант T-Var: t x x:D Γ
Если x x, результат тривиален, поскольку x s x x. С другой стороны, если x x
i
, а D B
i
,
то, поскольку x s x s
i
, достаточно положить C A
i
.
Вариант T-Field: t t
0
.f
i
Γ, x:B t
0
: D
0
fields D
0
C f D C
i
Согласно предположению индукции, существует некоторый C
0
, такой, что x s t
0
: C
0
и C
0
<:
D
0
. Нетрудно проверить, что fields C
0
fields D
0
, D g для некоторых D g. Следовательно, по пра-
вилу T-Field, Γ ( x s t
0
).f
i
: C
i
.
Вариант T-Invk: t t
0
.m(t) Γ, x:B t
0
: D
0
mtype m, D
0
E D
Γ, x:B t : D D <: E
По предположению индукции, существуют такие C
0
и C, что:
Γ, x s t
0
: C
0
C
0
<: D
0
Γ, x s t : C C <: D
По Лемме A.0.13, mtype m, C
0
E D. Более того, C <: E по транзитивности <:. Следовательно,
по правилу T-Invk, Γ x s t
0
.m( x s t) : D.
rev. 104
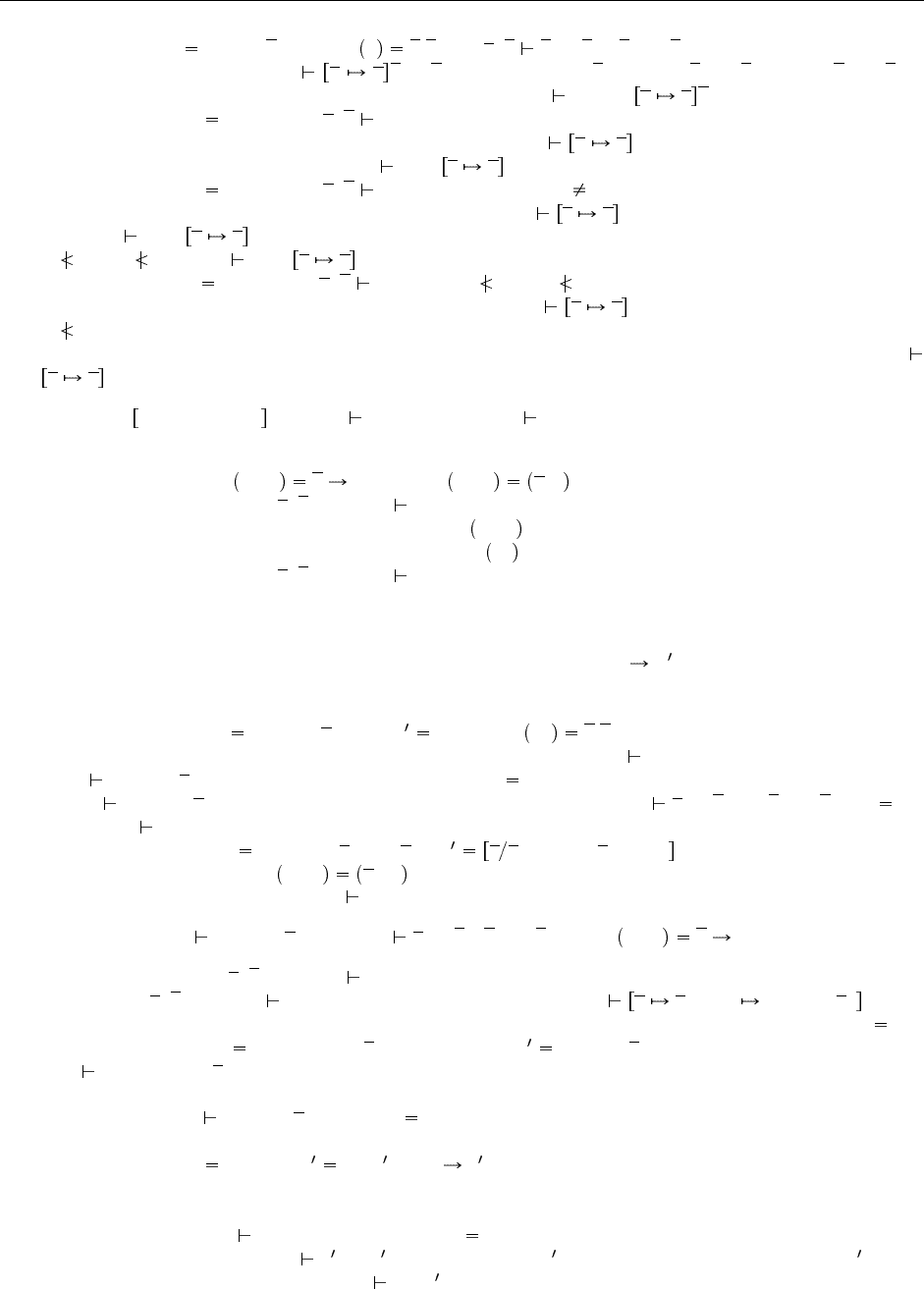
409
Вариант T-New: t new D(t) fields D D f Γ, x:B t : C C <: D
По предположению индукции, Γ x s t : E для некоторых E, причем E <: C. Имеем E <: D по
транзитивности <:. Следовательно, пр правилу T-New, Γ new D( x s t) : D.
Вариант T-UCast: t (D)t
0
Γ, x:B t
0
: C C <: D
По предположению индукции, существует такой E, что Γ x s t
0
: E и E <: C. Имеем E <: D
по транзитивности <:, что дает нам Γ (D)( x s t
0
) : D по правилу T-UCast.
Вариант T-DCast: t (D)t
0
Γ, x:B t
0
: C D <: C D C
По предположению индукции, существует такой E, что Γ x s t
0
: E и E <: C. Если E <: D или
D <: E, то Γ (D)( x s t
0
) : D, соответственно, по T-UCast или T-DCast. С другой стороны,
если D : E и E : D, то Γ (D)( x s t
0
) : D (c предупреждением о глупости) по правилу T-SCast.
Вариант T-SCast: t (D)t
0
Γ, x:B t
0
: C D : C C : D
По предположению индукции, существует такой E, что Γ x s t
0
: E и E <: C. Это означает,
что E : D. (Чтобы увидеть это, заметим, что у каждого класса в FJ есть только один надкласс.
Отсюда следует, что, если E <: C и E <: D, то либо C <: D, либо D <: C.) Таким образом, Γ
(D)( x s t
0
) : D (c предупреждением о глупости) по правилу T-SCast.
Лемма A.0.15 Ослабление : Если Γ t : C, то Γ, x:D t : C.
Доказательство: Прямолинейная индукция.
Лемма A.0.16 Если mtype m, C
0
D D, а mbody m, C
0
x, t , то для некоторого D
0
и некоторого C
<: D выполняется C
0
<: D
0
и x:D, this:D
0
t : C.
Доказательство: Индукция по дереву вывода mbody m, C
0
. Базовый случай (когда m определен внутри
C
0
) доказывается просто, поскольку m определен в CT C
0
, и из корректности таблицы классов прямо
следует, что мы уже вывели x:D, this:D
0
t : C по правилу T-Method. Шаг индукции также не
представляет труда.
Теперь мы готовы дать доказательство теоремы о типовой безопасности.
Доказательство Теоремы 19.5.1: Индукция по дереву вывода t t , с разбором вариантов по-
следнего правила. Обратите внимание, как в подварианте T-DCast (предпоследнем) порождаются
предупреждения о глупости.
Вариант E-ProjNew: t new C
0
(v).f
i
t v
i
fields C
0
D f
По форме t мы можем определить, что последнее правило в выводе Γ t : C было T-Field, с предпо-
сылкой Γ new C
0
(v) : D
0
, для некоторого D
0
, и что C D
i
. Подобным образом, последним правилом
в выводе Γ new C
0
(v) : D
0
должно быть T-New, с предпосылками Γ v : C при C <: D и D
0
C
0
.
В частности, Γ v
i
: C
i
, что завершает рассмотрение данного варианта, поскольку C
i
<: D
i
.
Вариант E-InvkNew: t (new C
0
(v)).m(u) t u x, new C
0
(v)/this t
0
mbody m, C
0
x, t
0
Последними правилами при выводе Γ t : C должны быть T-Invk и T-New, с предпосылками
Γ new C
0
(v) : C
0
Γ u : C C <: D mtype m, C
0
D C
По Лемме A.0.16, имеем x:D, this:D
0
t
0
: B для некоторых D
0
и B, причем C
0
<: D
0
и B <: C. По
Лемме A.0.15, Γ, x:D, this:D
0
t
0
: B. Отсюда, по Лемме A.0.14, Γ x u, this new C
0
(v) t
0
: E
для некоторого E <: B. По транзитивности <:, получаем E <: C. Теперь достаточно принять C’ E.
Вариант E-CastNew: t (D)(new C
0
(v)) C
0
<: D t new C
0
(v)
Вывод Γ (D)(new C
0
(v)) : C должен завершаться правилом T-UCast, поскольку, если бы он конча-
ся на T-SCast или T-DCast, получалось бы противоречие с предположением C
0
<: D. Предпосылки
T-UCast дают нам Γ new C
0
(v) : C
0
и D C, что завершает рассмотрение этого варианта.
Варианты с правилами соответствия не представляют труда. Мы рассмотрим только одно:
Вариант RC-Cast: t (D)t
0
t (D)t
0
t
0
t
0
Существует три подварианта, в зависимости от того, каково было последнее использованное правило
типизации.
Подвариант T-UCast: Γ t
0
: C
0
C
0
<: D D C
По предположению индукции, Γ t
0
: C
0
для некоторого C
0
<: C
0
. По транзитивности <:, C
0
<: C.
Следовательно, по правилу T-UCast, Γ (C)t
0
: C (без дополнительного предупреждения о глупо-
сти).
rev. 104

410
Подвариант T-DCast: Γ t
0
: C
0
D <: C
0
D C
По предположению индукции, Γ t
0
: C
0
для некоторого C
0
<: C
0
. Если C
0
<: C либо C <: C
0
, имеем
Γ (C)t
0
: C по правилу T-UCast либо T-DCast (без дополнительного предупреждения о глупо-
сти). Если же C
0
: C и C : C
0
, то Γ (C)t
0
: C с предупреждением о глупости по правилу T-SCast.
Подвариант T-SCast: Γ t
0
: C
0
D : C
0
C
0
: D D C
По предположению индукции, Γ t
0
: C
0
для некоторого C
0
<: C
0
. В таком случае выполняются
также C
0
: C и C : C
0
. Следовательно, Γ (C)t
0
: C с предупреждением о глупости.
20.1.1. Решение:
Tree = µX . <leaf : Unit , node :{ Nat ,X ,X } >;
leaf = < leaf =unit > as Tree ;
leaf : Tree
node = λn : Nat . λt
1
: Tree . λt
2
: Tree . <node ={ n, t
1
,t
2
}> as Tree ;
node : Nat -> Tree -> Tree -> Tree
is leaf = λl: Tree . case l of <leaf =u > => true | < node =p > = > false ;
is leaf : Tree -> Bool
label = λl : Tree . case l of < leaf =u > = > 0 | <node =p > => p .1;
label : Tree -> Nat
left = λl : Tree . case l of < leaf =u > = > leaf | < node =p > = > p .2;
left : Tree -> Tree
right = λl : Tree . case l of < leaf =u > = > leaf | < node =p > = > p .3;
right : Tree -> Tree
ap pend = fix (λf: NatList - > NatList -> NatLis t .
λl1 : Na tList . λl2 : N atList .
if isnil l1 then l2 else
cons ( hd l1 ) ( f ( tl l1 ) l2 ));
ap pend : NatList -> N atList -> NatList
pre order = fix (λf: Tree - > NatList . λt: Tree .
if isle af t then nil else
cons ( label l)
( ap pend (f ( left t )) ( f ( right t ))));
pre order : Tree -> NatL ist
t1 = node 1 leaf leaf ;
t2 = node 2 leaf leaf ;
t3 = node 3 t1 t2 ;
t4 = node 4 t3 t3 ;
l = preorder t4 ;
hd l ;
4 : Nat
hd ( tl l )
rev. 104
