Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

30.3. Свойства исчисления 351

30.3.3. Сохранение

Мы почти готовы приступить к главному доказательству, что типы сохраняются при редукции.

Есдинственное, что нам осталось перед этим доказать — это, как обычно, лемма об инверсии, которая

при данном выводе типа, чье заключение имеет определенную форму, сообщает нам, как выглядят

подвыводы. В свою очередь, эта лемма зависит от простого утверждения, касающегося параллельной

редукции.

Лемма 30.3.12 1. Если S

V T, то T T

, причем S

V T

и S

V T

2. Если X::K

V T, то T X::K

, причем S

V T

Доказательство: Прямолинейная индукция.

Лемма 30.3.13 Инверсия :

1. Если Γ λx:S

. s

: T

, то T

и Γ, x:S

: T

. Кроме того, Γ S

:: *.

2. Если Γ λX::J

. s

: X::K

, то J

и Γ, X::J

: T

Доказательство: В части 1 мы доказываем по индукции следующее несколько более сильное утвер-

ждение: если Γ λx:S

. s

: S и S T

, то T

и Γ, x:S

: T

. Шаг индукции, правило

T-Eq, труда не представляет. Интересен базовый шаг, правило T-Abs. Здесь S имеет вид S

где Γ, x:S

: S

. По Лемме 30.3.12(1) имеем T

и T

, откуда правило T-Eq дает нам

Γ, x:S

: T

. Более того, из второй предпосылки правила T-Abs получаем Γ S

:: *. Часть

2 доказывается подобным же образом.

Теорема 30.3.14 Сохранение : Если Γ t :T и t t’, то Γ t’ : T.

Доказательство: Прямолинейная индукция по деревьям вывода типов. Построение доказательства

подобно доказательству теоремы о сохранении для простого типизированного лямбда-исчисления с

наследованием (15.3.5).

Вариант T-Var: t x

Не может возникнуть (правил вычисления для переменных не существует).

Вариант T-Abs: t λx:T

Не может возникнуть (t уже является значением).

Вариант T-App: t t

Γ t

: T

Γ t

: T

T T

Из Рис. 30.1 видно, что t t’ может быть выведено через три различных правила: E-App1, E-

App2 и E-AppAbs. Для первых двух из них требуемый результат прямо следует из предположения

индукции. Третье правило интереснее:

Подвариант E-AppAbs: t

λx:S

t’ x v

Согласно Лемме 30.3.13(1), T

и Γ, x:S

: T

. По правилу T-Eq, Γ

: S

. Отсюда при помощи леммы о подстановке (30.3.3) получаем Γ t’ : T

Вариант T-TAbs: t λX::K

Не может возникнуть (t уже является значением).

Вариант T-TApp: t t

] Γ t

: X::K

Γ T

:: K

T X T

Подобен варианту T-App, но вместо леммы о подстановке термов (30.3.3) используется лемма о

подстановке типов (30.3.4).

Вариант T-Eq: Γ t : S S T Γ T :: *

Согласно предположению индукции, Γ t’ : S. По правилу T-Eq, Γ t’ : T.

30.3.4. Продвижение

Следующей нашей задачей будет теорема о продвижении. Снова большая часть необходимых для

доказательства свойств у нас уже имеется — требуется только стандартная лемма о канонических

формах, говорящая о формах замкнутых значений.

rev. 104

352 30.3. Свойства исчисления

Лемма 30.3.15 Канонические формы :

1. Если t — замкнутое значение и t : T

, то t является абстракцией.

2. Если t — замкнутое значение и t : X::K

, то t является абстракцией типа.

Доказательство: Рассуждения в двух частях леммы подобны друг другу; мы приводим только часть

(1). Поскольку имеются только две формы значений, если t является значением и не является аб-

стракцией, это должна быть абстракция типа. Так что предположим (чтобы вывести противо-

речие), что это абстракция типа. Тогда данное нам дерево вывода для t : T

должно за-

вершаться экземпляром T-TAbs, за которым может следовать некоторое количество экземпляров

T-Eq. То есть, оно должно иметь следующую форму (мы опускаем предпосылки, касающиеся видов):

t : X::K

T-TAbs

X::K

t : U

n 1

T-Eq

n 1

t : U

T-Eq

t : T

T-Eq

Поскольку эквивалентность типов транзитивна, все эти эквивалентности мы можем слить в одну

и заключить, что X::K

. Однако тогда, исходя из Утверждения 30.3.10, должен су-

ществовать некоторый тип U, такой, что X::K

V U и T

V U. Согласно Лемме 30.3.12,

тип U должен в качестве главного конструктора одновременно иметь квантор и стрелку — это про-

тиворечие.

Теорема 30.3.16 Продвижение : Допустим, имеется замкнутый правильно типизированный

терм t (т. е., t : T для некоторого типа T). Тогда либо t является значением, либо существует

некоторый терм t’, такой, что t t’.

Доказательство: Индукция по деревьям вывода типов. Вариант T-Var возникнуть не может, по-

скольку t замкнут. В вариантах T-Abs и T-TAbs утверждение теоремы следует немедленно, по-

скольку абстракции являются значениями. В варианте T-Eq требуемое утверждение непосред-

ственно следует из предположения индукции. Оставшиеся два случая, применение и применение

типа, представляют больший интерес. Мы приводим рассуждение только для случая применения

типа; вариант простого применения доказывается подобным же образом.

Вариант T-TApp: t t

] t

: X::K

:: K

Согласно предположению индукции, либо t

является значением, либо он может проделать шаг

вычисления. Если он может проделать шаг, то к t применимо правило E-TApp. Если же терм t

— значение, то благодаря лемме о канонических формах (30.3.15) нам известно, что t

является

абстракцией типа, так что к t применимо правило E-TAppTAbs.

Упражнение 30.3.17 Рекомендуется, : Допустим, что мы добавили к отношению эквивалент-

ности типов следующее странное правило:

T T X::*.T

Какие основные свойства системы окажутся ложными (если какие-то окажутся)? С другой сторо-

ны, допустим, мы добавили правило:

S T T S

Какие свойства сломаются в этом случае?

rev. 104

30.3. Свойства исчисления 353

30.3.5. Присвоение видов

В определении F

на Рис. 30.1 мы потратили некоторые усилия, добиваясь, чтобы все типы, которые

мы можем присвоить термам согласно нашим правилам, имели правильные виды. В частности, в пра-

виле T-Abs мы проверяем, прежде чем добавляем аннотацию типа из лямбда-абстракции в контекст,

что она правильно сформирована, а в T-Eq проводится проверка, что тип T, приписываемый терму t,

принадлежит виду *. Точная формулировка условия правильного построения, которое эти проверки

обеспечивают, дана в следующем утверждении.

Определение 30.3.18 Говорится, что контекст Γ правильно построен, если (1) Γ пуст, либо (2) Γ

, x:T, где Γ

правильно построен и Γ T :: *, либо (3) Γ Γ

, X::K и Γ

правильно построен.

Утверждение 30.3.19 Если Γ t : T и Γ правильно построен, то Γ T :: *.

Доказательство: Несложная индукция, с использованием Леммы 30.3.4(1) в варианте T-TApp.

30.3.6. Разрешимость

Из-за недостатка места мы не можем привести в этой книге полное доказательство разрешимости

для F

— т. е., алгоритм проверки типов, а также доказательства его корректности, полноты и гарантии

завершения, — но почти все требуемые для такого доказательства идеи уже знакомы нам из алгоритма

поиска минимальных типов для Системы F

в Главе 28.

Для начала мы замечаем, что отношение присвоения видов разрешимо (поскольку его правила

управляются синтаксисом). Это неудивительно, поскольку, как мы видели, виды по существу явля-

ются копией простого типизированного лямбдда-исчисления «уровнем выше». Это убеждает нас, что

проверки правильного присвоения видов в правилах типизации могут быть эффекивно реализованы.

Затем мы удаляем из отношения типизации единственное правило, не управляемое синтаксисом, T-

Eq — так же, как мы удаляли T-Sub из F

. Мы рассматриваем остальные правила и выясняем, какие

предпосылки требуют обобщения, чтобы заменить случаи существенного использования исключенного

T-Eq. Оказывется, что таких критических точек две.

1. В первой предпосылке правил T-App и T-TApp может потребоваться применить T-Eq, чтобы

переписать тип левого подвыражения t

и вынести стрелку или квантор наружу. (Например, если

в контексте переменная x связана с типом (λX.X X) Nat, то терм-применение x 5 имеет тип Nat

только потому, что тип x может быть переписан как Nat Nat.)

Мы добиваемся цели, введя аналог отношения выявления из §28.1. Здесь, вместо того, чтобы

повышать минимальный тип t

, пока он не станет функциональным или кваторным типом, мы

проводим его редукцию — например, многократно применяя правила с Рис. 30.3, пока дальнейшая

редукция не станет невозможной.

Чтобы убедиться, что этот процесс придет к завершению, нужно показать, что наши правила ре-

дукции обладают свойством нормализации. Разумеется, на термах с нарушением видов редукция

не будет нормализующей, поскольку в синтаксисе F

имеется все необходимое для того, чтобы

закодировать незавершающиеся термы вроде omega (стр. 58). К счастью, из Утверждения 30.3.19

следует, что, если мы начнем с правильно построенного контекста (и в процессе будем прово-

дить проверки правильного видообразования, убеждаясь, что каждая аннотация, вносимая нами

в контекст, имеет правильный вид), то все термы, с которыми мы будем работать, будут иметь

правильные виды. А для таких термов можно показать (например, модифицировав методы Гла-

вы 12), что редукция всегда приводит к единственной нормальной форме.

2. Во второй предпосылке правила T-App может оказаться необходимым применить эквивалент-

ность типов, чтобы сопоставить тип T

, вычисленный для терма t

, с типом аргумента T

функци-

онального типа терма t

. Следовательно, алгоритмический вариант этого правила должен вклю-

чать проверку эквивалентности типов T

и T

. Такую проверку можно реализовать, например,

На самом деле большинство программ проверки типов для F

используют менее агрессивную разновидность редук-

ции, известную как слабая заголовочная редукция. При этом сокращаются только самые левые самые внешние редексы,

и как только какой-то конкретный конструктор — т. е., нечто отличное от применения, — оказывается в начале типа,

процесс останавливается.

rev. 104

354 30.4. Фрагменты F

сведя оба этих типа к нормальным формам, а затем проверив, совпадают ли они с точностью до

имен связанных переменных.

Упражнение 30.3.20 : Напишите программу проверки типов для F

на основе изложенных

здесь идей. В качестве отправной точки можно использовать интерпретатор purefsub.

30.4. Фрагменты F

Интуитивно понятно, что F

включает в себя λ и Систему F. Эту интуицию можно выразить

точно, определив иерархию систем F

, F

и т. д., так что пределом этой иерархии будет F

Определение 30.4.1 В Системе F

единственным видом является *, и не разрешается ни квантифи-

кация ( ), ни абстракция (λ) над типами. Остальные системы определяются относительно иерархии

видов уровня i, которая выглядит следующим образом:

i 1

* J K J K

и K K

i 1

1 i

В Системе F

у нас по-прежнему единственным видом является * и нет лямбда-абстракции на

уровне типов, но разрешена квантификация по простым типам (вида *). В F

разрешается кванти-

фикация по операторам над типами (т. е., можно выписывать выражения типа, имеющие форму

X::K.T, где K K

), и можно вводить абстракцию над простыми типами (т. е., мы рассматрива-

ем выражения в форме λX::*.T и присваиваем им виды вроде * *). В общем случае, F

i 1

позволяет

квантификацию над типами с видами из K

i 1

и абстракцию над типами с видами из K

представляет собой обычное простое типизированное лямбда-исчисление, λ . Его определение

выглядит поверхностно сложнее, чем на Рис. 9.1, поскольку включает отношения присвоения вида и эк-

вивалентности типов. Однако и то, и другое отношение тривиальны: всякий синтаксически правильный

тип имеет правильный вид, а именно *, а единственный тип, эквивалентный T — сам T. F

совпадает с

нашей Системой F; из-за этой его позиции в иерархии его часто называют лямбда-исчислением второго

порядка. F

— первая система, где отношения присвоения вида и эквивалентности типов оказываются

невырожденными.

Интересно, что все программы в этой книге содержатся в F

. (Строго говоря, операторы над типами

Object и Class из Главы 32 попадают в F

, поскольку их аргументом служит оператор над типами

вида (* *) *, но и тот, и другой можно рассматривать как сокращение, часть метаязыка, а не пол-

ноценное выражение исчисления — так мы поступали до Главы 29 с Pair, — поскольку в примерах с

Object и Class не требуется квантификация по типам этого вида.) С другой стороны, ограничение

нашего языка программирования рамками F

вместо полного F

никакого особенного упрощения не

дает, ни в сложности реализации, ни в метатеоретической изощренности, поскольку уже на этом уровне

присутствуют основные механизмы — абстракция операторов над типами и эквивалентность типов.

Упражнение 30.4.2 : Существуют ли полезные программы, выразимые в F

, но невырази-

мые в F

30.5. Идем дальше: зависимые типы

В этой книге много внимания уделялось формализации разнообразных механизмов абстракции.

В простом типизиованном лямбда-исчислении мы формализовали операцию вынесения подтерма из

терма, так что получается функция, которую затем можно конкретизировать, применяя ее к различ-

ным термам. В Системе F мы рассмотрели операцию вынесения из терма типа; при этом получается

терм, который можно конкретизировать, применяя его к различным типам. В λ

мы воспроизвели

механизм простого типизированного лямбда-исчисления «уровнем выше», и теперь можем выносить

подвыражение из типа и получать оператор над типами, который можно конкретизировать, применяя

к различным типам.

rev. 104

30.5. Идем дальше: зависимые типы 355

Удобно думать об этих разновидностях абстракции в терминах семейств выражений, которые ин-

дексируются другими выражениями. Обыкновенная лямбда-абстракция λx:T

представляет собой

семейство термов x s t

, проиндексированное термами s. Подобным образом, абстракция типа

λX::K

представляет собой семейство термов, проиндексированное типами, а оператор над типами

есть семейство типов, индексированное типами.

λx:T

семейство термов, индексированное термами

λX::K

семейство термов, индексированное типами

λX::K

семейство типов, индексированное типами.

При взгляде на этот список становится очевидно, что есть еще одна возможность, нами до сих пор не

рассмотренная: семейство типов, индексированное термами. Эта форма абстракции также подробно

изучена, под именем зависимых типов.

Зависимые типы позволяют достичь такой точности в описании поведения программ, которая идет

значительно дальше всех типовых конструкций, виденных нами до сих пор. В качестве простого при-

мера, допустим, у нас есть встроенный тип FloatList с обычными для такого типа операциями:

nil : FloatList

cons : Float -> FloatList -> Flo a t List

hd : F loatList -> Float

tl : F loatList -> Floa t List

isnil : F loatList -> Bool

В языке с зависимыми типами можно уточнить простой тип FloatList и заменить его семейством

типов FloatList n — каждый из которых представляет тип списка с n элементами.

Чтобы извлечь пользу из такого уточнения, мы изменяем типы базовых операций над списками.

Для начала приписываем константе nil тип FloatList 0. Чтобы приписать остальным операциям бо-

лее точные типы, требуется усовершенствовать способ записи функциональных типов, и позволить

выражать зависимость между их аргументами и типами результатов. Например, для cons требует-

ся примерно такой тип: «функция, принимающая Float и список длиной n, а возвращающая список

длиной n 1». Если мы сделаем связывание n явным, введя его как дополнительный аргумент, это

описание превращается в «функция, принимающая число n, элемент типа Float и список длиной n, и

возвращающая список длиной succ n». Таким образом, в типе нам нужно отразить зависимость между

значением первого аргумента (n) и типами третьего аргумента (FloatList n) и результата (FloatList

(succ n)). Для этого мы связываем с первым аргументом имя при помощи записи Πn:Nat. ... вместо

Nat .... При этом типы cons и других операций над списками превращаются в

nil : Flo a t List 0

cons : Πn : Nat . Float -> F l o atList n -> Fl oatList ( succ n)

hd : Πn: Nat . Fl oatList ( succ n) -> Float

tl : Πn: Nat . Fl oatList ( succ n) -> Float L ist n

Типы nil, cons и tl точно указывают, сколько элементов содержит их результат, а hd и tl требуют в

качестве аргументов непустые списки. Заметим также, что функция isnil больше не нужна, поскольку

проверить, пуст ли элемент FloatList n, можно путем простого сравнения n с 0.

Зависмые функциональные типы, имеющие форму Πx:T

, являются более точной формой функ-

циональных типов T

, где мы связываем переменную x, представляющую аргумент функции, и

получаем возможность упомянуть ее в типе результата T

. В вырожденном случае, когда x не встреча-

ется в T

, мы записываем Πx:T

как T

Разумеется, можно определять и новые термы с функциональными зависимыми типами. Например,

функция

con s t hree = λn : Nat . λf: Float . λl: F l oatList n.

cons ( succ ( succ n )) f

( cons ( succ n ) f

( cons n f l ));

приставляющая три копии своего второго аргумента (f) к началу третьего аргумента (l), имеет тип

Πn : Nat . Float -> F l oatList n -> Flo a t List ( succ ( succ ( succ n ))).

rev. 104

356 30.5. Идем дальше: зависимые типы

Заметим, что в каждом из трех вызовов cons первый аргумент имеет разное значение, что отражает

различную длину аргументов-списков.

В информатике и логике имеется общирная литература по зависимым типам. Хорошими отправ-

ными точками могут служить работы Смита, Нордстрема и Петерсона (Smith, Nordstr¨om and Peterson

1990), Томпсона (Thompson 1991), Луо (Luo 1994) и Хофмана (Hofmann 1997).

Упражнение 30.5.1 : То, что тип элементов списка жестко задан как Float, упрощает воспри-

ятие примера. Однако нетрудно обобщить его до списков произвольного типа T при помощи обыкно-

венных операторов над типами. Покажите, как это сделать.

Продолжая в том же духе, можно построить функции высшего порядка для работы со списками с

подобным же образом уточненными типами. Например, можно написать функцию сортировки, чей тип

sort : Πn : Nat . Fl o atList n -> Fl oatList n

говорит нам, что она возвращает список той же длины, что получает на входе. Более того, путем даль-

нейшего уточнения используемых семейств типов можно даже написать функцию sort так, чтобы ее

тип говорил, что возвращаемый список всегда отсортирован. Проверка, что функция sort принадлежит

этому типу, в сущности, окажется доказательством, что функция соответствует своей спецификации!

Такие примеры рисуют соблазнительную картину мира, где программы верны по построению, где

тип программы говорит нам все, что требуется знать о ее поведении, и одобрение от процедуры проверки

типов вселяет полную уверенность, что программа ведет себя как ожидается. Такое видение связано

с идеей программирования через «извлечение вычислительного содержимого» из доказательства, что

спецификацию возможно удовлетворить. Ключевое наблюдение состоит в том, что конструктивное

доказательство теоремы вида «Для каждого x существует y, такое, что P » можно рассматривать как

функцию, переводящую x в y, и снабженную информацией (вычислительно несущественной — т. е.,

представляющей интерес только для процедуры проверки типов), что эта функция обладает свойством

P . Эти идеи исследовались в рамках проектов Nuprl (Constable et al. 1986), LEGO (Luo and Pollack

1992; Pollack 1994), Coq (Paulin-Mohring 1989) и некоторых других.

К сожалению, мощность зависимых типов — обоюдоострое оружие. Размывание различий меж-

ду проверкой типов и доказательством произвольных теорем не приводит к волшебному облегчению

процесса доказательств — напротив, оно превращает проверку типов в вычислительно неразрешимую

задачу! Работа математика с программами механического содействия доказательству не состоит в том,

чтобы просто записать условие теоремы, нажать кнопку и ждать, пока программа ответит «Да» или

«Нет»: требуются значительные усилия по написанию сценариев доказательств и тактик, помогаю-

щих инструменту построить и верифицировать доказательство. Если идея правильности по построению

будет доведена до логического конца, можно ожидать, что программисты будут тратить сопоставимые

усилия по аннотации программ подсказками и объяснениями, помогающими программе проверки ти-

пов. Для некоторых критических программистских задач такие усилия могут быть оправданы, но для

каждодневного программирования они почти наверняка чрезмерны.

Тем не менее, было несколько попыток ввести зависимые типы в проекты практических языков про-

граммирования, в том числе Russell (Donahue and Demers 1985; Hook 1984), Cayenne (Augustsson 1998),

Зависимый ML (Xi and Pfenning 1998, 1999), Язык Ассемблера с Зависимыми Типами (Xi and Harper

2001), а также типы форм Джея и Секанины (Jay and Sekanina). В этих языках имеется тенденция

ограничивать мощность зависимых типов различными способами. В результате получаются системы,

более управляемые с вычислительной точки зрения, и для них легче автоматизировать проверку типов.

Например, в языках Си и др. зависимые типы используются только для уничтожения проверок выхода

за границы массива во время выполнения; в этих языках задачи «доказательства теорем», возникаю-

щие при проверке типов, представляют собой всего лишь системы линейных ограничений, и для них

существуют хорошие автоматизированные методы решения.

Одна из областей, где зависимые типы давно влияют на языки программирования — разработка си-

стем модулей, включающая механизмы, отслеживающие разделение межмодульных зависимостей. В

этой области классическими являются Pebble (Burstall and Lampson 1984), работы Маккуина (MacQueen

1986), Митчелла и Харпера (Mitchell and Harper 1988), Харпера и др. (Harper et al. 1990) и Харпера

и Стоуна (Harper and Stone 2000). В последнее время стал использоваться технический механизм од-

ноэлементных видов, при котором зависимость между модулями отслеживается на уровне видов, а не

типов (напр., Stone and Harper 2000; Crary 2000; см. также Hayashi 1991; Aspinall 1994).

rev. 104

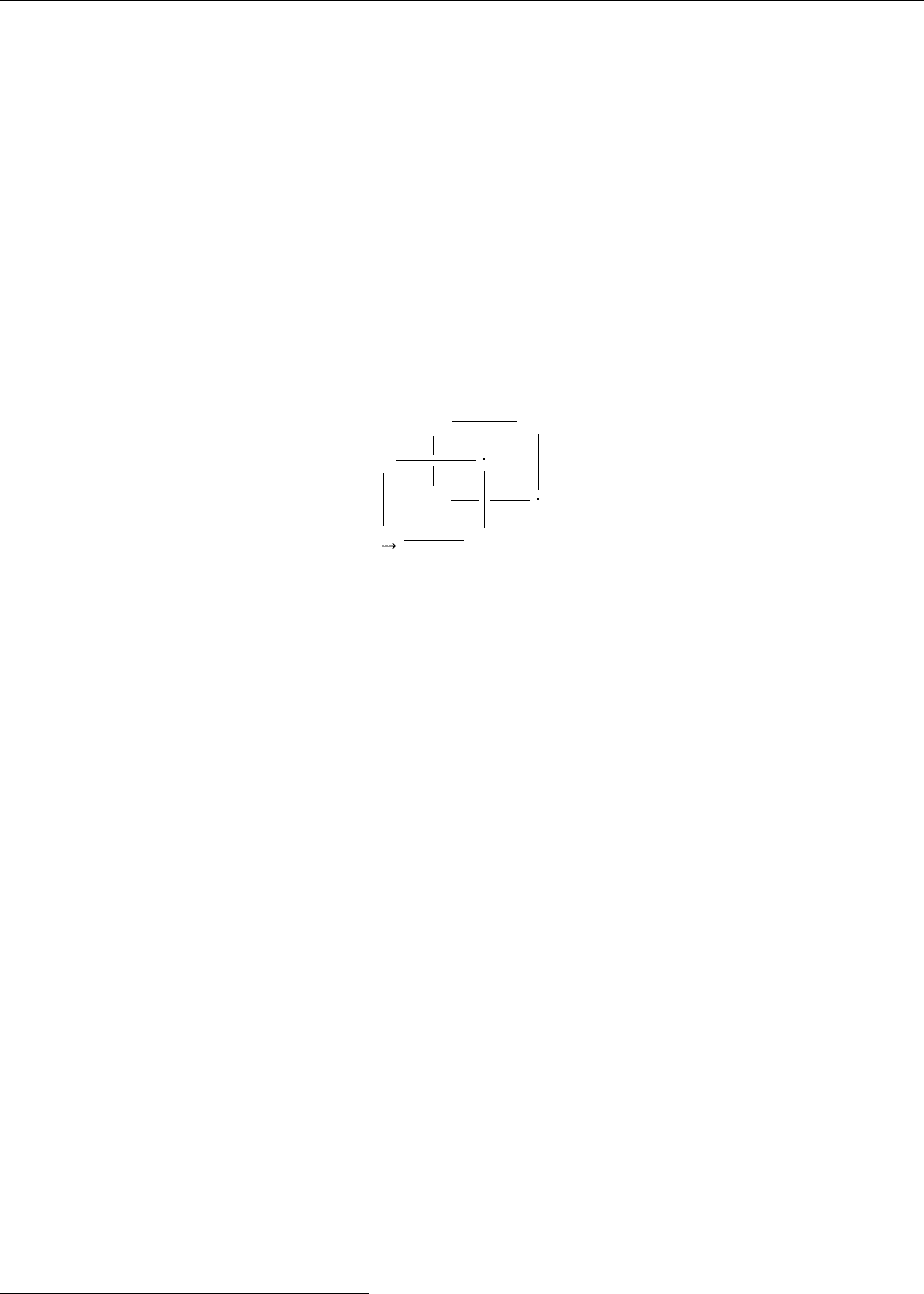
30.5. Идем дальше: зависимые типы 357

Сочетание зависимых типов и наследования впервые рассмотрено Карделли (Cardelli 1988b), а за-

тем развито и обобщено Аспиналлом (Aspinall 1994), Пфеннингом (Pfenning 1993b), Аспиналлом и

Компаньони (Aspinall and Compagnoni 2001), Ченом и Лонго (Chen and Longo 2006) и Званенбургом

(Zwanenburg 1999).

Еще одно важное приложение зависимых типов в информатике состоит в построении систем содей-

ствия доказательству и программ для автоматического доказательства теорем. В частности, простые

системы типов, содержащие зависимые типы, часто называют логическими конструкциями. Наибо-

лее известны среди них чистое простое типизированное лямбда-исчисление с зависимыми типами, LF

(Harper, Honsell and Plotkin 1992). LF и родственные ему системы, в частности исчисление конструкций

(Coquand and Huet 1988; Luo 1994), послужили основой для долгой традиции сред доказательства тео-

рем, включая AutoMath (de Bruijn 1980), NuPRL (Constable et al. 1986), LEGO (Luo and Pollack 1992;

Pollack 1994), Coq (Barras et al. 1997), ALF (Magnusson and Nordstr¨om 1994) и ELF (Pfenning 1994).

Более подробный обзор можно найти у Пфеннинга (Pfenning 1996).

Четыре формы абстракции, рассмотренные ранее в этом разделе, можно изящно изобразить на

следующей диаграмме, известной как куб Барендрегта:

Все системы в этом кубе включают обыкновенную абстракцию термов. Верхняя грань представляет

системы с полиморфизмом (семействами термов, проиндексированных типами), дальняя грань — си-

стемы с операторами над типами, а правая грань — системы с зависимыми типами. В правом дальнем

углу находится исчисление конструкций (calculus of constructions, CC), содержащее все четыре формы

абстракции. Еще один упомянутый нами ранее угол – LF, простое типизированное лямбда-исчисление с

зависимыми типами. Все системы куба Барендрегта, а также многие другие, могут быть представлены

как частные случаи общей конструкции систем чистых типов (Terlouw 1989; Berardi 1988; Barendregt

1991, 1992; Jutting, McKinna and Pollack 1994; McKinna and Pollack 1993; Pollack 1994).

Барендрегт (Barendregt 1991) назвал ее лямбда-куб .

rev. 104

358 30.5. Идем дальше: зависимые типы

Расширяет λ

(29.1) и Систему F (23.1)

Синтаксис

t ::= термы:

x переменная

λx:T.t абстракция

t t применение

λX ::K .t абстракция типа

t [T] применение типа

v ::= значения:

λx:T.t значение-абстракция

λX ::K .t значение-абстракция типа

T ::= типы:

X типовая переменная

T T тип функций

X ::K .T универсальный тип

λX::K.T абстракция оператора

T T применение оператора

Γ ::= контексты:

пустой контекст

Γ, x:T связывание термовой переменной

Γ, X::K связывание типовой переменной

K ::= виды:

* вид простых типов

K K вид операторов

Вычисление t t’

(E-App1)

(E-App2)

(λ x:T

) v

x v

(E-AppAbs)

] t

]

(E-TApp)

(λX ::K

) [T

] X T

(T-TappTabs)

Присвоение видов Γ T :: K

X::K Γ

Γ X :: K

(K-TVar)

Γ, X::K

:: K

Γ λX::K

:: K

(K-Abs)

Γ T

:: K

Γ T

:: K

Γ T

:: K

(K-App)

Γ T

:: * Γ T

:: *

Γ T

:: *

(K-Arrow)

Γ, X::K

::*

Γ X::K

:: *

(K-All)

см. на след. странице. . .

Эквивалентность типов S T

T T (Q-Refl)

T S

S T

(Q-Symm)

S U U T

S T

(Q-Trans)

(Q-Arrow)

X::K

(Q-All)

λX::K

(Q-Abs)

(Q-App)

(λX::K

) T

X T

(Q-AppAbs)

Типизация Γ t : T

x : T Γ

Γ x : T

(T-Var)

Γ T

:: * Γ, x:T

Γ λx:T

: T

(T-Abs)

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Γ, X ::K

: T

Γ λX ::K

: X ::K

(T-TAbs)

Γ t

: X ::K

Γ T

:: K

Γ t

] : X T

X.T

(T-TApp)

Γ t : S S T Γ T :: *

Γ t : T

(T-Eq)

Рис. 30.1. Полиморфное лямбда-исчисление высших порядков (F

)

rev. 104

30.5. Идем дальше: зависимые типы 359

Расширяет F

(30.1) и 24.1

Новые синтаксические формы

T ::= . . . типы:

{ X ::K ,T} экзистенциальный тип

Новые правила вычисления t t

let {X,x}=({*T

} as T

) in t

X T

x v

(E-UnpackPack)

{*T

} as T

{*T

} as T

(E-Pack)

Новые правила присвоения видов Γ T :: K

Γ, X::K

:: *

Γ { X::K

} :: *

(K-Some)

Новые правила эквивалентности типов S T

{ X::K

} { X::K

}

(Q-Some)

Новые правила типизации Γ t : T

Γ t

: X U T

Γ { X::K

} :: *

Γ {*U,t

} as { X ::K

} : { X ::K

}

(T-Pack)

Γ t

: { X ::K

} Γ, X ::K

, x:T

: T

Γ let {X,x}=t

in t

: T

(T-Unpack)

Рис. 30.2. Экзистенциальные типы высших порядков

Параллельная редукция S V T

T V T QR-Refl

V T

QR-Arrow

V T

X::K

V X::K

QR-All

V T

λX::K

V λX::K

QR-Abs

V T

QR-App

V T

(λX::K

) S

V X T

QR-AppAbs

Рис. 30.3. Параллельная редукция на типах

rev. 104

360 30.5. Идем дальше: зависимые типы

rev. 104