Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

23.11. Дополнительные замечания 281

Говоря о терминологии, почему «предикативный» и «импредикативный»? Отброшенной

банальностью о классах и условиях членства в них для нас было то, что, по выражению

Рассела, всякий предикат определяет класс; затем он приспосабливается к отказу от этой

банальности, отказывая в звании предиката таким условиям членства, которые более не рас-

сматриваются как определяющие классы. Так что «предикативный» не относилось ни к част-

ному иерархическому подходу, ни к метафоре последовательного построения; это было про-

сто конкретное предложение Рассела и Пуанкаре, какие условия членства считать продук-

тивными при образовании классов, или «предикативными». Однако вскоре хвост стал вилять

собакой. Сегодня предикативная теория множеств — это конструктивная теория, а импреди-

кативное определение понимается строго как объяснено в предыдущем абзаце,независимо от

того, какие условия членства мы предпочитаем рассматривать как определяющие классы.

23.11. Дополнительные замечания

Дополнительную библиографию по Системе F можно найти во вводной статье Рейнольдса (Reynolds

1990) и в его же «Теориях языков программирования» (Theories of Programming Languages, Reynolds

1998b).

rev. 104

282 23.11. Дополнительные замечания

rev. 104

Глава 24

Экзистенциальные типы

После того, как мы исследовали роль кванторов общности в системах типов (Глава 23), естественно

задаться вопросом, могут ли быть полезны в программировании кванторы существования. И действи-

тельно, кванторы существования оказываются изящной основой для абстракции данных и сокрытия

информации.

24.1. Мотивация

Экзистенциальные типы концептуально не сложнее универсальных (на самом деле, в §24.3 мы

увидим, что экзистенциальные типы без труда можно выразить в терминах универсальных). Одна-

ко формы для введения и удаления экзистенциальных типов синтаксически несколько тяжеловеснее,

чем простые абстракция и применение типов, связанные с универсальными типами, и для некоторых

эти формы поначалу кажутся непонятными. Следующие интуитивные соображения могут помочь Вам

побыстрее проскочить эту стадию.

Универсальные типы из Главы 23 могут рассматриваться с двух различных точек зрения. Логиче-

ская интуиция говорит нам, что элемент типа X.T является значением, которое имеет тип X S T

при любом выборе S. Эта интуиция соответствует взгляду на поведение со стиранием типов: например,

полиморфная функция тождества λX.λx:X.x при стирании дает бестиповую функцию тождества λx.x,

переводящую аргумент любого типа S в результат того же типа. Напротив, более операционная инту-

иция состоит в том, что элементом λX.T является функция, переводящая тип S в специализированный

терм типа X S T. Эта интуиция соответствует нашему определению Системы F из Главы 23, согласно

которому редукция применения типов представляет собой отдельный шаг вычисления.

Подобным образом, есть две возможных точки зрения на экзистенциальный тип, записываемый как

{ X,T}. Логическая интуиция говорит, что элементом { X,T} является значение типа X S T для

какого-то типа S. С другой стороны, операционная интуиция говорит, что элементом { X,T} служит

пара, записываемая как {*S,t}, состоящая из типа S и терма t, имеющего тип X S T.

В этой главе мы будем особо подчеркивать операционный взгляд на экзистенциальные типы, по-

скольку он предоставляет более близкую аналогию между экзистенциальными типами и модулями и

абстрактными типами данных в языках программирования. Наш конкретный синтаксис для экзистен-

циальных типов отражает эту аналогию: мы пишем { X,T} — и фигурные скобки подчеркивают, что

значение экзистенциального типа представляет собой разновидность кортежа, — вместо более стан-

дартной нотации X.T.

Чтобы понять экзистенциальные типы, нужно знать две вещи: как строить (или, в терминологии

§9.4, вводить) элементы этих типов, и как эти значения использовать (или удалять) в вычислениях.

Значение экзистенциального типа вводится путем построения пары из типа и терма, записываемой

{*S,t}.

Полезное интуитивное объяснение — считать значение {*S,t} типа { X,T} простой формой

На протяжении большей части этой главы изучается Система F (Рис. 23.1) с экзистенциальными типами (Рис. 24.1).

В примерах используются также записи (11.7) и числа (8.2). Соответствующий интерпретатор на OCaml называется

fullpoly.

Мы помечаем компоненту-тип такой пары значком *, чтобы четче отделить ее от обыкновенных кортежей-термов

283

284 24.1. Мотивация

пакета или модуля с одной (скрытой) компонентой-типом и одной компонентой-термом.

Тип S часто

называют скрытым типом-представлением, или, иногда, чтобы подчеркнуть связь с логикой (см. §9.4),

типом-свидетелем пакета. Например, пакет p {*Nat, {a=5, f=λx:Nat. succ(x)}} имеет экзистен-

циальный тип { X, {a:X,f:X X}}. Типовая компонента p равняется Nat, а компонентой-значением

служит запись, содержащая поле a типа X и поле f типа X X, для некоторого X (а именно Nat).

Тот же пакет p имеет также тип { X,{a:X, f:X Nat}}, поскольку его правая компонента является

записью с полями a и f типов X и X Nat, для некоторого X (а именно Nat). Этот пример показывает, что

в общем случае программа проверки типов не может принять автоматическое решение, какому типу

принадлежит данный пакет: программист должен указывать, какой тип имеется в виду. Простейший

способ этого добиться — просто добавить аннотацию к каждому пакету с явным указанием его типа.

Таким образом, полная форма введения для экзистенциальных значений будет выглядеть так:

p = {* Nat , {a =5 , f =λx: Nat . succ ( x )}} as { X , {a:X , f :X ->X }};

p : { X , {a :X , f :X ->X }}

или (тот же пакет с другим типом):

p = {* Nat , {a =5 , f =λx: Nat . succ ( x )}} as { X , {a:X , f :X -> Nat }};

p : { X , {a :X , f :X -> Nat }}

Аннотация типа, вводимая ключевым словом as, подобна конструкции приписывания типа, введенной

в §11.4. Приписывание позволяет пометить любой терм типом, который он должен иметь. В сущности,

мы включаем одно приписывание как часть конкретного синтаксиса конструкции создания пакета.

Правило типизации для введения экзистенциального квантора таково:

Γ t

: X U T

Γ {*U,t

} as { X,T

} : { X,T

}

(T-Pack)

Следует заметить, что, согласно этому правилу, пакеты с различными типами представления могут

принадлежать одному и тому же экзистенциальному типу. Например:

p2 = {* Nat , 0} as { X ,X}

p2 : { X ,X}

p3 = {* Bool , true } as { X ,X}

p3 : { X ,X}

Или, в более полезном варианте,

p4 = {* Nat , { a=0 , f=λx : Nat . succ ( x )}} as { X , {a:X , f :X -> Nat }};

p4 : { X , { a:X , f:X - > Nat }}

p5 = {* Bool , {a= true , f=λx : Bool . 0}} as { X , { a:X , f:X -> Nat }};

p5 : { X , { a:X , f:X - > Nat }}

Упражнение 24.1.1 : Вот еще несколько вариаций на ту же тему:

(§11.7). Еще один распространенный способ записи для введения экзистенциального значения выглядит как pack X=S

with t.

Разумеется, нетрудно обобщить модули такого вида на случай с несколькими компонентами-типами или

компонентами-термами, но давайте пока оставим по одной, чтобы нотация оставалась обозримой. Эффекта несколь-

ких компонент-типов можно добиться вложением нескольких экзистенциальных типов с одной типовой переменной, а

эффект нескольких компонент-термов достигается, если в качестве правой компоненты использовать кортеж или запись:

{*S

, *S

, t

}

def

{*S

, {*S

, {t

, t

}}}

rev. 104

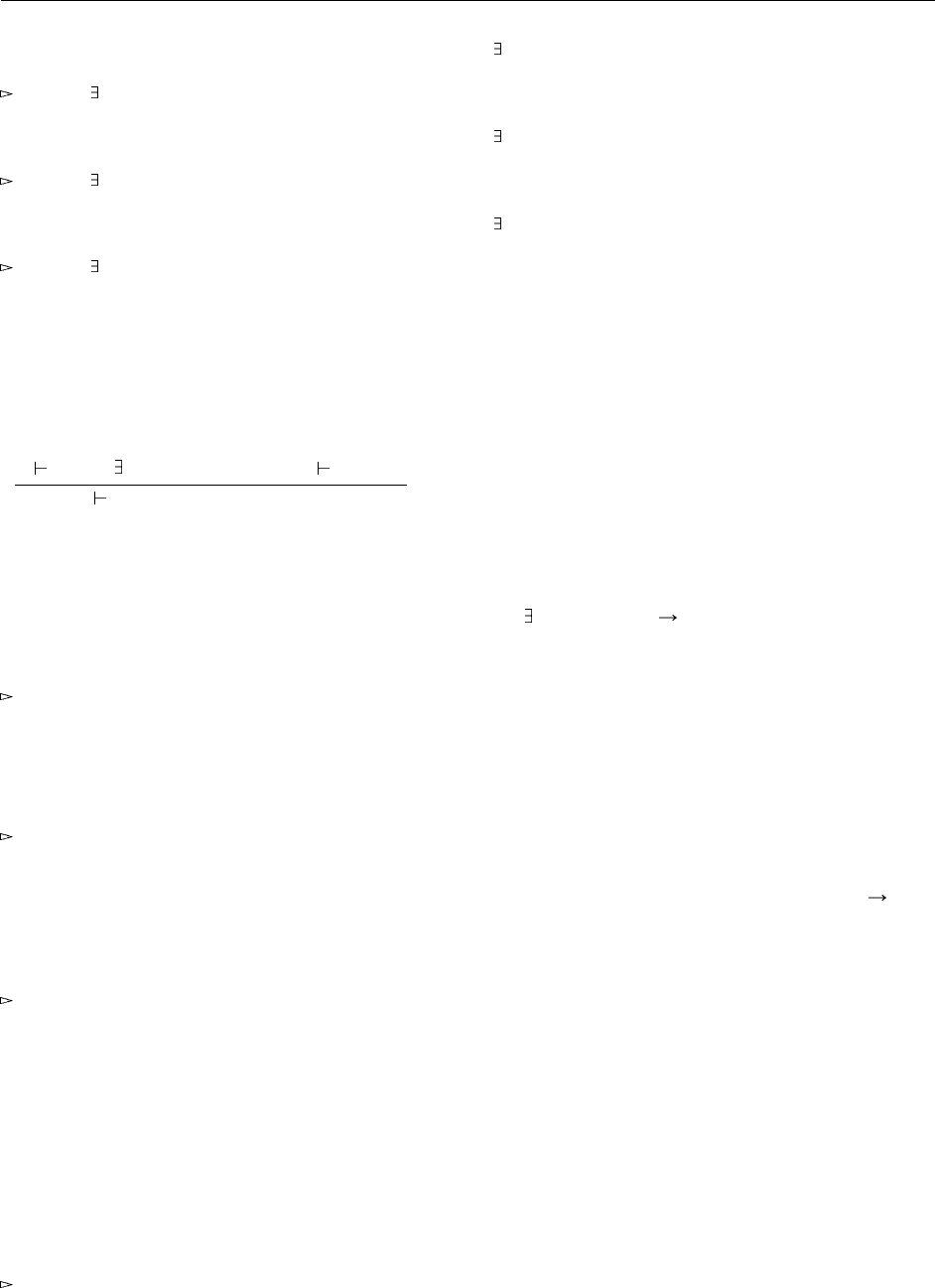
24.1. Мотивация 285

p6 = {* Nat , { a=0 , f=λx : Nat . succ ( x )}} as { X , {a:X , f :X ->X }};

p6 : { X , { a:X , f:X - >X }}

p7 = {* Nat , { a=0 , f=λx : Nat . succ ( x )}} as { X , {a:X , f :Nat -> X }};

p7 : { X , { a:X , f: Nat ->X }}

p8 = {* Nat , { a=0 , f=λx : Nat . succ ( x )}} as { X , {a:X , f :Nat -> Nat }};

p8 : { X , { a:X , f: Nat -> Nat }}

Почему они менее полезны, чем p4 и p5?

Аналогия с модулями также помогает нам понять конструкцию удаления экзистенциального кван-

тора. Если экзистенциальный пакет соответствует модулю, то удаление пакета подобно директиве open

или import: оно позволяет использовать содержимое модуля в каком-то другом месте программы, но

сохраняет природу типовой компоненты модуля абстрактной. Этого можно добиться связыванием че-

рез своего рода сопоставление с образцом:

Γ t

: { X,T

} Γ, X, x:T

: T

Γ let {X,x}=t

in t

: T

(T-Unpack)

А именно, если t

— выражение, при вычислении дающее экзистенциальный пакет, то мы можем

связать его типовую и термовую компоненты с переменными образца X и x, и использовать эти пе-

ременные при вычислении t

. (Часто также встречается такой конкретный синтаксис для удаления

экзистенциального квантора: open t

as {X,x} in t

Возьмем, например, вышеупомянутый пакет p4 типа { X, {a:X, f:X Nat}}. Выражение удаления

let {X ,x }= p4 in (x . f x . a);

1 : Nat

открывает p4 и использует поля его тела (x.f и x.a) при вычислении числового результата. В теле

формы удаления можно также упоминать типовую переменную X:

let {X ,x }= p4 in (λy : X. x.f y) x. a ;

1 : Nat

То, что тип представления пакета при проверке типов в теле остается абстрактным, означает, что

над x разрешены только те операции, которые обеспечивает ее «абстрактный тип» {a:X, f:X Nat}.

В частности, мы не можем использовать x.a как число:

let {X ,x }= p4 in succ ( x .a );

Ошибка: аргумент succ не является числом

Это ограничение осмысленно, поскольку, как мы видели выше, пакет с тем же самым экзистенциальным

типом, что у p4, может использовать в качестве типа представления не только Nat, но и Bool (а также

любой другой тип).

Есть еще один, менее очевидный, способ не пройти проверку типов для конструкции удаления эк-

зистенциального квантора. В правиле T-Unpack типовая переменная X присутствует в контексте, где

вычисляется тип t

, но отсутствует в контексте заключения правила. Это означает, что тип резуль-

тата T

не может содержать свободных вхождений X, поскольку иначе в заключении эти вхождения X

окажутся вне области видимости.

let {X ,x }= p in x . a ;

Ошибка: нарушение области видимости!

Этот вопрос обсуждается более подробно в §25.5.

rev. 104

286 24.2. Абстракция данных при помощи экзистенциальных типов

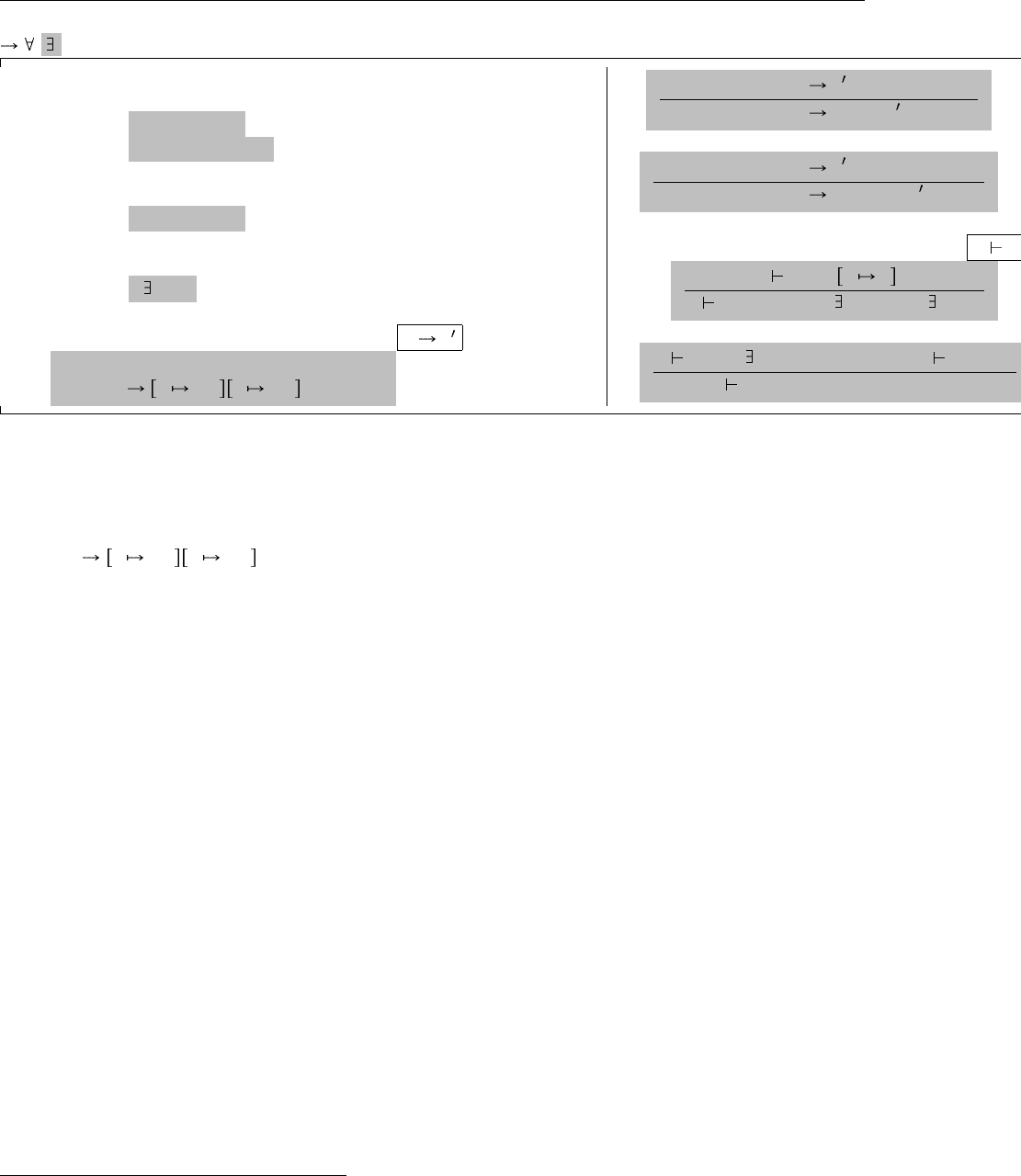
Расширяет Систему F (23.1)

Новые синтаксические формы

t ::= . . . термы:

{*T,t} as T упаковка

let X,x=t in t распаковка

v ::= . . . значения:

{*T,v} as T значение-пакет

T ::= . . . типы:

{ X,T} экзистенциальный тип

Новые правила вычисления t t

let {X,x}=({*T

} as T

) in t

X T

x v

(E-UnpackPack)

{*T

} as T

{*T

} as T

(E-Pack)

let X,x=t

in t

let X,x=t

in t

(E-Unpack)

Новые правила типизации Γ t : T

Γ t

: X U T

Γ {*U,t

} as { X,T

} : { X,T

}

(T-Pack)

Γ t

: { X,T

} Γ, X, x:T

: T

Γ let {X,x}=t

in t

: T

(T-Unpack)

Рис. 24.1. Экзистенциальные типы

Правило вычисления для экзистенциальной конструкции не представляет сложности:

let {X,x}=({*T

} as T

) in t

X T

x v

(E-UnpackPack)

Если первое подвыражение let сведено к конкретному пакету, то мы можем подставить компоненты

этого пакета вместо переменных X и x в теле t

. В терминах аналогии с модулями, это правило можно

рассматривать как шаг компоновки, когда символические имена (X и x), указывающие на компоненты

отдельно скомпилированого модуля, заменяются реальным содержимым этого модуля.

Поскольку в этом правиле все вхождения типовой переменной X подвергаются подстановке, получа-

ющаяся программа имеет доступ к конкретному содержимому пакета. Это еще один пример явления,

которое мы уже несколько раз наблюдали: по мере вычисления выражения могут становиться «более

типизированными» — в частности, неправильно типизированное выражение может перейти в правильно

типизированное.

Правила, определяющие расширение Системы F экзистенциальными типами, приведены на

Рис. 24.1.

24.2. Абстракция данных при помощи экзистенциальных типов

Во вводной главе (§1.2) мы говорили, что полезность систем типов далеко не исчерпывается обна-

ружением локальных ошибок программирования вроде 2+true: типы также оказывают весомую под-

держку при создании больших программ. В частности, типы помогают соблюдать не только абстракции,

встроенные в язык, но и абстракции, определенные программистом, — т. е., они не только защищают

машину от программы, но и части программы друг от друга.

В этом разделе рассматриваются два

различных стиля абстракции — классические абстрактные типы данных и объекты. Основой для

обсуждения обоих стилей служат экзистенциальные типы.

В отличие от кодирования объектов, рассмотренного нами в Главе 18, все примеры в этой гла-

ве являются чисто функциональными программами. Этот выбор сделан нами исключительно ради

удобства обсуждения: механизмы для обеспечения модульности и абстракции почти совершенно неза-

висимы от того, хранят ли определяемые абстракции изменяемое состояние или нет. (Упражнения

24.2.2 и 24.2.3 подчеркивают этот момент. В них разрабатываются императивные варианты некоторых

Справедливости ради, нужно сказать, что типы не единственный механизм для защиты абстракций, определеяемых

программистом. В бестиповых языках подобного эффекта можно достигнуть при помощи замыканий, объектов или

специализированных конструкций вроде единиц компиляции в MzScheme (Flatt and Felleisen 1998).

rev. 104

24.2. Абстракция данных при помощи экзистенциальных типов 287

чисто функциональных примеров из основного текста.) Причины, по которым мы предпочитаем чисто

функциональные примеры, таковы: (1) такой выбор ведет к тому, что наши примеры определяются в

рамках более простой и экономной формальной системы, и (2) при работе с чисто функциональны-

ми программами возникающие проблемы типизации иногда оказываются интереснее (а их решения,

соответственно, более показательными). Это получается потому, что при императивном программиро-

вании изменяемые переменные могут служить «побочным каналом связи», через который происходит

прямое общение удаленных друг от друга частей программы. В чисто функциональных программах

вся информация, передаваемая между различными частями программы, передается в виде аргументов

или результатов функций, и таким образом, «видима» для системы типов. Это в особенности верно

в случае объектов, и из-за этого нам придется отложить работу с некоторыми важными свойствами

языка (наследованием типов и реализаций) до Главы 32, когда в нашем распоряжении будут некоторые

более мощные, чем сейчас, механизмы теории типов.

24.2.1. Абстрактные типы данных

Традиционный абстрактный тип данных (или АТД ) состоит из (1) имени типа A, (2) типа кон-

кретного представления T, (3) реализации некоторых операций по созданию, извлечению информации

и манипулированию значениями типа T и (4) барьера абстракции, отделяющего представление и опе-

рации от внешнего мира. Внутри барьера абстракции элементы типа рассматриваются как конкретные

значения (типа T). Вне барьера они рассматриваются абстрактно, как значения типа A. Значения типа

A можно передавать из процедуры в процедуру, хранить в структурах данных и т. д., но нельзя напря-

мую обращаться к их представлению и изменять его — над A разрешены только те операции, которые

предоставляет АТД.

Вот, например, объявление абстрактного типа данных чисто функциональных счетчиков, записан-

ное на псевдокоде, близком к языкам Ada (U.S. Dept. of Defense 1980) или Clu (Liskov et al. 1981).

ADT count er =

type Counte r

representation Nat

sig n a ture

new : Counter ,

get : Counter - >Nat ,

inc : Counter - > Counter ;

oper a t i o n s

new = 1 ,

get = λi : Nat . i ,

inc = λi : Nat . succ ( i );

co unter . get ( coun ter . inc counte r . new );

Имя абстрактного типа Counter; его конкретным представлением является Nat. Реализации операций

работают с объектами Counter на конкретном уровне, как со значениями типа Nat: new — это просто

константа 1, операция inc представляет собой функцию-последователь; get — это функция тождества.

Раздел signature указывает, как эти операции должны использоваться извне; при этом некоторые эк-

земпляры Nat в их конкретных типах заменяются на Counter. Барьер абстракции огораживает участок

от ключевого слова ADT до закрывающей точки с запятой. В оставшейся части программы (т. е., в по-

следней ее строчке) связь между Counter и Nat разорвана, так что единственное, что можно сделать с

константой counter.new — это использовать ее как аргумент для counter.get или counter.inc.

Этот псевдокод почти посимвольно можно перевести в наше исчисление с экзистенциальными ти-

пами.Сначала мы создаем экзистенциальный пакет, содержащий внутренности АТД:

coun t e r A D T =

{* Nat ,

{ new = 1,

get = λi : Nat . i ,

inc = λi : Nat . succ ( i )}}

as { Counter ,

{ new : Counter ,

rev. 104

288 24.2. Абстракция данных при помощи экзистенциальных типов

get : Counter -> Nat ,

inc : Counter -> Count er }};

coun t e r A D T : { Counter ,

{ new : Counter , get : Counter - >Nat , inc : Counter -> Count er }}

Затем мы открываем пакет, вводя типовую переменную Counter как указание на скрытый тип пред-

ставления пакета и термовую переменную counter для доступа к операциям:

let { Counter , counter } = co u nterADT in

co unter . get ( coun ter . inc counte r . new );

2 : Nat

Версия с использованием экзистенциальных типов читается несколько труднее по сравнению с псевдо-

кодом, содержащим много синтаксического сахара, однако структура двух кусков кода идентична.

В общем случае тело конструкции let, открывающей экзистенциальный пакет, содержит всю остав-

шуюся часть программы:

let { Counter , cou nter } = <пакет counter> in

<остаток программы>

В этой оставшейстя части тип Counter может использоваться точно так же, как базовые типы, встро-

енные в язык. Можно определять функции, работающие со счетчиками:

let { Counter , cou nter }= c o u n terADT in

let add3 = λc: Coun ter . cou nter . inc ( counte r . inc ( co unter . inc c )) in

co unter . get ( add3 counte r . new );

4 : Nat

Можно даже определять новые абстрактные типы, чье представление включает в себя счетчики. На-

пример, следующая программа определяет АТД двухпозиционных переключателей, используя счетчик

в качестве (не слишком эффективного) типа представления:

let { Counte r . co unter } = co u n t e rADT in

let { FlipFlop , flipflo p } =

{* Counter ,

{ new = counte r . new ,

read = λc : Counter . iseven ( counter . get c),

to ggle = λc: Cou nter . cou nter . inc c ,

reset = λc : Counter . counter . new }}

as { FlipFlop ,

{ new : FlipFlop , read : FlipFlop - >Bool ,

to ggle : FlipFlop -> FlipFlop , reset : FlipFlop -> FlipFl op }} in

fli pflop . read ( fli p flop . togg le ( flipf l op . toggl e flipflop . new ));

false : Bool

Таким образом можно разбить большую программу на некоторое количество объявлений АТД, каждый

из которых использует типы и операции, предоставляемые предыдущими АТД, чтобы построить свои

типы и операции и упаковать их для следующих АТД в виде ясно и четко определенной абстракции.

Ключевое свойство сокрытия информации в таких случаях — независимость представлений. Мож-

но подставить другую реализацию АТД счетчика — скажем, такую, где в качестве внутреннего пред-

ставления используется запись с полем типа Nat, а не просто Nat,

coun t e r A D T =

{* x: Nat {} ,

{ new = {x =1} ,

get = λi :{ x: Nat }. i.x ,

rev. 104

24.2. Абстракция данных при помощи экзистенциальных типов 289

inc = λi :{ x: Nat }. {x = succ ( i . x )}}}

as { Counter ,

{ new : Counter , get : Counter -> Nat , inc : Counter - > Counter }};

coun t e r A D T : { Counter ,

{ new : Counter , get : Counter - >Nat , inc : Counter -> Count er }}

будучи совершенно уверенными, что вся программа останется правильно типизированной, поскольку

мы наверняка знаем, что оставшаяся часть программы никак не может обратиться к экземплярам

Counter иначе как через get и inc.

Опыт показывает, что стиль программирования, основанный на абстрактных типах данных, может

принести громадные улучшения в надежности и легкости сопровождения больших систем. Тому есть

несколько причин. Во-первых, такой стиль ограничивает область видимости изменений в программе.

Как мы только что видели, можно заменить одну реализацию АТД другой, возможно, меняя при этом

как тип представления, так и реализацию операций, никак не влияя на остальную программу, поскольку

правила типизации для экзистенциальных пакетов обеспечивают независимость остальной программы

от внутреннего представления АТД. Во-вторых, такой стиль помогает программистам ограничивать

зависимости между частями программы, делая сигнатуры АТД как можно меньше. Наконец, и может

быть, это самое важное, этот стиль заставляет программистов думать о проектировании абстракций.

Упражнение 24.2.1 Рекомендуется, : Используя приведенный нами пример в качестве об-

разца, определите абстрактный тип стеков чисел, с операциями new, push (поместить значение на

стек), top (вернуть значение на вершине стека), pop (вернуть новый стек с удаленной вершиной) и

isempty. Используйте в качестве представления тип List, введенный в Упражнении 23.4.3. Напи-

шите простую программу, которая создает стек, записывает в него два числа, и получает верхний

элемент стека. Лучше всего выполнять это упражнение интерактивно. Запустите интерпрета-

тор fullomega и скопируйте содержимое файла test.f (где определяется конструктор типов List

и связанные с ним операции) в начало собственного файла.

Упражнение 24.2.2 Рекомендуется, : Постройте АТД изменяемых счетчиков, используя ссы-

лочные ячейки, определенные в Главе 13. Пусть операция new будет не константой, а функцией, при-

нимающей аргумент типа Unit и возвращающей счетчик, а возвращаемый тип операции inc пусть

будет не Counter, а Unit. (Интерпретатор fullomega поддерживает как экзистенциальные типы,

так и ссылки.)

24.2.2. Экзистенциальные объекты

Идиома «упаковать, а затем открыть», которую мы видели в предыдущем подразделе, типична для

программирования с использованием экзистенциальных пакетов в качестве АТД. Пакет определеяет

абстрактный тип и связанные с ним операции, а мы открываем каждый пакет немедленно после его

создания, связывая при этом типовую переменную, обозначающую абстрактный тип, и открывая аб-

страктный доступ к операциям над АТД. В этом подразделе мы увидим, как простая разновидность

объектно-ориентированной абстракции данных может быть представлена в виде другой программист-

ской идиомы, основанной на экзистенциальных типах. Эта объектная модель далее разрабатывается в

Главе 32.

Мы снова будем использовать в качестве основного примера простые счетчики, как мы делали и в

случае с экзистенциальными АТД, и в наших предыдущих опытах с объектами в Главах 18 и 19. Мы

снова выбираем чисто функциональный стиль, так что посылка сообщения inc объекту не изменяет

его внутреннее состояние, а возвращает новый счетчик с увеличенным внутренним состоянием.

Объект-счетчик состоит из двух основных компонент: числа, являющегося внутренним состоянием

счетчика, и пары методов, get и inc, используемых для работы с этим состоянием. Нам также нужно

добиться того, чтобы единственным способом обращения к состоянию или его изменения был вызов

одного из этих двух методов. Этого можно добиться, если завернуть состояние и методы в экзистенци-

альный пакет и абстрагироваться от типа состояния. Например, объект-счетчик, имеющий значение 5,

можно записать как

rev. 104

290 24.2. Абстракция данных при помощи экзистенциальных типов

c = {* Nat ,

{ state = 5,

me thods = { get = λx: Nat . x ,

inc = λx : Nat . succ ( x )}}

as Counter ;

где

Co unter = { X , { state :X , methods : { get :X ->Nat , inc :X ->X }}};

Чтобы вызвать метод объекта-счетчика, мы открываем экзистенциальный пакет и применяем соот-

ветствующий элемент его поля methods к полю state. Например, чтобы получить текущее значение c,

мы можем написать:

let {X , body } = c in body . methods . get ( body . state );

5 : Nat

Обобщая, мы можем написать маленькую функцию, «посылающую сообщение get» любому счетчику:

se ndget = λc: Counter .

let {X , body } = c in

body . m ethods . get ( body . state );

se ndget : Counte r -> Nat

Вызов метода inc для объекта-счетчика выглядит несколько сложнее. Если мы просто повторим код

для get, программа проверки типов выдаст ошибку:

let {X , body } = c in body . methods . inc ( body . state );

Ошибка: нарушение области видимости!

поскольку типовая переменная X оказывается несвязанной в типе тела let. В самом деле, написанный

нами код интуитивного смысла тоже не имеет, поскольку результатом метода inc является голое внут-

реннее состояние, а не объект. Чтобы удовлетворить одновременно процедуру проверки типов и свои

неформальные понятия о том, к чему должен приводить вызов inc, мы должны взять новопорожден-

ное внутреннее состояние и упаковать его в виде объекта-счетчика, используя при этом ту же самую

запись с методами и тот же тип внутреннего состояния, как в исходном объекте:

c1 = let {X , body } = c in

{*X ,

{ state = body . m ethods . inc ( body . state ) ,

me thods = body . metho ds }}

as Counter ;

В общем случае, чтобы «послать счетчику сообщение inc», можно написать

se ndinc = λc: Counter .

let {X , body } = c in

{*X ,

{ state = body . m ethods . inc ( body . state ) ,

me thods = body . metho ds }}

as Counter ;

se ndinc : Counte r -> C ounter

Более сложные операции над счетчиками можно построить на основе двух имеющихся базовых опера-

ций:

add3 = λc : C ounter . sendinc ( s endinc ( sendinc c ));

add3 : Cou nter -> Co unter

rev. 104