Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

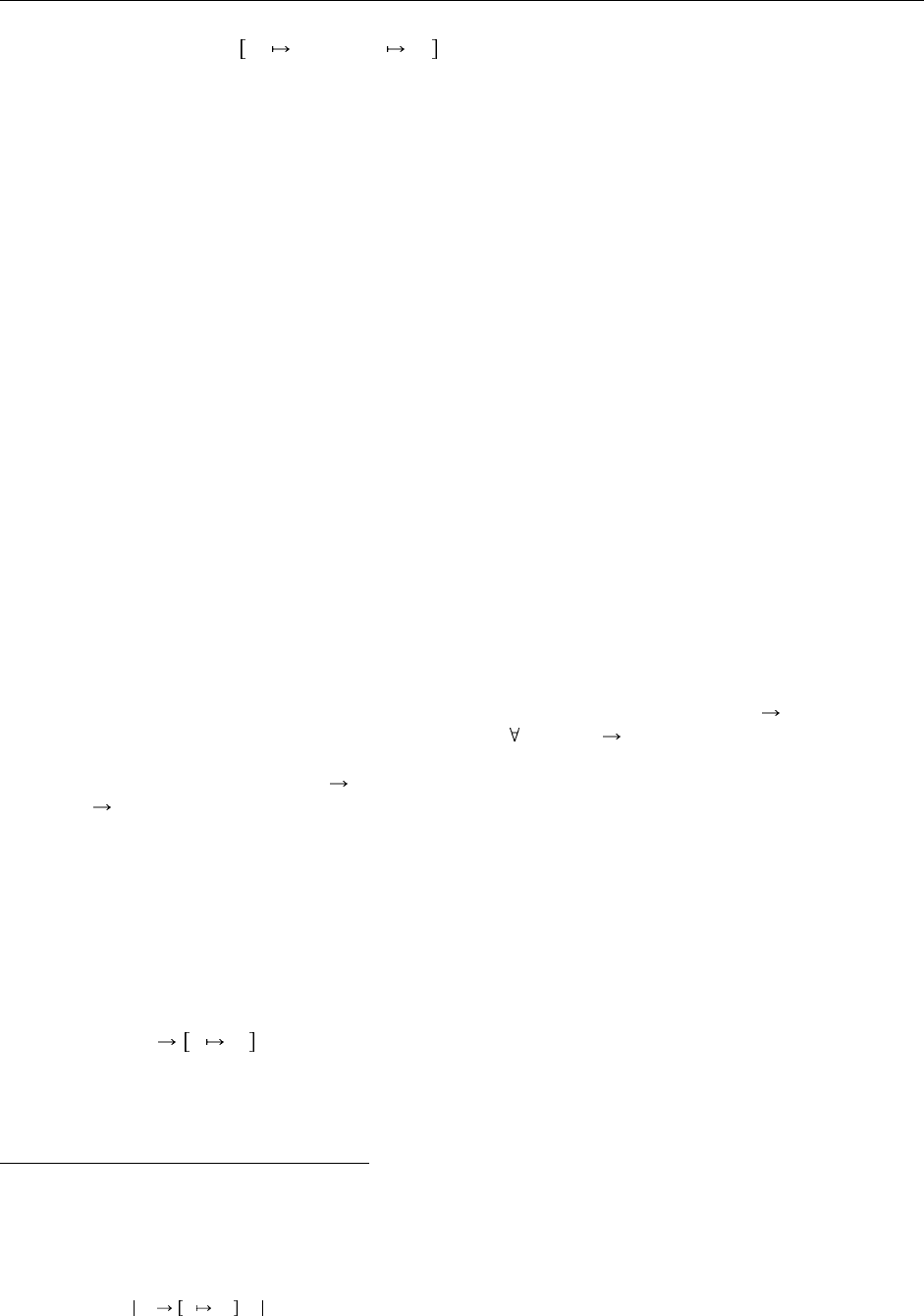
22.7. Полиморфизм через LET 261

схему типа, получая X

, . . . , X

. Это последнее выражение мы используем как тип

Этот алгоритм намного эффективнее, чем простой подход с подстановкой в выражения let перед

проверкой типов. Десятилетия использования показали, что на практике он «по существу линеен»

относительно размера входной программы. И большой неожиданностью было, когда Кфури, Тюрин и

Ужичин (Kfoury, Tiuryn and Urzyczyn 1990) и, независимо от них, Мейрсон (Mairson 1990) показали,

что в наихудшем случае сложность алгоритма по-прежнему экспоненциальна! Построенный ими пример

содержит нагромождение let в связываемой позиции других let — а не в телах, где вложенные let

обычно встречается. В результате получаются выражения, чьи типы растут экспоненциально быстрее,

чем сами выражения. Например, следующая программа на OCaml, приводимая Мейрсоном (Mairson

1990), правильно типизирована, но проверка типов в ней занимает весьма долгое время:

let f

= fun x -> (x ,x) in

let f

= fun y -> f

y) in

let f

= fun y -> f

y) in

let f

= fun y -> f

y) in

let f

= fun y -> f

y) in

let f

= fun y -> f

y) in

( fun z -> z)

Чтобы понять, почему это так, попробуйте ввести f

, f

, и т. д. по одному в OCaml-овскую команд-

ную строку. Дальнейшее обсуждение можно найти у Кфури, Тюрина и Ужичина (Kfoury, Tiuryn and

Urzyczyn 1994).

Последнее, что следует упомянуть — при проектировании языков с полиморфизмом через let сле-

дует осторожно относиться к взаимодействию полиморфизма и конструкций с побочными эффектами

вроде изменяемых ячеек памяти. Простой пример может проиллюстрировать эту опасность:

let r = ref (λx . x ) in

(r :=(λx: Nat . succ x );

(! r) true );

По приведенному выше алгоритму, правая часть let получает главный тип Ref (X X); поскольку X

нигде больше не встречается, этот тип обобщается до X.Ref (X X), и эту схему мы присваиваем

переменной r, добавляя ее в контекст. При проверке типов для присваивания во второй строке эта

схема конкретизируется до Ref (Nat Nat). При проверке третьей строки она же конкретизируется до

Ref (Bool Bool). Однако такая типизация некорректна, поскольку при исполнении терма произойдет

попытка применить операцию succ к значению true.

Проблема состоит в том, что правила типизации оказались рассинхронизированы с правилами вы-

числения. Правила типизации, введенные в этом разделе, говорят, что как только мы видим выражение

let, мы должны немедленно вставить его правую часть в тело. Однако правила вычисления говорят,

что эту подастановку можно производить только после того, как правая часть сведена к значению. Пра-

вила типизации видят два употребления конструктора ref и анализируют их в разных окружениях,

однако при вычислении выделяется только одна ref-ячейка.

Исправить расхождение можно двумя способами — изменив вычисление или типизацию. В первом

случае

правило вычисления для let превратится в

let x=t

in t

x t

(E-Let)

С такой стратегией первый шаг при вычислении нашего опасного примера заменит r его определением,

и получится

( ref (λx . x )) := (λx: Nat . succ x ) in

(!( ref (λx. x ))) true ;

Различие между лямбда-абстракцией, явно аннотированной типовой переменной, и неаннотированной абстракцией,

которой алгоритм порождения ограничений приписывает новую переменную, потеряет свое значение, когда мы введем

обобщение и конкретизацию. В обоих случаях связываемое выражение в let получает тип, включающий в себя перемен-

ную. Эта переменная подвергается обобщению, прежде чем алгоритм вносит ее в контекст, и заменяется новой переменной

при каждой конкретизации.

Строго говоря, в этом правиле нужно упомянуть состояние памяти, как это было сделано в Главе 13, поскольку

речь идет о языке со ссылками:

let x=t

in t

µ x t

µ (E-Let)

rev. 104

262 22.8. Дополнительные замечания

что совершенно безопасно! В первой строке создается ячейка, инициализируемая функцией тождества,

а затем в нее записывается (λx:Nat. succ x). Во второй строке создается другая ячейка, содержащая

функцию тождества, ее содержимое извлекается и применяется к аргументу true. Однако этот пример

показывает также, что изменение правил вычисления с целью соответствовать правилам типизации

дает нам язык с достаточно странной семантикой, которая уже не соответствует нашим интуитивным

понятиям о порядке вычислений по вызову. (Императивные языки с другими стратегиями вычисления

существуют (Augustsson 1984), но они не смогли завоевать популярность, поскольку в них трудно понять

порядок побочных эффектов во время исполнения и управлять им.)

Лучше будет изменить правило типизации, чтобы оно соответствовало правилу вычисления. К сча-

стью, это не представляет труда: мы просто добавляем ограничение (его часто называют ограничение

на значения), которое говорит, что связываение через let может рассматриваться как полиморфное

— т. е., его переменные могут подвергаться обобщению, — только в случае, если его правая сторона

является синтаксическим значением. Это означает, что в нашем опасном примере тип, присваиваемый

переменной r, когда она добавляется в контекст, равен X X, а не X.X X. Ограничения, накладыва-

емые второй строкой, заставляют X быть равным Nat, и из-за этого проверка типов в третьей строке

потерпит неудачу, поскольку Nat и Bool не унифицируются.

Ограничение на значения решает нашу проблему с типовой безопасностью ценой некоторой потери

выразительности: у нас больше не получится писать программы, в которых правая сторона выражения

let выполняет некоторое интересное вычисление, и при этом ей присваивается полиморфная схема

типа. Удивительно то, что это ограничение почти не влияет на практическое программирование. Райт

(Wright 1995) показал это, проанализировав огромный массив кода, написанного на диалекте ML —

Стандартном ML в версии 1990 года (Milner, Tofte and Harper 1990), — предоставлявшем более гибкое

правило типизации для let, основанное на слабых типовых переменных, и заметив, что, кроме горстки

случаев, правые части let все равно являлись значениями. Наблюдение Райта более или менее закрыло

дискуссию, и с тех пор все основные языки с полиморфизмом в стиле ML соблюдают ограничение на

значения.

Упражнение 22.7.1 : Реализуйте алгоритм, наметки которого приведены в этом разделе.

22.8. Дополнительные замечания

Понятие главного типа в лямбда-исчислении восходит по крайней мере к работам Карри 50-х годов

(Curry and Feys 1958). Алгоритм вычисления главных типов на основе идей Карри был построен Хиндли

(Hindley 1968); подобные алгоритмы были независимо обнаружены Моррисом (Morris 1968) и Милнером

(Milner 1978). В мире пропозициональной логики эти идеи существовали еще раньше: возможно, у

Тарского в 1920-х, и определенно у братьев Мередит в 1950-е (Lemmon, Meredith, Meredith, Prior and

Thomas 1957); первая их компьютерная реализация была осуществлена Дэвидом Мередитом в 1957

году. Дополнительные исторические сведения о главных типах можно найти у Хиндли (Hindley 1997).

Унификация (Robinson 1971) играет ключевую роль во многих областях информатики. Подробные

введения можно найти, например, у Баадера и Нипкова (Baader and Nipkow 1998), Баадера и Зикмана

(Baader and Siekmann 1994), и у Лассе и Плоткина (Lassez and Plotkin 1991).

Полиморфизм через let в стиле ML был впервые описан Милнером (Milner 1978). Было предложе-

но несколько алгоритмов реконструкции типов, из которых наиболее известен Алгоритм W Дамаса и

Милнера (Damas and Milner 1982; см. также Lee and Yi 1998). Основное отличие Алгоритма W от при-

веденного нами в этой главе состоит в том, что Алгоритм W приспособлен для «чистой реконструкции

типов» — присвоения типов исходно совершенно нетипизированным термам, — в то время как у нас

происходит одновременно реконструкция и проверка типов, а термы могут содержать явные аннотации,

где могут (но не обязательно) встречаться переменные. Это усложняет наше описание с технической

точки зрения (особенно доказательство полноты в Теореме 22.3.7, где нам приходится заботиться, чтобы

переменные, введенные программистом, отличались от тех, которые появляются в результате правил

порождения ограничений), однако такое изложение лучше сочетается с исчислениями из других глав

книги.

Классическая статья Карделли (Cardelli 1987) перечисляет несколько вопросов, возникающих при

реализации алгоритмов. Кроме того, описание алгоритмов реконструкции типов можно найти у Аппеля

rev. 104

22.8. Дополнительные замечания 263

(Appel 1998), Ахо и пр. (Aho et al. 1986), и у Рида (Reade 1989). Чрезвычайно изящное изложение

базовой системы, называемой мини-ML (Clement, Despeyroux, Despeyroux and Kahn 1986) часто служит

основой для технических рассуждений. Тюрин (Tiuryn 1990) рассматривает широкий спектр проблем

в реконструкции типов.

Главные типы не следует смешивать с родственным понятием главной типизации. Разница состоит

в том, что при вычислении главного типа контекст Γ и терм t рассматриваются как входы алгоритма, а

главный тип T служит его выходом. Алгоритм для вычисления главной типизации принимает на входе

только t, а на выходе выдает как Γ, так и T — т. е., он вычисляет минимальные предположения о

типовых переменных в t. Главные типизации оказываются полезны при раздельной компиляции и «оп-

тимальной перекомпиляции», для пошагового вывода типов и поиска ошибок типизации. К сожалению,

во многих языках, включая ML, имеются главные типы, но не главные типизации. См. (Jim 1996).

Полиморфизм в стиле ML, сочетая мощность и простоту, оказывается «наилучшим компромиссом»

в пространстве возможных языковых проектов; его смешение с другими мощными конструкциями ти-

пизации часто бывает весьма нетривиальным. Наибольший успех в этой области — изящное описание

реконструкции типов для записей, предложенное Вандом (Wand 1987) и развитое в работах Ванда

(Wand 1988, 1989b), Реми (R´emy 1989, 1990, 1992a, 1992b, 1998) и многих других. Идея состоит в

том, чтобы ввести новую разновидность переменных, переменные строк, которые имеют значением не

типы, а целые «строки», состоящие из меток и связанных с ними типов. Для решения множеств огра-

ничений, связанных с переменными строк, используется простая форма эквациональной унификации.

См. Упражнение 22.5.6. Гарриге (Garrigue 1994) и другие разработали подобные методы для вариант-

ных типов. Эти методы были распространены на общие понятия классов типов (Kaes 1988; Wadler and

Blott 1989), типов ограничений (Odersky, Sulzmann and Wehr 1999) и специфицированных типов (Jones

1994b,a), которые лежат в основе системы классов типов в языке Haskell (Hall et al. 1996; Hudak et al.

1992; Thopmson 1999); подобные идеи встречаются также в Mercury (Somogyi, Henderson and Conway

1996) и Clean (Plasmeijer 1998).

Уэллс (Wells 1994) показал, что задача реконструкции типов для более богатой формы импреди-

кативного полиморфизма неразрешима. Несколько разновидностей частичной реконструкции типов

для этой системы также оказываются неразрешимыми. В §23.6 и §23.8 приводится дополнительная

информация об этих результатах, и о том, как реконструкция типов в стиле ML сочетается с более

сильными формами вроде полиморфизма 2-го ранга.

Что касается сочетания реконструкции типов в стиле ML и наследования, были опубликованы

некоторые многообещающие результаты (Aiken and Wimmers 1993; Eifrig, Smith and Trifonov 1995;

Jagannathan and Wright 1995; Trifonov and Smith 1996; Odersky, Sulzmann and Wehr 1999; Flanagan and

Felleisen 1997; Pottier 1997), однако практические реализации пока не нашли широкого применения.

Было показано, что распространение реконструкции типов по ML на рекурсивные типы (Глава 20)

не представляет серьезных трудностей (Huet 1975, 1976). Единственное серьезное отличие от алгорит-

мов, приведенных в этой главе, касается определения унификации, где нужно опустить проверку на

вхождение (требующую отсутствия циклов). После того, как это сделано, чтобы по-прежнему гаран-

тировать завершение алгоритма, требуется изменить представление данных и обеспечить разделение

подструктур, например, через деструктивные обновления (возможно, циклических) структур, состоя-

щих из указателей. Такие представления обычны в высокопроизводительных реализациях языков.

С другой стороны, сочетание реконструкции типов с рекурсивно определенными термами ведет

к сложной проблеме, известной под названием полиморфная рекурсия. Простое (и не вызывающее

проблем) правило типизации для рекурсивных определений функций в ML говорит, что рекурсивная

функция может употребляться внутри своего опеределения только мономорфно (т. е., все рекурсив-

ные вызовы должны иметь одни и те же типы аргументов и результатов), в то время как в остальной

программе ее можно использовать полиморфно (с аргументами и результатами различных типов).

Майкрофт (Mycroft 1984) и Мейртенс (Meertens 1983) предложили полиморфное правило типизации,

позволяющее рекурсивным вызовам рекурсивной функции изнутри ее собственного тела конкрети-

зироваться различными типами. Было показано, что в этом расширении, известном как Исчисление

Милнера-Майкрофта, задача реконструкции типов неразрешима (Hengelin 1993, и, независимо от него,

Kfoury, Tiuryn and Urzyczyn 1993a); оба эти доказательства зависят от неразрешимости (неограничен-

ной) задачи полуунификации, которая была показана Кфури, Тюриным и Ужичиным (Kfoury, Tiuryn

and Urzyczyn 1993b).

rev. 104

264 22.8. Дополнительные замечания

rev. 104

Глава 23

Универсальные типы

В предыдущей главе мы рассмотрели простую разновидность полиморфизма через let, имеющегося

в ML. В этой главе мы изучаем более общую форму полиморфизма в рамках мощного исчисления,

известного как Система F .

23.1. Мотивация

Как мы упомянули в $22.7, в простом типизированном лямбда-исчислении можно написать беско-

нечное число «удваивающих» функций. . .

dou b l eNat = λf : Nat -> Nat . λx : Nat . f (f x );

dou b l eRcd = λf : Bool - > Bool . λx : Bool . f (f x );

dou b l eFun = λf :( Nat -> Nat ) - >( Nat - > Nat ). λx :Nat - > Nat . f ( f x );

Каждая из этих функций применима к своему типу аргумента, но поведение у них одинаковое (более

того, текст функций, помимо аннотаций типа, тоже одинаков). Если нам нужно применять операции

удвоения к различным типам аргументов внутри одной программы, нам придется написать отдельные

определения doubleT для каждого T. Такое программирование путем размножения текста нарушает

один из главных принципов разработки программ:

Принцип абстракции: Каждая существенная область функциональности в программе

должна быть реализована ровно в одном месте программного кода. Если различные участ-

ки кода реализуют похожую функциональность, как правило, имеет смысл слить их в один

участок, абстрагируя различающиеся части.

В данном случае различающиеся части — это типы! Таким образом, нам нужен способ абстрагировать

тип терма, а затем конкретизировать абстрактный терм аннотациями, нужными в данном частном

контексте употребления.

23.2. Разновидности полиморфизма

Системы типов, позволяющие использовать единый участок кода с различными типами, все вме-

сте известны как полиморфные (поли много, морф форма). В современных языках встречает-

ся несколько разновидностей полиморфизма (приводимая здесь классификация основана на работах

Стрейчи (Strachey 1967), а также Карделли и Вегнера (Cardelli and Wegner 1985)).

Параметрический полиморфизм, тема этой главы, позволяет давать участку кода «обоб-

щенный» тип, используя переменные вместо настоящих типов, а затем конкретизировать, за-

мещая переменные типами. Параметрические определения однородны: все экземпляры дан-

ного участка кода ведут себя одинаково.

На протяжении большей части этой главы изучается чистая Система F (Рис. 23.1); в примерах из §23.4 используются

расширения этой системы различными уже известными нам конструкциями. Соответствующий интерпретатор на OCaml

называется fullpoly. (Примеры с использованием пар и списков требуют интерпретатора fullomega.)

265

266 23.3. Система F

Наиболее мощной формой параметрического полиморфизма является импредикативный

полиморфизм, или полиморфизм первого класса. Именно он обсуждается в данной главе. На

практике больше распространен полиморфизм в стиле ML, то есть полиморфизм через let ,

ограниченный связываниями let верхнего уровня и запрещающий функции, где аргумента-

ми служат полиморфные значения. Взамен он предлагает удобную и естественную форму

реконструкции типов (Глава 22). Параметрический полиморфизм первого класса также по-

лучает распространение в языках программирования. Он служит техническим основанием

для мощной системы модулей в языках вроде ML (см. Harper and Stone 2000).

Специализированный полиморфизм, напротив, позволяет полиморфному значению де-

монстрировать различное поведение, будучи «рассмотренным» относительно разных типов.

Самый обычный пример специализированного полиморфизма — перегрузка, когда один и тот

же символ функции связан с различными реализациями; компилятор (или система времени

выполнения, в зависимости от того, имеем мы дело со статическим или динамическим раз-

решением перегрузки) выбирает подходящую реализацию для каждого случая применения

функции, исходя из типов ее аргументов.

Обобщением перегрузки функций служат мультиметоды в языках вроде CLOS (Bobrow

et al. 1988; Kiczales et al. 1991) и Cecil (Chambers 1992; Chambers and Leavens 1994). Этот

механизм был формализован в λ-&-исчислении Кастаньи, Гелли и Лонго (Castagna, Ghelli

and Longo 1995; ср. Castagna 1997).

Более мощная форма специализированного полиморфизма, интенсиональный полимор-

физм (Harper and Morrisett 1995; Crary, Weirich and Morrisett 1998), позволяет ограниченные

вычисления над типами во время выполнения. Интенсиональный полиморфизм лежит в ос-

нове некоторых сложных методов оптимизации для полиморфных языков, включая бесте-

говую сборку мусора, «неупакованные» аргументы функций, полиморфную сериализацию

и оптимизированные по памяти «плоские» структуры данных.

Еще более мощные формы специализированного полиморфизма можно получить на ос-

нове конструкции typecase, которая позволяет осуществлять произвольное сопоставление с

образцом информации о типах во время выполнения (Abadi, Cardelli, Pierce and R´emy 1995;

Abadi, Cardelli, Pierce and Plotkin 1991b; Henglein 1994; Leroy and Mauny 1991; Thatte 1990).

Конструкции вроде instanceof в Java можно рассматривать как ограниченную разновид-

ность typecaase.

Полиморфизм через наследование (Глава 15) присваивает много типов одному терму че-

рез правило включения, и позволяет нам избирательно «забывать» часть информации о

поведении терма.

Эти категории не являются взаимоисключающими: различниые формы полиморфизма могут смеши-

ваться в одном языке. Например, Стандартный ML имеет как параметрический полиморфизм, так и

протую перегрузку встренных арфиметических операций, но не наследование, а Java обладает насле-

дованием, перегрузкой и простым специализированным полиморфизмом (instanceof), но не имеет (на

момент написания книги) параметрического полиморфизма. Существует несколько предложений по

добавлению параметрического полиморфизма в Java; наиболее известен из них GJ (Bracha, Odersky,

Stoutamire and Wadler 1998).

Неуточненный термин «полиморфизм» приводит к некоторой путанице при общении различных

программистских сообществ. Среди функциональных программистов (т. е., тех, кто использует или

проектирует языки вроде ML, Haskell и т. п.), он почти всегда означает параметрический полиморфизм.

Среди программистов на объектно-ориентированных языках он, напротив, почти всегда означает по-

лиморфизм через наследование, а параметрический полиморфизм обозначается термином обобщенные

функции.

23.3. Система F

Система, изучаемая нами в этой главе, известна под названием Система F. Ее впервые открыл

Жан-Ив Жирар (Girard 1972), в контексте теории доказательств в логике. Несколько позже систему

rev. 104

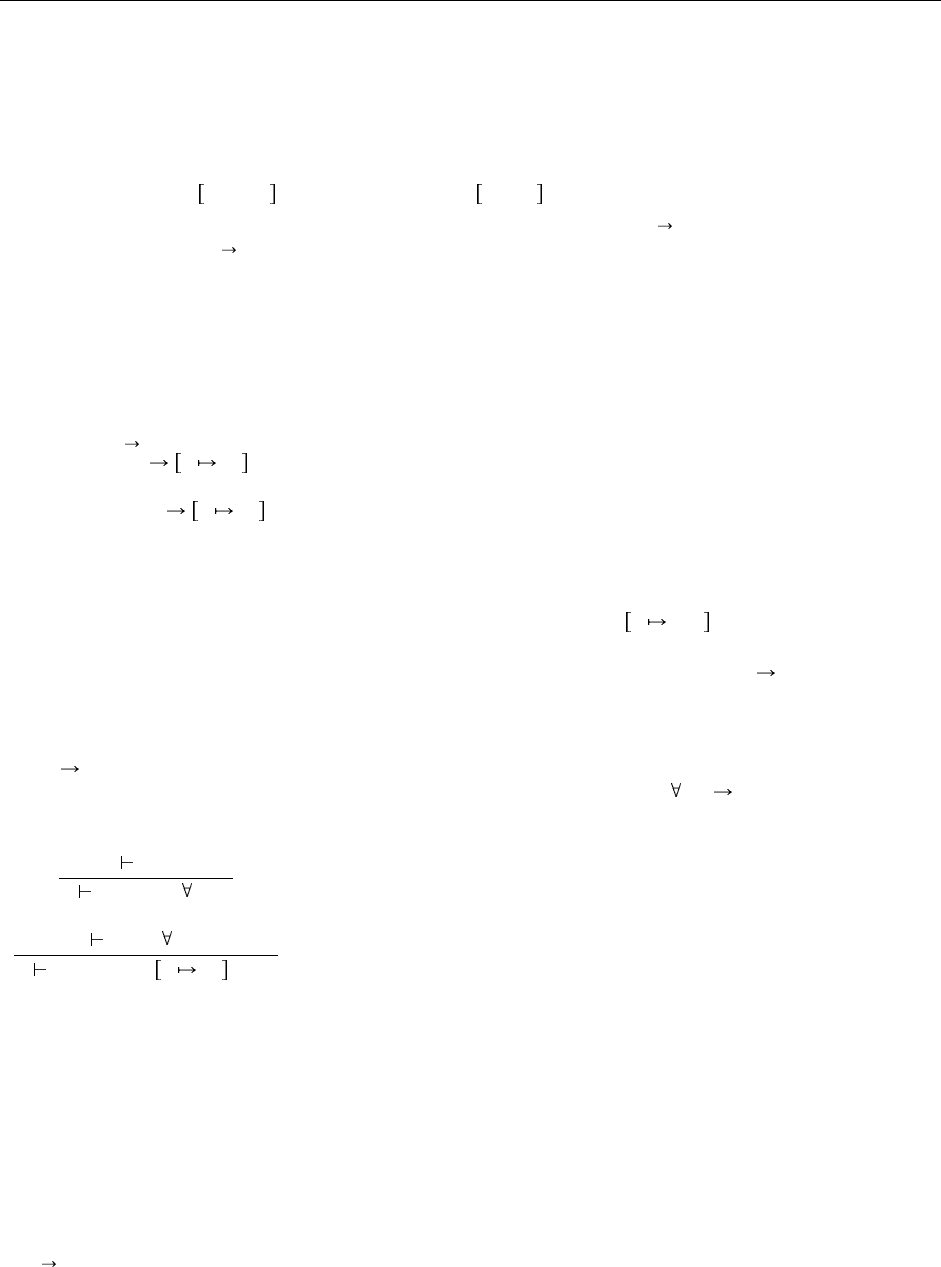
23.3. Система F 267

типов с практически той же выразительной мощностью независимо построил специалист по инфор-

матике Джон Рейнольдс (Reynolds 1975), и назвал ее полиморфное лямбда-исчисление. Эта система

активно используется как исследовательский инструмент для работ по основаниям полиморфизма,

а также послужила базой для многочисленных проектов языков программирования. Иногда ее так-

же называют лямбда-исчислением второго порядка, поскольку по соответствию Карри-Ховарда она

аналогична интуиционистской логике второго порядка, где разрешена квантификация не только по

отдельным объектам термам , но и по предикатам типам .

Определение Системы F является естественным расширением λ , простого типизированного

лямбда-исчисления. В λ лямбда-абстракция служит для абстрагирования термов из термов, а с по-

мощью применения вместо абстрагированных частей подставляются значения. Поскольку теперь нам

понадобился механизм для абстрагирования типов из термов, а также для последующего заполнения

абстракций, мы вводим новую форму абстракции, записываемую λX.t, чьим параметром служит тип,

и новую форму применения, t [T], где аргументом служит выражение типа. Мы называем новые аб-

стракции абстракциями типа, а новую конструкцию применения применением или конкретизацией

типа.

Когда при вычислении абстракция типа сочетается с применением типа, получается редекс, в точ-

ности как в λ . Мы добавляем в систему правило редукции

(λX.t

) [T

] X T

(E-TappTabs)

аналогичное обыкновенному правилу редукции для термов-абстракций и термов-применений

(λx:T

) v

x v

(E-AppAbs)

Например, полиморфная функция тождества

id = λX . λx :X. x;

применяется к типу Nat в выражении id [Nat], а результатом будет X Nat (λx:X.x), т. е., λx:Nat.x,

функция тождества на натуральных числах.

Наконец, мы должны указать тип полиморфной абстракции. Типы вроде Nat Nat используются

для описания обыкновенных функций вроде λx:Nat.x; теперь нам нужен другой вид «функциональ-

ного типа», чьей областью определения служат типы, для описания полиморфных функций вроде id.

Заметим, что для каждого типа-аргумента T, к которому применяется id, она возвращает функцию

вида X X; то есть, тип результата id зависит от конкретного типа, передаваемого ей в качестве ар-

гумента. Чтобы отразить эту зависимость, мы записываем тип id как X.X X. Правила типизации

для полиморфных абстракции и применения аналогичны правилам для абстракции и применения на

уровне термов.

Γ, X t

: T

Γ λX.t

: X.T

(T-TAbs)

Γ t

: X.T

Γ t

] : X T

X.T

(T-TApp)

Обратите внимание, что мы включаем типовую переменную X в контекст, используемый в подвыводе

для t. Продолжает действовать соглашение (5.3.4), что имена переменных (термовых или типовых)

должны быть выбраны так, чтобы отличаться от уже связанных в Γ, и что переменные, связанные

лямбдами, можно при необходимоси переименовывать, чтобы выполнить это условие. (В некоторых

вариантах изложения Системы F это условие новизны задается как явное дополнительное условие в

правиле T-TAbs, а не встраивается в правила построения контекстов, как у нас.) Пока что единствен-

ная роль типовых переменных в контекстах заключается в отслеживании областей видимости и защите

от повторного добавления одной и той же переменной в контекст. В последующих главах мы будем снаб-

жать типовые переменные различной информацией, например, ограничениями (Глава 26) или видами

(Глава 29).

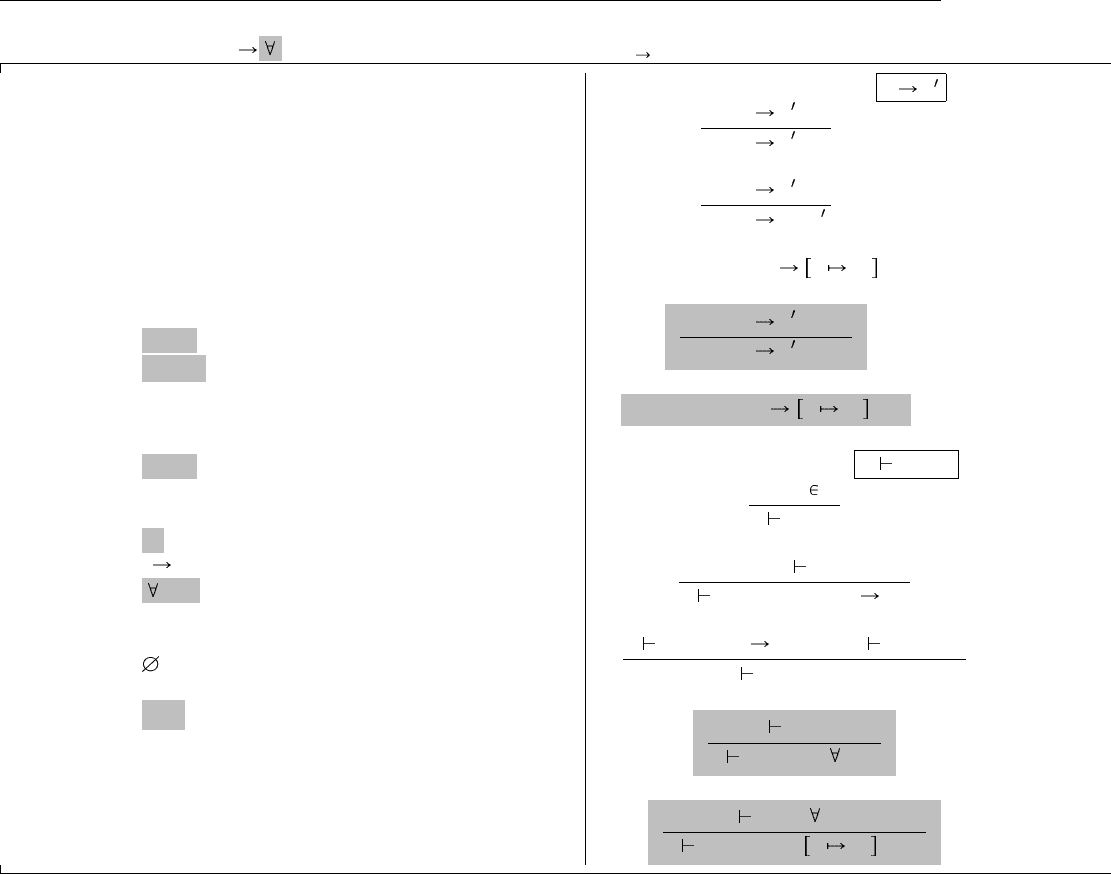
На Рис. 23.1 приведено полное определение полиморфного лямбда-исчисления, и выделены отличия

от λ . Как обычно, здесь определяется только чистое исчисление, без конструкторов типов вроде

записей, без базовых типов вроде Nat и Bool, и без расширений термового языка вроде let и fix. Эти

дополнительные конструкции можно без труда добавить в чистую систему, и в последующих примерах

мы будем их часто использоать.

rev. 104

268 23.4. Примеры

На основе λ (9.1)

Синтаксис

t ::= термы:

x переменная

λx:T.t абстракция

t t применение

λX.t абстракция типа

t [T] применение типа

v ::= значения:

λx:T.t значение-абстракция

λX.t значение-абстракция типа

T ::= типы:

X типовая переменная

T T тип функций

X.T универсальный тип

Γ ::= контексты:

пустой контекст

Γ, x:T связывание термовой переменной

Γ, X связывание типовой переменной

Вычисление t t

(E-App1)

(E-App2)

(λx:T

) v

x v

(E-AppAbs)

] t

]

(E-TApp)

(λX.t

) [T

] X T

(T-TappTabs)

Типизация Γ t : T

x : T Γ

Γ x : T

(T-Var)

Γ, x:T

Γ λx:T

: T

(T-Abs)

Γ t

: T

Γ t

: T

Γ t

: T

(T-App)

Γ, X t

: T

Γ λX.t

: X.T

(T-TAbs)

Γ t

: X.T

Γ t

] : X T

X.T

(T-TApp)

Рис. 23.1. Полиморфное лямбда-исчисление (Система F)

23.4. Примеры

Мы приведем несколько примеров программирования с использованием полиморфизма. Начнем,

для разминки, с нескольких небольших, но усложняющихся примеров, показывающих мощность Си-

стемы F. Затем кратко рассмотрим основные идеи «обыкновенного» полиморфного программирования

со списками, деревьями и т. п. В последних двух разделах вводятся типизированные варианты коди-

рования по Чёрчу для простых алгебраических типов — булевских значений, чисел и списков. (Само

кодирование рассматривалось в Главе 5 для бестипового лямбда-исчисления.) Несмотря на то, что эти

варианты кодирования не имеют особой практической ценности — для этих важных элементов языка

проще породить хороший код, если они встроены как примитивы, — они служат замечательными при-

мерами, на которых можно продемонстрировать как тонкости, так и выразительную силу Системы F. В

Главе 24 мы увидим еще некоторые применения полиморфизма в области модульного программировния

и абстрактных типов данных.

rev. 104

23.4. Примеры 269

23.4.1. Разминка

Мы уже показали, как с помощью абстракции и применения типов определить единую полиморфную

функцию тождества

id = λX . λx . x ;

id : X . X - > X

и как конкретизировать ее, получая любую необходимую в данный момент функцию тождества:

id [ Nat ];

<fun > : Nat -> Nat

id [ Nat ] 0;

0 : Nat

Более полезным примером может служить полиморфная функция удвоения:

do uble = λX. λf:X ->X. λa : X. f ( f a );

do uble : X . (X ->X) -> X -> X

Абстракция по типу X позволяет нам получать функции удвоения для конкретных типов, применяя

double к различным аргументам-типам:

dou b l eNat = double [ Nat ];

dou b l eNat : ( Nat - > Nat ) -> Nat -> Nat

doubleNat A r r o w Na t = doub le [ Nat - > Nat ];

doubleNat A r r o w Na t : (( Nat -> Nat )-> Nat -> Nat ) ->

(Nat - > Nat ) -> Nat -> Nat

Будучи конкретизирована аргументом-типом, double может применяться к конкретной функции и

аргументу, имеющим соответствующие типы:

do uble [ Nat ] (λx : Nat . succ ( succ (x ))) 3;

7 : Nat

Вот чуть более хитрый пример: полиморфное самоприменение. Напомним, что в простом типизиро-

ванном лямбда-исчислении невозможно присвоить тип терму λx. x x (Упражнение 9.3.2). Напротив,

в Системе F этот терм оказывается типизируем, если дать x полиморфный тип и должным образом его

конкретизировать:

se lfApp = λx: X.X -> X . x [ X.X -> X ] x ;

se lfApp : ( X. X - >X ) -> ( X. X -> X)

В качестве (чуть) более полезного примера самоприменения, можно применить к себе самой функцию

double и получить полиморфную функцию учетверения:

qua d r uple = λX . double [X -> X ] ( double [X ]);

qua d r uple : X. (X -> X ) -> X -> X

Упражнение 23.4.1 : При помощи правил с Рис. 23.1 убедитесь, что приведенные выше термы

на самом деле имеют типы, которые им приписываются.

rev. 104

270 23.4. Примеры

23.4.2. Полиморфные списки

Практическое программирование с использованием полиморфизма, как правило, намного прозаич-

нее, чем хитрые примеры из предыдущего подраздела. В качестве примера обыкновенного полиморфно-

го программирования, предположим, что в нашем языке есть конструктор типов List и конструкторы

термов для обычных примитивов работы со списками, чьи типы указаны ниже.

nil : X . List X

cons : X. X -> list X -> List X

isnil : X. List X -> Bool

head : X. List X -> X

tail : X. List X -> List X

Когда мы впервые ввели списки в §11.12, мы позволили применять элементарные операции к спис-

кам с элементами любого типа через правила вывода, сделанные «на заказ», специально для списков.

Теперь мы можем приписать этим операциям полиморфные типы, выражающие в точности те же са-

мые ограничения — то есть, списки больше не надо «вплавлять» в базовый язык; их можно просто

рассматривать как библиотеку, предоставляющую несколько констант, имеющих определенные поли-

морфные типы. То же самое верно для типа Ref и элементарных операций над ссылочными ячейками

из Главы 13, а также для многих других структур данных и управления.

С помощью этих примитивов мы можем определять собственные полиморфные операции над спис-

ками. Например, вот полиморфная функция map, принимающая функцию, переводящую X в Y, и список

X-ов, и возвращающая список Y-ов.

map = λX . λY.

λf : X - >Y.

( fix (λm : ( List X) -> ( List Y ).

λl : List X.

if isnil [X] l

then nil [ Y]

else cons [Y] (f ( head [X ] l ))

(m ( tail [X ] l ))));

map : X . Y . (X ->Y) -> List X -> List Y

l = cons [ Nat ] 4 ( cons [ Nat ] 3 ( cons [ Nat ] 2 ( cons [ Nat ] 1 ( nil [ Nat ]))));

l : list Nat

head [ Nat ] ( map [ Nat ] [ Nat ] (λx : Nat . succ x) l );

5 : Nat

Упражнение 23.4.2 : Убедитесь, что map действительно имеет указанный тип.

Упражнение 23.4.3 Рекомендуется, : Используя в качестве образца map, напишите полиморф-

ную функцию обращения списка

re verse : X . List X -> List X

Это упражнение лучше всего выполнять интерактивно. Запустите интерпретатор fullomega и

скопируйте содержимое файла test.f из каталога fullomega в начало своего файла исходников. (В

этом файле содержатся определения конструктора List и соответствующих операций. Эти опре-

деления требуют мощных возможностей абстракции Системы F

, описываемых в Главе 29. Для

работы с этим упражнением от Вас не требуется полностью понимать, как они работают.)

Упражнение 23.4.4 : Напишите простую полиморфную функцию сортировки

sort : X. (X - >X -> Bool ) -> ( List X ) -> List X

где первым аргументом служит функция сравнения для элементов типа X.

rev. 104