Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

21.9. Подсчет подвыражений 241

Вариант: U, T U, T

и U, T

Поскольку U, T

R, нам известно, что для любого S, S U S T

. По определению , для всех

S должно выполняться также S U S T

. Сдедовательно, U, T U, T

R, согласно

определению R.

Остальные варианты:

Аналогично.

Сочетание двух последних лемм дает нам утверждение, ради которого мы ввели понятие подвыра-

жения при взгляде сверху вниз:

Утверждение 21.9.5 Если S , T reachable

S, T , то либо S S, либо S T, а также либо T S,

либо T T.

Доказательство: Индукция по определению reachable

, с использованием транзитивности .

Конечность reachable

S, T будет следовать (в Утверждении 21.9.11) из последнего доказаного

утверждения в сочетании с тем, что у всякого µ-типа U имеется только конечное число подвыраже-

ний при взгляде сверху вниз. К сожалению, это последнее утверждение неочевидно из определения .

Попытка доказать это путем структурной индукции по U с использованием определения T D терпит

неудачу, поскольку последний вариант в определении T D ломает индукцию: для построения подвыра-

жений U µX.T используется выражение X T T, а оно, возможно, больше по размеру.

В альтернативном понятии подвыражений при взгляде снизу вверх эту проблему удается обойти,

поскольку подстановка µ-типов вместо переменных рекурсии проводится после вычисления подвыра-

жений, а не до. Такое изменение даст нам простое доказательство конечности.

Определение 21.9.6 µ-тип S является подвыражением µ-типа T при взгляде снизу вверх, что запи-

сывается S T, если пара S, T принадлежит наименьшей неподвижной точке следующей порожда-

ющей функции:

BU R T, T T T

S, T

X µX.T S, µX.T S, T R

Это новое определение подвыражений отличается от старого только в варианте для типов, начина-

ющихся с символа µ. Чтобы получить подвыражения такого типа при взгляде сверху вниз, мы сначала

его разворачивали, а затем собирали подвыражения результата развертки. Вычисляя подвыражения

при взгляде снизу вверх, мы сначала собираем (необязательно замкнутые) подвыражения тела, а затем

замыкаем их путем применения развертывающей подстановки.

Упражнение 21.9.7 : Дайте эквивалентное определение отношения в виде набора правил выво-

да.

То, что всякое выражение имеет лишь конечное число подвыражений при взгляде снизу вверх,

доказывается без труда.

Лемма 21.9.8 Множество S S T конечно для любого T.

Доказательство: Прямолинейная структурная индукция по T, с использованием следующих наблю-

дений, которые следуют из определений BU и :

• Если T Top или T X, то S S T T .

• Если T T

либо T T

, то S S T T S S T

S S T

• Если T µX.T , то S S T T X T S S T .

rev. 104

242 21.9. Подсчет подвыражений

Чтобы доказать, что подвыражения типа при взгляде снизу вверх включают его подвыражения

при взгляде сверху вниз, нам потребуется следующая лемма, связывающая подвыражения при взгляде

снизу вверх и подстановку.

Лемма 21.9.9 Если S X Q T, то либо S Q, либо S X Q S для некоторого S T.

Доказательство: Структурная индукция по T.

Вариант: T Top

В определении BU только вариант с рефлексивностью позволяет Top в качестве правого элемента

пары, так что должно быть S Top. Требуемый результат получается при S Top.

Вариант: T Y

Если Y X, имеем S X Q T Q, и требуемый результат следует из условия леммы. Если Y X,

имеем S X Q T Y. Только вариант с рефлексивностью в определении BU может дать нам эту

пару, так что S Y. Требуемый результат получается при S Y.

Вариант: T T

Имеем S X Q T X Q T

. Согласно определению BU , есть три способа, которыми S

может оказаться подвыражением этого типа-произведения при взгляде снизу вверх. Рассмотрим

эти способы по очереди.

Подвариант: S X Q T

Возьмем S T.

Подвариант: S X Q T

Согласно предположению индукции, либо S Q (и тогда мы уже имеем требуемое утверждение),

либо S X Q S для некоторого S T

. В последнем случае получаем требуемый результат

S X Q по определению BU.

Подвариант: S X Q T

Аналогично.

Вариант: T T

Аналогично варианту с типом-произведением.

Вариант: T µY.T

Имеем S X Q T µY. X Q T . Есть два способа, которыми S может отказаться подвыраже-

нием этого типа при взгляде снизу вверх.

Подвариант: S X Q T

Возьмем S T.

Подвариант: S Y µY. X Q T S

, где S

X Q T

Предположение индукции дает нам две возможности:

• S

Q. Согласно нашим соглашениям об именах связанных переменных, изестно, что Y F V Q ,

и отсюда Y F V S

. Но тогда S Y µY. X Q T S

, так что S Q.

• S

X Q S

для некоторого S

T . В таком случае, S Y µY. X Q T S

µY. X Q T X Q S

X Q Y µY.T S

. Требуемый результат получается при S Y

µY.T S

В заключительной части доказательства мы показываем, что всякое подвыражение µ-типа при

взгляде сверху вниз можно найти среди его подвыражений при взгляде снизу вверх.

Утверждение 21.9.10 Если S T, то S T.

Доказательство: Требуется показать, что µTD µBU . По принципу индукции, достаточно по-

казать, что µBU T D-замкнуто — то есть, что T D µBU µBU. Другими словами, нам нужно

показать, что из A, B T D µBU следует A, B µBU BU µBU . Последнее утверждение бу-

дет верно, если для каждого варианта T D, который мог бы породить пару A, B из µBU, найдется

вариант в определении BU, который также порождал бы A, B из µBU . Это тривиально верно для

всех вариантов в определении T D, кроме последнего, поскольку они совпадают с соответствующими

вариантами BU. В последнем варианте A, B S, µX.T T D µBU и S, X µX.T T µBU , или,

что то же самое, S X µX.T T. По Лемме 21.9.9, либо S µX.T, то есть, S, µX.T µBU,

что нам и надо, либо S X µX.T S для некоторого S , такого, что S , T µBU. Из последнего

утверждения следует S, µX.T BU µBU µBU, по последнему варианту в определении BU .

rev. 104

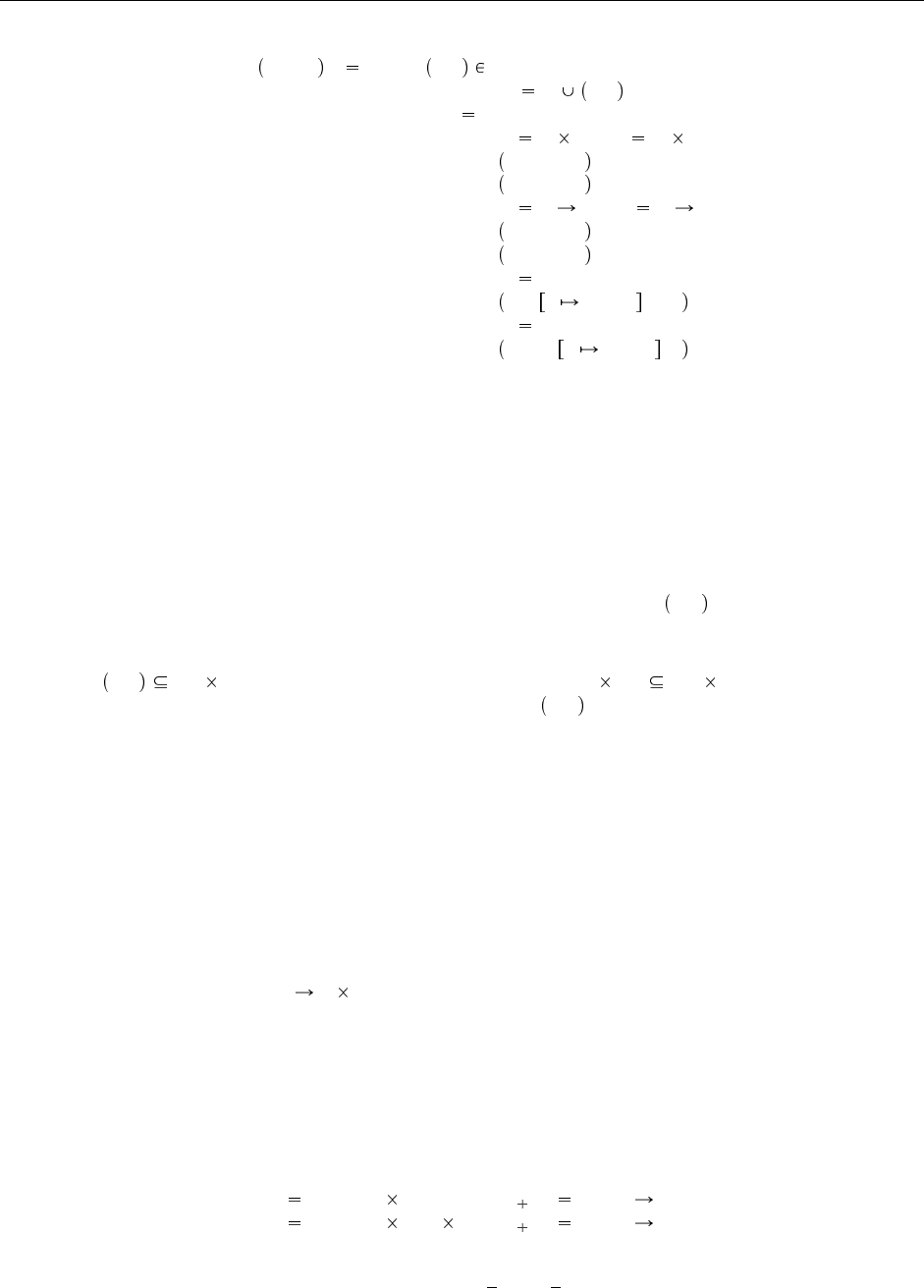
21.10. Отступление: экспоненциальный алгоритм 243

subtype

A, S, T если S, T A, то истина

иначе пусть A

A S, T ,

если T Top, то истина

иначе если S S

и T T

, то

subtype

, S

, T

subtype

, S

, T

иначе если S S

и T T

, то

subtype

, T

, S

subtype

, S

, T

иначе если S µX.S

, то

subtype

, X µX.S

, T

иначе если T µX.T

, то

subtype

, S, X µX.T

иначе ложь

Рис. 21.5. Алгоритм проверки наследования Амадио и Карделли

Сочетая утверждения, доказанные в этом разделе, мы получаем окончательный результат.

Утверждение 21.9.11 Для любых µ-типов S и T, множество reachable

S, T конечно.

Доказательство: Для S и T, пусть T d будет множество их подвыражений при взгляде сверху

вниз, а Bu множество подвыражений при взгляде снизу вверх. Согласно Утверждению 21.9.5,

reachable

S, T T d T d. Согласно Утверждению 21.9.10, T d T d Bu Bu. По Лемме 21.9.8,

последнее множество конечно. Следовательно, reachable

S, T также конечно.

21.10. Отступление: экспоненциальный алгоритм

Алгоритм subtype, представленный в начале §21.9 (Рис. 21.4) можно еще немного упростить, за-

ставив его возвращать булевское значение, а не новое множество гипотез (см. Рис. 21.5). Полученная

при этом процедура, subtype

, соответствует алгоритму Амадио и Карделли для проверки наследо-

вания (Amadio and Cardelli 1993). Она вычислает то же самое отношение, что и subtype, но намного

менее эффективна, поскольку не запоминает пары типов в отношении наследования во время рекур-

сивных вызовов в вариантах для и . Такое, казалось бы, невинное изменение приводит к взрывному

росту количества рекурсивных вызовов, выполняемых алгоритмом. В то время, как количество рекур-

сивных вызовов в алгоритме subtype пропорционально квадрату общего количества подвыражений в

двух типах-аргументах (можно это проверить, исследовав доказательства Леммы 21.9.8 и Утвержде-

ния 21.9.11), в subtype

оно растет экспоненциально.

Экспоненциальное поведение subtype

можно ясно показать на следующем примере. Индуктивно

определим семейства типов S

и T

следующим образом:

µX.Top X S

n 1

µX.X S

µX.Top (Top X) T

n 1

µX.X T

Поскольку S

и T

содержат по одному вхождению S

n 1

и T

n 1

, их размер (после раскрытия сокраще-

ний) линейно зависит от n. Однако проверка S

<: T

порождает вывод, растущий экспоненциально,

rev. 104

244 21.11. Наследование для изорекурсивных типов

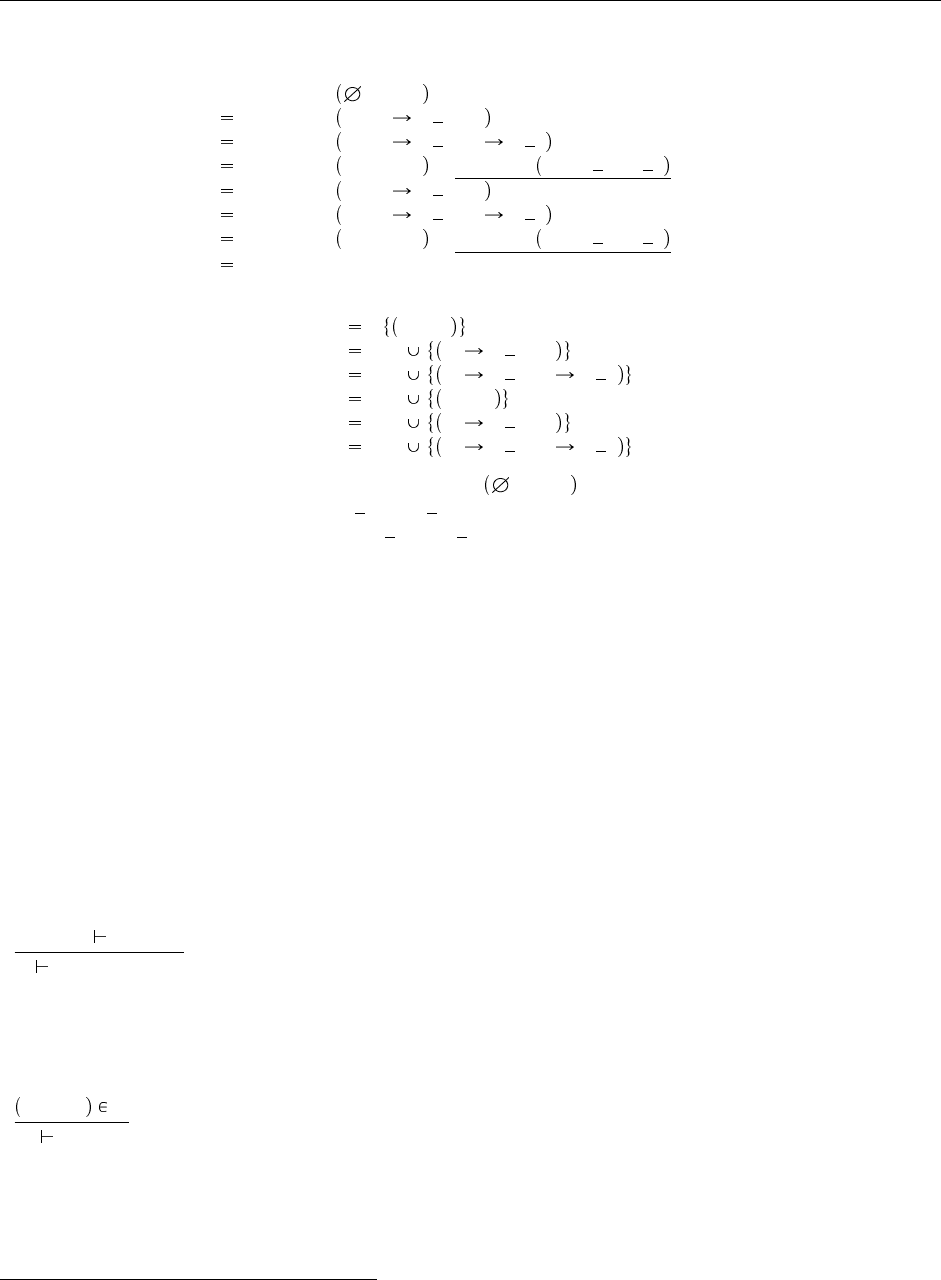
как можно видеть по следующей последовательности рекурсивных вызовов

subtype

, S

, T

subtype

, S

n 1

, T

subtype

, S

n 1

, T

n 1

subtype

, T

, S

и subtype

, S

n 1

, T

n 1

subtype

, T

n 1

, S

и . . .

subtype

, T

n 1

, S

n 1

и . . .

subtype

, S

, T

и subtype

, T

n 1

, S

n 1

и . . .

и т. д.,

где

, T

n 1

, T

n 1

, T

n 1

, S

n 1

, S

n 1

, S

n 1

Обратите внимание, что исходный вызов subtype

, S

, T

приводит к двум рекурсивным вызовам

такого же вида, но с аргументами S

n 1

и T

n 1

. Каждый из них, в свою очередь, приведет к двум

рекурсивным вызовам с аргументами S

n 2

и T

n 2

, и так далее. Таким образом, общее количество

рекурсивных вызовов пропорционально 2

21.11. Наследование для изорекурсивных типов

В §20.2 мы упомянули, что некоторые системы с рекурсивными типами используют изорекурсивное

представление, где свертка и развертка рекурсивных типов явным образом помечается конструкторами

термов fold и unfold. В таких языках конструктор типов µ является «жестким», в том смысле, что

его положение в типе влияет на то, что можно делать с термами данного типа.

Если мы добавим наследование в систему с изорекурсивными типами, жесткость конструктора µ

будет влиять также на отношение наследования. Вместо интуитивного понятия «развернуть до предела,

затем проверить наследование», которое мы применяли на протяжении большей части главы, требуется

напрямую определить правила наследования для рекурсивных типов.

Наиболее распространенное определение изорекурсивного наследования — так называемое Янтар-

ное правило, которое так называется, поскольку стало известным по языку Amber («янтарь») Карделли

(Cardelli 1986):

Σ, X<:Y S <: T

Σ µX.S <: µX.T

(S-Amber)

Интуитивно это правило может читаться так: «Чтобы показать, что µX.S является подтипом µX.T при

некоторых гипотезах Σ, достаточно показать, что S <: T при дополнительном предположении, что X

<: Y».

Σ здесь представляет собой просто множество пар переменных рекурсии, где хранятся уже

рассмотренные пары рекурсивных типов. Эти предположения используются еще в одном правиле на-

следования

X <: Y Σ

Σ X <: Y

(S-Assumption)

позволяющем нам заключить X <: Y, если мы уже это предполагаем.

В сущности. добавление этих двух правил к обычному алгоритму проверки наследования из Гла-

вы 16 (при этом надо еще расширить остальные правила, чтобы они передавали предположения от

предпосылок к заключению) дает нам алгоритм, который ведет себя примерно как алгоритм subtype

с Рис. 21.5, где Σ играет роль A. Разница состоит в том, что (1) «развертка» рекурсивных типов

Заметим, что это правило, в отличие от большинства правил, где на обеих сторонах упоминаются связывающие

конструкции, например, S-All на Рис. 26.1, требует, чтобы перед применением правила связанные переменные X и Y

переименовывались так, чтобы быть различными.

rev. 104

21.12. Дополнительные замечания 245

проводится только тогда, когда они оказываются сразу на обеих сторонах <:, и (2) не проводится под-

становка рекурсивных типов в тела (они просто остаются в виде переменных), и поэтому легко видеть,

что алгоритм всегда завершается.

Правила наследования, встречающиеся в именных системах типов (таких, как Облегченная Java,

Глава 19) близкородственны Янтарному правилу.

Упражнение 21.11.1 Рекомендуется, : Найдите рекурсивные типы S и T, связанные отношени-

ем наследования по эквирекурсивному определению, но не по Янтарному правилу.

21.12. Дополнительные замечания

Эта глава основана на статье-самоучителе Гапеева, Левина и Пирса (Gapeev, Levin and Pierce 2000).

Основные сведения о коиндукции можно найти в «Порочных кругах» (Vicious Circles) Барвайза и

Мосса (Barwise and Moss 1996), самоучителе Гордона по коиндукции и функциональному программиро-

ванию (Gordon 1995), а также во вводной статье Милнера и Тофте по коиндукции в семантике языков

программирования (Milner and Tofte 1991a). Информацию о монотонных функциях и неподвижных

точках см. у Ачеля (Aczel 1977) и у Дэви и Пристли (Davey and Pristley 1990).

Коиндуктивные доказательства стали использоваться в информатике в 1970-е годы, например, в

работах Милнера (Milner 1980) и Парка (Park 1981) по параллелизму; см. также категориальные рас-

суждения Арбиба и Мейнса о дуальности в теории автоматов (Arbib and Manes 1975). Однако индукция

в ее двойственной «ко-» форме была известна математикам намного раньше; она в явном виде исполь-

зовалась, например, в абстрактной алгебре и теории категорий. Основополагающая книга Ачеля (Aczel

1988) о не вполне обоснованных множествах содержит краткий исторический обзор.

Амадио и Карделли (Amadio and Cardelli 1993) построили первый алгоритм проверки наследования

для рекурсивных типов. В их статье определяются три отношения: отношение включения на бесконеч-

ных деревьях, алгоритм, проверяющий наследование для µ-типов, и отношение ссылочного наследова-

ния для µ-типов, определяемое как наименьшая неподвижная точка для набора декларативных пра-

вил вывода; доказывается, что эти три отношения эквивалентны, и все они связываются с модальной

конструкцией, основанной на отношениях частичной эквивалентности. Коиндукция не используется;

вместо этого для рассуждений о бесконечных деревьях вводится понятие конечного приближения к

бесконечному дереву. Это понятие затем играет ключевую роль во многих доказательствах.

Брандт и Хенглейн (Brandt and Henglein 1997) обнажили коиндуктивную суть системы Амадио и

Карделли, дав новую индуктивную аксиоматизацию отношения наследования, корректную и полную

по отношению к аксиомам Амадио и Карделли. Так называемое правило Arrow/Fix в этой аксио-

матизации воплощает коиндуктивность системы. В этой статье описывается общий метод построения

индуктивной аксиоматизации для отношений, которые наиболее естественно описываются через коин-

дукцию, и приводится подробное доказательство завершения для алгоритма проверки наследования.

В §21.9 мы близко следуем ходу этого доказательства. Брандт и Хенглейн показывают, что сложность

их алгоритма O n

Козен, Палсберг и Шварцбах (Kozen, Palsberg and Schwartzbach 1993) получают изящный квадра-

тичный алгоритм из наблюдения, что регулярный рекурсивный тип соответствует автомату с помечен-

ными состояниями. Они определяют понятие произведения для двух автоматов, и получают обыкно-

венный автомат над словами, который принимает слово тогда и только тогда, когда типы, соответству-

ющие исходным автоматам, не находятся в отношении наследования. После этого проверка на пустоту,

проводимая за линейное время, решает задачу проверки наследования. Это, в сочетании с квадратич-

ным временем для построения автомата-произведения и линейным временем преобразования типов в

автоматы, дает общую квадратичную сложность.

Хосойя, Вуайон и Пирс (Hosoya, Vouillon and Pierce 2001) используют родственный подход, основан-

ный на теории автоматов, и устанавливают связь между рекурсивными типами (с объединениями) и

древовидными автоматами, что позволяет построить алгоритм проверки наследования, приспособлен-

ный для задач обработки XML.

Джим и Палсберг (Jim and Palsberg 1999) решают задачу реконструкции типов (см. Главу 22) для

языков с наследованием и рекурсивными типами. Как и мы в этой главе, они используют коиндуктив-

ную точку зрения на отношение наследования для бесконечных деревьев, и обосновывают алгоритм

rev. 104

246 21.12. Дополнительные замечания

проверки наследования как прецедуру, которая строит минимальную симуляцию (т. е., консистентное

множество, в нашей терминологии) для данной пары типов. Они определяют понятия консистентности

и P 1-замыкания для отношения над типами, соответствующие нашим консистентности и множеству

достижимых элементов.

При достаточно долгом

размышлении это утверждение

очевидно.

Сол Горн

rev. 104

Часть V

Полиморфизм

247

Глава 22

Реконструкция типов

Алгоритмы проверки типов для всех виденных нами до сих пор исчислений зависят от явных ан-

нотаций типа — в частности, им нужно, чтобы в лямбда-абстракциях указывался тип аргумента. В

этой главе мы разрабатываем более мощный алгоритм реконструкции типов, способный вычислить

главный тип терма, где аннотации или часть их отсутствуют. Алгоритмы, родственные нашему, лежат

в основе языков вроде ML или Haskell.

Сочетание реконструкции типов с другими языковыми конструкциями часто требует осторожности.

В частности, записи и наследование представляют заметные трудности. Чтобы упростить изложение,

мы в этой книге рассматриваем реконструкцию только для простых типов; в §22.8 можно найти ссылки

на более подробные исследования различных комбинаций.

22.1. Типовые переменные и подстановки

В некоторых исчислениях из предыдущих глав мы предполагали, что множество типов включает в

себя бесконечный набор неинтерпретируемых базовых типов (§11.1). В отличие от интерпретируемых

базовых типов вроде Bool или Nat, к этим типам не прилагается никаких операций создания или

уничтожения термов; интуитивно, они служат просто заглушками для каких-то определенных типов,

настоящая природа которых нас в данный момент не интересует. В этой главе мы будем задавать

вопросы вроде «Если мы заменим заглушку X в терме t конкретным типом Bool, получится ли у нас

типизируемый терм?». Другими словами, мы будем относиться к неинтерпретируемым базовым типам

как к типовым переменным, которые можно конкретизировать с помощью подстановки другими

типами.

С технической точки зрения в этой главе полезно разделить операцию подстановки типов вместо

типовых переменных на две части: нужно описать отображение σ типовых переменных на типы, на-

зываемое подстановка типов, и применить это отображение к конкретному типу T, получая конкре-

тизацию σT. Например, можно определить σ X Bool , а затем применить σ к типу X X, получая

σ X X Bool Bool.

Определение 22.1.1 С формальной точки зрения, подстановка типов (или просто подстановка, ес-

ли из контекста понятно, что речь идет о типах) представляет собой конечное отображение из

типовых переменных в типы. Например, мы записываем в виде X T, Y U подстановку, со-

поставляющую T переменной X и U переменной Y. Запись dom σ обозначает множество типовых

переменных, встречающихся на левой стороне пар, образующих σ, а range σ обозначает множество

типов, встречающихся на правой стороне. Заметим, что одна и та же переменная может при-

надлежать как области определения, так и области значений подстановки. Подобно подстановкам

термов, предполагается, что все компоненты подстановки применяются одновременно; например,

X Bool, Y X X переводит X в Bool, а Y переводит в X X, а не в Bool Bool.

В этой главе рассматривается простое типизированное лямбда-исчисление (Рис. 9.1) с булевскими значениями (8.1),

натуральными числами (8.2) и бесконечным набором базовых типов (11.1). Соответствующие интерпретаторы на OCaml

называются recon и fullrecon.

249

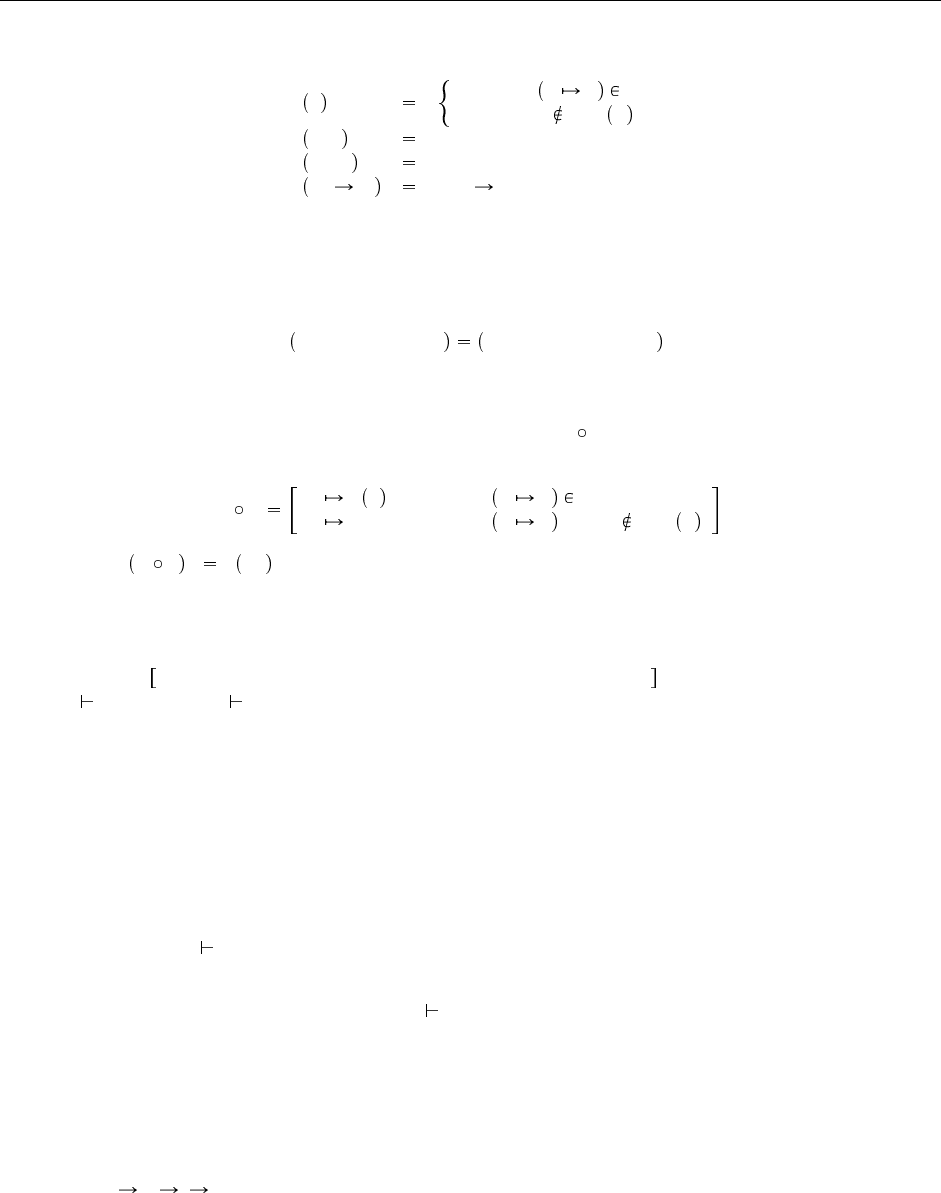
250 22.2. Две точки зрения на типовые переменные

Применение подстановки к типу определяется очевидным образом:

σ X

T если X T σ

X если X dom σ

σ Nat Nat

σ Bool Bool

σ T

σT

Заметим, что нет необходимости предпринимать меры для того, чтобы избежать захвата переменных

при подстановке типов, поскольку в языке выражений типа нет конструкций, связывающих переменные

(такие конструкции появятся в Главе 23).

Подстановка типов поточечно расширяется на контексты при помощи следующего опеределения:

σ x

, . . . , x

:σT

, . . . , x

:σT

Подобным образом, подстановка применяется к терму t путем применения ко всем типам, встречаю-

щимся в его аннотациях.

Если имеются подстановки σ и γ, мы обозначем записью σ γ подстановку, получаемую их компо-

зицией по следующим правилам:

σ γ

X σ T для всех X T γ

X T для всех X T , где X dom γ

Заметим, что σ γ S σ γS .

Ключевое свойство подстановок типов состоит в том, что они сохраняют корректность утверждений

о типизации: если терм, содержащий типовые переменные, правильно тпизирован, таков же будет и

результат применения к нему произвольной подстановки.

Теорема 22.1.2 Сохранение типизации при подстановке типов : Если σ — подстановка ти-

пов, а Γ t : T, то σΓ σt : σT.

Доказательство: Прямолинейная индукция по деревьям вывода типов.

22.2. Две точки зрения на типовые переменные

Предположим, у нас есть терм t, содержащий типовые переменные, и связанный с ним контекст

Γ (возможно, также с типовыми переменными внутри). Можно задать два существенно различных

вопроса, касающихся t:

1. «Все ли конкретизации t правильно типизированы?» А именно, верно ли, что при любой σ мы

будем иметь σΓ σt : T для некоторого T?

2. «Имеются ли правильно типизированные конкретизации t?» А именно, можем ли мы найти

какую-нибудь σ, чтобы выполнялось σΓ σt : T для некоторого T?

Согласно первой точке зрения, типы переменных должны оставаться абстрактными во время про-

верки типов; таким образом, мы можем быть уверены, что правильно типизированный терм будет

правильно себя вести, какие бы типы мы ни подставили вместо его типовых переменных. Например,

терм

λf :X ->X. λa : X. f ( f a );

имеет тип (X X) X X и, каким бы конкретным типом T бы мы ни заменили X, конкретизация

λf :T ->T. λa : T. f ( f a );

окажется правильно типизирована. Отношение к типовым переменным как к абстракциям типа ведет

к параметрическому полиморфизму. Типовые переменные кодируют утверждение, что терм можно

использовать в различных контекстах с различными конкретными типами. Мы вернемся к параметри-

ческому полиморфизму позднее в этой главе (§22.7), а также, более подробно, в Главе 23.

rev. 104