Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

Часть IV

Рекурсивные типы

211

Глава 20

Рекурсивные типы

В разделе 11.12 мы увидели, как расширить простую систему типов, чтобы она включала кон-

структор типов List(T), описывающих списки с элементами типа T. Списки — лишь один из примеров

большого класса распространенных структур, — в него входят также очереди, бинарные деревья, поме-

ченные деревья, деревья абстрактного синтаксиса и т.п., — которые могут вырастать до произвольного

размера, но при этом имеют простую, регулярную структуру. Например, элемент List(Nat) всегда яв-

ляется либо nil, либо парой («ячейкой cons»), состоящей из числа и List(Nat). Очевидно, что не имеет

смысла представлять каждую из этих структур как отдельную элементарную языковую конструкцию.

Вместо этого нам нужен общий механизм, с помощью которого они в случае необходимости могут быть

определены на основе более простых элементов. Этот механизм называется рекурсивными типами.

Давайте снова рассмотрим тип списков чисел

. Мы можем представить утверждение, что список

является либо nil, либо парой, при помощи вариантных типов и типов кортежей, определенных в

разделах 11.10 и 11.7:

Na tList = < nil : Unit , cons :{... ,...} >;

Значение, связанное с меткой варианта nil, тривиально, поскольку уже сама метка nil сообщает нам

все, что требуется знать о пустом списке. В то же время значение, связанное с cons, является парой,

состоящей из числа и другого списка. Первый компонент этой пары имеет тип Nat,

Na tList = < nil : Unit , cons : { Nat , ...} >;

а второй компонент является списком чисел, т.е. элементом того самого типа NatList, который мы в

данный момент определяем:

Na tList = < nil : Unit , cons :{ Nat , NatList } >;

Это уравнение не является обыкновенным определением, — а именно, мы не даем здесь новое имя

выражению, чье значение нам заранее понятно, — поскольку в правой части используется то самое

имя, которое подлежит определению. Напротив, это уравнение можно рассматривать как определение

В этой главе рассматривается простое типизированное исчисление с рекурсивными типами. В примерах используются

различные конструкции из предыдущих глав; соответствующий интерпретатор называется fullequirec. Для раздела 20.2

интерпретатором служит fullisorec.

До конца этой главы мы не будем касаться вопроса, как дать единое обобщенное определение списков с элементами

произвольного типа T. Для этого определения нам понадобится механизм операторов над типами, который будет введен

в главе 29.

213

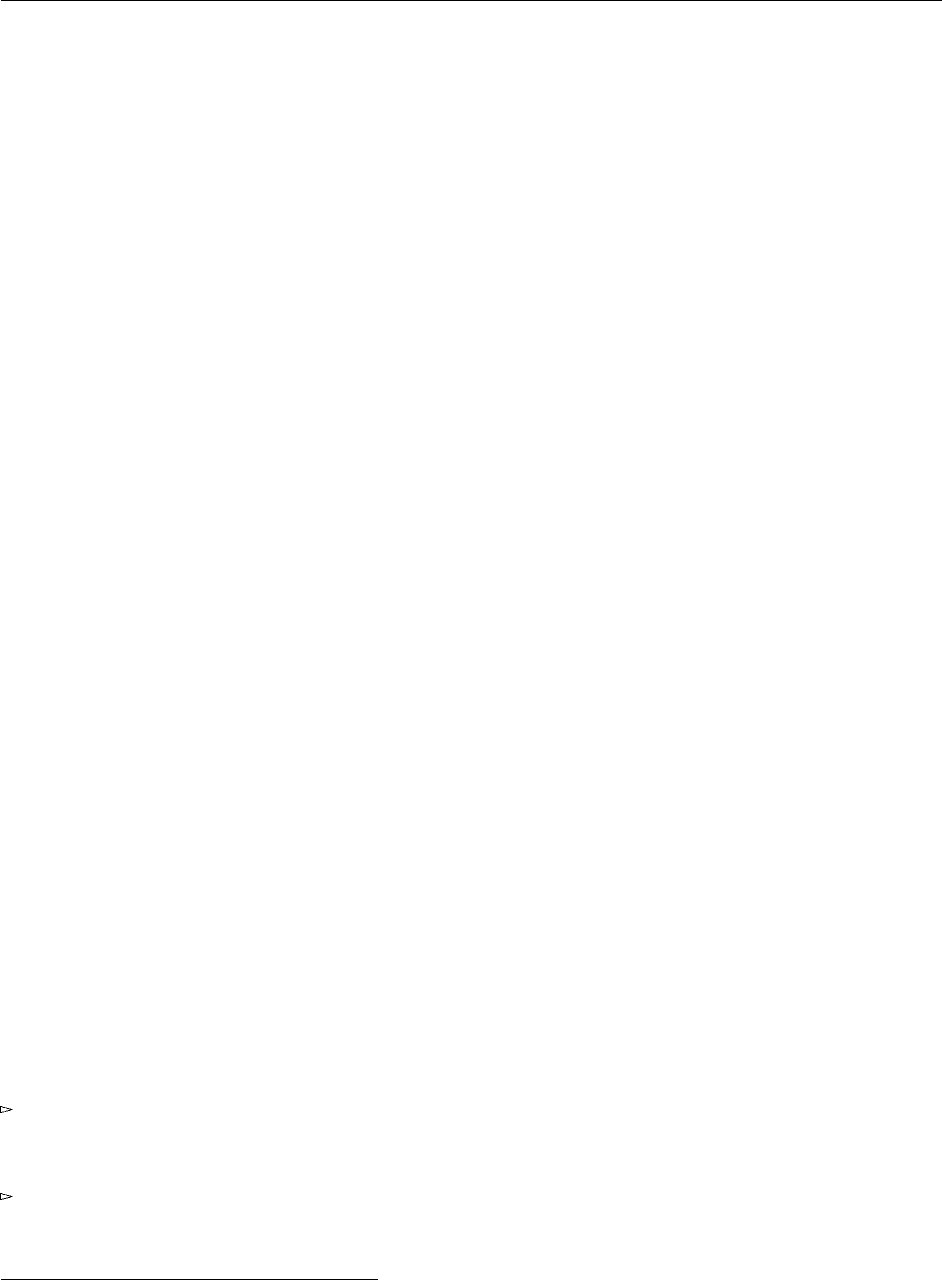
214 20.1. Примеры

бесконечного дерева:

<nil:



,cons:

Unit

{



}

Nat

<nil:



,cons:

Unit

{



}

Nat

<nil:



,cons:

Unit

Рекурсивное уравнение, определяющее это бесконечное дерево, подобно уравнению, через которое опре-

деляется рекурсивная функция факториала, приведенному на стр. 50. Так же как и там, нам будет

удобно преобразовать это уравнение в правильное определение, переместив «цикл» в правую часть

выражения.

Мы сделаем это путем введения явного оператора рекурсии µ для типов:

Na tList = µX. < nil : Unit , cons :{ Nat ,X }>;

Интуитивно это выражение читается так: «Пусть NatList будет бесконечным типом, удовлетворяющим

уравнению X = <nil:Unit, cons:{Nat,X}>».

В разделе 20.2 мы увидим, что существуют два немного различных способа формализации рекур-

сивных типов – так называемые эквирекурсивное и изорекурсивное представления. Они отличаются в

том, сколько помощи для системы проверки типов ожидается от программиста в виде аннотаций. В

примерах, приведенных в следующем разделе, мы будем использовать более простое эквирекурсивное

представление.

20.1. Примеры

20.1.1. Списки

Для начала давайте закончим пример со списками чисел, начатый нами в предыдущем разделе.

Чтобы программировать с использованием этих списков, нам нужна константа nil, конструктор cons

для добавления элементов в начало существующего списка, операция isnil, которая принимает в ка-

честве аргумента список и возвращает булево значение, а также операции декомпозиции hd и tl для

извлечения первого элемента и остатка из непустого списка. На Рис. 11.13 мы определяли их все как

встроенные операторы; теперь нашей задачей будет построить их из базовых элементов.

Определение nil и cons немедленно следуют из определения NatList как двухэлементного вариант-

ного типа.

nil = <nil =unit > as NatL ist ;

nil : NatL ist

cons = λn : Nat . λl: NatList . <cons ={ n, l }> as N atList ;

cons : Nat -> Nat List -> Na tList

(Напомним из §11.12, что выражение вида <l=t> as T используется для создания значений вариант-

ного типа: значение t помечается меткой l и «вставляется» в вариантный тип T. Заметим также, что

Такое перемещение оказывается удобно потому, что оно позволит нам говорить о рекурсивных типах без их явного

именования. Однако работа с явно именованными рекурсивными типами также имеет свои преимущества — см. обсуж-

дение именных и структурных систем типов в §19.3.

rev. 104

20.1. Примеры 215

процедура проверки типов автоматически «развернет» рекурсивный тип NatList в вариантный тип

<nil:Unit, cons:{Nat,NatList}>.)

Остальные базовые операции над списками проверяют их структуру и извлекают отдельные их

части. Они реализуются в терминах case.

isnil = λl : Na tList . case l of

<nil =u > => true

| < cons =p > = > false ;

isnil : NatL ist -> Bool

hd = λl : NatLis t . case l of <nil =u > => 0 | < cons =p > = > p .1;

hd : NatList -> Nat

tl = λl : NatLis t . case l of <nil =u > => l | < cons =p > = > p .2;

tl : NatList -> NatL ist

Мы приняли волевое решение, что выполнение hd для пустого списка будет возвращать 0, а выпол-

нение tl для пустого списка будет возвращать пустой список. В этих случаях можно было бы также

возбуждать исключения.

С помощью всех этих определений можно написать рекурсивную функцию, которая суммирует

элементы списка:

su mlist = fix (λs: NatLi st -> Nat . λl: NatL ist .

if isnil l then 0 else plus ( hd l ) ( s ( tl l )));

su mlist : NatLis t -> Nat

my list = cons 2 ( cons 3 ( cons 5 nil ));

su mlist my list ;

10 : Nat

Заметим, что хотя сам NatList — бесконечное типовое выражение, все его элементы являются конечны-

ми списками. Причина в том, что ни примитивы построения пары и пометки вариантов, ни конструкция

fix с вызовом по значению не пригодны для построения бесконечно больших структур.

Упражнение 20.1.1 : Один из способов представления помеченных двоичных деревьев говорит,

что дерево может быть либо листом (без метки), либо внутренним узлом с численной меткой и

двумя дочерними деревьями. Определите тип NatTree и соответствующий набор операций для со-

здания, выделения элементов и проверки структуры дерева. Напишите функцию, которая будет вы-

полнять обход дерева «в глубину» и возвращать список найденных меток. Для тестирования вашего

кода используйте интерпретатор fullequirec.

«Жадные» функции

Другим примером, демонстрирующим немного более хитрое использование рекурсивных типов, яв-

ляется тип «жадных функций», которые могут принимать любое количество численных аргументов, и

всегда возвращают новую функцию, столь же «жадную»:

Hu ngry = µA. Nat -> A;

Элементы этого типа могут быть определены с использованием оператора fix:

f = fix (λf: Nat -> Hu ngry . λn: Nat . f );

f : H ungry

f 0 1 2 3 4 5;

<fun > : Hungry

rev. 104

216 20.1. Примеры

20.1.2. Потоки

Более полезным вариантом типа Hungry, показанного выше, является тип Stream (поток), состоящий

из функций, которые могут потреблять любое количество значений unit, каждый раз возвращая пару,

состоящую из числа и нового потока.

St ream = µA. Unit -> { Nat , A};

Мы можем определить две операции декомпозиции для потоков; если s — поток, то результатом hd s

будет первое число, которое он вернет когда мы передадим ему unit.

hd = λ: Strea m . ( s unit ).1;

hd : Stream -> Nat

Подобным образом, результатом tl s будет новый поток, который мы получим, если передадим unit в

tl = λs : Stream . ( s unit ).2;

tl : Stream -> Stream

Для создания потока мы снова используем оператор fix:

up from0 = fix (λf: Nat -> St ream . λn: Nat . λ_: Unit . {n ,f ( succ n )}) 0;

up from0 : S tream

hd upfrom0 ;

0 : Nat

hd ( tl ( tl ( tl upfro m0 )));

3 : Nat

Упражнение 20.1.2 Рекомендуется, : Определите поток, выдающий элементы последователь-

ности чисел Фибоначи (1, 1, 2, 3, 5, 8, 13, ...).

Потоки можно дальше обобщить до простой формы процессов – функций, принимающих число, а

возвращающих число и новый процесс.

Pr ocess = µA. Nat -> {Nat , A};

Например, вот процесс, который на каждом шаге возвращает сумму всех элементов, полученных им

до сих пор:

p = fix (λf: Nat -> Pro cess . λacc : Nat . λn : Nat .

let newacc = plus acc n in

{ newacc , f newacc }) 0;

p : Proces s

Как мы это делали и для потоков, можно определить вспомогательные функции для взаимодействия

с процессами:

curr = λs : P rocess . (s 0).1;

curr : Pro cess -> Nat

send = λn : Nat . λs: Process . ( s n ).2;

send : Nat -> Pro cess -> Pr ocess

Если мы передадим процессу p числа 5, 3 и 20, то число, которое он вернет в ответ на последнее

обращение, будет 28.

curr ( send 20 ( send 3 ( send 5 p )));

28 : Nat

rev. 104

20.1. Примеры 217

20.1.3. Объекты

Небольшое переосмысление последнего примера дает нам еще одну известную идиому взаимодей-

ствия с данными – объекты. Например, вот тип для объектов-счетчиков (counter), которые хранят

внутри себя число и позволяют либо выполнять запросы для получения этого числа, либо увеличивать

его:

Co unter = µC. { get : Nat , inc : Unit -> C };

Заметим, что наше взаимодействие с объектами является чисто функциональным (так же как и в

Главе 19, и в отличие от того, которое было в Главе 18): отправка сообщения inc объекту-счетчику не

вызывает изменение внутреннего состояния объекта; вместо этого операция возвращает новый объект-

счетчик, в котором как раз и изменено внутреннее состояние. В этом случае использование рекурсивных

типов позволило нам указать, что возвращаемый объект имеет тот же самый тип, что и оригинал.

Единственное отличие между этими объектами и процессами, которые мы обсуждали выше, состоит

в том, что объект является рекурсивно определенной записью (содержащей функцию), в то время как

процесс — рекурсивно определенная функция (возвращающая кортеж). Польза от такой смены точки

зрения в том, что мы можем расширить нашу запись и включить в нее более одной функции, например,

добавив операцию уменьшения значения:

Co unter = µC. { get : Nat , inc : Unit -> C , dec : Unit -> C };

Для создания объекта counter мы используем комбинатор неподвижной точки, как мы это делали выше.

c = let create = fix (λf : { x: Nat } -> Counter . λs: {x : Nat }.

{ get = s.x ,

inc = λ_ : Unit . f {x= succ (s . x )} ,

dec = λ_ : Unit . f {x= pred (s . x )} })

in crea te {x =0};

c : Counte r

При вызове операций над c мы просто выделяем соответствующее поле:

c1 = c . inc unit ;

c2 = c1 . inc unit ;

c2 . get ;

2 : Nat

Упражнение 20.1.3 : Расширьте тип Counter и счетчик c, приведенный выше, чтобы они вклю-

чали операции backup и reset (как мы это делали в §18.7): выполнение backup заставляет счетчик

сохранить его текущее значение в специальном внутреннем регистре, а вызов reset приводит к вос-

становлению значения из этого регистра.

20.1.4. Рекурсивные значения на основе рекурсивных типов

Более удивительное использование рекурсивных типов, ясно показывающее их выразительную си-

лу — построение правильно типизированного комбинатора неподвижной точки. Для любого типа T мы

следуюшим образом можем определить конструктор неподвижной точки для функции над T.

fix

= λf: T -> T. (λx :(µA. A -> T ). f (x x )) (λx :(µA.A -> T ). f (x x ));

fix

: (T -> T ) -> T

Заметим, что если мы сотрем типы, этот терм будет выглядеть в точности как бестиповый комбинатор

неподвижной точки, рассмотренный нами на стр. 59.

Здесь основной трюк заключается в использовании рекурсивного типа для двух вхождений выра-

жения x x. Как мы видели в Упражнении 9.3.2, типизация этого терма требует, чтобы x имел функци-

ональный тип, чьей областью значений является сам x. Ясно, что конечного типа с таким свойством

не существует, но бесконечный тип µA.A -> T прекрасно справляется с задачей.

rev. 104

218 20.1. Примеры

Из этого примера следует, что присутствие рекурсивных типов ломает свойство строгой нормализа-

ции: с помощью комбинатора fix

можно написать правильно типизированный терм, чье вычисление

(при применении к unit) никогда не завершится.

di verge

= λ_: Unit . fix

(λx : T . x );

di verge

: Unit -> T

Более того, поскольку такие термы можно построить для любого типа, отсюда следует, что каждый

тип в этой системе является населенным (т. е., имеет элементы), в отличие от λ .

20.1.5. Интерпретация бестипового лямбда-исчисления

Возможно, лучшая иллюстрация мощи рекурсивных типов — то, что бестиповое лямбда-исчисление

можно полностью включить, — правильно типизированным образом, — в статически типизированный

язык с рекурсивными типами. Допустим, что D имеет следующий тип:

D = µX.X -> X;

Определим «функцию включения» lam, отображающую функции из D в D в элементы D, как показано

ниже:

lam = λf : D -> D . f as D ;

lam : D

Для применения одного элемента D к другому мы просто раскрываем тип первого, выделяем функцию

и применяем ее ко второму:

ap = λf :D . λa:D . f a;

ap : D

Предположим теперь, что M – закрытый лямбда-терм, содержащий только переменные, абстракции и

применения. В таком случае, мы можем сконструировать элемент D, представляющий M и записываемый

как M , с помощью общего метода, представленного ниже:

x x

λx.M lam (λx:D. M )

M N ap M N

Например, вот бестиповой комбинатор неподвижной точки, выраженный как элемент D:

fixD = lam (λf : D .

ap ( lam (λx: D . ap f ( ap x x )))

( lam (λx : D . ap f ( ap x x ))));

fixD : D

Это внедрение чистого лямбда-исчисления можно расширить и включить в него другие элементы,

например, числа. Заменяем определение D на вариантный тип с одним вариантом для чисел и одним

для функций:

D = µX. < nat : Nat , fn :X -> X >;

Таким образом элемент D является либо числом, либо функцией из D в D, соответственно помеченной

nat или fn. Реализация конструктора lam практически такая же, как и выше:

Этот факт делает системы с рекурсивными типами бесполезными в качестве логик: если мы рассматриваем типы как

логические утверждения согласно соответствию Карри-Ховарда (см. §9.4), и читаем «тип T населен» как «утверждение

T является доказуемым», то то, что каждый тип населен, означает, что каждое утверждение в логике доказуемо — то

есть, что логика является противоречивой.

Читатели, знакомые с денотационной семантикой, заметят, что определиние D в точности совпадает с определяющим

свойством универсальных доменов, используемых в семантических моделях чистого лямбда-исчисления.

rev. 104

20.2. Формальные определения 219

lam = λf : D -> D . <fn =f > as D;

lam : ( D -> D) -> D

Однако реализация ap интересным образом отличается:

ap = λf :D . λa:D .

case f of

<nat =n > => dive r geD unit

| < fn =f > = > f a ;

ap : D -> D -> D

Прежде, чем нам удастся применить f к a, нужно выделить функцию f с помощью case. При этом

требуется указать, как наше применение ведет себя, если f не является функцией. (В этом примере мы

просто зацикливаемся; можно было бы также возбудить исключение). Заметьте, как сильно проверка

метки в этом примере похожа на проверку метки во время выполнения в динамически типизирован-

ных языках вроде Scheme. В этом смысле можно сказать, что типовое вычисление «включает в себя»

бестиповое или динамически типизированное вычисление.

Аналогичная проверка меток необходима при определении функции следования для элементов D:

suc = λf : D. case f of

<nat =n > => (< nat = succ n > as D)

| < fn =f > = > divergeD unit ;

suc : D -> D

Включение 0 в D тривиально:

zro = <nat =0 > as D ;

zro : D

Упражнение 20.1.4 : Дополните это кодирование булевыми значениями и условными выражения-

ми, и закодируйте термы, if false then 1 else 0 и if false then 1 else false в качестве эле-

ментов D. Что происходит при вычислении этих термов?

Упражнение 20.1.5 Рекомендуется, : Расширьте тип данных D, чтобы он включал записи,

D = µX. < nat : Nat , fn :X -> X , rcd : Nat -> X >;

и реализуйте создание записей и проекцию полей. Для простоты в качестве меток полей используйте

натуральные числа, — т.е. записи представляются как функции из натуральных чисел в элементы

D. Проверьте свое расширение интерпретатором fullequirec.

20.2. Формальные определения

В литературе о системах типов существует два основных подхода к рекурсивным типам. Основное

отличие между ними заключается в ответе на простой вопрос: каково отношение между типом µX.T и

его одношаговой разверткой? Например, как соотносятся NatList и <nil:Unit,cons:{Nat,NatList}>?

1. При эквирекурсивном подходе эти два типовых выражения рассматриваются как эквивалентные

по определению — взаимозаменяемые во всех контекстах, — поскольку они обозначают одно и

то же бесконечное дерево.

Процедура проверки типов отвечает за то, чтобы термы одного типа

были допустимы в качестве аргументов функции, ожидающей термы другого, и т. п.

Приятной особенностью эквирекурсивного подхода является то, что единственное изменение по

сравнению с декларативными представлениями уже известных нам систем — то, что требует-

ся допустить, что типовые выражения могут быть бесконечными.

Существующие определения,

Отображение из µ-типов в бесконечные деревья формально определено в §21.8.

Строго говоря, мы должны сказать регулярными — см. §21.7.

rev. 104

220 20.2. Формальные определения

теоремы о типовой безопасности и доказательства остаются неизмененными, поскольку они не

зависят от индукции по типовым выражениям (которая, естественно, больше не работает).

Конечно, реализация эквирекурсивных типов требует некоторой работы, поскольку алгоритмы

проверки типов не могут напрямую работать с бесконечными структурами. Детали того, как это

может быть осуществлено, приводятся в главе 21.

2. С другой стороны, при изорекурсивном подходе рекурсивный тип и результат шага его развертки

считаются различными, но изоморфными типами.

С формальной точки зрения, раскрытием рекурсивного типа µX.T является тип, полученный пу-

тем взятия тела T и замены всех вхождений X на весь рекурсивный тип, т. е., используя стандарт-

ную нотацию для подстановки, X µX.T T. Например, тип NatList, т. е.

µX .< nil : Unit , cons :{ Nat ,X} > ,

раскрывается в

<nil : Unit , cons :{ Nat , µX .< nil : Unit , cons :{ Nat ,X } >} >.

В системе с изорекурсивными типами для каждого рекурсивного типа µX.T мы вводим пару

функций

unfold[µX.T] : µX.T X µX.T T

fold[µX.T] : X µX.T T µX.T

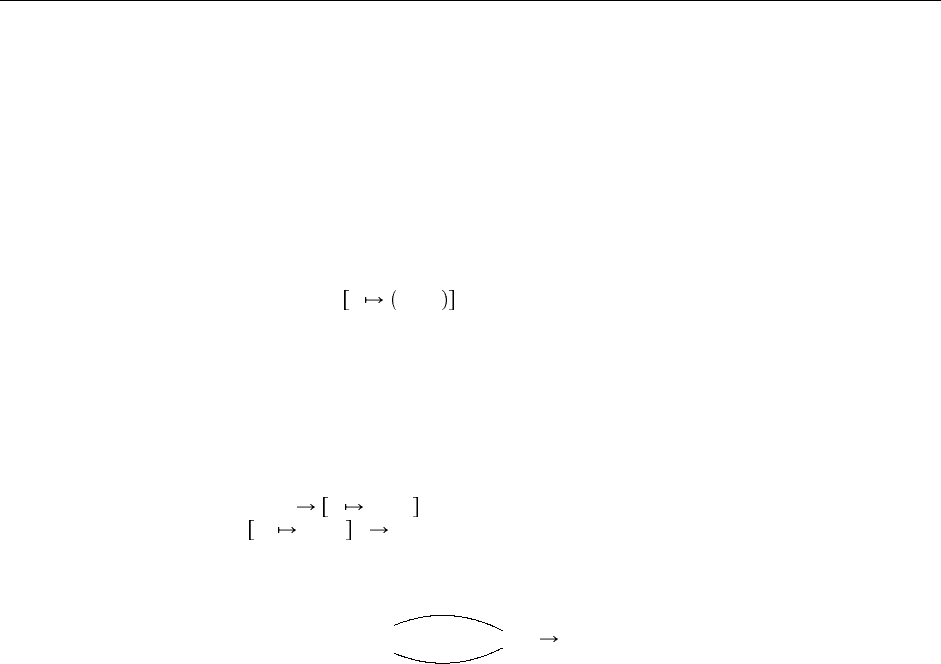
которые «свидетельствуют об изоморфизме» через отображение (в обе стороны) значений между

двумя типами:

µX.T

unfold[µcodeX.T]

[X µX.T] T

fold[µX.T]

Отображения fold и unfold реализованы в качестве примитивов языка, как это показано на

Рис. 20.2. То, что они образуют изоморфизм, отражается в правиле вычисления E-UnfldFld,

уничтожающем выражение fold, когда оно оказывается в паре с соответствующим unfold. (Пра-

вило вычисления не требует, чтобы аннотации типов для fold и unfold были одинаковыми, по-

скольку для проверки такого ограничения нам пришлось бы запускать процедуру проверки типов

во время выполнения. Однако в правильно типизированной программе эти две аннотации типов

будут равны при всяком применении E-UnfldFld.)

Оба подхода широко используются как в теоретических исследованиях, так и при проектировании

языков программирования. Эквирекурсивный стиль, пожалуй, легче понять интуитивно, но он более

требователен к процедуре проверки типов, поскольку она должна эффективно находить точки, где

следует добавить аннотации fold и unfold. Более того, взаимодействие между эквирекурсивными ти-

пами и другими нетривиальными типовыми возможностями, такими, как ограниченная квантифиации

и операторы над типами, бывает достаточно сложным и приводит к значительным теоретическим труд-

ностям (см., например, Ghelli, 1993; Colazzo and Ghelli, 1999) или даже к тому, что задача проверки

типов оказывается неразрешимой (Solomon, 1978).

Изорекурсивный стиль несколько тяжеловеснее по части обозначений — он требует, чтобы про-

граммы были оформлены с помощью инструкций fold и unfold в каждой точке, где употребляются

рекурсивные типы. Однако на практике эти аннотации часто можно «спрятать», слив их с аннотациями

другого рода. Например, в языках семейства ML каждое определение datatype неявно вводит рекур-

сивный тип. Каждое использование одного из конструкторов при построении значения конкретного

типа данных неявно включает fold, а конструктор, встречающийся в сопоставлении с образцом, неяв-

но применяет unfold. Подобным образом, в Java каждое определение класса вводит рекурсивный тип,

и выполнение метода объекта включает неявный unfold. Это удачное перекрытие механизмов делает

изорекурсивный стиль достаточно удобным для практического использования.

Например, вот пример NatList в изорекурсивном виде. Удобно будет сначала определить сокраще-

ние для развернутой формы NatList:

rev. 104