Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

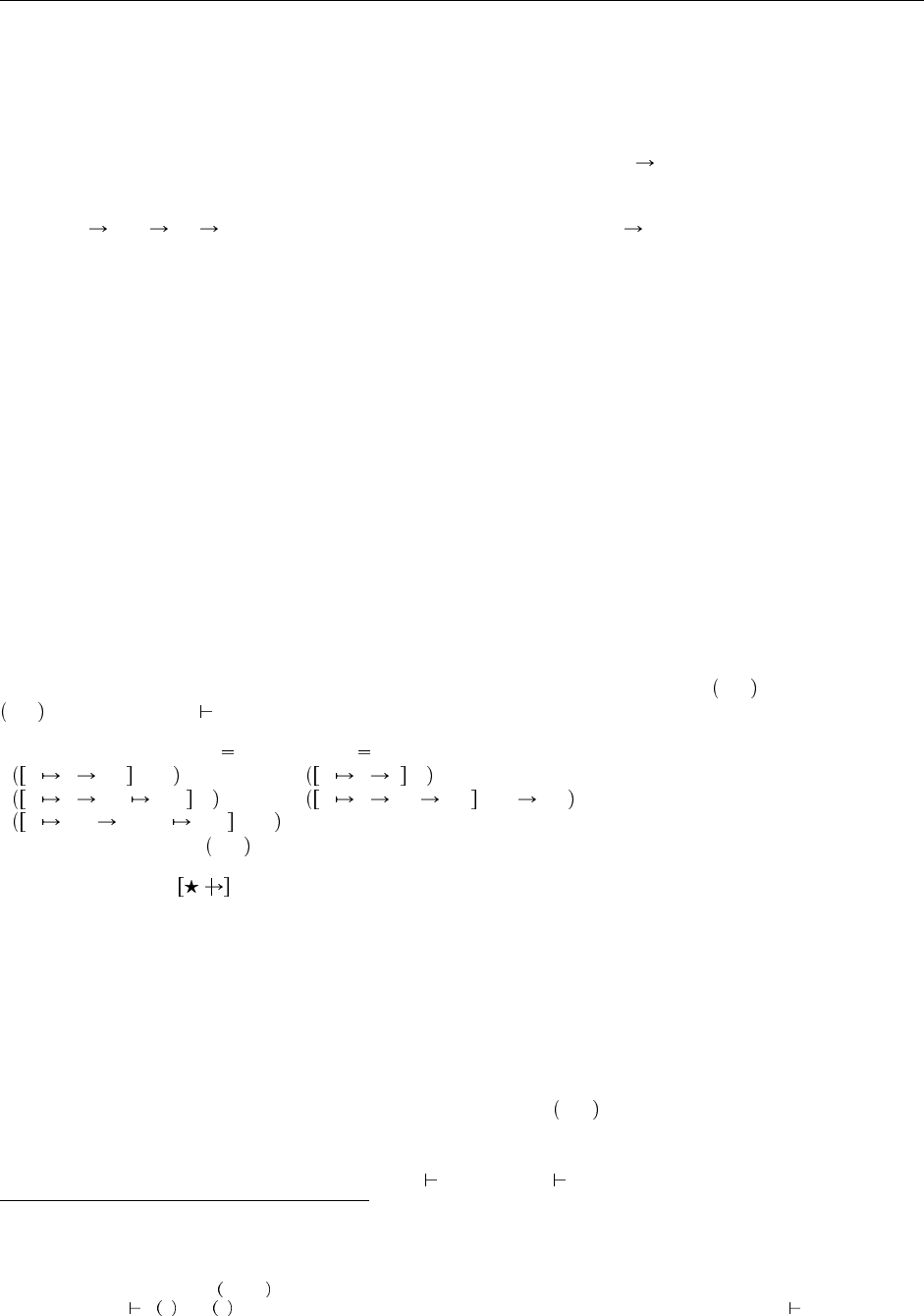
22.3. Типизация на основе ограничений 251

При второй точке зрения терм t даже не обязан быть правильно типизирован; мы хотим узнать, воз-

можно ли конкретизировать его до правильно типизированного терма, выбрав подходящие значения

некоторым из его типовых переменных. Например, терм

λf :Y. λa: X . f ( f a );

в приведенном виде не типизируем, однако, если мы заменим Y на Nat Nat, а X на Nat, мы получим

λf :Nat - > Nat . λa: Nat . f ( f a );

типа (Nat Nat) Nat Nat. Или же, если мы просто заменим Y на X X, получим терм

λf :X ->X. λa : X. f ( f a );

правильно типизированный, несмотря на наличие переменных. На самом деле, этот терм — наиболее

общая конкретизация λf:Y. λa:X. f (f a), в смысле, что такая подстановка принимает наименьшие

обязательства, касающиеся значений типовых переменных, среди подстановок, дающих в результате

правильно типизированный терм.

Поиск корректных конкретизаций для типовых переменных является основой идеи реконструкции

типов (иногда ее называют вывод типов), когда компилятор помогает восстановить информацию о

типах, опущенную программистом. В предельном случае можно, как в ML, позволить программисту

опускать все аннотации типа и писать на языке чистого, бестипового лямбда-исчисления. Во время

синтаксического анализа мы снабжаем каждую «голую» лямбда-абстракцию λx.t переменной типа

λx:X.t, выбирая при этом X отличным от типовых переменных всех других абстракций в программе.

Затем мы проводим реконструкцию типов и находим самые общие значения для всех этих переменных,

позволяющие терму пройти проверку типов. (Схема несколько усложняется, если в языке, как в ML,

присутствует полиморфизм через let; мы вернемся к этому вопросу в §22.6 и §22.7.)

Чтобы формализовать реконструкцию типов, нам потребуется способ кратко обозначать возможные

способы подстановки типов вместо типовых переменных в терме и связанном с ним контексте, при

которых получается правильное утверждение о типизации.

Определение 22.2.1 Пусть имеется контекст Γ и терм t. Решением для Γ, t называется пара

σ, T , такая, что σΓ σt : T.

Пример 22.2.2 Пусть Γ f:X, a:Y, а t f a. Тогда

X Y Nat , Nat X Y Z , Z

X T Z, Z Nat , Z X Y Nat Nat , Nat Nat

X Nat Nat, Y Nat , Nat

— различные решения Γ, t

Упражнение 22.2.3 : Найдите три различных решения для терма

λx :X. λy: Y . λz:Z. ( x z ) ( y z )

в пустом контексте.

22.3. Типизация на основе ограничений

В этом разделе мы представим алгоритм, вычисляющий, исходя из терма t и контекста Γ, набор

ограничений — уравнений между выражениями типа (возможно, с использованием типовых перемен-

ных), — которые должны выполняться в любом решении для Γ, t . Интуиция, лежащая в основе этого

алгоритма, в сущности, та же, что и в основе алгоритма проверки типов; однако новый алгоритм не

проверяет ограничения, а просто записывает их для дальнейшего рассмотрения. Например, если ал-

горитм получает терм-применение t

, где Γ t

: T

и Γ t

: T

, вместо того, чтобы проверить,

Эти определения можно организовать иначе. Прежде всего, можно использовать механизм экзистенциальных уни-

фикандов, предложенный Кирхнером и Жуанно (Kirchner and Jouannaud 1990), вместо отдельных условий новизны в пра-

вилах порождения ограничений на Рис. 22.1. Еще одно возможное улучшение, которое можно найти у Реми (R´emy 1992a,

1992b, полная версия в 1998, Глава 5), — рассматривать сами утверждения о типизации как подлежащие унификации

сущности; начиная с тройки Γ, t, T , где все три компонента могут содержать типовые переменные, мы ищем подстановки

σ, такие, что σΓ σ t : σ T , т. е., подстановки, унифицирующие схему утверждения о типизации Γ t : T.

rev. 104

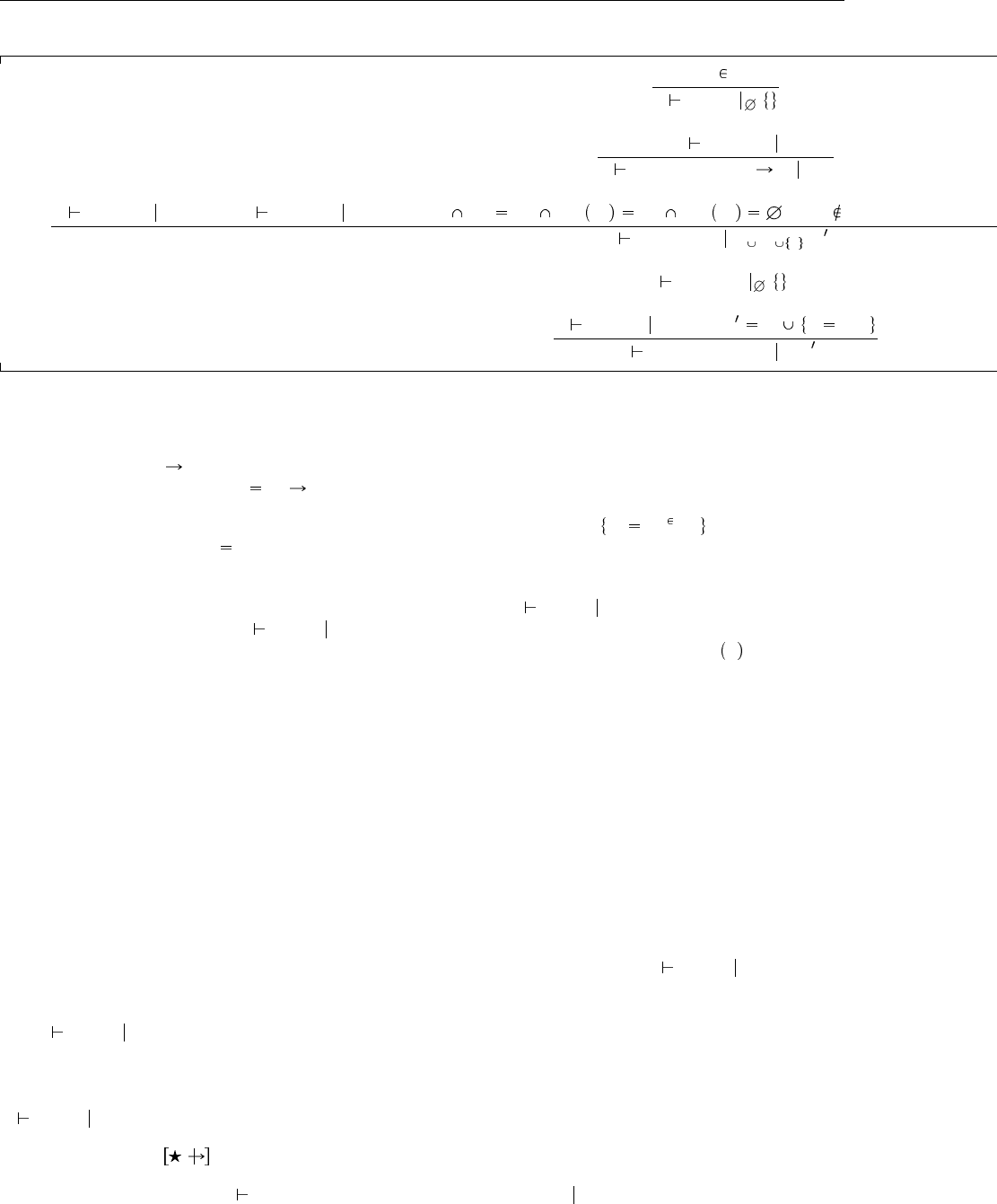
252 22.3. Типизация на основе ограничений

x:T Γ

Γ x : T

(CT-Var)

Γ, x

: T

2 X

Γ λx:T

: T

2 X

(CT-Abs)

Γ t

: T

1 X

Γ t

: T

2 X

F V T

X X

, X

, T

, C

, Γ, t

или t

C C

Γ t

: X

(CT-App)

Γ 0 : Nat (CT-Zero)

Γ t

: T

C C C T Nat

Γ succ t

: Nat

(CT-Succ)

Γ t

: T

C C C T Nat

Γ pred t

: Nat

(CT-Pred)

Γ t

: T

C C C T Nat

Γ iszero t

: Bool

(CT-IsZero)

Γ true : Bool (CT-True)

Γ false : Bool (CT-False)

Γ t

: T

1 X

Γ t

: T

2 X

Γ t

: T

3 X

, X

не пересекаются C C

Bool, T

Γ if t

then t

else t

: T

2 X

(CT-IsZero)

Рис. 22.1. Правила типизации с ограничениями

что T

имеет вид T

, и вернуть T

в качестве типа целого терма, он выбирает новую переменную

X, записывает ограничение T

X, и возвращает X в качестве типа терма-применения.

Определение 22.3.1 Множество ограничений C — это набор уравнений S

i 1..n

. Подстановка σ

унифицирует уравнение S T, если результаты подстановки σS и σT совпадают, Мы говорим, что

подстановка σ унифицирует C (или удовлетворяет ему), если она унифицирует все уравнения в C.

Определение 22.3.2 Отношение типизации с ограничениями Γ t : T

C определяется правилами

на Рис. 22.1. Неформально, Γ t : T

C можно читать как «терм t имеет тип T в контексте

типизации Γ всегда, когда выполнениы ограничения C». В правиле T-App запись F V T обозначает

множество всех типовых переменных, упомянутых в T.

Индексы X помогают отслеживать типовые переменные, введенные в каждом подвыводе. С их помо-

щью мы добиваемся, чтобы новые переменные, введенные в разных поддеревьях, были всегда различны.

При первом прочтении правил можно не обращать внимания на эти индексы и на предпосылки, где они

упоминаются. При следующем чтении обратите внимание, что аннотации и предпосылки обеспечивают

два условия. Во-первых, каждый раз, когда в последнем правиле некоторого вывода выбирается имя

типовой переменной, это имя должно отличаться от имен, упоминающихся в каком-либо из подвыводов.

Во-вторых, когда в правиле упомянуты два или более подвыводов, множества переменных, использу-

емых в этих подвыводах, не должны пересекаться. Заметим также, что эти ограничения не способны

повлиять на нашу способность построить какой-нибудь вывод данного терма; они только запрещают

нам строить выводы, где одна и та же «новая» перемнная вводится в нескольких местах. Поскольку

запас имен типовых переменных бесконечен, нам всегда удастся удовлетворить требование новизны.

При чтении снизу вверх правила типизации с ограничениями определяют несложную процедуру,

которая, принимая на входе Γ и t, вычисляет T и C (а также X ), такие, что Γ t : T

C. Однако

в отличие от обыкновенного алгоритма типизации для простого типизированного лямбда-исчисления,

новый алгоритм никогда не терпит неудачу: для любых Γ и t всегда имеются какие-либо T и C, так

что Γ t : T

C. Более того, T и C однозначно определяются при заданных Γ и t. (Строго говоря,

алгоритм является детерминистским, только если его рассматривать «с точностью до выбора новых

имен типа». Мы вернемся к этому в Упражнении 22.3.9.)

Чтобы разгрузить нотацию в последующих рассуждениях, мы иногда опускаем X и пишем просто

Γ t : T C.

Упражнение 22.3.3 : Постройте вывод типизации с ограничениями, имеющий заключение

λx:X. λy:Y. λz:Z. (x z) (y z) : S

rev. 104

22.3. Типизация на основе ограничений 253

для некоторых S, X и C.

Идея отношения типизации с ограничениями в том, что мы можем проверить, типизируем ли терм

t в контексте Γ, следующим образом: сначала собираем ограничения C, которые нужно удовлетворить,

чтобы t имел тип, и одновременно получаем тип S, содержащий переменные из C, и характеризующий

возможные типы t с точностью до этих переменных. Затем, чтобы найти решения для t, мы просто

ищем подстановки σ, удовлетворяющие ограничениям C (т. е., превращающие все уравнения из C в

тривиальные равенства); для каждой такой σ, тип σS есть возможный тип t. Если мы обнаружим,

что нет подстановок, удовлетворяющих ограничениям C, значит, t невозможно конкретизировать так,

чтобы он стал типизируемым.

Например, множество ограничений, порождаемых алгоритмом для терма t λx:X Y. x 0, равно

Nat Z X Y , а связанный с этим множеством тип результата (X Y) Z. Подстановка σ X

Nat, Y Bool превращает уравнение Nat Z X Y в равенство, и, таким образом, мы видим, что

σ((X Y) Z), т. е., (Nat Bool) Bool, является возможным типом для t.

Эта идея формально выражена в следующем определении:

Определение 22.3.4 Допустим, Γ t : S C. Решением для Γ, t, S, C называется пара σ, T , такая,

что σ удовлетворяет ограничениям C, а σS T.

Алгоритмическая задача поиска подстановок, унифицирующих данный набор ограничений C, будет

рассмотрена в следующем разделе. Однако сначала требуется проверить, что наш алгоритм типизации

с ограничениями дожным образом соответствует изначальному декларативному отношению типизации.

При данных контексте Γ и терме t у нас есть два способа охарактеризовать возможные способы

конкретизации типовых переменных в Γ и t, дающие в результате корректную типизацию:

1. Декларативный как множество всех решений для Γ, t в смысле Определения 22.2.1; либо

2. Алгоритмический через отношение типизации с ограничениями — нужно найти S и C, такие,

что Γ t : S C, а затем взять множество решений Γ, t, S, C .

Мы доказываем эквивалентность этих характеризаций в два шага. Сначала мы показываем, что

всякое решение Γ, t, S, C является также решением Γ, t (Теорема 22.3.5). Затем мы показываем,

что всякое решение для Γ, t можно расширить до решения Γ, t, S, C путем присваивания значений

типовым переменным, введенным в процессе порождения ограничений.

Теорема 22.3.5 Корректность типизиации с ограничениями : Предположим, Γ t : S C.

Если σ, T является решением Γ, t, S, C , то оно также является решением Γ, t .

Для этого направления рассуждений множества новых переменных X несущественны, и их мож-

но опустить.

Доказательство: Индукция по данному нам выводу типизации с ограничениями Γ t : S C. Рас-

сматриваем варианты последнего примененного правила.

Вариант CT-Var: t x x:S Γ C

Дано, что σ, T является решением Γ, t, S, C ; поскольку C пусто, это просто означает, что σS T.

Но тогда по правилу T-Var мы немендленно получаем σΓ x : T, как и требуется.

Вариант CT-Abs: t λx:T

S T

Γ, x:T

: S

Дано, что σ, T является решением для Γ, t, S, C , т. е., σ унифицирует C, а T σS

σT

σS

. Так что σ, σS

является решением Γ, x:T

, t

, S

, C . Согласно предположению ин-

дукции, σ, σS

— решение Γ, x:T

, t

, т. е., σΓ, x:σT

σt

: σS

. По правилу T-Abs, σΓ

λx:σT

.σt

: σT

σS

σ T

T, как нам и требуется.

Вариант CT-App: t t

S X

Γ t

: S

Γ t

: S

C C

По определению, σ унифицирует C

и C

, и σS

σ S

X . Таким образом, σ, σS

и σ, σS

явля-

ются решениями для Γ, t

, S

, C

и Γ, t

, S

, C

. Отсюда по предположению индукции имеем σΓ

σt

: σS

и σΓ σt

: σS

. Однако, поскольку σS

σS

σX, мы получаем σΓ σt

: σS

σX

и, по правилу T-App, σΓ σ t

: σX T.

Остальные варианты:

Аналогично.

rev. 104

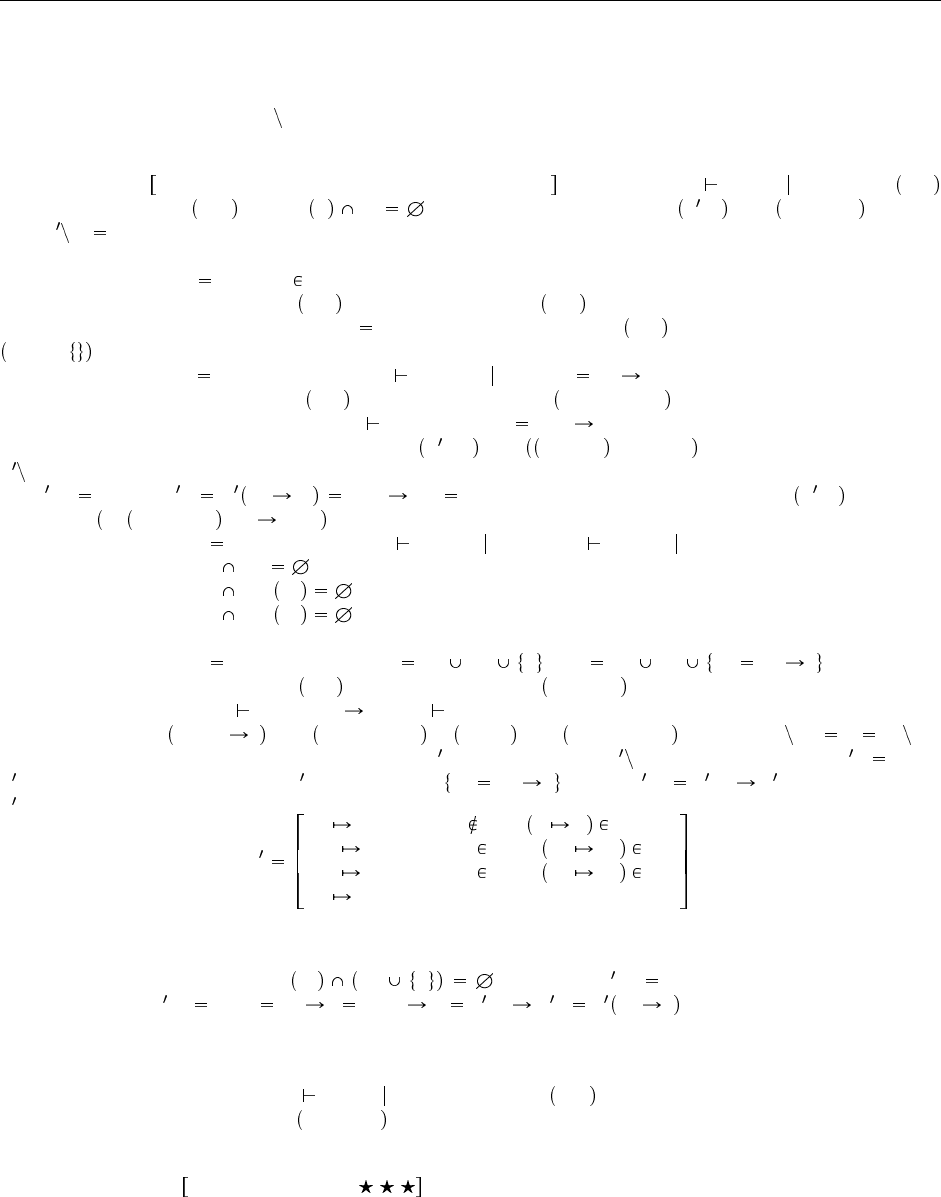
254 22.3. Типизация на основе ограничений

Доказательство полноты типизации с ограничениями по отношению к обыкновенному отношению

типизации несколько сложнее, поскольку нам приходится тщательно отслеживать новые имена типов.

Определение 22.3.6 Запись σ X обозначает подстановку, которая не определена для переменных из

X , а в остальном ведет себя как σ.

Теорема 22.3.7 Полнота типизации с ограничениями : Допустим, Γ t : S

C. Если σ, T

является решением Γ, t , и dom σ X , то существует решение σ , T для Γ, t, S, C , такое,

что σ X σ.

Доказательство: Индукция по данному нам дереву вывода типизации с ограничениями.

Вариант CT-Var: t x x:S Γ

Исходя из предположения, что σ, T является решением Γ, x , лемма об обращении отношения ти-

пизации (9.3.1) говорит нам, что T σS. Но в таком случае, σ, T является также решением

Γ, x, S, .

Вариант CT-Abs: t λx:T

Γ, x:T

: S

2 X

C S T

Исходя из предположения, что σ, T является решением Γ, λx:T

, лемма об обращении отно-

шения типизации дает нам σΓ, x:σT

σt

: T

и T σT

для некоторого T

. Согласно пред-

положению индукции, существует решение σ , T

для Γ, x:T

, t

, S

, C , такое, что подстановка

σ X согласована с σ. При этом X не может включать никакие типовые переменные из T

. Поэто-

му σ T

σT

, а σ S σ T

σT

T. Таким образом, мы видим, что σ , T является

решением Γ, λx:T

, T

, C .

Вариант CT-App: t t

Γ t : S

1 X

Γ t : S

2 X

F V S

X не встречается в X

, X

, S

, C

S X X X

X C C

Исходя из предположения, что σ, T является решением Γ, t

, лемма об обращении отношения

типизации дает нам σΓ σt

: T

T и σΓ σt

: T

. Согласно предположению индукции, суще-

ствуют решения σ

, T

T для Γ, t

, S

, C

и σ

, T

для Γ, t

, S

, C

, причем σ

σ σ

Требуется продемонстрировать подстановку σ , такую, что: (1) σ X согласована с σ; (2) σ X T; (3)

σ унифицирует C

и C

, и (4) σ унифицирует S

X , т. е., σ S

σ S

σ X. Мы определяем

σ так:

Y U если Y X и Y U σ

если Y

и Y

если Y

и Y

X T

Условия (1) и (2) выполняются очевилным образом. (3) выполняется, поскольку X

и X

не пересе-

каются. Для проверки (4) заметим сначала, что дополнительные условия новизны типовых пере-

менных гарантируют нам F V S

X , так что σ S

. Теперь проводим такое

преобразование: σ S

T σ

T σ S

σ X σ S

X .

Остальные варианты:

Аналогично.

Следствие 22.3.8 Допустим, Γ t : S C. Решение для Γ, t существует тогда и только тогда,

когда существует решение для Γ, t, S, C .

Доказательство: Теоремы 22.3.5 и 22.3.7.

Упражнение 22.3.9 Рекомендуется, : В промышленном компиляторе, как правило, вместо

недетерминистского выбора новой типовой переменной в правиле CT-App применялась бы функция,

порождающая новую типовую переменную при каждом своем вызове, отличную от всех остальных

переменных, порождаемых той же функцией при других вызовах, а также от всех типовых пере-

менных, явно упомянутых в контексте проверяемого типа. Поскольку такие глобальные операции

вида «gensym» работают через побочные эффекты и скрытую глобальную переменную, о них трудно

рассуждать формально. Однако из поведение можно сымитировать достаточно точно, и при этом

rev. 104

22.4. Унификация 255

достаточно удобно с математической точки зрения, если «прошить» правила порождения ограни-

чений последовательностью неиспользованных имен переменных.

Пусть F обозначет последовательность неиспользованных имен типовых переменных. Тогда, вме-

сто того, чтобы записывать отношение порождения ограничений как Γ t : T C, мы его записы-

ваем как Γ

t : T

C, где Γ, F и t служат входами алгоритма, а T, F и C — выходами. Каждый

раз, когда алгоритму требуется новая переменная, он отцепляет первый элемент F и возвращает

остаток как F .

Запишите правила этого алгоритма. Докажите, что они эквивалентны, в соответствующем

смысле, исходным правилам порождения ограничений.

Упражнение 22.3.10 Рекомендуется, : Реализуйте алгоритм из Упражнения 22.3.9 на ML. Ис-

пользуйте тип данных

type ty =

Ty Bool

| TyArr of ty * ty

| TyId of string

| TyNat

для типов, и

type constr = ( ty * ty ) list

для множеств ограничений. Кроме того, Вам потребуется представление для бесконечных после-

довательностей новых имен переменных. Есть множество способов организовать такие последова-

тельности; вот достаточно простой, через рекурсивный тип данных:

type nextuvar = N e xtUVar of s tring * uvargenerator

and u v a r g e n e r a t o r = unit -> nextuvar

let uvarg en =

let rec f n () = Next U Var ( " ?X_ " ^ string_of_int n , f (n +1))

in f 0

А именно, функция uvargen, будучи вызвана с аргументом (), возвращает значение вида

NextUVar(x,f), где x — новое имя переменной, а f — еще одна функция такого же вида.

Упражнение 22.3.11 : Покажите, как расширить алгоритм порождения ограничений, чтобы он

мог работать с определениями рекурсивных функций общего вида (§11.11).

22.4. Унификация

При поиске решений для множеств ограничений мы используем идею, высказанную Хиндли (Hindley

1969) и Милнером (Milner 1978) — с помощью унификации (Robinson 1971) убедиться, что множество

решений непусто, и, если это так, найти «наилучший» его элемент, в том смысле, что всякое решение

можно без труда породить из этого.

Определение 22.4.1 Подстановка σ называется менее конкретной (или более обобщенной), чем под-

становка σ , что записывается σ σ , если σ σ γ для некоторой подстановки γ.

Определение 22.4.2 Главным унификатором (иногда говорят наиболее общий унификатор) для мно-

жества ограничений C называется подстановка σ, удовлетворяющая C, если при этом σ σ для

всякой подстановки σ , удовлетворяющей C.

Упражнение 22.4.3 : Выпишите главные унификаторы (там, где они существуют) для следующих

множеств ограничений:

X Nat, Y X X Nat Nat X Y

X Y Y Z, Z U W Nat Nat Y

Y Nat Y (пустое множество ограничений)

rev. 104

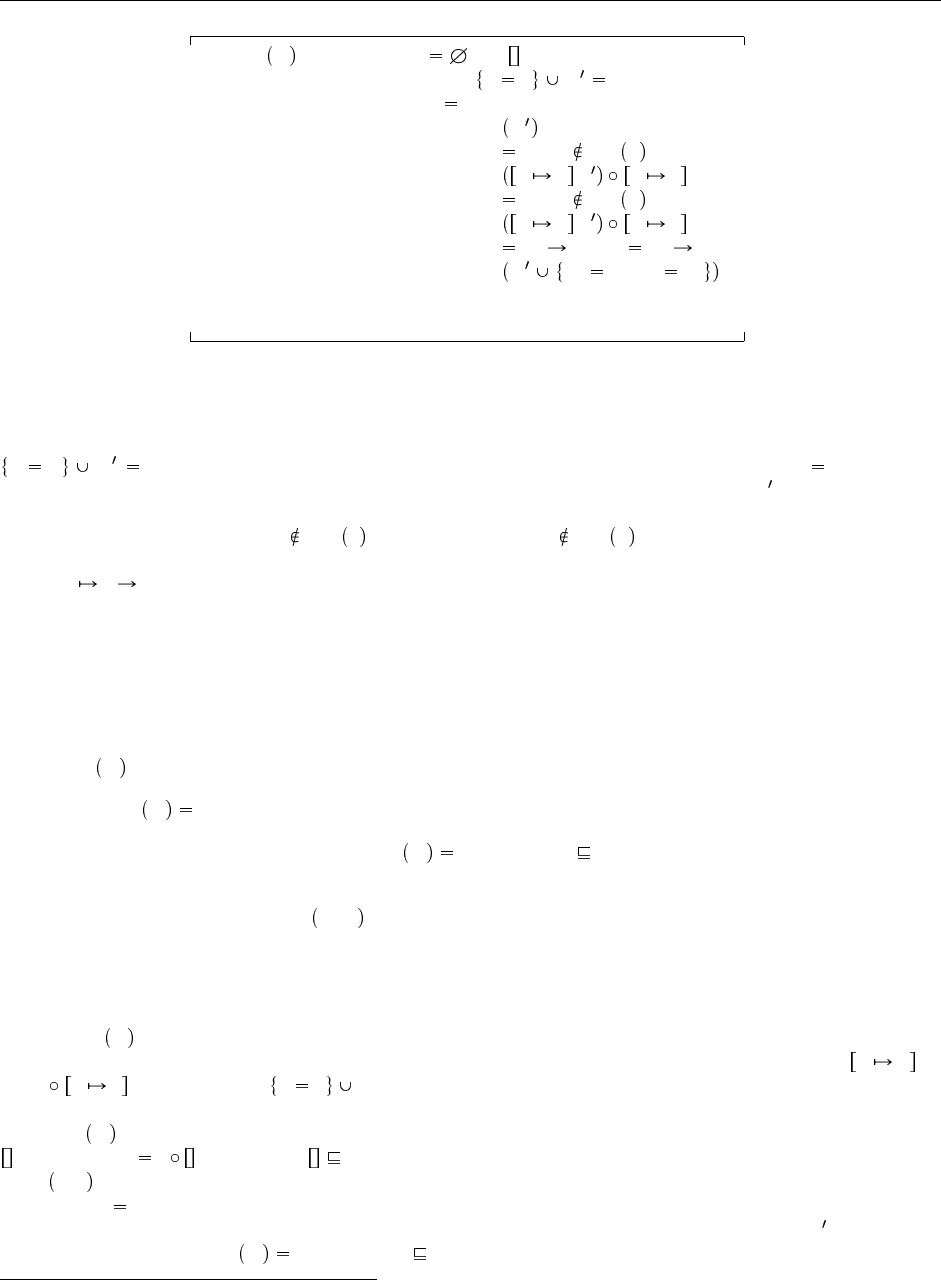
256 22.4. Унификация

unify C = если C , то

иначе пусть S T C C

если S T

тогда unify C

иначе если S X и X F V T

тогда unify X T C X T

иначе если T X и X F V S

тогда unify X S C X S

иначе если S S

и T T

тогда unify C S

, S

иначе

неудача

Рис. 22.2. Алгоритм унификации

Определение 22.4.4 Алгоритм унификации для типов приведен на Рис. 22.2.

Выражение «пусть

S T C C» во второй строке должно читаться как «выберем ограничение S T из набора

ограничений C и обозначим множество оставшихся ограничений в C символом C ».

Дополнительные условия X F V T в пятой строке и X F V S в седьмой известны как провер-

ка на вхождение. Они не дают алгоритму породить решение, содержащее циклическую подстановку

вроде X X X, которая не имеет смысла, если речь идет о конечных выражениях типа. (Если мы

расширим наш язык и включим в него бесконечные выражения типа — т. е., рекурсивные типы, как

они представлены в Главах 20 и 21, — проверку на вхождение можно убрать.)

Теорема 22.4.5 Алгоритм unify всегда завершается. При этом он терпит неудачу, если получает

на входе невыполнимый набор ограничений, а в противном случае возвращает главный унификатор.

Более формально:

1. unify C завершается для любого C, либо неудачей, либо давая в результате подстановку;

2. если unify C σ, то σ — унификатор для C;

3. если δ — унификатор для C, то unify C σ, причем σ δ.

Доказательство: для доказательства пункта (1), определим функцию degree от множества огра-

ничений C, возвращающую пару m, n , где m — число различных типовых переменных в C, а n —

общий размер всех типов в C. Несложно проверить, что всякая ветвь алгоритма unify либо немед-

ленно завершается (успешно в первой ветви и неудачно в последней), либо вызывает unify рекурсивно

с множеством ограничений, чей показатель degree лексикографически меньше исходного.

Часть (2) представляет собой прямолинейную индукцию по числу рекурсивных вызовов при вычис-

лении unify C . Все варианты тривиальны, за исключением двух ветвей, работающих с переменными.

В этих ветвях для доказательства используется наблюдение, что, если σ унифицирует X T D,

то σ X D унифицирует X T D для любого множества ограничений D.

В части (3) доказательство снова ведется индукцией по числу рекурсивных вызовов при вычисле-

нии unify C . Если C — пустое множество, unify немедленно возвращает тривиальную подстановку

; поскольку δ δ , мы имеем δ, как и требуется. Если C непусто, unify выбирает некоторую

пару S, T из C, и рассматривает варианты форм S и T.

Вариант: S T

Поскольку подстановка δ является унификатором для C, она унифицирует также и C . По предпо-

ложению индукции, unify C σ, причем σ δ, как и требуется.

Заметим, что ничто в этом алгоритме не зависит от того факта, что мы унифицируем выражения типов, а не какие-

либо другие выражения; тот же алгоритм можно использовать при решении наборов ограничений для любых выражений

(первого порядка).

rev. 104

22.5. Главные типы 257

Вариант: S X и X F V T

Поскольку δ унифицирует S и T, имеем δ S δ T . Таким образом, для любого типа U выполняется

δ U δ X T U ; в частности, поскольку δ унифицирует C , она также должна унифицировать

X T C . Предположение индукции дает нам unify X T C σ , причем δ γ σ для некоторой

γ. Поскольку unify C σ X T , достаточно показать, что δ γ σ X T . Рассмотрим

любую переменную Y. Если Y X, очевидно, имеем γ σ X T Y γ σ Y δY. С другой

стороны, как мы уже видели, γ σ X T X γ σ T δX. Сочетая эти два наблюдения,

получаем δY γ σ X T Y для всех переменных Y, т. е., δ γ σ X T .

Вариант: T X и X F V S

Аналогично.

Вариант: S S

и T T

Не представляет труда. Достаточно заметить, что δ является унификатором S

C тогда и только тогда, когда она унифицирует C S

, S

Если ни одно из этих условий не применимо к S и T, то unify C терпит неудачу. Но это может

произойти только в двух случаях: либо S равен Nat, а T — функциональный тип (или наоборот), либо

S X и X T (или наоборот). Первый случай явно противоречит предположению, что C унифи-

цируем. Чтобы увидеть, что второй случай также ему противеоречит, заметим, что, по этому

предположению, δS δT; если X встречается в T, то δT всегда будет строго больше, чем δS. Таким

образом, если unify C терпит неудачу, то множество ограничений C не унифицируемо, что про-

тиворечит нашему предположению, что δ является для него унификатором; так что этот случай

не может возникнуть.

Упражнение 22.4.6 Рекомендуется, : Реализуйте алгоритм унификации.

22.5. Главные типы

Мы утверждали выше, что, если существует какой-то способ конкретизировать типовые переменные

в терме так, чтобы он стал типизируемым, то существует и наиболее общий, или главный, способ это

сделать. Теперь мы формализуем это утверждение.

Определение 22.5.1 Главным решением Γ, t, S, C называется такое решение σ, T , что, если σ , T’

также является решением Γ, t, S, C , то выполняется σ σ . Если σ, T — главное решение, то T

называется главным типом терма t в контексте Γ.

Упражнение 22.5.2 : Найдите главный тип λx:X. λy:Y. λz:Z. (x z) (y z).

Теорема 22.5.3 Главные типы : Если задача Γ, t, S, C имеет решение, то она имеет и главное

решение. Алгоритм унификации на Рис. 22.2 позволяет опеределить, имеет ли Γ, t, S, C решение,

и, если оно есть, найти главное.

Доказательство: По определению решения для Γ, t, S, C и свойствам унификации.

Следствие 22.5.4 Задача определить, есть ли решение у Γ, t , разрешима.

Доказательство: По Следствию 22.3.8 и Теореме 22.5.3.

Упражнение 22.5.5 Рекомендуется, , : Сочетайте вместе алгоритмы порождения ограни-

чений из Упражнений 22.3.10 и 22.5.5 и постройте программу проверки типов, вычисляющую главные

типы. За основу можно взять программу reconbase. Типичный протокол взаимодействия с Вашей

программой может выглядеть так:

λx :X. x;

<fun > : X -> X

λz :ZZ . λy: YY . z ( y true );

Не следует путать главные типы с главной типизацией. См. стр. 263.

rev. 104

258 22.6. Неявные аннотации типов

<fun > : (? X

-> ?X

) -> ( Bool -> ?X

) -> ?X

λw :W. if true then false else w false ;

<fun > : ( Bool - > Bool ) -> Bool

Типовые переменные с именами вроде ?X

порождаются автоматически.

Упражнение 22.5.6 : Какие сложности возникают при попытке распространить данные выше

определения (22.3.2 и др.) на записи? Как можно с этими сложностями справиться?

С помощью идеи главных типов можно построить алгоритм реконструкции типов, работающий бо-

лее мелкими шагами, чем описанный здесь. Вместо того, чтобы порождать сначала все ограничения,

а потом пытаться их удовлетворить, можно чередовать порождение и разрешение ограничений, чтобы

алгоритм реконструкции типов на каждом шагу возвращал главный тип. То, что этот тип является

главным, гарантирует нам, что никогда не придется анализировать подтерм повторно: алгоритм всегда

берет на себя наименьшие возможные обязательства, чтобы достичь типизируемости. Существенным

преимуществом такого алгоритма будет, что он намного точнее сможет указывать ошибки в пользова-

тельских программах.

Упражнение 22.5.7 : Модифицируйте свое решение Упражнения 22.5.5, чтобы унификация

проводилась пошагово и возвращались главные типы.

22.6. Неявные аннотации типов

Как правило, языки с поддержкой реконструкции типов позволяют программистам полностью опус-

кать аннотации типов на лямбда-абстракциях. Один из способов достичь этого (как мы заметили в

§22.2) — заставить процедуру синтаксичекого анализа вставлять вместо опущенных аннотаций свеже-

порожденные типовые переменные. Более привлекательным решением будет добавить неаннотирован-

ные абстракции в синтаксис термов, а также ввести в отношение типизации с ограничениями новое

правило:

X X Γ, x:X t

: T

Γ λx.t

: X T

X X

(CT-AbsInf)

Такой подход к неаннотированным абстракциям несколько проще, чем предложение считать их син-

таксическим сахаром. Кроме того, он добавляет выразительности, немного, но с пользой: если мы

скопируем неаннотированную абстракцию несколько раз, правило CT-AbsInf позволит нам выбрать

разные переменные в качестве типов аргумента в каждой копии. Напротив, если мы будем считать,

что «голая» абстракция снабжена невидимой типовой переменной, копирование породит несколько вы-

ражений с одним и тем же типом аргумента. Это различие окажется сущетвенным при обсуждении

полиморфизма через let в следующем разделе.

22.7. Полиморфизм через let

Термин полиморфизм обозначает семейство различных механизмов, позволяющих использовать

один и тот же участок программы с различными типами в различных контекстах (в §23.2 более по-

дробно обсуждается несколько разновидностей полиморфизма). Алгоритм реконструкции типов, при-

веденный выше, несложно обобщить, получая при этом простую форму полиморфизма, называемую

полиморфизм через let (также известный как полиморфизм в стиле ML или полиморфизм по Дамасу-

Милнеру). Такой полиморфизм впервые появился в исходном диалекте ML (Milner 1978) и позднее был

включен во множество удачных языков, где он служит основой мощных обобщенных библиотек часто

используемых структур (списков, массивов, деревьев, хэш-таблиц, потоков, виджетов для взаимодей-

ствия с пользователем, и т. д.).

rev. 104

22.7. Полиморфизм через LET 259

Мотивация для полиморфизма через let происходит из примеров вроде следующего. Допустим, мы

определяем и используем простую функцию double, дважды применяющую свой первый аргумент ко

второму:

let double = λf: Nat -> Nat . λa: Nat . f( f (a )) in

do uble (λx: Nat . succ ( succ x )) 2;

Поскольку мы хотим применять double к функциям типа Nat Nat, мы выбираем аннотацию, сооб-

щающую ей тип (Nat Nat) (Nat Nat). Кроме того, мы можем определить double так, чтобы она

удваивала булевскую функцию:

let double = λf: Bool -> Bool . λa: Bool . f(f( a )) in

do uble (λx: Bool . x ) false ;

Однако мы не можем использовать одну и ту же функцию double как с булевскими значениями, так

и с числами: если в одной и той же программе нам требуется и то, и другое, надо определить две

функции, отличающиеся только аннотациями типов:

let doubleNat = λf: Nat -> Nat . λa : Nat . f( f (a )) in

let doubleNat = λf: Bool - > Bool . λa : Bool . f(f ( a)) in

let a = double N a t (λx : Nat . succ ( succ x )) 1 in

let b = doubleBool (λx: Bool . x ) false in ...

Даже если мы аннотируем абстракцию в double типовой переменной,

let double = λf:X ->X. λa : X. f (f (a )) in

это не поможет. Например, если мы напишем

let double = λf:X ->X. λa : X. f (f (a )) in

let a = double N a t (λx : Nat . succ ( succ x )) 1 in

let b = doubleBool (λx: Bool . x ) false in ...

то вхождение double в определении a породит ограничение X X Nat Nat, а вхождение double в

определении b породит ограничение X X Bool Bool. Эти ограничения выдвигают несовместимые

требования к X, и вся программа оказывается нетипизируемой.

Почему у нас не получилось? Переменная X выступает в этом примере сразу в двух ролях. Во-

первых, она отражает ограничение, что первый аргумент double при вычислении a должен быть функ-

цией, чьи типы аргумента и результата совпадают с типом (Nat) второго аргумента double. Во-вторых,

она отражает ограничение, что аргументы double при вычислении b должны находиться в подобных

же отношениях. К сожалению, поскольку в обоих случаях используется одна и та же переменная X,

возникает ненужное нам ограничение, что вторые аргументы при обоих вызовах double должны быть

одного и того же типа.

Нам хотелось бы разбить эту последнюю связь — т. е., связать различные переменные X с каждым

вызовом double. К счастью, это нетрудно организовать. Первым шагом мы изменяем обыкновенное

правило типизации для let, так что, вместо того, чтобы вычислять тип связываемого значения t

, а

затем использовать его как тип переменной x при вычислении типа тела t

Γ t

: T

Γ, x:T

: T

Γ let x=t

in t

: T

(T-Let)

оно подставляло t

вместо x в тело, а затем проверяло типы в получившемся выражении:

Γ x t

: T

Γ let x=t

in t

: T

(T-LetPoly)

Подобным образом записывается и правило типизации с ограничениями для let:

Γ x t

: T

2 X

Γ let x=t

in t

: T

2 X

(CT-LetPoly)

В сущности, мы изменили правила типизации для let, чтобы они производили шаг вычисления

let x=v

in t

x v

(E-LetV)

прежде, чем определяются типы.

На втором шаге мы переписываем определение double через неявно аннотированные лямбда-

абстракции из §22.6.

rev. 104

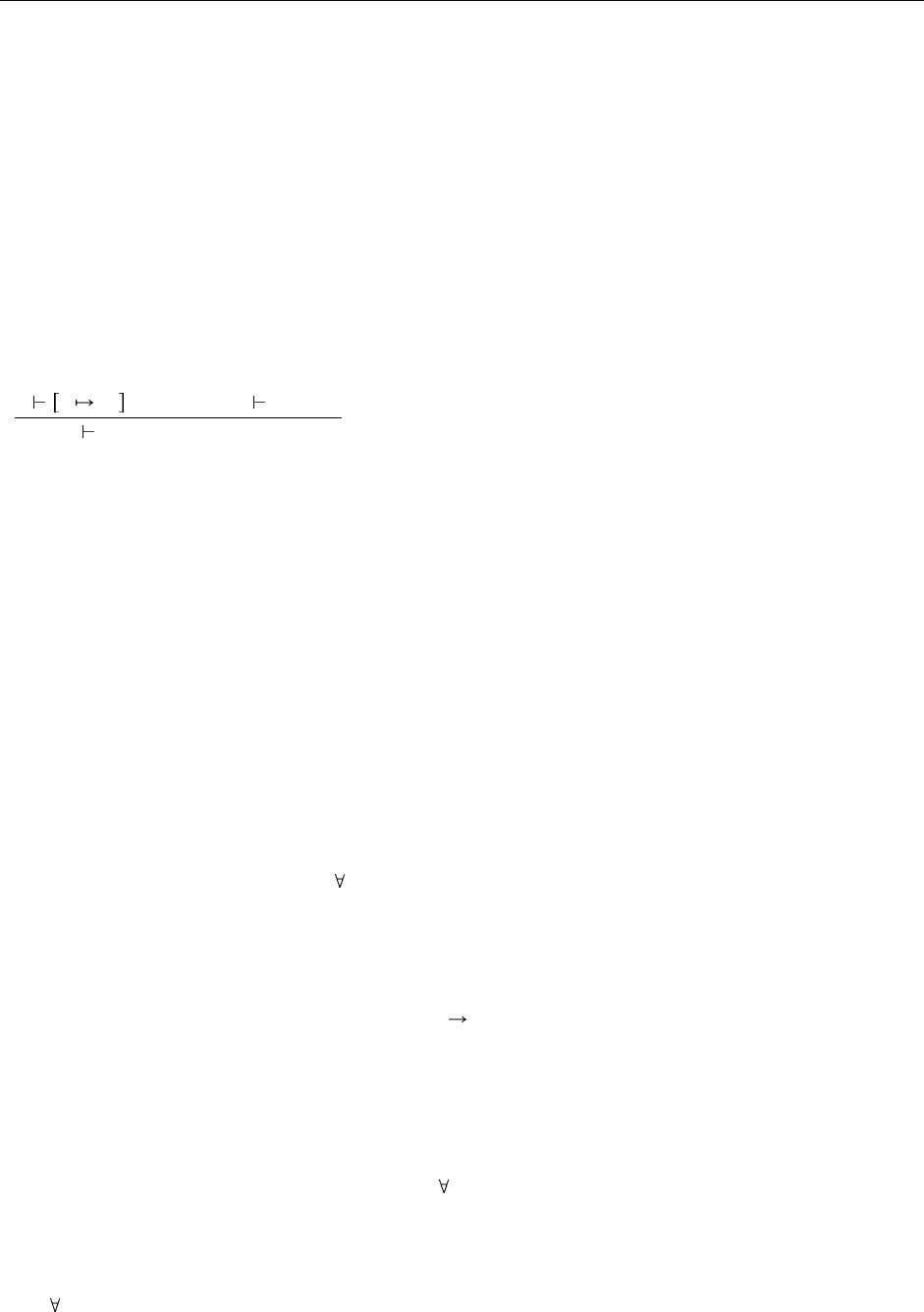
260 22.7. Полиморфизм через LET

let double = λf. λa . f (f (a )) in

let a = double N a t (λx : Nat . succ ( succ x )) 1 in

let b = doubleBool (λx: Bool . x ) false in ...

Сочетание правил типизации ограничениями для let (CT-LetPoly) и неявно аннотированной лямбда-

абстракции (CT-AbsInf) дает нам ровно то, что нужно: CT-LetPoly порождает две копии определе-

ния double, а CT-AbsInf приписывает каждой из абстракций отдельную типовую переменную. Обык-

новенный процесс разрешения ограничений завершает требуемую работу.

Однако у этой схемы есть несколько недостатков, которые нужно исправить, прежде, чем мы сможем

применить ее на практике. Одно очевидное упущение состоит в том, что, если мы ни разу не используем

связанную через let переменную в теле let, определение просто не будет подвергнуто проверке типов.

Например, программа вроде

let x = <бессмыслица> in 5

пройдет проверку. Это можно исправить, добавив предпосылку в правило типизации

Γ x t

: T

Γ t

: T

Γ let x=t

in t

: T

(T-LetPoly)

и соответствующую предпосылку в правило CT-LetPoly, проверяющую, что t

правильно типизиро-

ван.

Близкая по природе проблема состоит в том, что, если тело let содержит несколько вхождений свя-

занной через let переменной, то вся правая сторона определения let будет проверяться при каждом

вхождении, независимо от того, есть ли там неявно аннотированные лямбда-абстракции. Поскольку

сама правая сторона может содержать выражения let, это правило типизации может заставить про-

грамму проверки проделать объем работы, экспоненциально зависящий от размера исходного терма!

Чтобы избежать этих постоянных перепроверок, практические реализации языков с полиморфиз-

мом исползуют несколько более хитрую (но формально эквивалентную) формулировку правил типи-

зации. Вкратце, проверка типов для терма let x=t

in t

в контексте Γ происходит так:

1. С помощью правил типизации с ограничениями мы вычисляем тип S

и множество связанных с

ним ограничений C

для связываемого терма t

2. Запускаем унификацию и находим наиболее общее решение σ для ограничений C

. Применяем σ

к S

и получаем главный тип t

— T

3. Обобщаем остающиеся в T

переменные. Если остаются переменные X

. . . X

, мы записываем глав-

ную схему типа для t

в виде X

...X

. Здесь тонкость состоит в том, что нельзя обобщать

переменные из T

, которые также встречаются в Γ, поскольку этим переменным соответствуют

реальные ограничения, существующие между t

и его окружением. Например, в

λf :X ->X. λx : X. let g=f in g( x );

не следует обобщать переменную X в типе X X, который приписывается терму g, поскольку это

позволило бы нам писать неверные программы вроде

(λf :X ->X. λx : X. let g=f in g (0))

(λx : Bool . if x then true else false )

true ;

4. Расширяем контекст, указывая схему типа X

...X

для переменной x, и начинаем проверять

типы в теле t

. В общем случае, теперь контекст сопоставляет каждой переменной не тип, а схему

типа.

5. Каждый раз, как нам внутри t

встречается переменная x, мы рассматриваем схему ее типа

...X

. Порождаем новые типовые переменные Y

. . . Y

и с их помощью конкретизируем

rev. 104