Петросян Л.А. и др. Теория игр
Подождите немного. Документ загружается.


лишь от производственной программы). Для простоты будем счи-
тать,
что выигрыш центра А
0
удовлетворяет условию
/
0
(*)=
£/(**),
где слагаемое
1(х
к
)
интерпретируется как выигрыш игрока А
0
, полу-
чаемый от игрока В
к
. Предположим также, что /(jt
fc
)^0 для всех
х
к
еВ
к
(и
к
) и 4(0) = 0, /(0) = 0, к=\, ..., п.
Подобно тому как это сделано в
§
5, представим иерархическую
игру п. 6.3 в виде бескоалиционной игры (п+1) лица в нормальной
форме, где стратегиями игрока А
0
будут векторы ие
U,
а стратеги-
ями игроков В
к
— функции из соответствующих множеств. Постро-
им характеристическую функцию »(•) этой игры, следуя
п.
9.2 гл. III.
Для каждого подмножества S игроков
v
(5) будет равно значению
(оно существует в условиях п. 6.3) антагонистической игры между
коалициями S и N\S, в которой выигрыш коалиции S определяется
как сумма выигрышей, принадлежащих множеству S игроков.
Пусть N={A
0
, B
it
.... В
я
}. Тогда
S(A)= sup sup {£['(**)+4(**)]|-
п U-1 )
{ueU:
Y.uk=b}
х
к
еВ
к
{и,д
*-1 *=1 п
Заметим, что для всех Sc{B
lt
.... В
я
}, v(S)=0, поскольку игрок
А
0
всегда может распределить весь ресурс
Ь
среди членов коалиции
N\S, в которую он входит, лишив, таким образом, коалицию
S ресурсов (т. е. А
0
всегда может положить
и
к
=0
для
k:B
k
eS,
что
приводит к В
к
(0) = 0 для всех
B
k
eS).
Рассуждая аналогично, имеем
v(A
o
)=0, поскольку игроки B
V
....
В„
всегда могут сделать выигрыш
центра А
0
равным нулю, полагая х*=0 для к=
1,
..., и (не производя
продукции). В том случае, когда коалиция S содержит центр А
0
,
очевидно, что А
0
будет распределять весь ресурс среди членов
коалиции. Это соображение приводит к следующей формуле:
Z(S)= sup sup J £ [l(x
k
)+l
k
(x
k
)]\
{ueU: Z
«*=*}
x
k
eB
k
(u
k
) ^k:B
k
eS
J
k-B
k
eS k:B
k
eS
для
S:A
0
eS.
Можно показать, что при таком определении характеристичес-
200

кой функции С-ядро множества дележей
п
а =
(ос
0
,
а
15
..., а„):а,^0, г'=0, 1, ..., п, £ a,=«(JV)
1 = 0
всегда непусто.
6.4. Иерархические системы с подразделениями двойного подчи-
нения называются ромбовидными (рис. 21). Управление подраз-
деления двойного подчинения С зависит от управления В± и от
управления i?
2
. Можно представить ситуацию, в которой центр B
v
представляет интересы отрасли, а В
2
— региональные интересы,
включающие вопросы охраны окружающей среды. Простая ром-
бовидная система управления является примером иерархической
системы с тремя уровнями принятия решений. На высшем уровне
находится административный центр, располагающий материальны-
ми и трудовыми ресурсами. Он воздействует на деятельность двух
подчиненных ему центров, принадлежащих следующему уровню.
От решений, принимаемых этими центрами, зависит объем произ-
водства предприятия, находящегося на последнем уровне иерар-
хической системы.
Будем рассматривать этот процесс принятия решений, как неко-
торую игру четырех лиц. Обозначим ее через Г. Переходя к игровой
постановке, условимся считать, что на 1-м шаге ходит игрок А
0
и выбирает элемент (стратегию)
u =
{u
lt
и
2
) из некоторого множест-
ва U, где U — множество стратегий игрока А
0
. Элемент
и
е U
ограничивает возможности выборов игроков В
х
и В
2
на следующем
шаге. Другими словами, множество выборов игрока
В±
оказывается
функцией параметра u
t
(обозначим его через B
t
(uj), и, аналогично,
множество выборов игрока В
2
оказывается функцией параметра и
г
(обозначимего через
В
2
(и
2
)).
Через co^sB^(u
x
) исо
2
еВ
2
(и
2
) обозна-
чим элементы множества выборов игроков В
1
и В
2
соответственно.
Параметры
оз^
и
со
2
,
выбираемые игроками
В±
и В
2
, задают ограни-
чения на множество выборов игрока С на 3-м шаге игры, т. е. это
множество оказывается функцией параметров со
1
и ш
2
. Обозначим
его через С (со
и
со
2
), а элементы этого множества (производствен-
ные программы) — через «.
Пусть выигрыши всех игроков А
0
, B
lt
B
2
,
С зависят только от производственной про-
граммы v, выбираемой игроком С, и равны
соответственно l
Y
(v), l
2
(v),
l
3
(v),
/
4
(v),
где
Такую иерархическую игру можно предста-
вить как бескоалиционную игру четырех лиц
в нормальной форме, если считать стратеги-
ями игрока А
0
элементы и=(и
1
, м
2
)е U, а стра-
тегиями игроков B
v
B
2
и С — функции
со^
(м
х
),
а>
2
(и
2
)
uvico^ ю
2
) со значениями в множествах
201

В
1
(и
1
), В
2
(и
2
),
С{wу, со
2
) соответственно (обозначим множества
таких функций через В
1;
В
2
, Q, которые каждому возможному
выбору игрока (или игроков), находящегося на более высоком
уровне, ставят в соответствие выбор данного игрока. Полагая
К,(и,
Шу(),
ш
2
(), »(•))«/((«((»!(иД
со
2
(и
2
)),
i=lA,
получим нормальную форму игры Г
Г =
(С7.
В
15
В
2
, С, K
lt
К
2
, К
ъ
, К
4
).
6.5.
Будем искать ситуацию равновесия по Нэшу в игре Г. Для
этого выполним вспомогательные построения.
Для каждой фиксированной пары (ш
15
со
2
), (eo
ls
со
2
) е (J
B
x
(иу)
х
В
2
(и
2
)
обозначим через
v*
(coy,
со
2
)
решение параме-
ueU
трической экстремальной задачи
max /
4
(v)=/
4
(«*
(со!,
оо
2
))- (6-6)
«бС(а>,,й)
3
)
(Считаем, что максимум в (6.6) достигается.) Решение «*(•)=«* (со
у,
со
2
)
задачи (6.6) оказывается функцией параметров со,,
а>
2
и
v*
()е С.
Рассмотрим вспомогательную параметрическую (с параметрами
ы
1(
и
2
) неантагонистическую игру Г'(и
1#
M
2
)
=
{BI(«I)> Вг("Д '2- 'з}
двух лиц
By
и
2?
2
,
где /
2
= /
2
(«*
(со
у,
со
2
)),
/
3
=
/
3
(«*
(Шц
со
2
)).
Стратеги-
ями игрока
.#!
в Г'(«
1
, и
2
) являются элементы
coy
el^ («Д стратеги-
ями В
2
— элементы со
2
еВ
2
(ы
2
). Предположим, что в игре Г'(иу, и
2
)
существует ситуация равновесия по Нэшу, которую обозначим
(co*(uy),
cof(u
2
)). Отметим, что со?() является функцией параметра
MiHco.QeB,, i=l,2.
Пусть, далее,
и*
=
(и*,
и*) — решение следующей экстремальной
задачи:
max ly{v*(a>t(иД
со?
(и
2
))).
(6.7)
ueV
Лемма.
Совокупность
(и*,
cof(),
со*(),
«*(•))
является
ситуаци-
ей равновесия
по Нэшу в игре Г.
Доказательство. Согласно определению и* из (6.7) следует
соотношение
Ку(и*,
cof
Q, ш?(), v*(.))=maxly(v*(cof(11Д a>J(u
2
)))>
^/
х
(•• (mf (иД со?(и
2
)))=^
(и.
o)f Q, со?(.),
«*
(•))
для всех
и
е
U.
Поскольку
cof
(uf),
cof (и*)
образуют ситуацию равно-
весия по Нэшу во вспомогательной игре Г'(м|,
и*
2
),
для любой
функции соу()еВу, сОу(и*) =
сЪуеВу(и*)
выполняются соотношения
К
2
(и*.
шГ(•), <»?(•),
v*(.))
=
l
2
(v*(cof(uf), cof(uf))>
202

>/
2
(«•(&!,
«
2
*(K
2
*)))
=
*
2
(U*,
Ш1
(.),
0*0,
»•(•))•
Аналогичное неравенство справедливо и для игрока В
г
.
По определению функции v* из (6.6) имеем:
К
4
(
М
*,
cof
О, а>?0, »*0)=/4(»'К(4 о*
(»<?)))
=
max /
4
(«)
> /
4
(v)
=
*
4
(и*.
cof
(•), со?
(.),
«
(•))
t;eC(cu*(«f),cu*(«J))
для любой функции i;()eC, v(cof(uf), cof(uf))=veC(cof(uf),
co?(uf)).
Лемма доказана.
6.6 Применяя максиминный подход, для каждой коалиции
5с {А
0
, B
v
B
2
, Q определим v'(S) как наибольший гарантирован-
ный выигрыш S в антагонистической игре между коалицией S,
выступающей в качестве максимизирующего игрока, и коалицией
S'
=
{A
0
, B
V
В
г
C}\S. Предположим, что существует такое
v
0
e(дсо^
со
2
)
для всех ш
15
со
2
,
что
/,(«
0
)
= 0, /=1, 2, 3, 4.
Будем различать два вида коалиций:
\)S:C$S;2)S:CeS.
В первом случае Sa{A
0
, B
v
B
z
) и игрок С, являющийся членом
коалиции N\S, может выбрать стратегию v
o
:/f(v
o
) = 0, i=l, 2, 3, 4,
поэтому v'(S)=0.
Во втором случае определим характеристическую функцию v (S)
следующими равенствами:
а) S=
{С}
v'(S)=min min min max /
4
(«)
uet/
a^eB,^,)
ш
2
еВ
2
(и
2
)
DEC(cD
lt
<U2)
(здесь и далее предполагаем, что все max и min достигаются);
б) S={A
0
, С)
i/(S)=max min min max (/
x
(«)
+ /
4
(«));
net/
а^еВДи,)
<D
2
EB
2
(U
2
)
oeCCtBi.a)!)
в)5={5
1(
С}
t/(S)=min max min max (l
2
(
v
) + U(
v
))'>
ueU
<U,EB,(U,)
<B
2
eB
2
(u
2
)
геС^.ш^
r)S={B
2
,C}
v'(S)=min max min max
(/
3
(«)
+
/
4
(«));
net/
«UJEBJ^J
ш,бВ,(и,)
»еС(ш,,ш
2
)
д) 5=^,52, С}
4
v'(S)=min max max max £
№)'>
ueU
<u,6B,(u,)
ш
2
еВ
2
(ц
2
)
»6C(m„a)j)
,-_
2
е)5={Л
0
.^1.
С}
203

v'(S)—ma\ max min max £
/,(»);
ж)5={Л
0
, ^
2
. С}
v'(S)=max max min max J]
/,(«);
«et/ OjeBjCuj) o^Bjfu,) oeCfOj.ojj) f„i 3 4
3) S={A
0
, B
v
B
2
, C}
4
«'(S^max max max max У
/,(«).
иб17 ш,еВ,(и,) eu
2
eB
2
(u
2
) oeCCo^.CDj) ,-
=
|
При таком определении характеристическая функция обладает
свойством супераддитивности, т. е. для любых S, Ra {А
0
, В
у
, В
г
, С},
для которых Sf]R=0, имеет место неравенство
v(S{]R)>v(S)+v(R).
§ 7. МНОГОШАГОВЫЕ ИГРЫ С НЕПОЛНОЙ
ИНФОРМАЦИЕЙ
7.1.
В §
1
— 4 рассматривались многошаговые игры с полной
информацией, определенные на конечном древовидном графе
Сг=(Х, F), в которых каждый из игроков в момент совершения
своего хода точно знал, в какой позиции или
в
какой вершине дерева
он находится. Именно поэтому удалось ввести понятие стратегии
игрока /как однозначной функции u
t
(x), определенной на множестве
очередности X
t
со значениями в множестве F
x
. Однако если попы-
таться исследовать многошаговую игру, в которой игроки при
совершении своих выборов не знают точно позиции, в которой они
совершают ход, или могут лишь предполагать, что эта позиция
принадлежит некоторому подмножеству А множества очередности
X
h
то реализация стратегии игрока как функции от позиции хеХ,
окажется невозможной. Таким образом, желание усложнить инфор-
мационную структуру игры неизбежно приводит к изменению поня-
тия стратегии. Для точных формулировок необходимо в первую
очередь формализовать понятие информации в игре. Важную роль
здесь играет понятие информационного множества. Проиллюст-
рируем это на нескольких простейших, ставших классическими
в учебной литературе по теории игр примерах [9].
Пример 6.
(Игра
антагонистическая).
Делая 1-й ход, игрок 1 вы-
бирает число из множества
{1, 2}.
Второй ход делает игрок 2. Зная
выбор игрока
1,
он выбирает число из множества
{1, 2}.
Третий ход
опять делает игрок 1. Зная выбор игрока 2 и помня свой выбор, он
выбирает число из множества {1, 2}. На этом игра прекращается,
и игрок 1 получает выигрыш Н (игрок 2 — выигрыш (—Н), т. е.
204
-з -2 г -5 « / / 5
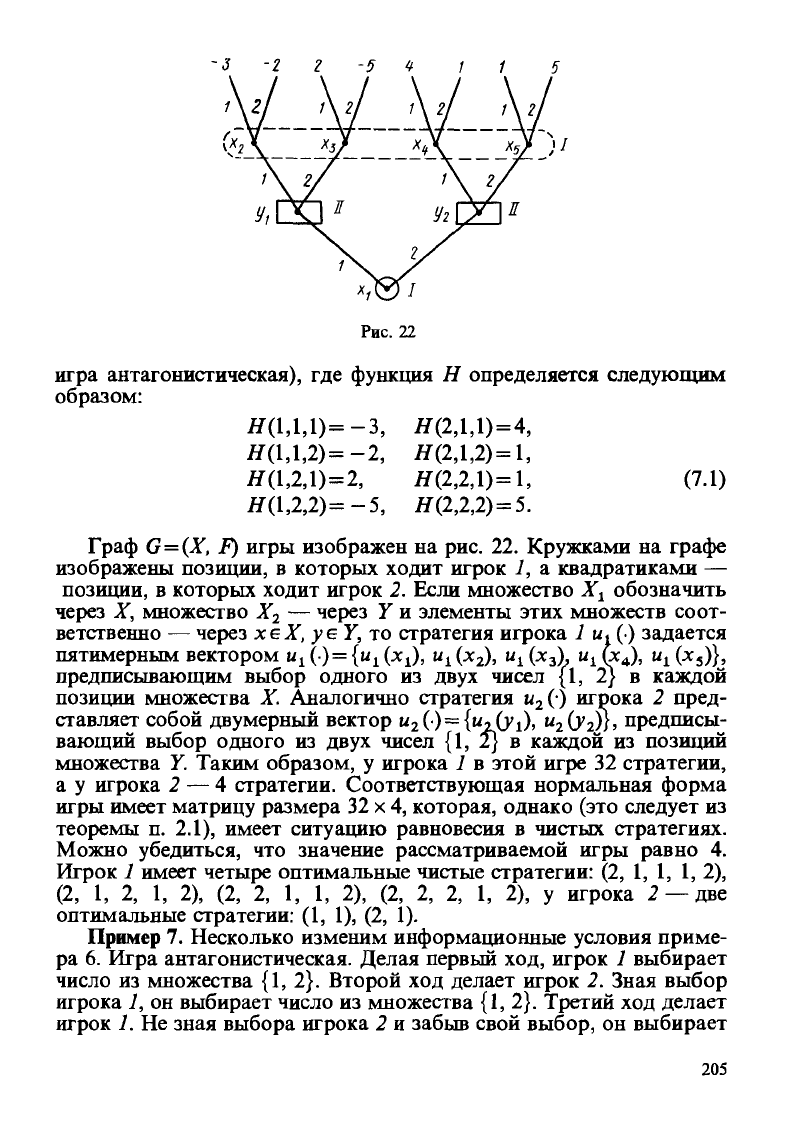
Рис. 22
игра антагонистическая), где функция Я определяется следующим
образом:
Я(1,1,1)=-3,
Я(2,1,1) = 4,
Я(1,1,2)=-2, Я(2,1,2) = 1,
Я(1,2,1) =
2,
Я(2,2,1)=1, (7.1)
Я(1,2,2)=-5,
Я(2,2,2) = 5.
Граф
G =
(X, F) игры изображен на рис. 22. Кружками на графе
изображены позиции, в которых ходит игрок 1, а квадратиками —
позиции, в которых ходит игрок 2. Если множество Х
х
обозначить
через X, множество Х
2
— через Y и элементы этих множеств соот-
ветственно — через х е X, у е Y, то стратегия игрока 1 ы, (•) задается
пятимерным вектором и
1
(•)= {и
х
(x
t
), u
t
(x
2
), u
v
(х
3
), и
к
(х
А
), и
г
(х
5
)},
предписывающим выбор одного из двух чисел {1, 2} в каждой
позиции множества X. Аналогично стратегия ы
2
() игрока 2 пред-
ставляет собой двумерный вектор «
2
(')=
:
{MI(}'I),
"гСУг)}'
предписы-
вающий выбор одного из двух чисел {1, 2} в каждой из позиций
множества У. Таким образом, у игрока 1 в этой игре 32 стратегии,
а у игрока 2 — 4 стратегии. Соответствующая нормальная форма
игры имеет матрицу размера 32 х 4, которая, однако (это следует из
теоремы п. 2.1), имеет ситуацию равновесия в чистых стратегиях.
Можно убедиться, что значение рассматриваемой игры равно 4.
Игрок 1 имеет четыре оптимальные чистые стратегии: (2, 1, 1, 1, 2),
(2,
1, 2, 1, 2), (2, 2, 1, 1, 2), (2, 2, 2, 1, 2), у игрока 2 — две
оптимальные стратегии: (1, 1), (2, 1).
Пример 7. Несколько изменим информационные условия приме-
ра 6. Игра антагонистическая. Делая первый ход, игрок 1 выбирает
число из множества {1, 2}. Второй ход делает игрок 2. Зная выбор
игрока 1, он выбирает число из множества
{1,
2}. Третий ход делает
игрок /. Не зная выбора игрока 2 и забыв свой выбор, он выбирает
205

Рис.23
число из множества {1, 2}. На этом игра прекращается и выигрыш
определяется по формуле (7.1), так же как и в игре примера 6.
Граф
G =
(X,F) игры не изменяется, однако, находясь в узлах х
2
,
х
ъ
,
х^., х
5
(на 3-м ходе игры), игрок 1 не может определить, в каком
из этих узлов он на самом деле находится, но, зная очередность
хода (3-й ход), он может быть уверен, что не находится в узле x
t
. На
графе G мы обведем узлы х
2
, х
3
, х±, х
5
пунктирной линией (рис. 23).
В результате узел х
х
оказался обведенным кружком, что можно
интерпретировать как точное знание игроком 1 этого узла, когда он
в нем находился. Узлы y
lt
у
г
обведены квадратиками, что также
означает, что игрок 2, находясь в одном из них, при совершении
своего хода может отличить его от другого. Объединяя узлы
х
г
,х
г
,
х
4
, х
ь
в одно множество, мы иллюстрируем факт их неразличимо-
сти для игрока 1.
Множества, на которые разбиты узлы, будем называть инфор-
мационными множествами.
Перейдем теперь к описанию стратегий. Состояние информации
игрока 2 не изменилось, поэтому множество его стратегий то же,
что и в примере 6, т. е. оно состоит из четырех векторов (1, 1), (1, 2),
(2,
1), (2, 2). Информационное состояние игрока 1 изменилось. На
3-м шаге игры он знает лишь номер этого шага, но не знает
позиции, в которой находится. Следовательно, он не может ре-
ализовать выбор следующей вершины (или выбор числа из множе-
ства {1, 2}) в зависимости от позиции, в которой находится на
третьем шаге. Поэтому на 3-м шаге ему остается независимо от
в действительности реализовавшейся позиции выбирать одно из
двух чисел {1, 2}. Поэтому его стратегия представляет собой пару
чисел
(г,/),
ге{1, 2},je{l, 2}, где число i выбирается в позиции x
t
,
а число j на 3-м шаге одинаково во всех позициях х
2
, х
ъ
, х
А
, х
5
.
Таким образом, выбор числа j оказывается функцией множества
206

и может быть записан как и {х
2
, х
3
, л;
4
, х
5
} =j. В данной игре у обоих
игроков по четыре стратегии и матрица игры имеет вид
(1.1) (1.2) (2.1) (2.2)
(1.1) Г -3 -3 2 2П
(1.2) -2 -2 -5 -5
(2.1) 4 14 1
(2.2) [15 15
В этой игре нет ситуации равновесия в чистых стратегиях. Значе-
ние игры равно 19/7, оптимальная смешанная стратегия игрока
1 есть вектор (0, 0, 4/7, 3/7), а оптимальная смешанная стратегия
игрока 2 равна (4/7, 3/7, 0, 0). По сравнению с примером 6 гаран-
тированный выигрыш игрока 1 уменьшается. Это вызвано ухудше-
нием его информационного состояния.
Интересно заметить, что матрица игры примера 7 имеет размер
4 х 4, в то время как матрица игры примера 6 имеет размер 32 х 4.
Таким образом, уменьшение доступной информации уменьшает
размер матрицы выигрышей, следовательно, и облегчает решение
самой игры, что противоречит распространенному мнению о том,
что уменьшение информации приводит к усложнению принятия
решений.
Изменяя информационные условия, можно получить другие ва-
рианты игры, описанной в примере 6.
Пример 8. Делая первый ход, игрок 1 выбирает число из множе-
ства
{1,2}.
Второй ход делает игрок 2, который, не зная выбора
игрока 1, выбирает число из множества {1, 2}. Далее, совершая 3-й
ход, игрок 1 выбирает число из множества
{1,
2}, зная выбор игрока
2 и помня свой выбор на первом шаге. Выигрыш определяется так
же,
как и в примере 6 (рис. 24). Поскольку при совершении третьего
хода игрок знает позицию, в которой он находится, позиции третье-
го уровня обведены кружками, два узла, в которых ходит игрок 2,
Рис.
24
207

-з -г г -5 ч ii 5
Рис.
25
мы обвели штриховой линией, включив их в одно информационное
множество.
Пример 9. Делая первый ход, игрок 1 выбирает число из множе-
ства {1, 2}. Второй ход делает игрок 2, не зная выбора игрока /.
Далее, совершая третий ход, игрок 1 выбирает число из множества
{1, 2},
не зная выбора игрока 2 и не помня свой выбор на 1-м шаге.
Выигрыш определяется так же, как в игре из примера 6 (рис. 25).
Здесь стратегия игрока 1 состоит из пары чисел
(г,
j), где /-выбор
на 1-м шаге, a.j — на 3-м шаге игры. Стратегия игрока 2 есть выбор
числа j на 2-м шаге игры. Таким образом, у игрока 1 — четыре
стратегии, а у игрока 2 — две стратегии. Игра в нормальной форме
имеет матрицу размера 4x2:
1 2
(1.1)
Г —3
21
(1.2) -2 -5
(2.1) 4 1 .
(2.2) [ 1 5
Значение игры равно 19/7, оптимальная смешанная стратегия
игрока 1 (О, 0, 4/7, 3/7), оптимальная стратегия игрока 2 (4/7, 3/7).
В этой игре значение оказалось таким же, как и в игре из
примера 7, т. е. оказалось, что ухудшение информационных условий
игрока 2 не улучшило состояние игрока 1. Это обстоятельство
в данном случае носит случайный характер и вызвано спецификой
функции выигрыша.
Пример 10. В предыдущем примере игроки не различают пози-
ции, находящиеся на одном уровне дерева игры, однако они все-
таки знают, какой ход совершают. Можно построить игру, в кото-
рой игроки проявляют большее незнание.
Рассмотрим антагонистическую игру двух лиц, в которой игрок
1 — один человек, а игрок 2 — команда из двух человек А и В. Все
трое изолированы друг от друга (находятся в изолированных поме-
208
щениях) и не могут общаться между собой. В начале игры посред-
ник входит в помещение, где находится игрок 1, и предлагает ему
выбрать число из множества {1, 2}. Если игрок 1 выбирает 1, то
посредник заходит сначала в помещение, где находится А, и пред-
лагает ему выбрать число из множества {1, 2}, затем заходит
к В и предлагает ему сделать выбор из множества {1, 2}. Если же
игрок 1 выбирает 2, то посредник предлагает игроку В сделать
выбор первому. После того как три числа выбраны, игрок 1 выиг-
рывает величину К(х, у, z), где х, у, z — выборы игрока 1 и членов
команды 2 А и В соответственно. Функция К(х, у, z) определяется
следующим образом:
*(1,1,1)=1,
*(1,2,1) =
7,
*(2,1,1) =
5,
*(2,2,1)=6,
*(1,1,2) =
3,
*(1,2,2) =
9,
К (2,1,2)=
1,
* (2,2,2) =
7.
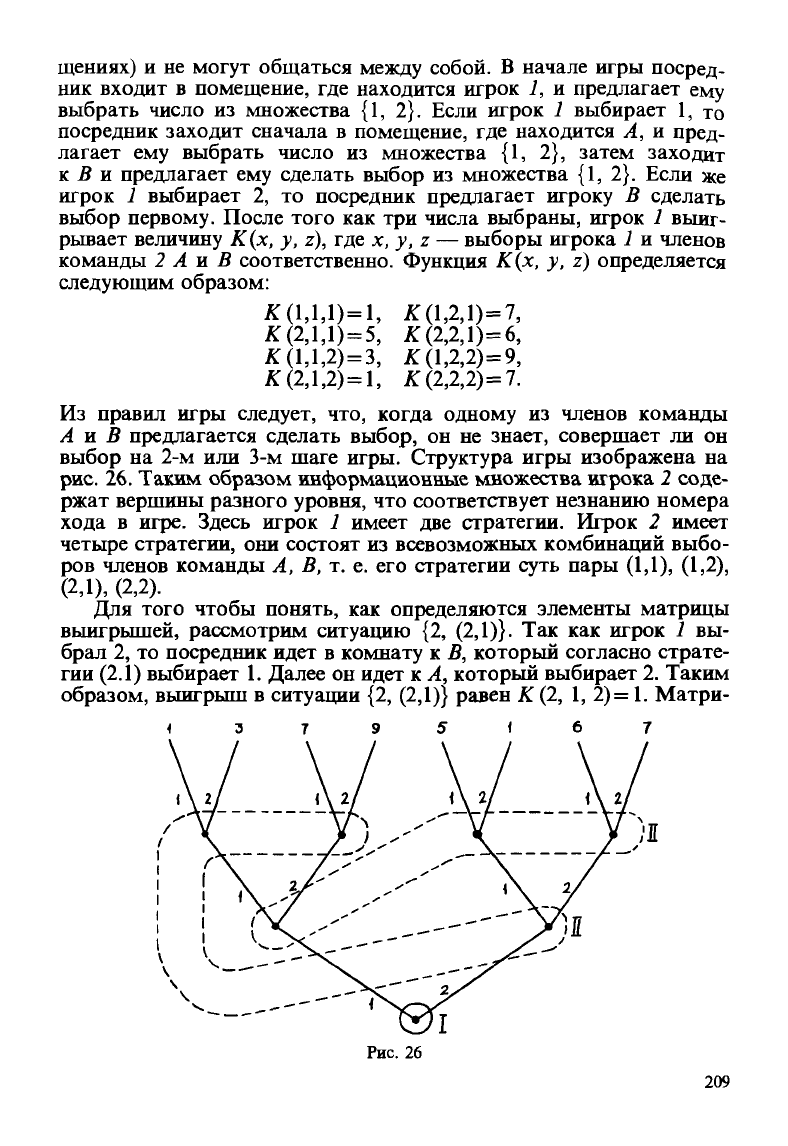
Из правил игры следует, что, когда одному из членов команды
А и В предлагается сделать выбор, он не знает, совершает ли он
выбор на 2-м или 3-м шаге игры. Структура игры изображена на
рис.
26. Таким образом информационные множества игрока 2 соде-
ржат вершины разного уровня, что соответствует незнанию номера
хода в игре. Здесь игрок 1 имеет две стратегии. Игрок 2 имеет
четыре стратегии, они состоят из всевозможных комбинаций выбо-
ров членов команды А, В, т. е. его стратегии суть пары (1,1), (1,2),
(2Д),
(2,2).
Для того чтобы понять, как определяются элементы матрицы
выигрышей, рассмотрим ситуацию {2,
(2,1)}.
Так как игрок ) вы-
брал 2, то посредник идет в комнату к В, который согласно страте-
гии (2.1) выбирает 1. Далее он идет к А, который выбирает
2.
Таким
образом, выигрыш в ситуации {2, (2,1)} равен К
(2,
1, 2)=
1.
Матри-
Рис.
26
209
