Петросян Л.А. и др. Теория игр
Подождите немного. Документ загружается.


Таким образом «монопольное» положение главного игрока
обеспечивает ему в (и
—
1)(и —2)/2
раз больший выигрыш, чем «рядо-
вым» участникам игры.
10.8.
Пример 21 [2].
(«Помещик
и
батраки».)
Предположим, что
имеются
п—
1
батраков (игроки /=1, ..., и—1) и помещик (игрок и)
и что помещик, наняв k батраков, получит от урожая доход f(k)
(f(k) — монотонно возрастает), а батраки сами дохода получить не
могут. Это описывается следующей характеристической функцией:
(0,
в противном случае.
Здесь для всех
7Ъ{л},
|Т|>1,
v(T)-v(T\{n})=f(t-\), где
t=\T\,
и из (10.7) следует
Ф»И=£С.-1 ; Д'-1)=- I /0).
t-2
nl
п
Г-1
На основании условия эффективности и симметрии всех батраков
<РМ=—
Л
(Ди-1)-
1
"l ЛОХ '=1, -,
"-1-
я-1 л ,_,
Упражнения • задачи
1.
Два объединения производят разведку полезных ископаемых на л месторож-
дениях. Фонды средств на разведку у 1-го и 2-го объединения составляют а и /? соот-
ветственно. Прибыль от добычи полезных ископаемых на >-м месторождении равна
у,->0,
она распределяется между объединениями пропорционально доле средств,
которые они вложили в i месторождение. При этом если в i месторождение обоими
не вложено никаких средств, то и прибыли, полученные обоими объединениями на
i-м месторгждении, также равны нулю.
а.) Спи ать указаний конфликт в виде игры двух лиц, считая выигрышем каж-
дого объединения суммарную прибыль, полученную от добычи полезных ископа-
емых на всех месторождениях.
б) Найти ситуацию равновесия по Нашу.
Указание. Воспользоваться вогнутостью функций Н
1
по х и Н
2
по у.
2.
В экологически значимом районе имеется л промышленных предприятий, на
каждом из которых один источник загрязнения. Значение концентрации q
t
вредной
примеси, выбрасываемой i-м предприятием, пропорционально величине выброса
0<x,<a„
i
= l л, этого предприятия. Потери 1-го предприятия складываются из
расходов на переработку отходов производства
(/1(х,))
и налога за загрязнение,
который пропорционален суммарной концентрации q вредной примеси от выброса
всех предприятий. Величина в не должна превышать q— значения предельно до-
пустимой концентрации вредной примеси. В противном случае 1-е предприятие
дополнительно платит штраф 5,-.
Описать указанный конфликт в виде бескоалиционной игры л лиц, считая
проигрышем каждого предприятия суммарные затраты на природоохранные мероп-
риятия.
170

Указание. Воспользоваться результатом примера 5 п. 1.4.
3.
Найти множества всех ситуаций равновесия по Нэшу (в чистых стратегиях)
в следующих
(/и
х
л)-биматричных играх с матрицами А =
{а,^}
и В=
{/?,;/}.
а) Матрицы А и В
—
диагональные и положительные, т. е. т=п, (*{/=/?;,=О, i?j
я а„>0,
Ри>0,
1
=
1,
..., m,j=\, ..., л.
б)
в)
л.\
г
'
5
1, в.?
г
'I;
|_2 2 3j L0 7 8 J
[
3 8 -1"1 Г1 3 4"|
4
0 2 I В= 2 1 8 I
12 3j L2 3 oj
4.
Показать, что в биматричной игре с матрицами
А =
[
1 2 0~| П 4 0"|
13 1, В= 1 3 2
2 2 lj l_l 3 0_|
ситуация
(2,
2) является равновесной. Является ли она сильно равновесной?
5.
В биматричной игре с матрицами
А =
[
4 1 0~| ГО 5 6~|
2 7 5 I В=\ 7 0 2
6 0 1J |_2 6 1_|
найти
все
ситуации,
оптимальные
по
Парето в чистых стратегиях. Есть ли
в
этой игре
равновесные ситуации в чистых стратегиях?
6. Изобразить графически в координатах (K
t
, K
2
) множество всевозможных
векторов выигрышей в смешанных стратегиях в игре «семейный спор» (см. п. 1.4).
Указание. Произвольные смешанные стратегии х и у игроков 1 и 2 соответст-
венно могут быть записаны в виде х=({,
1
—£),
У=(1,
1—1)>
€>
V
e
V>>
1]- Записывая
функции
выигрыша К
г
и К
г
в смешанных стратегиях и исключая
один из
параметров,
получаем однопараметрическое семейство отрезков, объединение которых и есть
искомое множество (см. рис. 9). Криволинейная часть границы представляет собой
огибающую этого семейства отрезков и является частью параболы:
5A^+5X|_-IOA:
1
X
2
-I8(A:
1
+A:
2
)+45=O.
7.
Воиматричной игре с матрицами
А =
[
6 0 2~| Г6 0 71
0 4 3, В= 0 4 0 I
7 0 oj |_2 3 Oj
найти вполне смешанную ситуацию равновесия по Нэшу. Имеет ли эта игра еще
ситуации равновесия в смешанных стратегиях?
Указание. Найти сначала вполне смешанную ситуацию равновесия (х, у),
х=(^
и
£
2
,
£
3
)»
У "(flu f
2> "з)>
затем такую равновесную ситуацию, для которой {
t
=0,
и т. д.
8.
«Игра
на
оригинальность»
[23]. Рассматривается бескоалиционная игра л лиц
171

Г-W
{X,},
eHt
Wi,id.
где *,={0, 1}, Я,(0, .... 0|1)-Й>0, tf,(l, .... 1||0) =
А,>0,
i i
Я,(х)=0 в остальных случаях, где || означает, что замена производится на »'-м месте.
i
а) Интерпретировать игру в терминах рекламного дела.
б) Найти вполне смешанную ситуацию равновесия.
9. В п. 10.1 гл. I было показано, что игры двух лиц с нулевой суммой можно
решать методом «фиктивного разыгрывания». Рассматривая биматричную игру
с матрицами
Г2 0 1~| Г1 0 2~|
I 1 2 0 I 2 10.
1_0 1 2_| |_0 2 lj
показать, что этот метод не может быть использован для нахождения ситуаций
равновесия в биматричных играх.
10.
Игра «музыкальные стулья»
[10].
Имеются два игрока и три стула, помечен-
ные цифрами 1, 2, 3. Стратегия игрока состоит в выборе номера стула. Оба игрока
несут потери при выборе одного и того же стула. Если же их выборы различны, то
тот игрок, например /, чей стул следует фазу за стулом игрока у, выигрывает вдвое
больше, чем игрок j (предполагается, что стул 1 следует за стулом 3). Получаем
биматричную игру Г
(А,
В),
[
(0,
0) (1, 2) (2, 1)"|
(2,
1) (0, 0) (1, 2) .
(1,
2) (2, 1) (0, 0)J
а) Показать, что единственное вполне смешанное равновесие по Нашу состоит
в равновероятном выборе стульев каждым игроком.
б) Показать, что равновесие в совместных смешанных стратегиях имеет вид
fl/б,
если 1ф},
LihJ)=\
. . .
I 0, если i—j.
в) Показать, что выигрыши в ситуации равновесия по Нашу не являются оп-
тимальными по Парето, а
равновесие
в совместных смешанных стратегиях приводит
к выигрышам (
3
/
2
,
/
2
),
оптимальным по Парето.
11.
Равновесие в совместных смешанных стратегиях
не
обязывает игроков приде-
рживаться чистых стратегий, реализовавшихся в результате принятой совместной
смешанной стратегии (см. определение п. 6.1). Если же мы обязаны придерживаться
результатов конкретной реализации совместной смешанной стратегии, то можно
обобщить «равновесие в совместных смешанных стратегиях». Для всех ieN обозна-
чим через ц
(N\
{>})
сужение распределения ц на множество Х^
{,•}
= ]~[
Xj,
а именно
16МЙ
для всех xeY[
Xi-
Будем говорить, что ц есть слабое равновесие в совместных
ieN
смешанных стратегиях, если выполнены следующие неравенства для всех ieN
nyieXf.
172

хе
а) Доказать, что всякое равновесие в совместных смешанных стратегиях являет-
ся слабым равновесием в совместных смешанных стратегиях.
б) Пусть //=(/*,, ..., fi
n
) — векторная ситуация в смешанных стратегиях в игре Г.
Показать, что вероятностная мера Д= J~[
ц,
на множестве Х= ]~[ X, является слабым
равновесием в совместных смешанных стратегиях и равновесием в совместных
стратегиях тогда и только тогда, когда ситуация n={ji
l3
••-, pi
n
)
равновесна по Нашу.
12.
а) Доказать, что в игре, сформулированной в упр. 10, множество ситуаций
равновесия по Нэшу, множество ситуаций равновесия в совместных стратегиях
и множество ситуаций слабо равновесных в совместных смешанных стратегиях
различны и не совпадают между собой.
б) Показать, что множество вектор-выигрышей, оптимальных по Парето среди
выигрышей в ситуации равновесия в совместных смешанных стратегиях, покрывает
отрезок [(
5
/
3
,
4
/
3
), С7з,
5
/з)],
а выигрыши, оптимальные по Парето среди слабо
равновесных в совместных смешанных стратегиях, покрывают отрезок
[(2,
1),
(1,
2)].
Г 2 -1-
13.
Найти арбитражное решение биматричной игры с матрицами
А
=
Г 1 -П
5=1
I,
используя схему Наша.
14.
Рассмотрим биматричную
(2 х
2)-игру с матрицей
Pi Pi
а1
Г(1,1) (1,2) "I
«
2
L(2,
l) (-5, 0)J
Это модификация игры «перекресток» (см. пример 2 п. 1.4), отличие которой
заключается лишь в следующем. Водитель легкового автомобиля (игрок
1)
и грузо-
вого (игрок
2)
по-разному оценивают результаты аварии (ситуация (а,,
/}
2
)).
Пока-
зать,
что анализ игры в стратегиях угроз предписывает ситуацию (а,, р
2
), т. е.
грузовому автомобилю «ехать», а легковому — «остановиться».
15.
Пусть ядро имеет
непустое
пересечение
со всеми
гранями
a,=v({i})
множества
дележей. Показать, что в этом случае оно является единственным
Я—
Af-решением.
16.
Для кооперативной игры (N, ») определим полудележ как вектор a=(atj
а„),
для которого
«/>»({»})
н
Z *<<»М- Показать, что если L есть Я—М-решение
игры (N, с) и a
—
полудележ, не принадлежащий L, то существует такой дележ fieL,
что jS>r г.
17.
Для игры (N, v) определим ft равенством
ft- max KSU0'})-»(S)].
Показать, что если найдется /, для которого
a,>ft,
то дележ ос не может
принадлежать ни ядру, ни одному из Я
—
Af-решений.
18.
Пусть (N, ») — простая игра в (0 — 1)-редуцированной форме (см. п. 10.6).
Игрок i называется «вето»-игроком, если f(7V\{i'}/=0.
173

а) Доказать, что для того, чтобы С-ядро в простой игре было непустым,
необходимо и достаточно, чтобы в игре существовал хотя бы один «вето»-игрок.
б) Пусть S
—
множество всех «вето»-игроков. Показать, что дележ ot=(aj,..., a„)
принадлежит С-ядру, если £
а,-=1,
а,>0, для ieS, и
щ—0,
для i^S.
19.
В игре (N, v) под квазидележом будем понимать вектор a=(a,, ..., ац), такой,
что Y.
OLI=V(N)-
Для
каждого
«>0 определим строгое
в —
ядро
С,(ю),
как множество
квазидележей таких, что для каждой коалиции
£ «i>v(S)-e.
ieS
а) Показать, что если е<е', то С,(е)с=С,<, (»).
б) Показать, что существует наименьшее число, для которого C,(t>)#0. При
таком
Е
множество С,(«) называется минимальным е-ядром и обозначается через
MC(v).
в) Найти минимальное «-ядро в игре
(N,
«), где N={1, 2, 3);
•>({'})=<>> »({1» 2})=50, ,({1, 3})=80, .({2, 3})=90, .{Л}-100.
г) Пусть (iV, v), (N,
v
1
)
— две кооперативные игры и для некоторых £ и г'
выполняется равенство
C,(c')
= C,'(i;)#0. Показать, что в этом случае для всех 5>0,
C«-i(»)=Q-«(»')- В частности, MC(v)=MC(v
r
).
20.
Показать, что если (N, v)
—
игра с постоянной суммой (см. п. 9.3), то вектор
Шелли if определяется по формуле
Г(л-*)!(*-1)! И
лМ-2 S \- ~j—~v(S) \-v(N).
21.
Игра (N, v) называется выпуклой, если для всех S, TaN
v(S\J1)+v(Sf]T)>v(S)+v(T).
а) Доказать, что выпуклая игра имеет непустое С-ядро и вектор Шелли принад-
лежит С-ядру.
б) Показать, что (N, v)
—
выпуклая игра, если
а т=(т
и
.... /и„) — неотрицательный вектор.
22.
Рассмотрим простую игру (N, v) в (0 — 1)-реАудированной форме. Под
«скачком» игрока i будем понимать такое множество
SczN,
для которого
«(5)
=
1,
а v(S \{/})=0. Обозначим через 0,- число скачков игрока i в игре. Тогда вектор
P(
v
)=(fii
(«)
Дп(")).
г
Д
е
A(«)=fy/ Z fy называется вектором Банзафа для простой
игры.
а) Для простой игры четырех лиц
(N,
«),
в которой коалиция S выигрывает, если
она состоит либо из двух игроков и игрока
{1}
eS, либо из трех игроков или четырех
игроков, показать, что
0
t
=6,
в
2
=в
3
=
В^=2н, следовательно /f(»)=(l/2,1/6,1/6,1/6).
б) Показать, что
/? (г)
совпадает в игре упр. (2.2 а) с вектором Шепли.
174

23.
Пусть
{N,
v)
— простая игра трех
лиц,
в которой коалиции
(1,
2),
(1,
3),
(1,
2, 3)
являются единственными выигрывающими коалициями. Показать, что в этой игре
0j
=
3,
в
2
=
в
3
= 1
и, следовательно, вектор Банзафа имеет вид
/((и)
=
(3/5,
1/5, 1/5),
а вектор Шегош равен <р[«]=(2/3, 1/6, 1/6).
24.
Рассмотрим неотрицательный вектор р—(л,, ..., я„) и число 0>О. Пусть
п
О<0< £
я
'-
Взвешенной игрой большинства
будем называть простую игру (N, v),
1-Ъ .
в которой характеристическая функция
v
определяется по правилу
\ 0, если £
n
i<0>
»(S)=<
ieS
( 1, если Y,
Щ>0-
ieS
Пусть0=8ир=(4, 3, 3,2, 2,1), л=6. Вычислить вектор
Шепли
и вектор Банзафа
для простой взвешенной
игры
большинства.

ГЛАВА IV
ПОЗИЦИОННЫЕ ИГРЫ
§
1.
МНОГОШАГОВЫЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
1.1. В предыдущих главах нами рассматривалась игра в нор-
мальной форме. К такой форме в принципе может быть сведен
динамический (т. е. протекающий в течение некоторого времени,
а не мгновенно) конфликтно-управляемый процесс формальным
введением понятия чистой стратегии. В тех немногочисленных слу-
чаях, когда мощность пространства стратегий невелика и имеется
возможность численного нахождения решений, такой подход явля-
ется вполне допустимым. Однако в большинстве задач поиска
оптимального поведения участников конфликтно-управляемого
процесса переход к нормальной форме, т. е. сведение задачи к одно-
кратному выбору чистых стратегий как элементов пространств
больших размерностей или функциональных пространств, не приво-
дит к эффективным способам нахождения решений, хотя и позволя-
ет наглядно иллюстрировать те или иные принципы оптималь-
ности. В ряде случаев общие теоремы существования решения для
игр в нормальной форме не позволяют находить или даже конк-
ретизировать оптимальное поведение в играх, нормализацией кото-
рых они являются. Как будет показано ниже, в «шахматах» суще-
ствует решение в классе чистых стратегий. Однако этот результат
невозможно получить прямым исследованием матричной игры.
Еще более отчетливо это обстоятельство проявляется при исследо-
вании дифференциальных игр преследования, для которых в ряде
случаев удается находить решения в явной форме, однако нормаль-
ная форма дифференциальной игры является настолько общей, что
получение конкретных результатов оказывается практически невоз-
можным.
1.2. Математические модели конфликтов, учитывающие динами-
ку, исследуются в теории
позиционных
игр.
Наиболее простым клас-
сом позиционных игр является класс
конечношаговых
игр с
полной
информацией.
Для определения конечношаговой игры п лиц с пол-
ной информацией потребуются элементарные сведения из теории
графов.
Пусть X
—
некоторое конечное множество. Правило/, ставящее
в соответствие каждому элементу х е X элемент Дх)еХ, называется
однозначным отображением X в X или функцией, определенной на
176

X
и
принимающей значения в X. Многозначное отображение F мно-
жества
X в
X — это правило, которое каждому элементу
хеХ
ставит в соответствие некоторое подмножество F
x
aX (при этом не
исключается возможность
F
x
=0).
В
дальнейшем для простоты
будем употреблять термин «отображение», понимая под ним «мно-
гозначное отображение».
Пусть F
—
отображение X
в
X, а А с X. Под образом множества
А будем понимать множество
FA={jF
x
.
хеЛ
По определению полагаем F(0)=0. Можно убедиться
в
том,
что если
A
t
<=-X,
i=
1,
..., п, то
*{и
А=U
FA
»
*{п
^)<=
П
FA,
\;-1
/ i-i V-i / i-i
Определим отображения F
2
, F
3
, ...,
F,
..., следующим образом:
/«=№),
F?=F(F?), ..., F
k
x
=F{F
k
-\ ...
(1.1)
Отображение F множества X
в
X называется
транзитивным
замыка-
нием отображения F, если
A-MlteUtfU-UtfU-"
0-2)
Отображение
JF*
-1
,
обратное отображению F, определяется как
F;
l
=
{x\yeF
x
},
т. е. это множество тех точек х, образ которых содержит точку
у.
Аналогично отображению F
x
определяется отображение
(F~
1
)*,
т. е.
(F-^-F-'iiF-
1
),),
(1.3)
Если -ВсЛТ, то полагаем
,Г
1
(5) =
{х|^П^^0}-
(1-4)
Пример 1.
(Шахматы.)
Каждая позиция на доске определяется
как количеством
и
составом фигур каждого игрока, так
и
их рас-
положением
в
данный момент
и
указанием того, кто из игроков
должен в этот момент играть. Пусть заданы: X
—
множество пози-
ций, F„
хеХ
— множество тех позиций, которые могут реализо-
ваться непосредственно после позиции
х.
Если
в
позиции
х
число
белых и черных фигур равно нулю, то F
x
=0. Тогда F
x
, определя-
177

емое (1.1), есть множество позиций, которое может быть получено
из х за к ходов; F
x
— множество всех позиций, которые могут быть
получены из х; F~
l
(A) (AczX) — множество тех позиций, из кото-
рых за один ход возможен переход в позиции из множества А (см.
(1.2) и (1.4)).
Изображая позиции точками и соединяя стрелкой две позиции
х и у,
yeF
x
,
теоретически можно построить граф игры, исходящий
из начальной позиции. Однако из-за очень большого числа позиций
нарисовать такой граф невозможно.
Использование многозначных отображений над конечными мно-
жествами позволяет представить структуру многих многошаговых
игр:
шахмат, шашек, игры «го» и др.
Определение. Пара (X, F)
называется
графом,
если
X—
неко-
торое конечное
множество,
a F
— отображение
X в X.
Граф (X, F) будем обозначать символом G. В дальнейшем
элементы множества X будем изображать точками на плоскости,
а пары точек х и у, для которых yeF„ соединять непрерывной
линией со стрелкой, направленной от х к у. Тогда каждый элемент
множества X называется вершиной или узлом графа, а пара элемен-
тов (х, у), в которой
yeF
x
— дугой графа. Для дуги р
=
(х,
у)
вершины х я у называются граничными вершинами дуги, причем
х — начало, а у — конец дуги. Две дуги р и q называются смеж-
ными, если они различны и имеют общую граничную точку.
Множество дуг в графе будем обозначать Р. Задание множества
дуг в графе G=(X, F) определяет отображение F и, наоборот,
отображение F определяет множество Р. Поэтому граф G можно
записывать как в виде G=(X, F), так и в виде G=(X, Р).
Путем в графе
G—(X,F)
называется такая последовательность
Р=(Ри
Рг>
•••> Рь •••) ДУГ, что конец каждой предыдущей дуги
совпадает с началом следующей. Длина пути р=(р
1г
...,
Рк)
есть
число 1(р)=к дуг последовательности; в случае бесконечного пути
р полагаем
1(р)=
со.
Ребром графа G=(X, P) называется множество из двух элемен-
тов х, уеХ, для которых или (х, у)еР, или (у, х)еР. В отличие от
дуги для ребра ориентация роли не играет. Ребра будем обозначать
буквами р, q, а множество ребер — Р. Под цепью будем понимать
последовательность ребер (p
v
p
2
, ...), в которой у каждого ребра
р
к
одна из граничных вершин является также граничной для Рк-\,
а другая — граничной для
p
k+
i.
Цикл — это конечная цепь, начинающаяся в некоторой вершине
и оканчивающаяся в той же вершине. Граф называется связным,
если любые две его вершины можно соединить цепью.
Дерево или древовидный граф, по определению, есть конечный
178
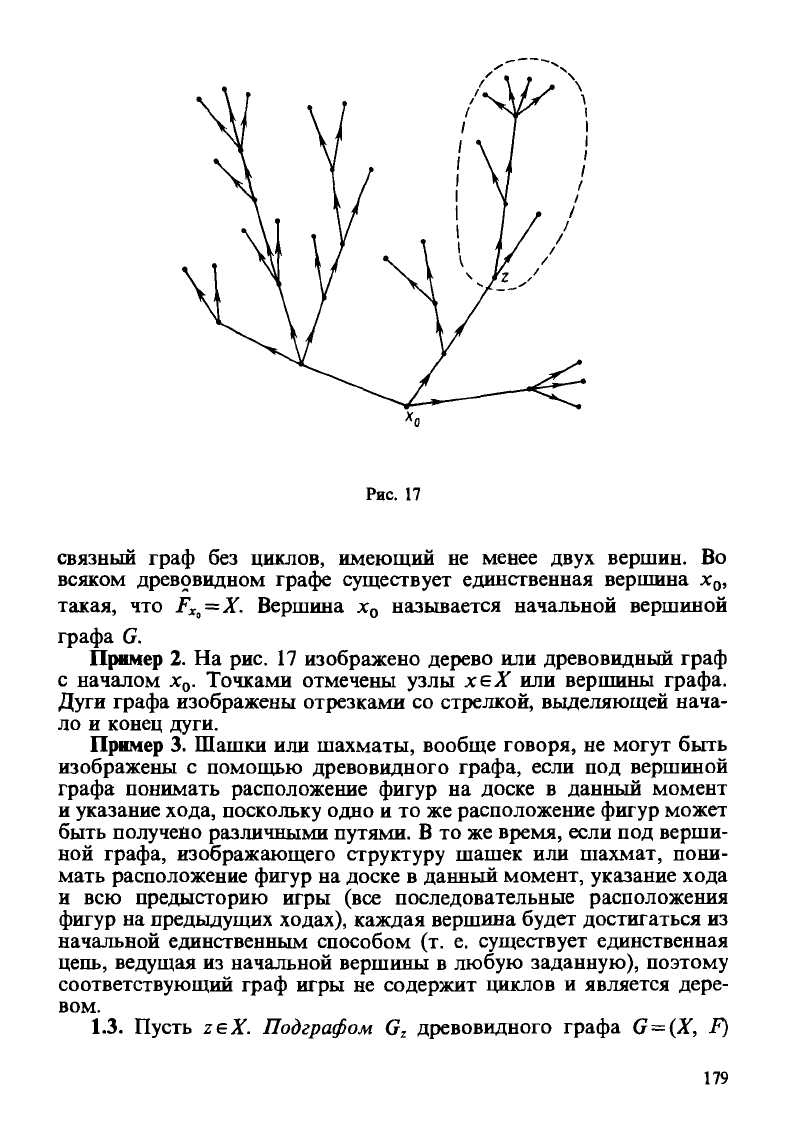
Рис.
17
связный граф без циклов, имеющий не менее двух вершин. Во
всяком древовидном графе существует единственная вершина х
0
,
такая, что
F
Xa
= X. Вершина х
0
называется начальной вершиной
графа G.
Пример 2. На рис. 17 изображено дерево или древовидный граф
с началом х
0
. Точками отмечены узлы хеХ или вершины графа.
Дуги графа изображены отрезками со стрелкой, выделяющей нача-
ло и конец дуги.
Пример 3. Шашки или шахматы, вообще говоря, не могут быть
изображены с помощью древовидного графа, если под вершиной
графа понимать расположение фигур на доске в данный момент
и указание хода, поскольку одно и то же расположение фигур может
быть получено различными путями. В то же время, если под верши-
ной графа, изображающего структуру шашек или шахмат, пони-
мать расположение фигур на доске в данный момент, указание хода
и всю предысторию игры (все последовательные расположения
фигур на предыдущих ходах), каждая вершина будет достигаться из
начальной единственным способом (т. е. существует единственная
цепь,
ведущая из начальной вершины в любую заданную), поэтому
соответствующий граф игры не содержит циклов и является дере-
вом.
1.3. Пусть zeX. Подграфом G
z
древовидного графа G
=
(X,
F)
179
