Петросян Л.А. и др. Теория игр

Подождите немного. Документ загружается.

называется граф вида (X

, F

где

x=F

(^\X

На

рис.

штриховой линией обведем подграф, берущий начало из вершины z.

В древовидном графе для всех

xeX

множество

совпадают,

т. е.

отображение

является сужением отображения

на

множество

Поэтому

для

подграфов древовидного графа

будем использовать обозначение

=(X

F).

1.4. Перейдем теперь

определению

многошаговой игры

полной

информацией

на

древовидном конечном

графе.

Пусть

G=(X,

F) — древовидный граф. Рассмотрим разбиение

я+1

множества вершин

па.

п+l

множество

, ..., Х

X„

=X,

(\X,=

0, кф1, где

для

хеХ„

Множество

X„ /=1, ...,

п называется

множеством очередности

1-го

игрока,

множество

—множеством

окончательных

позиций.

На

множестве окон-

чательных позиций Х„

1 определены

вещественных функций

(x),

...,

(х),

хеХ

я+1

Функция #

(

(х),

/=1, ..., л,

называется

выигрышем

i-ro

игрока.

Игра происходит следующим образом. Задано множество

иг-

роков, перенумерованных натуральными числами

1, ..., i, ..., п (в

дальнейшем iV={l,

2, ...,

п}). Пусть x

eA"

ilS

тогда

вершине (пози-

ции)

<аодит» игрок

выбирает вершину

Xj^eF^.

Если

ХуеХ^,

то

вершине

х,

«ходит» игрок

выбирает следующую вершину

(позицию) x

т.

д.

Таким образом, если на k-м шаге вершина

(позиция)

дг*_1

еХь,

то

ней «ходит» игрок /*и выбирает следующую

вершину (позицию)

из

множества

Игра прекращается,

как

только достигается окончательная вершина (позиция)

xieX„

т. е.

такая, для которой

В результате последовательного выбора позиций однозначно

реализуется некоторая последовательность

, ..., х

...,

опреде-

ляющая путь

древовидном графе

исходящий

из

начальной

позиции

достигающий одной

из

окончательных позиций игры.

Такой путь

дальнейшем будем называть

партией.

Из-за древовид-

ности графа

каждая партия однозначно определяет окончатель-

ную позицию

Xi,

которую она приводит,

и,

наоборот, окончатель-

ная позиция

однозначно определяет партию.

позиции

х,

каждый

из игроков

I, i=l, ...,

п, получает выигрыш

(

(х1).

Будем предполагать, что игрок

при совершении выбора

пози-

180

ции xeXj знает эту позицию х, а следовательно, из-за древовид-

ности графа G может восстановить и все предыдущие позиции.

В таком случае говорят, что игроки имеют полную информацию.

Примером игр с полной информацией служат шахматы и шашки,

поскольку в них игроки могут записывать ходы, и поэтому можно

считать, что они знают предысторию игры при совершении каждого

очередного хода.

Определение.

Однозначное отображение

и,, которое каждой

вершине (позиции)

хеХ,

ставит

соответствие некоторую вершину

(позицию)

yeF

называется стратегией игрока

Множество всевозможных стратегий игрока i будем обозначать

через U,.

Таким образом, стратегия i'-го игрока предписывает ему в любой

позиции х из множества его очередности X, однозначный выбор

следующей позиции.

Упорядоченный набор и=(и

, ...,

и„

..., и,), где м

(

е U

называется

ситуацией

в игре, а декартово произведение

U= Y[

—

множе-

ством

ситуаций.

Каждая ситуация

(и

..., и,-, ..., и„) однозначно

определяет партию в игре, а следовательно, и выигрыши игроков.

Действительно, пусть

Тогда в ситуации и=(и

...,

и„

...,

и„)

следующая позиция х

определяется однозначно по правилу

)=x

. Пусть теперь

х^еХ^.

Тогда х

определяется однозначно

по правилу и,

(х

)=х

. Если теперь на fc-м шаге реализовалась

позиция х*_1бАГ^ то х

определяется однозначно по правилу

**=«*(**-0.

ит

Пусть ситуации u=(u

...,

и„

...,

ы„)

в указанном смысле соответ-

ствует партия х

, х

..., х/. Тогда можно ввести понятие функции

выигрыша

К, игрока i, положив ее значение в каждой ситуации

и равным значению выигрыша Я, в окончательной позиции партии

,...,

соответствующей ситуации м=(и

, ..., ы„), т. е.

K,(u

..., и , ы

)=Я,(х,), i=l, ..., п.

Функции

i= 1,..., п, определены на множестве ситуаций

U= Y[

Таким образом, построив множества стратегий игроков

и опре-

делив на декартовом произведении функции выигрыша

К„

/=1, ...,

181

я,

получаем некоторую игру в нормальной форме

T=(N,

{и,},

вК

{K,}

ieN

где iV={l, ..., i, ..., п) — множество игроков,

С/,

— множество стра-

тегий игрока I,

— функция выигрыша игрока /, /=

.., п.

1.5. Для дальнейшего исследования игры Г необходимо ввести

в рассмотрение понятие

подыгры,

т. е. игры на подграфе графа

G основной игры (ср. с. п. 1.1 гл. I).

Пусть zeX. Рассмотрим подграф G

F), с которым свяжем

подыгру Г

следующим образом. Множества очередности игроков

в подыгре Г

определяются по правилу

Yj=Xif)X

i=\, ..., п,

множество окончательных позиций

„

if]X

выигрыш игро-

ка

Щ(х) в подыгре полагается равным

H\(x) = H

{x),xsYUx,i=\,...,n.

В соответствии с этим стратегия и] i-ro игрока в подыгре Г

опреде-

лена как сужение стратегии u, i-ro игрока в игре Г на множество Y],

т. е.

и]{х) =

щ{х),

хе У?=ЛГ,П*« i=l, .... п.

Множество всех стратегий г-го игрока в подыгре обозначается через

Щ. В результате с каждым подграфом G

мы связываем подыгру

в нормальной форме

Г,=(АГ,

{с/?},

т\.

где функции выигрыша Щ, /=1, ..., п, определены на декартовом

произведении (/=\\ Щ.

i-l

§ 2. СИТУАЦИЯ АБСОЛЮТНОГО РАВНОВЕСИЯ

В гл. III было введено понятие равновесия по Нашу для игры

п лиц в нормальной форме. Оказывается, что для многошаговых

игр можно усилить понятие равновесия, введя понятие абсолютного

равновесия.

2.1.

Определевие.

Ситуация равновесия по

Нэшу

(uf,...,

uf)

называется ситуацией абсолютного равновесия

по Нэшу в игре Г,

если для любого zeX

ситуация

(ы*У =

((«*/,

...,

(u*)

где (uf)

—

сужение стратегии

uf на

подыгру

, является

ситуацией

равнове-

сия по Нэшу в

подыгре

182

Имеет место следующая основная теорема.

Теорема. В любой

многошаговой

игре с

полной информацией

на

конечном

древовидном

графе существует ситуация абсолютного

равновесия

по Нэшу.

Прежде чем перейти к ее доказательству, введем понятие длины

игры. Под длиной игры Г будем понимать длину наибольшего пути

в графе G=(X, F).

Доказательство проведем индукцией по длине игры. Если

длина игры Г равна 1, то может ходить лишь один из игроков,

который, выбирая следующую вершину из условия максимизации

своего выигрыша, будет действовать согласно стратегии, образу-

ющей абсолютное равновесие по Нэшу.

Пусть теперь игра Г имеет длину к и

(т. е. в начальной

позиции х

ходит игрок i\). Рассмотрим семейство подыгр Г„

zeF

длина каждой из которых не превосходит

к— 1.

Предположим, что

теорема справедлива для всех игр, длина которых не превосходит

А:— 1,

и докажем ее для игры длины к. Поскольку подыгры Г„

zeF

Xti

имеют длину не более к—\, по предположению индукции для них

теорема справедлива и тем самым существует ситуация абсолют-

ного равновесия по Нэшу. Обозначим для каждой подыгры Г

zeF

X(t

эту ситуацию через

(ц*)'=ыУ,...,

(и*П

(2.1)

Используя ситуации абсолютного равновесия в подыграх Г

построим ситуацию абсолютного равновесия в игре Г. Пусть

uf(x)

(uf(x))

, для

xeXif)X

zeF^, i=l, ..., п, uf

)=z*, где z*

находится из условия

*СК"*)1=

тах

*и("*Л-

(2-2)

ер

Функция uf определена на множестве X

i= l, ..., л, очередности

1-го игрока, а при каждом фиксированном

xeX

значение

uf(x)eF

Таким образом, uf, i= 1,..., и, является стратегией z'-ro игрока в игре

Г, т. е. ufeUt. По построению, сужение (м,*)

стратегии uf на

множество

f\X

является стратегией, входящей в абсолютное

равновесие по Нэшу игры Г„

zeF

x<>

Следовательно, для завершения

доказательства теоремы достаточно показать, что стратегии uf,

/=1,

..., и, построенные по формулам (2.2), образуют ситуацию

равновесия по Нэшу в игре Г. Пусть i^i

По построению стратегии

183

и* после выбора игроком i

позиции z* на первом шаге игра

Г переходит в подыгру T

.. Поэтому

К,

(и*) = К? {(u*f) >

Щ'

{(и*

|| uf) =

К,

(и*

||i0,

u,eU„i=l, ...,п,1ф^, (2.3)

так как (и*) — ситуация абсолютного равновесия в подыгре Г

Пусть и

е U

— произвольная стратегия игрока i

в игре Г. Обозна-

чим z

). Тогда

(и*)=К*

{(и*)

=max K\

{(u*)

)

Ж*;

{(u*)

°}>K%

{(и*|кЛ

=К

(и*\\и

(2.4)

Утверждение теоремы следует теперь из (2.3), (2.4).

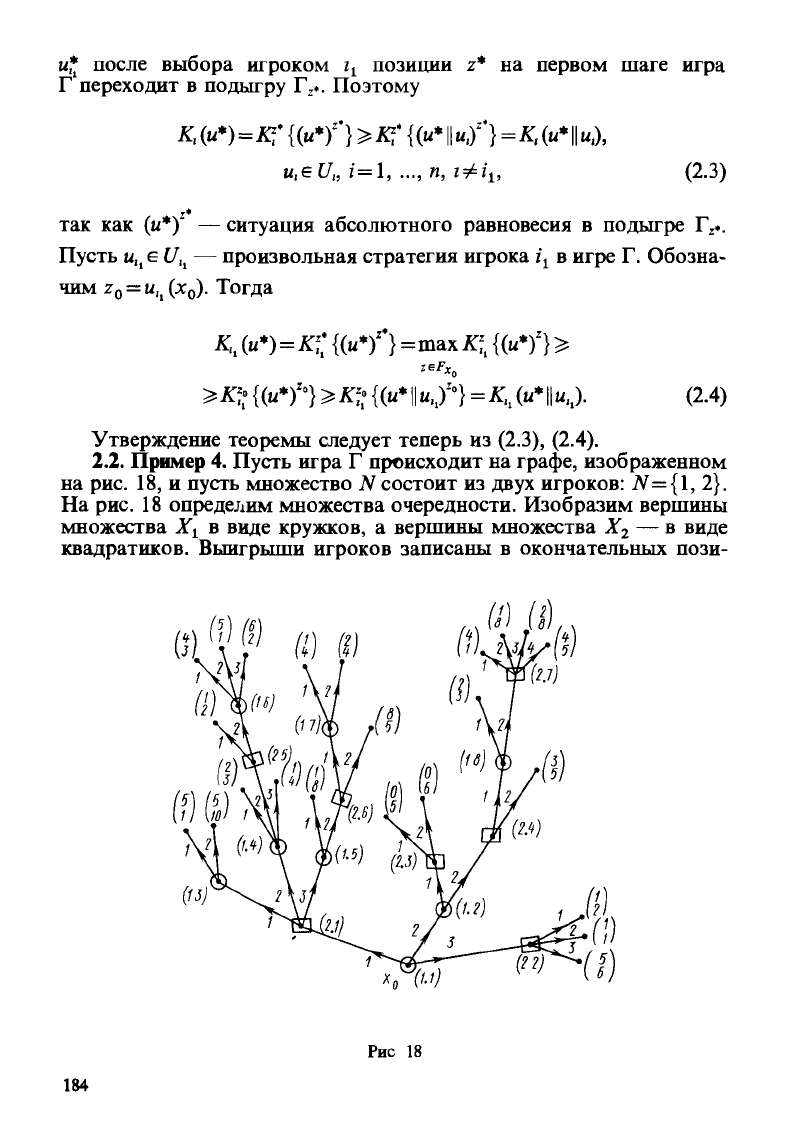
2.2.

Пример 4. Пусть игра Г происходит на графе, изображенном

на рис. 18, и пусть множество N состоит из двух игроков:

JV={1,

2}.

На

рис.

18 определим множества очередности. Изобразим вершины

множества Х

в виде кружков, а вершины множества Х

— в виде

квадратиков. Выигрыши игроков записаны в окончательных пози-

Рис 18

184

циях. Перенумеруем двойными индексами позиции, входящие

в множества X

и Х

, а дуги, выходящие из каждой вершины,—

одним индексом. Выбор в вершине х эквивалентен выбору следу-

ющей вершины х"eF

, поэтому будем предполагать, что стратегии

указывают в каждой вершине номер дуги, по которой следует

двигаться дальше. Например, стратегия

«!

(2,

1, 2, 3, 1, 2, 1, 1)

игрока 1 предписывает ему выбор дуги 2 в вершине 1, дуги 1 — в

вершине 2, дуги 2 — в вершине 3, дуги 3 — в вершине 4 и т. д. Так

как множество очередности первого игрока состоит из восьми

вершин, то его стратегия представляет собой восьмимерный вектор.

Аналогично, любая стратегия игрока 2 представляет собой семи-

мерный вектор. Всего у первого игрока 864 стратегии, а у второго

игрока — 576 стратегий. Таким образом, соответствующая нор-

мальная форма оказывается биматричной игрой с матрицами раз-

мера 864x576. Естественно, что решение таких биматричных игр

методами, предложенными в гл. III, не только затруднительно, но

и невозможно. Вместе с тем рассматриваемая игра достаточно

проста и ее можно решить, используя попятную процедуру постро-

ения абсолютного равновесия по Нэшу, предложенную при до-

казательстве теоремы 1 п. 2.1.

Действительно, обозначим через

(x),

(х)

выигрыши в подыг-

ре Г

в некоторой фиксированной ситуации абсолютного равнове-

сия.

Сначала решаем подыгры Г

, Г17, Г

л- Как легко убедиться,

*.(1.7) =

(1.6)=2, M1.7)=2, »

(1.7)=4,

(2.7) = l, «

(2.7) = 8.

Далее решаем подыгры Г

, Г

Г]

В подыгре Г

два равновесия

по Нэшу, поскольку игроку 2 безразлично, какую альтернативу

выбрать. Вместе с тем его выбор оказывается существенным для

игрока

поскольку при выборе игроком 2 левой дуги первый игрок

выигрывает +1, а при выборе игроком 2 второй дуги +6. Отметим

это обстоятельство и предположим, что игрок 2 «благожелателен»

и выбирает в позиции (2.5) правую дугу. Тогда «

(2.5)=«

(1.6) =

(2.5)=v

(1.6)=2, v

(2.6)=v

(l.1)=2, «

(2.6)=t>

(1.7)=4,

(1.8) =

Далее решаем игры Г13, Г

, Г

, Г^, Г

В подыгре

Tj 3

два равновесия по Нэшу, поскольку игроку 1 безраз-

лично, какую альтернативу выбрать. Вместе с тем его выбор оказы-

вается существенным для игрока 2, так как при выборе игроком

1 левой альтернативы он выигрывает 1, а при выборе правой — 10.

Предположим, что игрок

«благожелателен» и выбирает в позиции

(1.3) правую альтернативу. Тогда «

(1.3) =

(1.3)

=10,

(1.4) = «

(2.5) = 6, „

(1.4)=г,

(2.5)=2, ^(1.5)=„,(2.6) =

(1.5) = «

(2.6)=4,

в1

(2.3) = 0, *

(2.3) = 6,

(2.4) =

*,(2.^=5. Да-

лее решаем игры Г

2Ь

, Г

^: v

(2.1)=v

(\.3)

•

(2.1) = «

(1.3) =

10,

(1.2)=«

(2.4) =

(1.2)=»

(2.4) =

185

(2.2)=—5,

(2.2) =

Теперь решаем игру Г=Г

1Л

. Здесь

(l.l)

= »

(2.1) = 5,e

(l.l)=i»

(2.1)=10.

В результате мы получаем ситуацию абсолютного равновесия по

Нэшу (и?, м?), где

= (1,2,2,2,2,3,2,1),

н!

(1,3,2,2,2,1,2).

(2.5)

В ситуации (uf, uf) игра развивается по пути (1.1), (2.1), (1.3).

В процессе построения было замечено, что стратегии uf, i=l, 2,

«доброжелательны» в том смысле, что игрок i при совершении

своего хода, будучи в равной степени заинтересован в выборе

последующих альтернатив, выбирает ту из них, которая более

благоприятна для игрока 3 — i.

В игре Г существуют ситуации абсолютного равновесия, в кото-

рых выигрыши игроков будут другими. Для построения таких

равновесий достаточно снять условие «доброжелательности» иг-

роков и заменить его обратным условием «недоброжелательности».

Обозначим через v

(x),

(х)

выигрыши игроков в подыгре Г

при

использовании игроками «недоброжелательного» равновесия. Тог-

да имеем: «, (1.6)=«,(1.6)=6, «,(1.6)=«,(1.6)=2,

«i(l-7) = ix(1.7)=2, „

(1.7)=t,

(1.7)=4, «

(5.7)=-2,

(2.7)=«

(2.7) = 8. Как уже отмечалось, в подыгре

два равнове-

сия по Нэшу. В отличие от предыдущего случая предположим, что

игрок 2 «недоброжелателен» и выбирает ту из вершин, в которой

при его максимальном выигрыше выигрыш игрока 1 минимален.

Тогда

(2.5)

\, «2_(2.5)=2, «

(2.6)=«

(1.7)=2, «

(2.6)=i;

(1.7)=4,

(1.8)=«

(1.8)=2,

(1.8)=«

(1.8) =

Далее ищем решение игр

Г1.3,

Гц,

IYJ, Г

.з, Г2.4. В подыгре Ги два равновесия по Нэшу. Как

и в предыдущем случае, выберем «недоброжелательные»^ действия

игрока 1. Тогда имеем: «, (1.3)=v, (1.3) =

(1.3) =

»,(1.4) =

(1.4) =

(1.5)=«

(2.6)=

(l.5)=2, „

(1.5)=i;2(2.6)=

(2.6)=4,

£l

(2.3)=i;

(2.3)=0,

(2.3)=«

(2.3) = 6, v. (2.4)=

(2.4) =

(2.4)=«

(2.4)

Далее решаем игры Г

.ь Г

, Г

. Имеем:

Hi(2.1) = i

(1.5)=2, *

(2.1)=«

(1.5)_=4, «

(1.2)=»

(2.4) =

(1.2) = v

(2.4) =

(2.2)

=_«

(2.2) = 6,

(2.2) =

(2.2) =_-

Теперь

решаем игру Г=Г

. Здесь «

(1.1)=»

(1.2) =

(l.l)=«

(1.2)=5.

Таким образом, получена новая ситуация равновесия по Нэшу

Й?С) = (2,2,1,1,2,3,2,1), ы?()=(3,3,2,2,1,1,3). (2.6)

Выигрыши обоих игроков в ситуации (2.6) меньше таковых в ситу-

ации (2.5). Ситуация (2.6), так же как и ситуация (2.5), является

ситуацией абсолютного равновесия.

2.3.

Очевидно, что кроме «доброжелательных» и «недоброжела-

тельных» ситуаций абсолютного равновесия по Нэшу существует

186

целое семейство промежуточных ситуаций абсолютного равнове-

сия.

Интересным является вопрос

о том,

когда можно утверждать

отсутствие двух различных ситуаций абсолютного равновесия,

от-

личающихся выигрышами игроков.

Теорема. Пусть

выигрыши

игроков

Н,(х),

i=l, ..., п, в

игре

Г таковы,

что

если существует такое

такие

х, у, что

Я,

(х)=H

(y),

то Hi(x)

H,(y)

для

всех

ieN.

Тогда

игре

выигры-

ши

игроков

во всех

ситуациях абсолютного равновесия

совпадают.

Доказательство. Рассмотрим семейство подыгр

Г*

игры

доказательство проведем индукцией

по их

длине

1(х).

Пусть

1(х)=

и в

единственной нетерминальной позиции

ходит игрок

Тогда

ситуации равновесия

он

осуществляет выбор

из

условия

(Зс)=max

(У).

Если точка

единственная,

то

единствен

вектор выигрышей

в ситуации равновесия, равный

данном случае

Н(х)

{Н

(х),

...,

Я„(3с)}.

Если существует такая точка

хфх, что

Я,

(Зс)=Я,

(х),

то

имеется

еще

одна ситуация равновесия

выигрышами

Н(х)

{Н

(х),

...,

{5с),

...,

Н„(х)}. Однако

из

условия теоремы

следует,

что

если H,

{x)=H

(x),

то

Я,(Зс)=Я;(Зс)

для

всех

ieN.

Пусть v(x)

= {vi(x)}

—

вектор выигрышей

ситуациях равнове-

сия

одношаговой подыгре

который,

как

уже показано, опреде-

ляется единственным образом. Покажем, что если для некоторого

выполнено равенство v

i(i

)=v

(x"),

(х!, х"

таковы,

что

длины

подыгр

Гу, Г*.

равны единице),

то

(x')=v

(x")

для

всех

ieN.

Действительно, пусть

x'eX

, х"еХ^,

тогда

(x?)=H

)=max

(у),

(x")=H

(x')=m

(y)

yeFx-

(x')

Hi(x'),

(x")=H

(x")

для

всех

ieN. Из

равенства

(x')=v

(x") следует,

что

Я,

(Зс') =

(х")-

Но

тогда

по

условию

теоремы Н,(х

) = Н

(х")

для

всех

ieN.

Отсюда

(x")

)

для

всех

ieN.

Предположим теперь,

что во

всех подыграл

длиной

/(*)<£—

вектор выигрышей

ситуациях равновесия определяется

187

единственным образом и если для каких-нибудь двух подыгр Г

IV с длиной, не превосходящей к=\,

(x')=v

ii>

(x")

для некоторого

, то

Vi(x')=Vi(x")

для всех ieN.

Пусть игра Г

Хо

имеет длину к и в начальной позиции х

ходит

игрок i\. По предположению индукции для всех

zeF

в игре Г

вы-

игрыши в ситуациях равновесия по Нэшу определяются единствен-

ным образом. Пусть вектор выигрышей в ситуациях равновесия по

Нэшу в игре Г

равен {«;(z)J. Тогда, как это следует из (2.2), игрок i

в вершине х

выбирает следующую вершину

zeF

из условия

(z)=max «^(z). (2.8)

Если точка z, определяемая (2.8), единственна, то вектор с ком-

понентами Vi(x

)=Vi(z)

i=l, ..., и, и является единственным век-

тором выигрышей в ситуациях равновесия по Нэшу в игре 1\. Если

же существуют две вершины z, z, для которых v

(z)=v

(z), то по

предположению индукции, поскольку длины подыгр Г; и Г

не

превосходят

к—

из равенства v

(z)=v

(z), следует равенство

Vi(z)=Vi(z)

для всех ieN. Таким образом, и в этом случае выигрыши

в ситуациях равновесия v

), ieN, определяются единственным

образом.

§ 3. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ

3.1.

Рассмотрим

многошаговые антагонистические игры

полной

информацией.

Если в условиях п. 1.4 множество игроков состоит из

двух элементов N={1, 2} и Н

(х) = —Н^{х) для всех

хеХ

(Х

—

множество окончательных позиций в игре Г), то

г=<#,

и„кь

оказывается антагонистической многошаговой игрой с полной ин-

формацией. Очевидно, что этим же свойством обладают и все

подыгры Г

-игры Г.

Так как из условия Н

(х)=—Н

(х) немедленно следует, что

)=—

(и,,

)

для

(

всех

то в ситуации

равновесия по Нэшу (и*, и'

) выполняются неравенства

^i(«к "2X^1 ("I, "гХ-^!(«!, и

) для всех

«ieU

Пару (

и'

)

в этом случае будем называть ситуацией

равновесия

или

седловой

188

точкой,

стратегии, образующие ситуацию равновесия, оптималь-

ными.

Значение функции выигрыша

ситуации равновесия обозна-

чим буквой v

назовем значением игры

Г.

3.2.

Из

теоремы

п. 2.1

следует,

что в

антагонистической много-

шаговой игре

полной информацией

на

конечном древовидном

графе существует ситуация абсолютного равновесия,

т. е.

такая

ситуация

(и\, и\),

сужение которой

на

любую подыгру

игры

Г образует

в Г

ситуацию равновесия. Для любой подыгры

Г,

мож-

но также определить число v{y), представляющее значение функции

выигрыша

ситуации равновесия этой подыгры

называемое

значением подыгры

Как

было показано

в п. 3.2 гл. I,

значение

антагонистической игры

(т. е.

значение функции выигрыша игрока

ситуации равновесия) определяется единственным образом,

поэтому функция

v(y)

определена

для

всех уеХ±,

уеХ

является

однозначной функцией.

3.3.

Выведем функциональные уравнения

для

вычисления функ-

ции v(y).

Из

определения

v(y)

следует,

что

ь(у)=Щ((и\У,

(ulf)=

-К\

((«У,

(иЩ

где

((u\f,

(и

У)

— ситуация равновесия

подыгре

являющаяся

сужением ситуации абсолютного равновесия (и\,

MJ).

Пусть

,yeX

zeFy. Тогда,

как

это следует

из

(2.2),

имеем

v(y)=max

K\ ((«tf,

(utf)=

-max

v(z).

(3.1)

zeFy zeFy

Для

yeX

аналогично получаем

v(y)=

-K\

((«У, («У)=

-max K\

((u\f,

(м^=

zeFy

= —max (—w(z))=min v(z).

(3.2)

zeFy zeFy

Из (3.1)

(3.2) окончательно имеем

v(y)=maxi;(z),>'eAr

;

(3.3)

zeFy

v(y)=mmv(z),yeX

(3.4)

zeF

Уравнения (3.3), (3.4) решаются при граничном условии

*(y)Ux,=^

C).

(3.5)

Система уравнений (3.3), (3.4)

граничным условием (3.5) позво-

189