Пеллинен Л.П. Высшая геодезия (Теоретическая геодезия)

Подождите немного. Документ загружается.

и продифференцировав, найдем уравнение погрешностей для

гравиметрических данных

п п _

Л»оо+2

{dC

y(п-1)[Р

(sinВ)cosmL]

П=2

tn=>0

(п~ 1) [Р

пт

(sinВ) sin

rhL]i)

- l

= u

(IX.22)

где l

=*= AgJ

на6л

— Ag\v

Agio

— среднее ^значение аномалии

Фая, соответствующее начальной системе С

тп

и S'

Уравнение (IX.22) записано в нормированном виде. Нормаль-

ную систему уравнений, соответствующую уравнениям погрешно-

стей (IX.22), можно в матричном виде записать формулой вида

(V.40) в § 33, в которой вектор неизвестных Xi будет представлен

лишь поправкой

а вектор Z — поправками гармонических

коэффициентов геопотенциала С'

пт

и S'

. Аналогичным образом

могут быть разделены на две группы Хц й Z неизвестные в нор-

мальной системе уравнений, получаемой из обработки наблюде-

ний ИСЗ динамическим спутниковым методом. В группу Хц

войдут поправки негравитационных параметров — координат стан-

ций наблюдения, начальных орбитальных элементов, некоторых

параметров атмосферы, инструментальных поправок и т. д. Мето-

дом исключения полученные две системы нормальных уравнений

могут быть преобразованы к виду (V.41), а затем из связующей

системы могут быть найдены оптимальные значения параметров

Спт

И S

Такой путь, решения широко применяется при определении

гармонических коэффициентов геопотенциала. Комбинированные

выводы САО IV.3, GRIM 2 и GEM 8 приведены в табл. 16. Грави-

метрическая информация для этих выводов использовалась в виде

средних аномалий силы тяжести по трапециям 300 X 300 миль,

полученных методом коллокации (см. § 58). Помимо гравиметри-

ческой и динамической спутниковой информации, в решения

включали геометрические спутниковые данные (главным образом

результаты мировой спутниковой триангуляции, созданной с по-

мощью фотографических наблюдений спутника-баллона «Пагеос»)

и выводы по наблюдениям далеких космических летательных

аппаратов (§ 53). Благодаря привлечению гравиметрических

данных удавалось получать ряды гармонических коэффициентов

до 25-й степени, не считая отдельных коэффициентов более высо-

ких степеней.

Основная проблема в указанных комбинированных решениях

связана с установлением относительных весов разнородной кос-

мической и гравиметрической информации. Поскольку резуль-

таты оценки точности по внутренней сходимости плохо соответст-

вуют реальным погрешностям используемых данных, установле-

ние весов в значительной мере оказывается произвольной опера-

цией. Поэтому заслуживают внимания приближенные методы

совместной обработки гравиметрических и спутниковых данных,

в которых легче могут быть использованы результаты внешнего

контроля полученных выводов. В этих методах в качестве первич-

ной спутниковой информации рассматриваются найденные из

наблюдений ИСЗ значения гармонических коэффициентов геопо-

тенциала или их линейные комбинации. Большое распростране-

ние получил метод (см., например, [85, 139]), в котором к грави-

метрическим уравнениям погрешностей вида (IX.22) присоеди-

няют спутниковые уравнения погрешностей

Совместную обработку обеих групп уравнений погрешностей

ведут параметрическим методом под условием

При назначений весов выгодно использовать результаты, по-

добные представленным на рис. 63. По ним сразу находят погреш-

ности спутниковых определений коэффициентов С

пт

и S

. Исходя

из принятой точности аномалий силы тяжести, могут быть апри-

орно получены соответствующие им погрешности вывода тех же

коэффициентов по гравиметрическим данным, а затем сравнением

найденных погрешностей с определенными из внешнего контроля

получим множители, на которые следует умножить априорные

веса аномалий.

Решение может быть улучшено, если использовать дополни-

тельную статистическую информацию о порядках величин опре-

деляемых параметров. Например, имея данные о степенных дис-

персиях полученные из статистического анализа силы тяжести,

применяют метод коллокации (см. § 58, а также [130]), который

в рассматриваемом случае сводится к следующей простой вычис-

лительной операции. Достаточно к уравнениям погрешностей

(IX.23) и (IX.24) добавить уравнения вида

где последний член правой части соответствует формуле Каулы

(IX.9).

Благодаря добавлению уравнений (IX.25) улучшается

разделение неизвестных, выводы становятся более устойчивыми

и появляется возможность получения гармонических коэффи-

циентов более высоких степеней по сравнению с тем, что было бы

без использования метода коллокации.

(IX.23)

(IX.24)

(IX.25)

61.

ОПРЕДЕЛЕНИЕ ВЫСОТ КВАЗИГЕОИДА

Планетарный геоид

Как

уже

отмечалось

предыдущих разделах, результаты гар-

монического анализа возмущающего потенциала обычно исполь-

зуются

для

составления карт высот планетарного геоида

над

общеземным эллипсоидом. Хорошо известна такая карта, соста-

вленная

И. Д.

Жонголовичем

[25] на

основании выполненного

им разложения силы тяжести

по

сферическим функциям

до 8-й

степени

(см. § 57). И. Д.

Жонголович получил качественное

представление

об

основных особенностях геоида, которые после-

дующими исследованиями фигуры планетарного геоида после

появления искусственных спутников Земли были подтверждены.

После каждого нового вывода модели гравитационного поля

Земли публикуют соответствующие

им

мировые карты высот

планетарного геоида

над

общеземным эллипсоидом. Выяснилось,

что наиболее характерные особенности стабильны

как по

располо-

жению,

так и по

амплитудам.

Как

пример

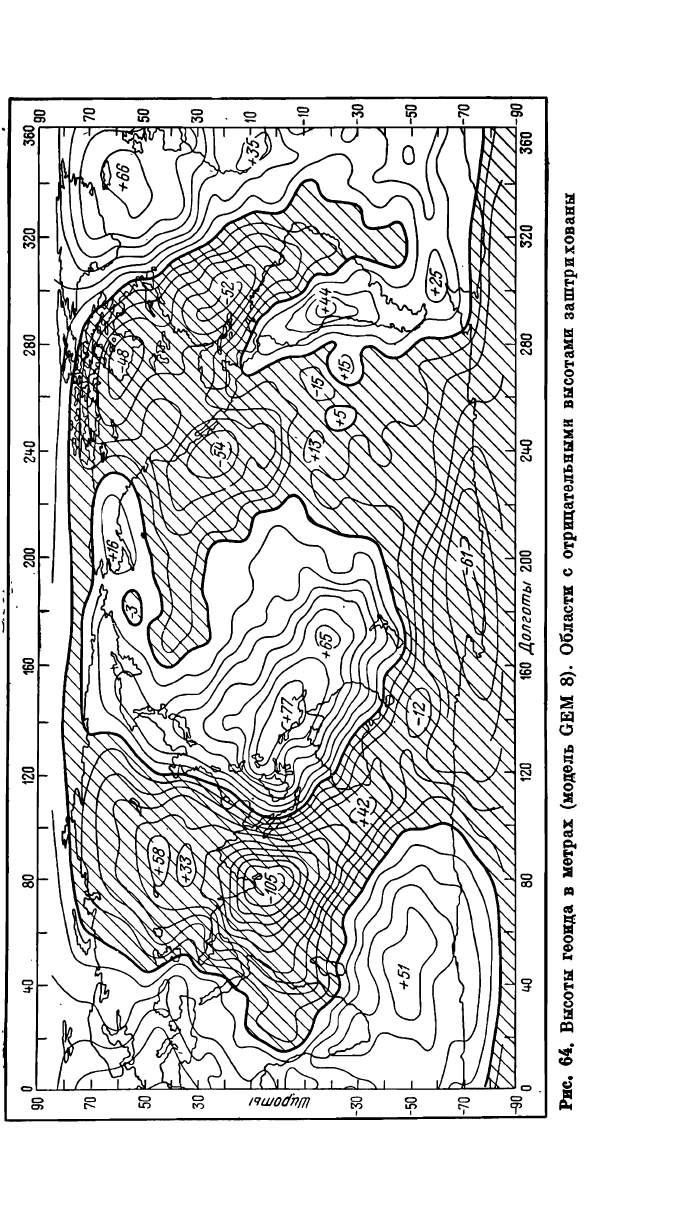
на рис. 64

приведена

карта, соответствующая комбинированной модели

GEM 8

[125].

Четко выявляются минимумы

в —105 м

вблизи южной оконечно-

сти Индостанского полуострова,

—61 м в

море Росса вблизи

Ан-

тарктиды,

—52 и —54 м в

Атлантическом

Тихом океанах вблизи

берегов Северной Америки,

—48 м в

Гудзоновом заливе,

также

максимумы

в -f- 77 м

вблизи Новой Гвинеи,

+ 66 м в

Северной

Атлантике,

+ 51 м к югу от

Африки,

-{-44 м в

Южной Америке.

Фигура геоида оказалась достаточно сложной. Трехосность

Земли (эллиптичность экватора), которую

прошлом четко

вы-

являли

по

астрономо-геодезическим

гравиметрическим данным

в основном

для

Северного полушария Земли,

не

является доми-

нирующей особенностью этой фигуры.

целом

по

Земле

не

заме-

чается корреляции высот геоида

особенностями топографии

земной поверхности. Например, высочайшая горная система Цен-

тральной Азии отражается

на

карте планетарного геоида вторич-

ным максимумом

в —33 м на

фоне крупного минимума.

Из

этого

делают вывод

о том, что

основные особенности геоида связаны

с аномалиями масс

не в

коре,

а в

более глубоких слоях Земли.

то же

время обнаружена корреляция максимумов высот геоида

с зонами повышенной сейсмической активности

на

границах

самых крупных блоков земной коры

—

литосферных плит.

Иногда обоснованно считают,

что при

геофизической интерпре-

тации фигуры планетарного геоида

за

отсчетную поверхность

надо брать уровенный эллипсоид, соответствующий гидростатиче-

скому равновесию Земли

имеющий сжатие

а — 1 : 299,67.

Чтобы перейти

высотам

над

этим эллипсоидом, следует

в их

значения

на рис. 64

ввести поправки, зависящие

от

широты

равные

—67,1 (1—1,5

соэ

Ф)

м.

Наибольшие изменения высот

будут

полярных районах,

где

выявятся значительные минимумы

высот геоида. Их иногда связывают с неполной изостатической

компенсацией полярных районов после таяния^ материковых

льдов.

Оценку точности высот планетарного геоида дадим, исходя

из формулы

(IX.6).

Имеем следующую дифференциальную зави-

симость между погрешностью высоты планетарного геоида, вы-

численного по гармоническим коэффициентам геопотенциала до

n-й степени, и погрешностями этих коэффициентов

п п _

АС;г=Д2 2 (dC

cosmL + dS

sinmL)P

(sinO)., (IX.26)

л=2

т=о

Возведем (IX.26) в квадрат и перейдем к математическим ожи-

даниям возникающих произведений. С учетом ортогональности

сферических функций в среднем по Земле будем иметь

^(?)=2С, (IX.27)

где (Q — средняя квадратическая погрешность высоты плане-

тарного геоида,

Ь&

= №

2'fag-

+4 1

(

1Х

)

— степенная дисперсия погрешностей высот планетарного геоида

тг-й степени.

Для модели GEM 7 (§ 59) имеем п = 16, т- (£) = ±2,5 м.

Точность представления найденным планетарным геоидом фи-

гуры реального квазигеоида будет ниже за счет влияния неучтен-

ных гармоник выше 16-й степени. Согласно (IX.И) оно равно

^16

(£) = ±4,0 . м. Таким образом, общая точность определения

высот квазигеоида в среднем по Земле равна

]/"(2,5)

(4,0)

4,8 м.

Аналогичным путем может быть оценена точность представле-

ния квазигеоида планетарным геоидом, вычисленным из комбина-

ции гравиметрических и спутниковых данных (§ 60). Для модели

GEM 8 (п = 25) эта точность составляет 4 м.

Использование детальных гравиметрических съемок

Развитие мировой гравиметрической съемки открывает воз-

можности для повышения точности определения высот квазигео-

ида путем сочетания вычислений по интегральной формуле Стокса

в некоторой ближайшей зоне вокруг исследуемой точки и исполь-

зования гармонических коэффициентов геопотенциала для учета

влияния дальних зон. Соответствующие формулы имеют наиболее

удобный для вычислений вид, если область а, по которой вычис-

ления ведут с помощью интегральной формулы, имеет форму

круга с центром в исследуемой точке. Имеем

2Я

^l^jj

WS (*) sinярda + ± ^ &

(

1Х

)

Л=0

2Я

4яу

j A*' [5 (яр) - 5 (©о)] sin

яр

dip da + iL ^ С» Afo.

Л=0

(IX.30)

Первая из формул получена В. Ф. Еремеевым и М. И. Юрки-

ной [69], а вторая — О. М. Остачем [81]. Через \р

обозначен

сферический радиус области а. Аномалия Фая Ag' и гармоники

должны быть вычислены относительно одной и той же нормаль-

ной формулы силы тяжести, соответствующей принятой Нормаль-

ной Земле. При этом значения Ag

находят с помощью формул

(VIII.5)

(VIII.6)

по гармоническим коэффициентам геопотен-

циала. Без вывода приведем формулы для коэффициентов Q

и ()

j Р

(cos яр) S (яр) sin

яр

dяp

(IX.31)

J ^

(tos яр) [5 (яр) - S (яр

)] sin

яр

dip.

aX.32)

Значения (?„ и Q

для значений радиуса Д\р

1000 и

2000

км

приведены в табл. 17. Они (в особенности Q^j быстро убывают

с возрастанием степени гармоники, так что при учете влияния

дальних зон высшая их степень п может быть сравнительно низкой.

Рассмотрим точность определения высот квазигеоида по фор-

мулам (IX.29) и (IX.30). Предположим, что в радиусе Д\р

име-

ется столь точная гравиметрическая съемка, что погрешностями

ее можно пренебречь. Можно также не принимать во внимание

погрешности нулевой гармоники а

= Ау

, поскольку она ока-

зывает равные по величине, но противоположные по знаку влия-

ния на интегральный и дополнительный члены в эти# формулах

и не влияет на их сумму. Тогда с учетом

(VIII.5)

(VIII.6)

получим дифференциальную 'зависимость между погрешностью

£ и погрешностями С

пт

и S

в случае применения формулы

(IX.29)

= -f-22 (

и — 1

)^«

№птcos

mL +

sin

mL) P

(sin Ф).

n=--2

m-o

Таблица

1000

км

i|)

2000

км

Qn Qn

-0,371

-0,369

+1,633

+0,639

+0,311

+0,152

+0,061

+0,004

-0,032

-0,056

-0,070

-0,079

-0,083

—0,083

' .

-0,081

-0,076

-0,071

-0,064

-0,056

-0,048

-0,040

-0,032

-0,024

-0,017

—0,009

-0,178

+1,823

+0,824

+0,492

+0,328

+0,230

+0,166

+0,121

+0,088

+0,064

+0,045

+0,031

+0,020

+0,012

+0,005

0,000

-0,004

-0,007

—0,009

-0,010

-0,729

-0,717

+1,306

+0,338

+0,046

—0,071

-0,118

-0,128

—0,118

—0,097

-0,071

-0,045

-0,020

+0,002

+0,019

+0,030

+0,037

+0,039

+0,036

+0,031

+0,023

+0,014

+0,005

-0,004

-0,011

-0,407

-0,403

+1,604

+0,615

+0,295

+0,145

+0,064

+0,018

—0,008

-0,022

—0,028

—0,025

-0,021

—0,016

—0,010

-0,005

—0,001

+0,002

+0,004

+0,006

+0,005

+0,004

+0,003

Найденное выражение подобно (IX.26). Проведя преобразова-

ния,

аналогичные выводу (IX.27), получим

со

(£) = 2(

)

^»-

(

1Х

)

При вычислении

по

формуле (IX.30) таким

же

образом найдем

оо

СО

= 2

(^Т

)

Ш1

(IX-34)

Л=2

Если выполнить расчеты

по

полученным формулам

исполь-

зованием погрешностей гармонических коэффициентов геопотен-

циала, показанных

на

рис.

63, и

табл.

17, то

найденные значения

(£) не

превысят одного метра. Реальные погрешности будут

больше, хотя

бы

потому,

что при

столь высокой точности нельзя

пренебрегать погрешностями аномалий

области

о.

Однако

полученный результат указывает

на

большие возможности даль-

нейшего уточнения результатов определения высот квазигеоида.

Спутниковый геометрический метод

определения фигуры квазигеоида

В последнее время ценные дополнения

представленным

ре-

зультатам могут быть получены

по

существу геометрическим

методом

— по

данным определений геоцентрических координат

точек земной поверхности

из

динамической обработки наблюде-

ний

ИСЗ и

известным нормальным высотам этих точек. Сущность

этого метода была

по-

казана

в § 51.

Он

уже

нашел при-

менение

при

определе-

нии высот квазигеоида

для станций слежения

за

ИСЗ. С

появлением

портативной допплеров-

ской аппаратуры

по-

явилась возможность

сравнительно быстро

точно получать геоцен-

трические координаты

в полевых условиях.

Такие данные смогут

быть также использо-

ваны для приведения

со-

ставленных карт астро-

номо-геодезических

вы-

сот квазигеоида

к об-

щеземной системе.

Другая возможность

связана

использова-

нием определений геоцентрического радиуса-вектора точек поверх-

ности морей

океанов

помощью спутникового радиовысотомера

(§55).

Дальнейшие вычисления ведут

так

же,

как для

станций сле-

жения

ИСЗ.

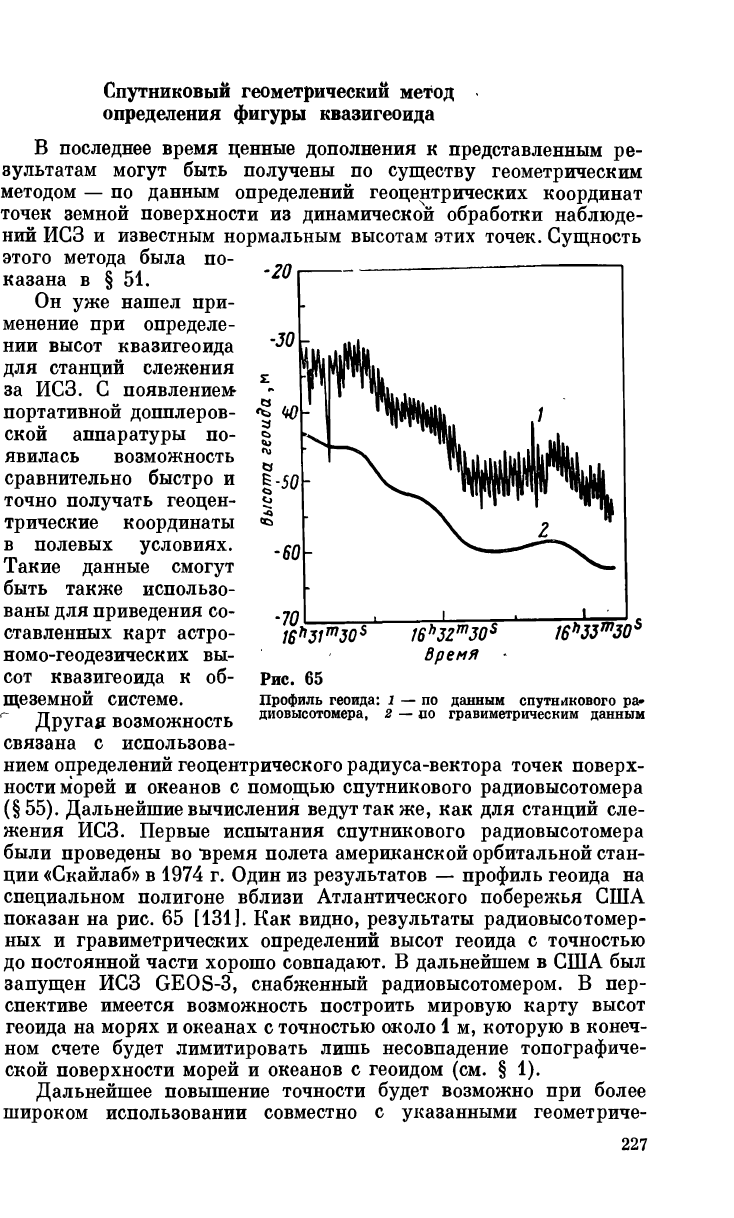
Первые испытания спутникового радиовысотомера

были проведены

во

*время полета американской орбитальной стан-

ции «Скайлаб»

в 1974 г.

Один

из

результатов

—

профиль геоида

на

специальном полигоне вблизи Атлантического побережья

США

показан

на рис. 65

[131].

Как

видно, результаты радиовысотомер-

ных

гравиметрических определений высот геоида

точностью

до постоянной части хорошо совпадают.

дальнейшем

США

был

запущен

ИСЗ

GEOS-3,

снабженный радиовысотомером.

пер-

спективе имеется возможность построить мировую карту высот

геоида

на

морях

океанах

точностью около

1 м,

которую

конеч-

ном счете будет лимитировать лишь несовпадение топографиче-

ской поверхности морей

океанов

геоидом

(см. § 1).

Дальнейшее повышение точности будет возможно

при

более

широком использовании совместно

указанными геометриче-

-20

-7Л

» _J

W*31

16*33

Время

Рис.

Профиль геоида:

1 — по

данным спутникового

ра»

диовысотомера,

2 — цо

гравиметрическим данным

скими данными определений высот

£ из

оптимальной комбинации

детальной гравиметрической съемки

анализа орбитальных

возмущений

ИСЗ.

Только таким путем,

частности, могут быть

выяснены различия топографической поверхности морей

океа-

нов

поверхности геоида.

ГЛАВА

ПЛАНЕТАРНЫЕ ГЕОДИНАМИЧЕСКИЕ

ИССЛЕДОВАНИЯ

62.

ГЕОДИНАМИЧЕСКИЕ ЯВЛЕНИЯ

Прогресс геодезических средств

как

классических,

так и

в особенности новейших космических привел

последние годы

к быстрому развитию исследований

по

изучению изменений

во

времени положений пунктов земной поверхности

элементов

земного гравитационного поля.

Мы уже

отмечали

начале курса

появление нового раздела науки

на

стыке геодезии, геофизики,

астрономии

океанологии

—

геодинамики, которая занимается

вопросами

как

определения указанных выше изменений (будем

их называть геодинамическими явлениями),

так

их

физической

математической интерпретации,

перечисляли

те важнейшие задачи, которые позволит решить геодинамика.

Для удобства последующего изложения классифицируем гео-

динамические явления

по их

спектру

пространстве

времени

(табл.

18).

Будем различать следующие явления

зависимости

от

их

проявления

пространстве:

— глобальные, относящиеся

ко

всей Земле

целом, которая

при

их

интерпретации заменяется некоторой идеальной сравни-

тельно однородной моделью;

— крупномасштабные, относящиеся

областям протяжен-

ностью

—10

км, т. е.

имеющие масштабы континентов

океа-

нов

или

значительных,

их

частей;

— региональные, относящиеся

областям протяженностью

—10

км;

— локальные, относящиеся

областям протяженностью менее

км.

Все явления, кроме глобальных, почти исключительно связаны

с процессами, происходящими

верхней мантии

земной коре.

При этом локальные явления характеризуют

основном про-

цессы, происходящие

верхних слоях земной коры

и на

поверх-

ности Земли,

в том

числе итехногенные, связанные

дея-

тельностью человека. Принятая классификация условна,

так как

нередко крупномасштабные

региональные явления четко про-

являют себя

пределах ограниченных

зон на

границах крупных

Таблица 18

Геодинамические явления

Периоды

их проявления*

Глобальные

Полярное движение

Неравномерность вращения Земли

Изменение положения центра масс и осей инерции Земли

Релятивистские космогонические эффекты

Эвстатическое изменение уровня моря /

Глобальные вариации геопотенциала во времени

Земные и океанические приливы

Крупномасштабные

Движение литосферных плит

Динамические изменения поверхности.морей и океанов

Крупномасштабные вариации геопотенциала во времени

Вариации параметров земных приливов

Региональные

Региональные изменения положений точек земной поверх-

ности

Вариации величины и направления силы тяжести

Локальные

Локальные движения земной коры

Локальные вариации силы тяжести ,

вГм?с?н

ВГМсН

в?г?

в?

вг?

гМС -

Вгм?с?н?

в?г?н?

гМС

Вг?м?Н

в?г?н

Вгм?Н

в?г?н

* Большими буквами отмечены наиболее уверенно определяемые периоды» а те,

существование которых проблематично,—малыми буквами со знаком вопроза.

блоков земной коры, и в этом случае их трудно отделить от фокаль-

ных явлений.

Выделим условно следующие периоды проявления геодинами-

ческих явлений:

— вековые (в),

— годичные или порядка нескольких лет (г),

— месячные, полумесячные (м),

— суточные (с),

— нерегулярные, случайные (н).

Указанными первыми буквами соответствующие периоды- отме-

чены в табл. 18. Заметим, что при современной точности измере-

ний особенно трудно отделить друг от друга вековые и нерегуляр-

ные процессы.

Дадим краткий обзор современных оценок масштабов про-

явления различных геодинамических явлений.

Полярное движение. Движение, под которым пони-

мают перемещение в теле Земли ее оси вращения, было уже рас-

смотрено в § 38 и 39. По сравнению с другими геодинамическими

явлениями оно имеет наибольшую амплитуду, достигающую

18 м или

3-10"

от радиуса Земли (см. рис. 47). Наиболее хорошо

изучены годичная вариация метеорологического происхождения

и Чандлерявское движение с периодом 428 суток, механизм воз-