Пеллинен Л.П. Высшая геодезия (Теоретическая геодезия)

Подождите немного. Документ загружается.

(

уравнения (VIL22)

(VII.23) вместо

g и т]

следует под-

ставить

их

значения, полученные

(VI

1.27).

Если угловые эле-

менты ориентирования заранее

не

известны,

они

будут дополни-

тельными определяемыми величинами

при

решении уравнений

градусных измерений

для

составляющих уклонений отвеса.

Заметим,

что

рассмотренный

эффект

не

имеет места, если

соответствующие

оси

астрономи-

ческой

референцной систем

координат параллельны, хотя

отклоняются

от

осей координат

• общеземной системы.

Уравнения градусных

измерений

при

заданном

Рис

Величину

обычно опреде-

ляют

очень высокой точностью

по зональному гармоническому

коэффициенту

(см. § 37), ко-

торый уверенно выводится

по

вековым возмущениям орбит

ис-

кусственных спутников Земли.

Это

позволяет заранее определить

члены, включающие

Ае

, в

уравнениях градусных измерений.

Кроме того,

настоящее время экваториальный радиус общезем-

ного эллипсоида

а, уже

известен

точностью около

10 м. Это

позволяет заранее рассчитать

погрешностью порядка

3 см

произведение Да-е

/2, входящее

уравнения (VII.21)

(VI

1.22),

в результате свободные члены всех трех уравнений градусных

измерений можно представить

как

Д£

- *1 е

sin

B-^£-a

sin

B(l +

-^sin

д)

;

a sin 2B

(l+e

B);

(VI

1.28)

,Al + —

после чего уравнения приобретают компактную форму

cos В cos L -f-у cos В sin

-f-

z sin В

— Aa —

•=

£sini?cosZ/+ i/sin

sin L

— zcosB

— Z|^0;

(VII.29)

xsinL

—ycosL

—1^—0.

Еще более компактна матричная запись этих трех уравнений

-0, (VTI.30)

г,

ll^

+ Aa.

где R

T э

— матрица поворота от экваториальной системы коор-

динат X, У, Z к горизонтальной X', У, Z', в которой ось Z'

параллельна нормали к референц-эллипсоиду в исследуемой

точке, а ось У параллельна плоскоста ее геодезического ме-

ридиана;

—sin

L cos L О

г_

— sin В cos L — sin В sin L cos В . (VII.31)

- cos В cos L cos В sin £ sin 5

Формула (VII.31) является результатом транспонирования

формулы

(1.18)

в § 2, если в ней положить ф = В, А, = L, и может

быть также непосредственно выведена из рис. 56, на котором

спроектированы на единичную сферу направления осей систем

координат X, У, Z и X', У, Z'.

§ 49. УРАВНЕНИЯ ГРАДУСНЫХ ИЗМЕРЕЙИЙ

ДЛЯ МЕТОДА ПРОЕКТИРОВАНИЯ С ОПРЕДЕЛЕНИЕМ

ВНЕШНИХ ЭЛЕМЕНТОВ ОРИЕНТИРОВАНИЯ

Запишем уравнение (VII.30) для исходного пункта референц-

ной системы координат. Затем, умножив его на матрицу поворота

^г

, э> от горизонтальной системы координат Х'

, У'

в исходном пункте, перейдем к экваториальной X, У, Z

Яэ,

Го#Г

, э

izj

э,

г,

*"Г\

+ Аа_|

(VII.32)

Матрица -йэ, г

может быть получена из

(1.18),

если заменить

Ф на 5о и к на L

. Поскольку Д

г„^г„ з = 1, из уравнения

(VII.32)

с учетом (VII.28) получим

з,г,

ДС

+Аа

Э,Г

•О'

iJc.

(VI

1.33)

В первый член правой части входит вектор элементов, под-

лежащих определению, а второй включает члены, связанные

с эксцентриситетом эллипсоида,

1\ = —**-а sin 2В

(1 + е

sin

);

П =-|^ «

sin

+-^- a

sin

(l +

sin

) ,

которые можно предрассчитать заранее

Достаточной точностью.

Подставив

(VI

1.33) в

уравнения

(VI

1.30),

получим

матричной

записи уравнения градусных измерений

для

внешних элементов

ориентирования

Яг,

э#э,

Го

—

AK]

Д£

+Да

-In

-h

+Aa

—

Яг эЯ

Г, Э-«Э, Го

(VII.34)

В развернутом виде уравнения

для

уклонений отвеса имеют

сложный

вид (см.

[26]),

и мы

ограничимся лишь рассмотрением

уравнений

для

высот квазигеоида. Произведение

, эЯэ, г

может быть записано

как Я

, г

7 что

соответствует непосредствен-

ному переходу

от

системы

Х'

системе

X',

У, Z'.

Исходя

из уравнений

(1.8) в § 2,

найдем

_J^AT,

COS(X

Z')-(^-A^

+/l)cos(yo,

Z')

(A£

+Aa-ll)cos{Z'

Z')-Aa-h

= 0.

(VII.35)

Спроектируем

на

вспомогательную единичную сферу направле-

ния

осейX

о,

Уо, Z

Z', а

также направление

на

полюс

Р.

Обозна-

чив

••=

L — L

, из

решения различных треугольников

на рис. 57

имеем

cos(X

Z') = cos#sin/ = sin:i|)sina;

cos

(Уо,

Z')

= cos Я

sin В

—

sin Я

cos5

cos / = sin

г|>

cos a;

cos

(Z'

Z') = sin B

sin Я + cos B

cos Я cos / = cos if.

Подставив

это в

(VII.35), получим искомое уравнение гра-

дусных измерений

—Мо

sln

<ф

cos a

—

г|)

_j_

Д£

os —

—

Да (1

—cos

г|>) —

' = 0,

где

f£

= /

4-/cCOsip +

Z£sini|?-cosa.

(VII.36)

Как видно,

при

небольших размерах области,

для

точек

ко-

торой составляются уравнения градусных измерений

(а

именно

при

i|> < 90°),

максимальные коэффициенты, близкие

единице,

будут у элемента А^

, поэтому он будет определяться с наиболь-

шей надежностью. При расположении исходного пункта в середине

этой области при первых двух неизвестных будут знакопеременные

коэффициенты, которые в решении достаточно хорошо отделяются

как друг от друга, так и от остальных неизвестных. Минимальный

коэффициент будет у неизвест-

ного Да, которое определяется

грубее всех остальных.

Заметим, что если в свободных

членах уравнений градусных

измерений величины £, £ и т| по-

ложить равными нулю, то из ре-

шения этих уравнений получим

параметры и определим ориенти-

ровку референц-эллипсоида, наи-

более подходящего к исследуемой

территории. Однако при урав-

нивании астрономо-геодезических

сетей методом проектирования и

при наличии референц-эллип-

соида (например, эллипсоида

Красовского), достаточно хорошо представляющего фигуру

Земли, такая постановка задачи потеряла интерес.

Рис. 57

§ 50. ИСПОЛЬЗОВАНИЕ АСТРОНОМО-ГЕОДЕЗИЧЕСКИХ

И ГРАВИМЕТРИЧЕСКИХ ДАННЫХ ПРИ РЕШЕНИИ

УРАВНЕНИЙ ГРАДУСНЫХ ИЗМЕРЕНИЙ

Развитие астрономо-геодезических сетей в XX веке на всех

континентах и широкое развитие мировой гравиметрической

съемки сделало реальными определение параметров общеземного

эллипсоида и привязку к общеземной системе различных рефе-

ренцных систем координат.

После определения эллипсоида Красовского первый такой

вывод был сделан известным английским геофизиком Джеффрисом

в 1948 г. [18, гл. 51. Он оригинальным методом сначала получил

средние радиусы кривизны геоида по ряду протяженных дуг

градусных измерений. В эти результаты были введены поправки

за аномалии силы тяжести с использованием ранее полученного

Джеффрисом разложения силы тяжести по сферическим функциям.

Тем самым были найдены соответствующие радиусы кривизны

общеземного эллипсоида и открылась возможность вывода его

параметров. Было найдено а

= 6 378 103, ± 116 м (отличие от

лучших современных выводов лежит в пределах 40 м) и 1 : а =

296,9

± 0,40.

В 1951 г. М. С. Молоденский разработал теорию вычисления

параметров общеземного эллипсоида, пользуясь разложением силы

тяжести в ряд сферических функций и кривизнами геоида. Последние

находят по результатам градусных измерении с применением

метода площадей [67J. Опыт подобного вывода описан в [21].

Уравнения градусных измерений для метода проектирования

получили применение с развитием как работ по астрономическому

и астрономо-гравиметрическому нивелированию в пределах тер-

риторий континентов, так и мировой гравиметрической съемки.

Чаще всего используют уравнения для высот квазигеоида вида

(VII.21).

Это стало возможным благодаря тому, что абсолютные

высоты квазигеоида мы можем получить с удовлетворительной

точностью на всю поверхность земного шара, пользуясь обоб-

щенным представлением гравитационного потенциала Земли в виде

его разложения по сферическим функциям. Таким образом,уравне-

ния градусных измерений могут быть составлены на любые тер-

ритории, для которых имеются карты астрономо-геодезических

высот квазигеоида. В настоящее время такие карты составлены

примерно на две трети поверхности суши. Уравнения градусных

измерений для уклонений отвеса используют реже, так как для

надежного определения !• и г) требуется детальная гравиметри-

ческая съемка вблизи астропунктов. Чаще всего уравнения

градусных измерений составляют для примерно равновеликих

трапеций, по которым осредняют свободные члены, приписывая

им веса, пропорциональные площадям трапеций.

Возможности использования астрономо-геодезических и грави-

метрических данных при решении уравнений градусных измерений

лучше всего проиллюстрировать на примере определения внешних

элементов ориентирования (§ 49). Пусть на область а, имеющую

форму круга сферического радиуса \р, с исходным пунктом АГС

в центре круга составлены уравнения градусных измерений.

Получим погрешности определяемых параметров для:

а) \j> = 0,25 (14°), что примерно соответствует территориям

США или Австралии;

б) ур = 60°, что примерно соответствует территории Евразии.

Оценки были сделаны как для случая использования лишь

уравнений для высот квазигеоида (решение по Д£), так и для слу-

чая использования также уравнений для уклонений отвеса (ре-

шение по Д£, Д£, Дт]). Веса последних принимались в 10 раз

меньшими по сравнению с уравнениями для высот квазигеоида,

что примерно соответствует реальному соотношению их точности.

Ожидаемые погрешности неизвестных были оценены следующим

образом. Пользуясь уравнением

(VI

1.35),

провели вычисления

для случая, когда величина а

считается известной. При выб-

ранной конфигурации области а в соответствующей нормальной

системе уравнений все не диагональные коэффициенты оказались

равными нулю. В частности, получили

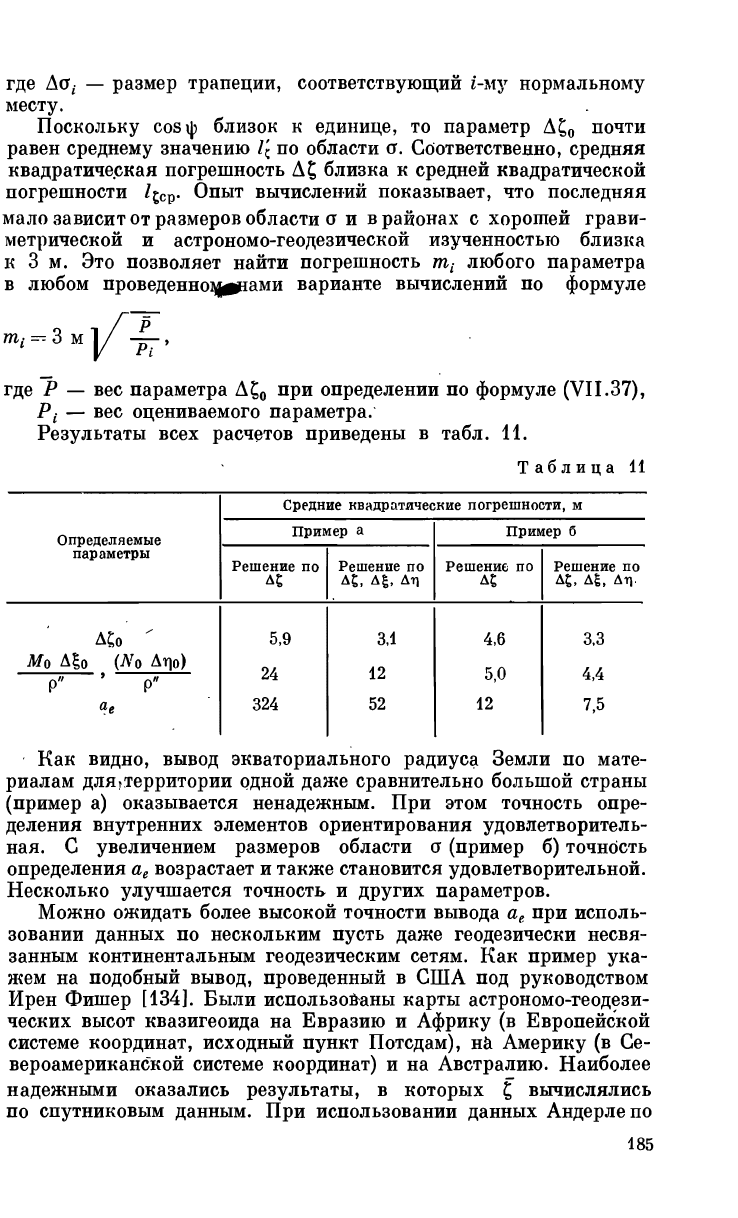
где Да, — размер трапеции, соответствующий i'-му нормальному

месту.

Поскольку

cosij)

близок к единице, то параметр Д£

почти

равен среднему значению 1[ по области а. Соответственно, средняя

квадратическая погрешность Д£ близка к средней квадратической

погрешности /^

ср

. Опыт вычислений показывает, что последняя

мало зависит от размеров области а и в районах с хорошей грави-

метрической и астрономо-гёодезической изученностью близка

к 3 м. Это позволяет найти погрешность ти,- любого параметра

в любом проведенно^од^ами варианте вычислений по формуле

3 м |/"-^-»

где Р — вес параметра Д£

при определении по формуле

(VII.37),

Р;

— вес оцениваемого параметра.

Результаты всех расчетов приведены в табл. И.

Таблица И

Определяемые

параметры

Средние квадратяческие погрешности, м

Определяемые

параметры

Пример а

Пример б

Определяемые

параметры

Решение по

Д£,

Ч>

Решение по Решение по

Д£,

Д£, Ат|-

Мо Д£о (No Дг]о)

р"

' р"

5,9

324

3,1

4,6

5,0

3,3

4,4

7,5

Как видно, вывод экваториального радиуса Земли по мате-

риалам длягтерритории одной даже сравнительно большой страны

(пример а) оказывается ненадежным. При этом точность опре-

деления внутренних элементов ориентирования удовлетворитель-

ная.

С увеличением размеров области а (пример б) точность

определения а

возрастает и также становится удовлетворительной.

Несколько улучшается точность и других параметров.

Можно ожидать более высокой точности вывода а

при исполь-

зовании данных по нескольким пусть даже геодезически несвя-

занным континентальным геодезическим сетям. Как пример ука-

жем на подобный вывод, проведенный в США под руководством

Ирен Фишер [134]. Были использойаны карты астрономо-теодези-

ческих высот квазигеоида на Евразию и Африку (в Европейской

системе координат, исходный пункт Потсдам), н& Америку (в Се-

вероамериканской системе координат) и на Австралию. Наиболее

надежными оказались результаты, в которых £ вычислялись

по спутниковым данным. При использовании данных Андерлепо

анализу допплеровских наблюдений навигационных

ИСЗ США

получено

= 6 378 143 м, а по

данным гравитационной модели

«Стандартная Земля 1966», определенной

по

фотографическим

наблюдениям

ИСЗ, а

= 6 378 145 м. Оба

значения лишь

на 5—

10 м

больше лолучаемых

из

лучших современных выводов

(см.

57).

С развитием других более-выгодных путей определения эква-

ториального радиуса Земли,

которых

мы

будем говорить далее,

изложенный метод градусных измерений сохранит свое значение

при определении элементов ориентирования референцных систем

координат.

При

этом выгодно совместно использовать

все три

вида

уравненир градусных измерений (VII.29)

каждом исследуемом

пункте. Последовательно умножив каждое

из

уравнений

на

коэф-

фициент

в нем при х (или г/, или z), а

затем сложив полученные

произведения, найдем

х —

cos В cos LAa = l

cos В cos L

-\-sin

В cos L -f 1

sin

y — cos5sinLAa = Z

сой

sin L-f sin В sin L

—

cos

(VII.38)

z —

sinBAa

= /

sinZ?

— Z|

cosi?. ,

Как видно, получены линейные зависимости внутренних эле-

ментов ориентирования

х\ i/, z от

поправки

Да.

Если последняя

заранее известна,

то

сразу

по

одной исследуемой точке находим

внутренние элементы ориентирования. Величины

Zg и 1

могут

быть определены

среднем

по 10—20

астрономическим пунктам

в гравиметрически хорошо изученных районах

точностью

по-

рядад

10—20 м.

«Точность

обычно выше

10 м.

Если

в тех же

пределах будет лежать погрешность

представляется реальные

приведение местной системы координат

общеземной системе

с точностью

не

ниже

20 м. *

51.

чисто СПУТНИКОВЫЕГРЕШЕНИЯ УРАВНЕНИЙ

ГРАДУСНЫХ ИЗМЕРЕНИЙ

Возможность использования спутниковых данных

при

решении

уравнений градусных измерений

для

метода проектирования впер-

вые была подчеркнута

А. А.

Изотовым

[32, 80],

который указал,

что

это

относится

не

только

определению величин

£, \ и т],

но

астрономо-геодезических высот квазигеоида

уклонений

отвеса. Предположим,

что

геометрическим спутниковым методом

определены прямоугольные координаты.

X, Y, Z в

некоторой

референцной системе. Выбрав дополнительно референц-эллипсоид

и совместив

его

центр

началом координат,

полярную

ось и на-

чало счета долгот

координатными линиями

Z и X,

можно

по

формулам

§ 2

рассчитать соответствующие эллипсоидальные коор^

динаты

В, L, Н.

Зная астрономические координаты

фД и

нормаль-

ные высоты

№

пунктов спутникового геодезического построения,

легко найти составляющие астрономо-геодезических уклонений

отвеса !•, ц и высоты квазигеоида £. Таким образом, будут полу-

чены все данные для определения свободных членов уравнений

градусных измерений. Поскольку направления осей координат

определяются спутниковым методом независимо от астрономи-

ческих наблюдений, необходимо либо согласовать звездные ка-

талоги и редукции, применяемые в обоих случаях, либо ввести

в число определяемых параметров угловые элементы ориенти-

рования.

Чаще при использовании спутниковых данных задачи опреде-

ления абсолютных элементов ориентирования референцных сис-

тем координат и экваториального радиуса Земли решают раз-

дельно. При решении первой задачи сравнивают прямоугольные

координаты станций наблюдения ИСЗ, полученные в общеземной

системе X, У, ^динамическим спутниковым методом и в рефе-

ренцной сйстем^А, У, Z обычно астрономо-геодезическим ме-

тодом. Вычисления ведутся с использованием формул (VI.44)

в § 41. Как пример в табл. 12 даны значения абсолютных эле-

ментов ориентирования и масштабного множителя т для несколь-

ких референцных систем

координат, полученные в Годдардском

центре космических исследований НАСА США при выводе модели

Земли

GEM-6

[143].

Таблица 12

Элементы

ориентиро-

вания

Система координат

Североаме-

риканская

^Австралийская

Южноамери-

канская

Европейская

я,

У*

z, м

в 10"б

-24 ± 2

151 ± 2

187 ± 2

-0,2 ± 0,5

ОД ± 0,3

—0,8 ± 0,3

1,7 ± 1,2

—135 ± 4

-39 ± 4

133 ± 4

—1,0 ± 0,7

—1,2 ± 0,6

0,4 ± 0,5

2,4 ± 2,2

-63 ± 4

0 ± 4

-32 ± 4

0,6 ± 0,3

-0,2 ± 0,3

0,0 ± 0,4

-1,3 ± 1,2

-83 ± 5

—116 ± 5

—120 ± 6

0,6 ± 0,6

0,4 ± 1,0

-0,6 ± 0,4

—0,3 ± 1,6

Оценка точности выполнена по внутренней сходимости. Отме-

тим, что с учетом возможных систематических погрешностей

точность линейных внутренних элементов ориентирования, полу-

ченных по лучшим современным данным, даже для такой системы

координат, как Североамериканская, в которой известно Положе-

ние большого числа станций наблюдения ИСЗ, лежит в пределах

10 м. Угловые элементы определяются неуверенно даже по внут-

ренней сходимости. Фактически трудно говорить об определении

единых элементов ориентирования для больших наземных астро-

номо-геодезических построений, поскольку ошибки передачи

координат наземными методами по исследованиям за рубежом

обычно превышают ошибки элементов ориентирования.

После того как динамическим спутниковым методом получены

прямоугольные координаты станций наблюдений ИСЗ относительно

центра масс Земли, можно по формулам в,§ 2 найти их геодези-

ческие высоты Н относительно некоторого выбранного эллип-

соида, центр которого совмещен с центром масс Земли, а сжатие

согласовано с определениями гармонического коэффициента /

по спутниковым данным и совпадает со сжатием общеземного

эллипсоида. Зная нормальные высоты Н

указанных станций,

можно получить соответствующие значения £, аналогичные в урав-

нениях градусных измерений астрономо-геодезическим,

Если, используя высоты £ над общеземным эллипсоидом, опре-

деленные из оптимальной комбинации гравиметрических и спут-

никовых данных, составить уравнения градусных измерений для

высот квазигеоида (VII.21) в § 48, то в них величины х, у, z

и Ае

будут равны нулю. Тогда с учетом уравнения

(VI

1.16)

получим

Возникает возможность определить а

по данным лишь одной

станции наблюдения ИСЗ!

В настоящее время нетрудно получить разности £ — £ для

многих пунктов со средними квадратическими погрешностями

771д

порядка 5—10 м. При наличии 50 таких пунктов будет до-

стигнута по формальным оценкам точность определения а

порядка

1—2 м. Фактически из-за масштабных искажений, которые

несколько неожиданно оказались свойственными динамическим

спутниковым методам определения геоцентрических координат,

эти погрешности достигают 5 м и более.

Перспективы последующего повышения точности спутниковых

выводов связаны как с повышением точности самого спутникового

метода, так и в особенности с привлечением данных, получаемых

другими новейшими космическими методами.

На XVI Генеральной ассамблее Международной ассоциации

геодезии в 1975 г. в Гренобле (Франция) было рекомендовано

значение а

как результат ряда спутниковых выводов, лещащих

в пределах от 6 378 130 до 6 378 144 м. Компромиссный вывод

6 378 137 м был округлен до 6 378 140 м и с приписанной «реали-

стической» погрешностью 5 м признан наиболее представитель-

ным [133].

(VI

1.39)

(VI

1.40)

ГЛАВА

VIII

МЕТОДЫ И РЕЗУЛЬТАТЫ ОПРЕДЕЛЕНИЯ

ФУНДАМЕНТАЛЬНЫХ ПОСТОЯННЫХ,

ХАРАКТЕРИЗУЮЩИХ ВНЕШНЕЕ

ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ

§ 52. ОПРЕДЕЛЕНИЕ ЭКВАТОРИАЛЬНОЙ СИЛЫ ТЯЖЕСТИ

До появления искусственных спутников Земли экваториальную

силу тяжести у

получали путем обработки измерений силы тя-

жести на физической поверхности Земли. Строгая теория опре-

деления у

по этим данным была создана М. С. Молоденским [69].

Однако погрешности, вносимые главным образом недостатком

гравиметрических данных и их неравномерным распределением

по площади и по высоте, мешали получению уверенных выводов.

Поэтому большинство исследователей, занимавшихся определе-

нием системы фундаментальных геодезических постоянных, либо

совсем не использовали определения у

по гравиметрическим

данным, либо придавали им небольшой вес.

Новая ситуация сложилась в настоящее время. На обширных

территориях

ПОЛУЧИЛИ развитие детальные гравиметрические

съемки, хорошо Привязанные с помощью мировой опорной грави-

метрической сети к пунктам абсолютных измерений силы тяжести.

Надежно определены динамическим спутниковым методом гар-

монические коэффициенты геопотенциала низких степеней. Это

позволяет успешно применять метод получения экваториальной

силы тяжести из комбинации гравиметрических и спутниковых

данных. В этом параграфе изложим один из таких методов, в ко-

тором совместно со спутниковыми данными используют измерения

силы тяжести лишь в гравиметрически хорошо изученных районах.

Другой метод будет рассмотрен в § 60.

Связь аномалий Фая и гармонических

коэффициентов геопотенциала

Получим некоторые зависимости, которые нам понадобятся

в последующем изложении. Пользуясь выводами в § 35, предста-

вим возмущающий потенциал Т = V — V

во внешнем простран-

стве в виде разложения по шаровым функциям геоцентрических

координат. Будем полагать, что нормальный потенциал притя-

жения V

соответствует Нормальной Земле, которая выбрана под

условиями, сформулированными в § 35. Напомним, что все гар-

монические коэффициенты нормального потенциала притяжения,

кроме, четных зональных о» С*, (>•••» равны нулю. Записав

в виде, аналогичном уравнению

(VI.

1), и образовав разность

V — F

, получим

ОО

=:1

Т~

2 2

(т*)"

(

AC>

"»

C0S mL

™

Sln

)

(Sin

Ф),

2 771

(VIII.l)

189