Пеллинен Л.П. Высшая геодезия (Теоретическая геодезия)

Подождите немного. Документ загружается.

Как видно, большое значение при передаче координат по

звеньям имеют погрешности выходных сторон и в особенности

азимутов Лапласа. Из-за этого довольно заметна корреляция

ошибок соседних звеньев. Наличие такой корреляции приводит

к увеличению погрешностей на 1 км ряда и соответственно по-

грешностей передачи координат по сравнению с оценками, в ко-

торых этой корреляцией пренебрегают, на 25% в продольных

и на 30% в поперечных сдвигах. С таким явлением нельзя не

считаться при строгом уравнивании астрономо-геодезической сети.

Погрешности на 1 км ряда для АГС СССР оказываются сле-

дующими:

продольный сдвиг \i

= ±5,3

CM/|/S

;

поперечный сдвиг \i

'= ±9,6

CM/J/"S

;

радиальный сдвиг

JLL^

= ±3,0 см/

Если по этим значениям построить эллипсоид погрешностей,

то он окажется сильно вытянутым в поперечном направлении

к ряду, а наименьшей окажется его полуось в радиальном направ-

лении. Как видно, высокие требования к определению астрономо-

геодезических высот квазигеоида, вытекающие из применения

метода проектирования и положенные в основу работ по астро-

номо-гравиметрическому нивелированию в СССР, привели.к тому,

что передача радиальных координат осуществляется с некоторым

запасом точности по сравнению с плановыми координатами. Да-

лее мы увидим, что это имеет положительное значение при раз-

работке методов уравнивания астрономо-геодезической сети СССР.

Если-на основе полученных значений погрешностей сдвигов,

приходящихся на 1 км, рассчитать точность ошибки передачи

координат на расстояние порядка

5000

км, то по формулам (V.14)

найдем

тпр

= ±3,7 м;

rriQ=

±6,8 м; mg-= ±2,1 м. '

Как видно, оценка точности АГС СССР до уравнивания полу-

чается вполне удовлетворительной. Во всяком случае найденные

погрешности оказались существенно меньше тех, которые полу-

чены сходным методом для протяженных зарубежных астрономо-

геодезических сетей, в том числе сети США до ее укрепления

высокоточными светодальномерными ходами. По оценкам Л. Сим-

монса [142], полученные из анализа координатных невязок

полигонов триангуляции 1 класса относительные погрешности

передачи координат на расстояние L выражаются эмпирической

формулой

У™%

™%

~ 25

ооо

™

(мы перевели эту формулу в метрическую систему). Для расстоя-

ния

5000

Км имеем

Virtp

+ т\ = 11,9 м, что заметно ниже точ-

ности нашей сети (соответствующая величина в которой равна

±7,7 м). ' . '

§ 29. ТОЧНОСТЬ ПЕРЕДАЧИ КООРДИНАТ НА БОЛЬШИЕ

РАССТОЯНИЯ С УЧЕТОМ ВЗАИМНОГО ВЛИЯНИЯ

ПОГРЕШНОСТЕЙ ПЛАНОВЫХ ЭЛЕМЕНТОВ АГС

И ВЫСОТ КВАЗИГЕОИДА

Качественная оценка косвенных эффектов при условии при-

менения метода проектирования уже была дана в § 26. Рассмот-

рим теперь эти эффекты более тщательно для ряда триангуляции

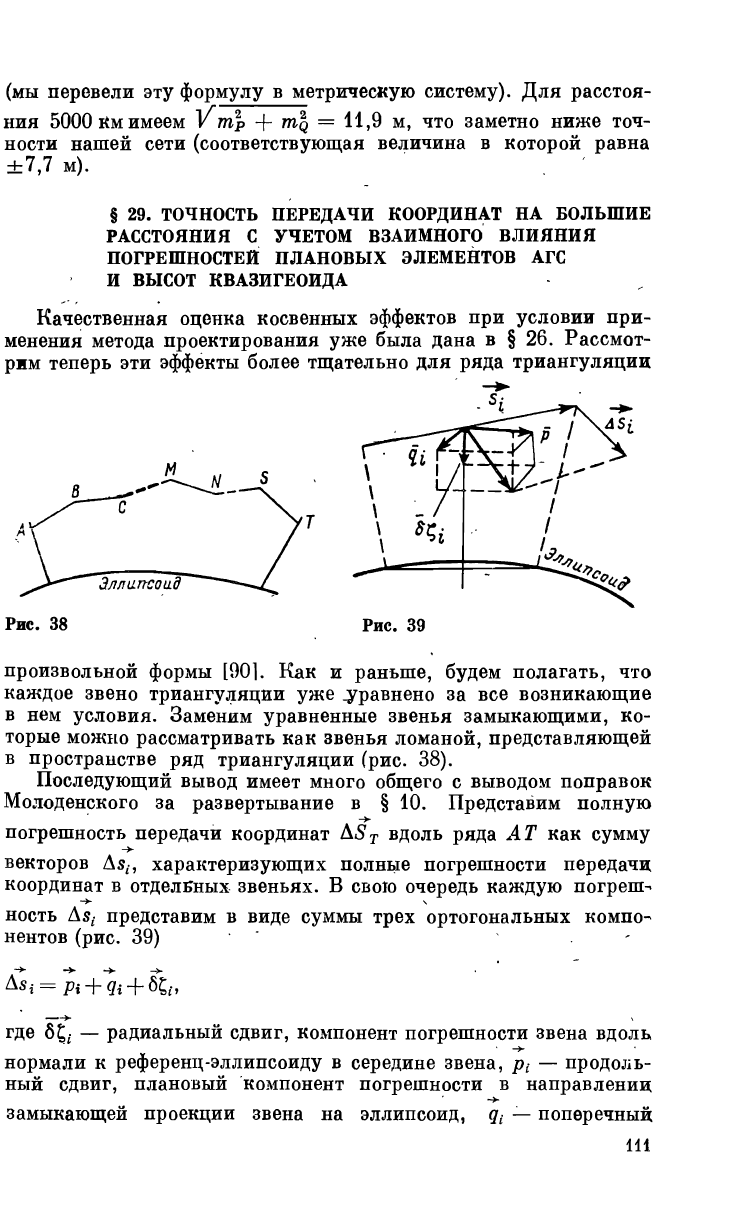
Рис. 38

Рис. 39

произвольной формы [901. Как и раньше, будем полагать, что

каждое звено триангуляции уже .уравнено за все возникающие

в нем условия. Заменим уравненные звенья замыкающими, ко-

торые можно рассматривать как звенья ломаной, представляющей

в пространстве ряд триангуляции (рис. 38).

Последующий вывод имеет много общего с выводом поправок

Молоденского за развертывание в § 10. Представим полную

->-

погрешность передачи координат AS

вдоль ряда AT как сумму

векторов As

характеризующих полные погрешности передачи

координат в отдельных звеньях. В свою очередь каждую погреш-

ность As{ представим в виде суммы трех ортогональных компо-

нентов (рис. 39) -

где 6£

{

- — радиальный сдвиг, компонент погрешности звена вдоль

нормали к референц-эллипсоиду в середине звена, p

— продоль-

ный сдвиг, плановый компонент погрешности в направлении

замыкающей проекции звена на эллипсоид, q

— поперечный

сдвиг, плановый компонент погрешности

азимутальном напра-

—>-

влении,

6£j —

радиальный компонент,

он

практически целиком

обусловлен погрешностью передачи высоты квазигеоида

звене.

Таким образом,

(V.19)

Составляющую погрешности конечной точки ряда

любом

направлении

можно получить

как

проекцию векторного соотно-

шения

(V.

19).

на это

направление

A£r*

= S[PiCqs(p,, s) + gfCos(g„ х) +

6£,

cos (h

, х)].

(V.20)

Если выделить

точке

радиальное направление

, а

также

ортогональные

ему

горизонтальные широтное

долготное

на-

правления,

то три

возникающих уравнения вида (V.20) можно

записать

матричном виде

8LT

COS

ВТ'

8В

2)Д|

(V.21)

где

—

матрица поворота

от

горизонтальной системы коор-

динат

(qi, pi, h

) в

середине

i-то

звена

выбранной горизонталь-

ной системе

точке"

Г (см. § 2).

Наиболее просто формулы

для

расчета погрешностей передачи

координат

учетом косвенных влияний могут быть записаны

для

частного случая вытянутого ряда

из п

звеньев. Необходимые

углы между координатными осями можно получить

из рис. 20

§ 10. Из

формулы (V.20) будем иметь

%т

= 2

(Pt

sin

%г cos

);

т = 2 (Pi cos

ургт

—

sinter);

г=1

(V.22)

Предположим сначала,

что все

погрешности, входящие

в эти

формулы, случайны

независимы. Тогда, применяя обычные

правила квадратирования

полагая,

что

средние квадратические

продольные, поперечные

радиальные погрешности

для

всех

звеньев соответственно равны

, т

т%, найдем

= т£ 2

sin

+ т\

2cos

;

г=1

= ml 2 cos

г|)г

+ 2

sin

;

г=1

= m

(V.23)

Возможную корреляцию погрешностей соседних звеньев

те-

перь нетрудно

достаточной точностью учесть, если заменить

в формуле (V.23)

на т\ (1 + 2г

), а т\ на т\ (1 + 2r

Тогда,

используя (V.13)

в § 27, мы

сможем представить (V.23)

виде

™z

sin2

4'ir + 2 cos

;

1=1

w|>

jipS

2 cos

i|)i

fxfs

sin

'Фгт;

i=l

(V.24)

Используем приближенные соотношения:

2cos

i|)

^^-

cos

^A|>

= "

(r+l^r

*^);

i=l

. "ФАГ

^Sin

^^^-;

81п»фЛ[>

1»

^__1_

1п2*

АГ

)

i»l

Принимая

во

внимание,

что ns = L =

R^AT>

найдем

2 r

IUQ

= \lqb.

Сравнивая этот результат

формулами

(V.

14)

в § 27 для

оценок «прямых» погрешностей, приходим

выводу,

что

полная

погрешность положения конечного пункта ряда, равная

(/raj +

тр +

WIQ)

1/2

обоих случаях одинакова. Косвенные эффекты

приводят лишь

перераспределению продольных

радиальных

ИЗ

погрешностей, а именно из тпр, найденного по формулам (V.14),

вычитается член

(rf

ft")

(т - т

sin

тг) =

™>

(v-

)

который прибавляется к т\. Поскольку в АГС СССР jxp > р,;,

то из-за косвенных эффектов радиальная составляющая в погреш-

ности передачи координат в вытянутом ряду триангуляции уве-

личивается, а продольная уменьшается.

В табл. 6 приведены оценки продольных, поперечных и ра-

диальных сдвигов в пунктах ряда триангуляции, проложенного

по дуге большого круга, для различных сферических расстояний

LIR

в предположении, что погрешности на 1 км хода имеют зна-

чения, полученные нами по данным для АГС СССР в § 28. Как

видно, косвенные влияния ощутимо проявляются при дугах

длиною более 20°. Наиболее заметно эти влияния проявляются

в радиальном сдвиге —-при дугах длиной более 40° вклад в него

продольных ошибок звеньев становится больше вклада ошибок

превышений квазигеоида.

Заметим, что полученные нами результаты в полной мере спра-

ведливы лишь в том случае, когда ходовыми линиями при вычисле-

нии превышений квазигеоида выбраны те, по которым велась

передача плановых координат. Строго говоря, необходимо, чтобы

при вычислении превышения квазигеоида и приращений плановых

координат в пределах каждого звена триангуляции принимали за

исходные в начальной точке звена одно и то же значение высоты

квазиГеоида и одни и те же плановые координаты. Это возможно

при последовательной обработке звена за звеном, начиная от

выбранного исходного пункта АГС [75]. Фактически, учитывая

достаточно высокую точность астрономо-гравиметрического ниве-

лирования, приемлемо проведение подобного поэтапного вы-

числения не по звеньям, а по рядам и блокам триангуляции такой

протяженности, при которой косвенные влияния погрешностей

астрономо-гравиметрического нивелирования на передачи пла-

новых . координат и обратные влияния (их суммарный эффект

дает величина m

) оставались бы пренебрегаемо малыми. Судя

по данным табл. 7, протяженность указанных рядов или блоков

должна находиться в пределах LIR = 40°.

С полной последовательностью изложенный порядок вычисле-

ний не выдерживался при развитии больших астрономо-геодези-

ческих сетей, в том числе и в нашей стране. Поэтому необходим

специальный анализ исполненных сетей до их общего уравнивания

с целью согласования используемых в этом уравнивании началь-

ных геодезических координат и высот квазигеоида. Возможной

альтернативой изложенного порядка вычислений является метод

пространственной обработки больших астрономо-геодезических

сетей, который изложен в § 32.

Таблица 7

Составляющие погрешности ряда, м

Сферические расстояния

Составляющие погрешности ряда, м

20° | 40°

60° 80° | 100°

Продольный сдвиг ряда:

Влияние продольных сдвигов звеньев

Косвенное влияние погрешностей при-

ращений высот квазигеоида

Суммарный продольный сдвиг ряда тр

Оценка без учета косвенных эффектов

Поперечный сдвиг ряда

rriQ

Радиальный сдвиг ряда:

Влияние погрешностей приращений вы-

сот квазигеоида

Косвенное влияние продольных сдвигов

звеньев

Суммарный радиальный сдвиг ряда m

Оценка без учета косвенных эффектов

Величина m

[формула

(V.26)]j

2,45

0,28

2,47

2,50

4,53

1,39

0,50

1,47

1,41

0,41

3,26

0,77

3,35

3,53

6,40

1,84

1,36

2,29

2,00

1,13

3,64

1,33

3,87

4,33

7,84

2,06

2,34

3,12

2,45

1,93.

3,74

1,87

4,19

5,00

9,05

2,12

3,31

3,93

2,83

2,73

3,75

2,34

4,43

5,59

10,12

2,12

4,14

4,65

3,16

3,41

§ 30. ОБЩИЕ ПРИНЦИПЫ ПОЛИГОНАЛЬНОГО МЕТОДА

УРАВНИВАНИЯ АСТРОНОМО-ГЕОДЕЗИЧЕСКИХ СЕТЕЙ

Уравнивание обширных астрономо-геодезических сетей яв-

ляется заключительной стадией их создания. При надлежащей

постановке оно позволяет наилучшим образом решить главные

задачи развития АГС — распространение на большие территории

единой системы геодезических координат и создание основы

для развития последующих геодезически^ построений. Работы

по уравниванию позволяют устранить невязки в сети, возни-

кающие за счет избыточных измерений, повысить точность сети

благодаря оптимальному использованию последних и, наконец,

дать оценку этой точности.

Наибольшее распространение в прошлого получил полигональ-

ный метод, что соответствовало первоначальному развитию про-

тяженных геодезических сетей как полигональных построений.

В конце XIX века известный немецкий ученый-геодезист Ф. Гель-

мерт, рассматривая задачу уравнивания обширных сетей как

органическую часть исследований фигуры Земли, разработал

метод уравнивания астрономо-геодезической сети, созданной в

виде полигонов и обработанной методом развертывания, с одно-

временным определением исходных геодезических дат и пара-

метров референц-эллипсоида, наиболее подходящих к уравни-

ваемой сети. Подробно метод Гельмерта изложен Ф. Н. Красов-

ским в [46]. Из-за громоздкости

этот метод не нашел широкого

практического приложения (им" были обработаны лишь восемь

полигонов), но оказал заметное влияние на последующее развитие

исследований по вопросам уравнивания. Почти во всех суще-

ствующих вариантах полигонального метода применяются, так

же как и в методе Гельмерта, следующие три этапа:

1) предварительное уравнивание звеньев триангуляции с вы-

числением в результате этого длин и азимутов отрезков геодези-

ческих линий, являющихся замыкающими звеньев;

2) уравнивание полигонов геодезической сети- с использова-

нием полученных элементов замыкающих, которые рассматри-

ваются как непосредственно измеренные величины;

3) вставка звеньев путем их вторичного уравнивания между

узлами полигонов, положение которых получено в этапе 2.

При практическом выполнении уравнивания больших геодези-

ческих сетей за рубежом долгое время господствовал чисто ути-

литарный подход к этой операции, как к необходимому согла-

сованию результатов измерений, которое может быть проведейо

достаточно приближенно с применением простейших средств.

Наибольшую популярность за рубежом получил метод аме-

риканского геодезиста Бруи, примененный при уравнивании три-

ангуляции США в 1929 г. Как и во многих других методах по-

лигонального уравнивания, в нем реализованы указанные выше

три этапа вычислений, причем в этапе 2) при совместном уравни-

вании полигонов коррелатным методом в качестве измеренных

величин приняты разности долгот или широт узлов полигонов

с весами, обратно пропорциональными длинам сторон звеньев.

Использованы лишь координатные условия в полигонах. В ре-

зультате нормальная система уравнений распадается на две

независимые идентичные системы, в одну из которых входят

невязки широтных уравнений и поправки разностей широт узлов

полигонов, а в другую — соответствующие долготные соста-

вляющие. В измененном виде метод Боуи был применен в 1949 г.

для приближенного уравнивания геодезических сетей Западной

и Центральной Европы. Результаты этого уравнивания ныне

признаются недостаточно удовлетворительными, и уже много лет

геодезисты стран Западной Европы в рамках специальной комис-

сии Международной ассоциации геодезии ведут подготовку к но-

вому более строгому уравниванию геодезических сетей этих стран.

В СССР всегда господствовало стремление получить уравнен-

ные элементы астрономо-гёодезической сети с максимально воз-

можной точностью и с ослаблением влияния на них не только

случайных, но и по возможности различных систематических

погрешностей. В принципе возможно обработать любую самую

обширную сеть триангуляции по всей строгости метода наи-

меньших квадратов с включением в уравнивание непосредственно

измеренных величин на пунктах государственных геодезических

сетей не только первого, но и последующих классов. Однако такой

путь обработки до сих пор не осуществлен ни в одной стране.

В нашей стране это было связано со следующими обстоятель-

ствами.

Работы по созданию полигонов триангуляции, а в даль-

нейшем и полигонометрии 1 класса опережали развитие работ

последующих классов из-за необходимости сравнительно быстро

распространить единую систему геодезических координат на

обширные территории. Возникала потребность в уравнивании

полигонов 1 класса для упорядочения результатов этих перво-

классных работ.

2. Задача уравнивания как одного целого сплошных геоде-

зических построений на обширных территориях весьма сложна

даже при использовании электронно-вычислительных машин (до-

статочно упомянуть, что в нашей стране ныне речь идет о сов-

местной обработке многих десятков тысяч пунктов), а прежде

• при использовании настольных вычислительных машин пред-

ставлялась вообще неразрешимой. Трудности возникают не только

из-за большого объема вычислений, но и из-за неизбежного риска

допустить погрешности как в ходе самих вычислений, так и в.пе-

риод подготовки к ним необходимой информации. Вероятность

таких погрешностей быстро возрастает и приближается к единице

с увеличением объема совместно обрабатываемых данных.

3. Даже если бы и удалое^ совместно уравнять обширное

геодезическое построение со всей формальной строгостью метода

наименьших квадратов, полученный результат мог оказаться

не оптимальным из-за отличия реальной структуры погрешностей

измерений от нормального закона Гаусса и пренебрежения кор-

реляционными связями этих погрешностей. При этом наибольшие

искажения будут внесены в оценку точности полученных резуль-

татов.

Указанные обстоятельства заставляли идти на применение

менее строгого полигонального метода уравнивания. В нашей

стране многие слабости этого метода были устранены тем,-что

при создании АГС была последовательно выдержана разработан-

ная Ф. Н. Красовским полигональная схема ее построения.

Применительно к этой схеме Ф. Н. Красовским и другими уче-

ными были разработаны несколько вариантов полигонального

метода уравнивания АГС, в которых были удачно использованы

особенности построения сети,

|§ 31. УРАВНИВАНИЕ АСТРОНОМО-ГЁОДЕЗИЧЕСКОЙ

СЕТИ СССР ПОЛИГОНАЛЬНЫМ МЕТОДОМ

Первое уравнивание АГС СССР

В основе всех работ по полигональному уравниванию АГС

СССР лежат принципы метода уравнивания, разработанного

Ф. Н. Красовским с использованием некоторых идей метода

Гельмерта. Однако в отличие от него Красовский, сохранив стро-

гость решения, отделил задачу уравнивания от задачи установле-

ния исходных геодезических дат и размеров подходящего

референц-эллипсоида и тем самым упростил решение, сделав его

практически реализуемым.

Первый вариант предложений Красовского был применен

при уравнивании девяти полигонов АГС СССР в

1930—1932

гг.

В этом варианте еще предполагалось, что наиболее подходящие

исходные геодезические даты

и элементы референц-эллипсоида

установлены настолько удовле-

творительно, что можно исполь-

зовать данные обработки триан-

гуляции методом развертывания.

На первом этапе из уравнива-

ния звеньев за все возникающие

в них условид определяли и в даль-

нейшем принимали за «измерен-

ные» длины геодезических линий s

между концами звеньев (обычно

узлами полигонов) и углы (5

между измеренными направле-

ниями азимута Лапласа в каждом

узле полигона и направлениями

замыкающих звеньев (рис. 40,

на котором изображен типовой

полигон

1—2—3—4).

На втором этапе выполняли совместное

уравнивание коррелатным методом всех полигонов, принимая во

внимание координатные условия широты и долготы для каждого

полигона и азимутальное условие для каждого звена.

Вывод координатных условий был проведен Красовским,

исходя из известных в сфероидической геодезии дифференциаль-

ных формул первого рода. Отсылая интересующихся к работам

Красовского [43, 44], ограничимся далее изложением его вывода

азимутального условия.

После перехода от звеньев к их замыкающим оно может быть

получено для некоторого звена ik (см. рис. 40) следующим об-

разом. Пусть на концах звена выполнены астрономические опре-

деления азимутов Лапласа A

и А

, разность которых в соответ-

ствии с уравнением Лапласа (§ 7) имеет вид

(А

)

UCf?

= а

- щ - (к

— L

) sin B

+ (А,, - L

) sinB

. '(V.27)

Однако, с другой стороны, та же разность может быть опреде-

лена путем решения прямой геодезической задачи в звене ik:

Рис.

{

— А ;)геод = (hi — P/ft) + (A

(V.28)

Результаты вычислений по формулам (V.27) и (V.28) должны

совпадать, т. е. азимутальное условие может быть записано в виде

= (А

—

Л/)астр

- Uk -

4;)геод

= 0.

118

(V.29)

Красовский путем тщательных исследований показал, что

поправки принятых геодезических координат B

L,, B

, L

и раз-

ности A

— A

пренебрегаем о мало влияют на азимутальное

условие. Поэтому, варьируя условием (V.29), получим с учетом

(V.27) и (V.28) -

§F\h = fih =

- 8X

sin B

- 8a

6X,sinft-v

+ v

(V.30)

где

=6p^.

Все полученные условные уравнения

решались коррелатным методом под усло-

вием

IpM

+ [p

] +

]

+ [р

№] = min,

Рис

где p

, p

и px — веса «измеренных»

величин 5, р, а и Я.

Как видно, сохранив контролирующее значение азимутов

Лапласа на стадии уравнивания звеньев, в дальнейшем Красов-

ский предлагал определять поправки к астрономическим азимутам

и долготам. Последним этапом полигонального уравнивания была

вставка отдельных рядов и звеньев между вершинами полигонов.

Однако в пересечении рядов одни и те же треугольники входят

в разные звенья и их углы или направления могут получить не-

одинаковые поправки из вставки разных звеньев между узлами

полигонов. Чтобы избежать этого, на стыке звеньев выделяли

узловые фигуры таким образом, чтобы смежные звенья не имели

общих направлений (рис. 41)

и сначала уравнивали эти фигуры,

а затем, принимая их элементы окончательными, уравнивали

оставшиеся части звеньев.

Второе уравнивание АГС

При втором уравнивании астрономо-гёодезической сети СССР

1941—1945

гг. были совместна обработаны методом Красовского

87 полигонов, включавшие в себя 310 звеньев. По своим масшта-

бам и тщательности исполнения эта работа, проведенная в годы

Великой Отечественной войны и направленная на решение' гран-

диозных задач восстановления и развития народного хозяйства

в последующие мирные годы, не имела себе равных в мире. В про-

цессе подготовки к непосредственному уравниванию была проде-

лана большая работа по выводу нового референц-эллипсоида Кра-

совского, установлению новых исходных дат в системе 1942 г.

(см.

§ 47 главы VII), астрономо-гравиметрическому нивелирова-

нию (см. главу TV), проектированию всех измерений на поверх-

ность эллипсоида Красовского, введению в астрономические опре-

деления поправок за движение полюса и других редукций. В этих