Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffraction

Employing a high quality standard sample (e.g. LaB6, see the footnote on

page

156)

that has no measurable contributions from small crystallite size

and microstrains, the peak shape function parameters

(U,

Wand

P),

responsible for the instrumental and wavelength dispersion broadening,

can be determined experimentally. These should remain constant during

following experiments when using different materials and, thus should be

kept fixed in future refinements. Obviously, the goniometer configuration

must be identical in the experiments conducted using both the standard

and real samples. This method requires measuring a standard every time

when any change in the experimental settings occurs, including

replacement of the x-ray tube, selection of different divergence or

receiving slits, monochromator geometry, filter, and other.

Taking advantage of the fundamental parameters approach, which is

based on a comprehensive description of the experimental conditions and

hardware configuration. It is developed quite well and as a result, the

corresponding peak shape parameters may be computed and not

necessarily refined. This technique requires realistic data about the

experimental configuration, such as slit openings and heights, in-plane

and axial divergences, monochromator characteristics, source and sample

geometry and dimensions, and other. Indeed, considerable effort is

involved in order to obtain all required physical characteristics of the

powder diffractometer, the source and the specimen. The resultant peak

shape is then obtained as a convolution (Eq.

2.45)

of the modeled

instrumental function, wavelength distribution in the incident spectrum,

and sample function, with the pseudo-Voigt function.' The fundamental

parameters approach is implemented in several software products,

including Koalariet/XFIT2 and

BGIvIN.~

More detailed information about

both the technique and its implementation may be found in the

corresponding

reference^.^,^

From this point of view, some applications of the modified pseudo-Voigt function (e.g.

third and fourth peak shape functions employed in GSAS) are in a way similar to the

fundamental parameters approach as they use instrumental parameters to describe certain

aspects of peak shape.

See

http://www.ccpl4.ac.uWtutorial/xfit-95Ixfit.htm.

See http:/h.bgmn.de/.

R.W. Cheary and A. Coelho. A fundamental parameters approach to X-ray line-profile

fitting,

Appl. Cryst.

25,

109 (1992);

R.W.

Cheary and A.A. Coelho. Axial divergence in

a conventional x-ray powder diffractometer.

11.

Realization and evaluation in a

fundamental-parameter profile fitting procedure,

Appl. Cryst.

31,

862 (1998).

Bergmann,

Kleeberg, A. Haase, and B. Breidenstein. Advanced fundamental

parameters model for improved profile analysis, Mater. Sci. Forum

347,

303 (2002) and

references therein.

182

Chapter

2.9.2

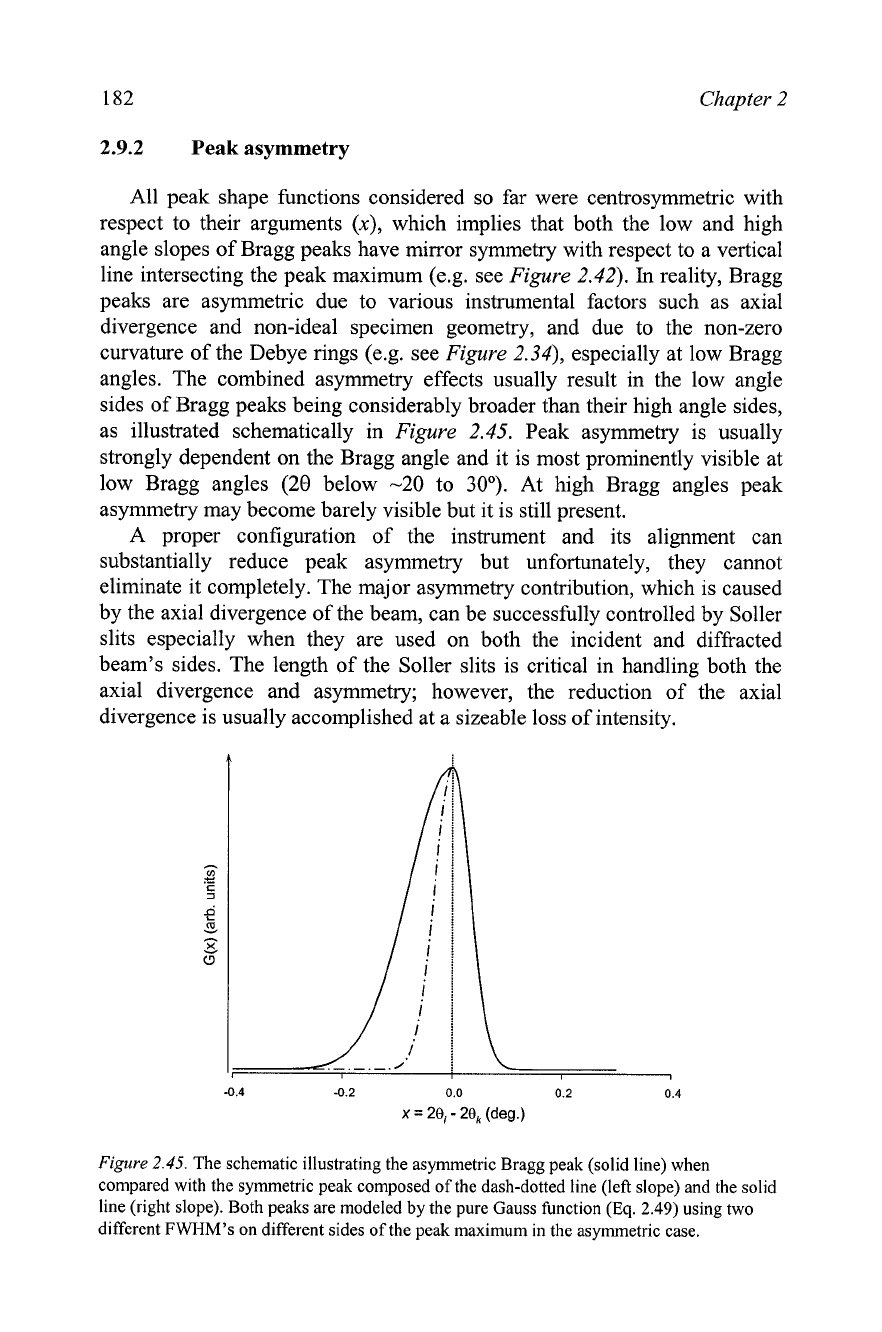
Peak asymmetry

All peak shape functions considered so far were centrosymmetric with

respect to their arguments

(x),

which implies that both the low and high

angle slopes of Bragg peaks have mirror symmetry with respect to a vertical

line intersecting the peak maximum (e.g. see

Figure

2.42).

reality, Bragg

peaks are asymmetric due to various instrumental factors such as axial

divergence and non-ideal specimen geometry, and due to the non-zero

curvature of the Debye rings (e.g. see

Figure

2.34),

especially at low Bragg

angles. The combined asymmetry effects usually result in the low angle

sides of Bragg peaks being considerably broader than their high angle sides,

as illustrated schematically in

Figure

2.45.

Peak asymmetry is usually

strongly dependent on the Bragg angle and it is most prominently visible at

low Bragg angles

(20

below

-20

30').

At high Bragg angles peak

asymmetry may become barely visible but it is still present.

A proper configuration of the instrument and its alignment can

substantially reduce peak asymmetry but unfortunately, they cannot

eliminate it completely. The major asymmetry contribution, which is caused

by the axial divergence of the beam, can be successfully controlled by Soller

slits especially when they are used on both the incident and diffracted

beam's sides. The length of the Soller slits is critical in handling both the

axial divergence and asymmetry; however, the reduction of the axial

divergence is usually accomplished at a sizeable loss of intensity.

-0.4 -0.2 0.0 0.2 0.4

20,

(deg.)

Figure

2.45.

The schematic illustrating the asymmetric Bragg peak (solid line) when

compared with the symmetric peak composed of the dash-dotted line (left slope) and the solid

line (right slope). Both peaks are modeled

the pure Gauss function

(Eq.

2.49)

using two

different FWHM's on different sides of the peak maximum in the asymmetric case.

Fundamentals

diffraction

183

Since asymmetry cannot be completely eliminated, it should be addressed

in the profile fitting procedure. Generally, there are three ways of treating

the asymmetry of Bragg peaks, all achieved by various modifications of the

selected peak shape function:

the first method, the symmetry of a function is broken by introducing a

multiplier, which increases the intensity on one side from the peak

maximum (usually the low Bragg angle side) and decreases it on the

opposite side. The same modification of intensities can also be achieved

by introducing different peak widths on the opposite sides of the peak

maximum, as has been done in

Figure

2.45.

The following equation

expresses the intensity correction,

as a function of Bragg angle:

Eq.

2.61

is a free variable, i.e. the asymmetry parameter, which is

refined during profile fitting and

is the distance from the maximum of

the symmetric peak to the corresponding point of the peak profile, i.e.

288

20i.

This modification is applied separately to every individual

Bragg peak, including

Ka,

and

Ka2

components. Since Eq.

2.61

is a

simple intensity multiplier, it may be easily incorporated into any of the

peak shape functions considered above. Additionally, in the case of the

Pearson-VII function, asymmetry may be treated differently. It works

nearly identical to Eq.

2.61

and all variables have the same meaning as in

this equation but the expression itself is different:

where

4(2"~

-I), see Eq.

2.52.

Equations

2.61

and

2.62

are quite simple but they are also far from the

best in treating peak asymmetry, especially when high quality powder

diffraction data are available. Better results can be achieved by

introducing the so-called split pseudo-Voigt or split Pearson-VII

functions. Split functions employ two sets of peak shape parameters (all

or only some of them) separately to represent the opposite sides of each

peak. For example, in a split Pearson-VII function, a different exponent

and its dependence on the Bragg angle may be used to model the low

(left) and high (right) angle sides of the peak, while keeping the same

FWHM parameters

and

This results in a total of nine peak shape

184 Chapter

function parameters:

pLo,

and

where

superscripts

and refer to parameters of the left and right sides,

respectively, of the peak (see Eq. 2.52 and following explanation of

notations). It is also possible to split the peak width (FWHM parameters)

but then a total of twelve parameters should be refined, which is usually

an overwhelming number of free variables for an average or even good

quality powder diffi-action experiment.

some advanced implementations of the modified pseudo-Voigt

function, an asymmetric peak can be constructed as a convolution of a

symmetric peak shape and a certain asymmetrization function, which can

be either empirical or based on the real instrumental parameters. For

example, as described in section 2.9.1, and using the Simpson's

multi-

term integration rule this convolution can be approximated using a sum

of several (usually

or 5) symmetric Bragg peak profiles:

where: n is the number of terms, n

or 5;

ysym

and

yasym

are modeled

symmetric and the resulting asymmetric peak shape functions,

respectively, and

are the coefficients describing Bragg angle

dependence of the chosen asymmetry parameter. This approach is

relatively complex but in the case of high accuracy data

(e.g. precision x-

ray or synchrotron powder diffraction), it adequately describes the

observed asymmetry of Bragg peaks. An even more accurate method

employs the modeling of asymmetry by using geometrical parameters

responsible for axial divergence (see section 2.9.1; Finger, Cox, and

Jephcoat reference on page 180). Nevertheless, lower quality routine

powder diffraction patterns to a large extent can be treated using the

simpler

Eq.

2.6 1.

2.10

Intensity of powder diffraction peaks

Any powder diffraction pattern is composed of multiple Bragg peaks,

which have different intensities in addition to varying positions and shapes.

Numerous factors have either central or secondary roles in determining peak

intensities. As briefly mentioned in section 2.7 (Table

2-77,

these factors can

be grouped as: i)

structural factors, which are determined by the crystal

structure; ii)

specimen factors owing to its shape and size, grain size and

distribution, microstructure and other parameters of the sample, and iii)

instrumental factors, such as properties of radiation, type of focusing

geometry, properties of the detector, slit and/or monochromator geometry.

Fundamentals of diffraction

185

The two latter groups of factors may be viewed as secondary, so to say,

they are less critical than the principal part defining the intensities of the

individual diffi-action peaks, which is the structural part.' Structural factors

depend on the internal (or atomic) structure of the crystal, which is described

by relative positions of atoms in the unit cell, their types and other

characteristics, such as thermal motion and population parameters.

this

section, we will consider secondary factors in addition to introducing the

concept of the integrated intensity, while the next section is devoted to the

major component of Bragg peak intensity

the structure factor.

2.10.1

Integrated intensity

Consider the Bragg peak, which is shown in

Figure

2.46,

and let us

try

answer the question: which quantity most adequately describes its intensity,

i.e. what is the combined result of scattering from a series of crystallographic

planes

(hkl)

or, which is the same, from the corresponding point in the

reciprocal lattice? Is it the height of the peak (i.e. the

coordinate of the

highest point)? Is it the area under the peak? Is it something else?

44.00 44.25 44.50 44.75 45.00

Bragg angle,

(deg.)

Figure

2.46.

The relationship between the measured shape (the open circles connected with

the solid lines) and the integrated intensity (shaded area) of the Bragg peak. The background

is shown using the dash-dotted line. The maximum measured intensity is indicated as

Y,,.

The measured intensities and the corresponding values of the background are indicated for

one of the points as

and

bi,

respectively.

Some of the external factors, e.g. preferred orientation (see section

2.10.6),

may have a

tremendous effect on the diffracted intensity. However, all secondary factors have similar

or identical effects on the diffracted intensity, regardless of the crystal (atomic) structure

of the material.

186 Chapter

The value of the peak maximum

(Y,,)

is intuitively and often termed as

its intensity. It can be easily measured and is indeed used in many

applications where relative intensities are compared on a qualitative basis,

e.g. when searching for a similar pattern in a powder diffraction database.

This approach to measuring intensity is, however, unacceptable when

quantitative values are needed because both the instrumental and specimen

factors may cause peak broadening, which may be different for identical

Bragg peaks produced by the same crystalline material. On the other hand,

the area under the peak remains unchanged in most cases, even when

substantial broadening is observed (see Eq.

2.48

indicating that Bragg peak

intensity is a multiplier applied to the corresponding peak shape function,

which has unit area). Thus, the area which is shaded in Figure 2.46 is known

as the integrated intensity, and it represents the true intensity of Bragg peaks

in powder diffraction.

The intensity,

Ihkl, scattered by a reciprocal lattice point (hkl) corresponds

to the integrated intensity of the matching Bragg peak. For simplicity, it is

often called "intensity". What is actually measured in a powder diffraction

experiment is the intensity in different points of the powder pattern and it is

commonly known as profile intensity. Profile intensity is usually labeled

where i is the sequential point number, normally beginning from the first

measured data point (i

1).

Assuming that powder diffraction data were collected with a constant

step in

28,

the area of an individual peak may be calculated simply by

adding the intensities (Y-coordinates) of all points measured within the range

of the peak after the contribution from the background has been subtracted in

every point. The background is shown as a nearly horizontal dash-dotted line

Figure 2.46. The observed integrated intensity (Ihkl) of a Bragg peak

(hkl)

is, therefore, determined from numerical integration as:

I,,

(qobs

b,)

where

is the total number of data points measured within the range of the

peak.'

Strictly speaking, each Bragg peak begins and ends when its contribution becomes

indistinguishable from that of the background. The determination of peak range at its base

presents a challenging numerical problem since i)

diffracted intensity is always

measured with a finite error; ii)

it is nearly impossible to achieve zero background, and

iii)

Bragg peaks often overlap with one another. Thus, for all practical purposes, the

beginning and the end of any Bragg peak (i.e. its width at the base) is usually assumed in

terms of a certain number of full widths at half maximum to the left and to the right from

peak maximum. For Bragg peaks, which are well represented by pure Gaussian

Fundamentals of diffraction

187

The integrated intensity is a function of the atomic structure and it also

depends on multiple factors, such as certain specimen and instrumental

parameters. Considering

Eq.

2.19 and after including necessary details,

earlier grouped as "geometrical" effects, the calculated integrated intensity

in powder diffraction is expressed as the following product:

where:

is the scale factor, i.e. it is a multiplier required to normalize

experimentally observed integrated intensities with absolute calculated

intensities. Absolute calculated intensity is the total intensity scattered by

the content of one unit cell in the direction

(0)

defined by the length of

the corresponding reciprocal lattice vector. Therefore, the scale factor is a

constant for a given phase and it is determined by the number, spatial

distribution and states of the scattering centers (atoms) in the unit cell.

phkl

is the multiplicity factor, i.e. it is a multiplier which accounts for the

presence of multiple symmetrically equivalent points in the reciprocal

lattice.

is Lorentz multiplier, which is defined by the geometry of diffraction.

is the polarization factor, i.e. it is a multiplier, which accounts for a

partial polarization of the scattered electromagnetic wave (see the

footnote and Thomson's equation in section 2.5.1).

is the absorption multiplier, which accounts for absorption of both the

incident and diffracted beams and non-zero porosity of the powdered

specimen.

Thkl

is the preferred orientation factor, i.e. it is a multiplier, which

accounts for possible deviations from a complete randomness in the

distribution of grain orientations.

Ehkl

is the extinction multiplier, which accounts for deviations from the

kinematical diffraction model.

powders, these are quite small and the

extinction factor is nearly always neglected.

Fhkl

is the structure factor (or the structure amplitude), which is defined

by the details of the crystal structure of the material: coordinates and

types of atoms, their distribution among different lattice sites and thermal

motion.

distribution, the number of FWHM's can be limited to

2-3

on each side, while in the case

of nearly Lorentzian distribution this number should be increased substantially (see

Figure

2.42).

In some instances, the number of FWHM's can reach

to 20.

is also possible to

define peak limits in terms of maximum intensity, for example, a peak extends only as far

as profile intensity

(Yi)

remains greater or equal than a certain small predetermined

fraction of the maximum intensity

(Y,,).

188

Chapter

The subscript

hkl

indicates that the multiplier depends on both the length

and direction of the corresponding reciprocal lattice vector

d*hkl.

Conversely,

the subscript

indicates that the corresponding parameter is only a function

of Bragg angle and, thus it only depends upon the length of the

corresponding reciprocal lattice vector,

*hk,.

2.10.2

Scale factor

As described above, the amplitude of the wave (and thus, the intensity,

see Eqs. 2.13 to 2.19 and relevant discussion in section 2.5) scattered in a

specific direction by a crystal lattice is usually calculated for its

symmetrically independent minimum

one unit cell. In order to compare the

experimentally observed and the calculated intensities directly, it is

necessary to measure the absolute value of the scattered intensity. This

necessarily involves

Measuring the absolute intensity of the incident beam exiting through the

slits and reaching the sample.

Precise account of inelastic and incoherent scattering, and absorption by

the sample, sample holder, air and other components of the system, such

as windows of a sample attachment, if any.

Measuring the portion of the diffracted intensity that passes through

receiving slits, monochromator and detector windows.

Correction for efficiency of the detector, number of events generated by a

single photon, detector proportionality, etc, all of which must be precise

and reproducible.

Knowledge of many other factors, such as the volume of the specimen

which participates in scattering of the incident beam, the fraction of the

irradiated volume which is responsible for scattering precisely in the

direction of the receiving slit, and so on.

Obviously, doing all of this is impractical, and in reality the comparison

of the observed and calculated intensities is nearly always done after the

former are normalized with respect to the latter using the so-called scale

factor. As long as all observed intensities are measured under nearly

identical conditions (which is relatively easy to achieve), the scale factor is a

constant for each phase and is applicable to the entire diffraction pattern.

Thus, scattered intensity is conventionally measured using an arbitrary

relative scale and the normalization is usually performed by analyzing all

experimental and calculated intensities using a least squares technique.' The

certain applications, e.g. when the normalized structure factors should be calculated (see

section

2.14.2),

the knowledge of the approximate scale factor is required before the model

of the crystal structure is known. This can be done using various statistical approaches

[e.g. see

A.J.C

Wilson, Determination of absolute from relative x-ray intensity data,

Fundamentals of diffraction

189

scale factor is one of the variables in structure refinement and its correctness

is critical in achieving the best agreement between the calculated and

observed intensities.' Its value is also essential in quantitative analysis of

multiple phase mixtures.

2.10.3

Multiplicity factor

As we established earlier, a powder diffraction pattern is one-dimensional

but the associated reciprocal lattice is three-dimensional. This translates into

scattering from multiple reciprocal lattice vectors at identical Bragg angles.

Consider two points in a reciprocal lattice, 001 and 001. By examining Eqs.

2.29 to 2.34 it is easy to see that in any crystal system lld2(001)

lld2(001).

Thus, Bragg reflections from these two reciprocal lattice points will be

observed at exactly the same Bragg angle.

Now consider the orthorhombic crystal system. Simple analysis of Eq.

2.32 indicates that the following groups of reciprocal lattice points will have

identical reciprocal lattice vector lengths and thus, are equivalent in terms of

the corresponding Bragg angle:

hOO and h00

2 equivalent points

OkO and 0kO

2 equivalent points

001 and 001

2 equivalent points

ha, ha, hkO and

hkO

4 equivalent points

h01, h01, h~land

hoi

equivalent points

Okl, 0x1, 0kland 0kl

- -

- - -

4 equivalent points

hkl, hkl, hkl, hkl, h kl, h kl, h k 1 and h

equivalent points

Assuming that the symmetry of the structure is mmm, these equivalent

reciprocal lattice points have the same intensity in addition to the identical

Bragg angles. Consequently, in general there is no need to calculate intensity

separately for each reflection in a group of equivalents. It is enough to

calculate it for one of the corresponding Bragg peaks and then multiply the

calculated intensity by the number of the equivalents in the group, i.e. by the

multiplicity factor. The multiplicity factor is, therefore, a function of lattice

symmetry and combination of Miller indices.

the example considered

Nature (London)

150,

151 (1942)], consideration of which is beyond the scope of this

book.

The correctness of the scale factor is dependent on many parameters. The most critical are:

the photon flux in the incident beam remains identical during measurements at any Bragg

angle; the volume of the material producing scattered intensity is constant; the number of

crystallites approaches infinity and their orientations are completely random; the

background is accounted precisely; the absorption of x-rays (when relevant) is accounted.

190 Chapter

above (orthorhombic crystal system with point group symmetry mmm), the

following multiplicity factors could be assigned to the following types of

reciprocal lattice points:

phkl= 2 for hOO,

OkO

and 001

phkl= 4 for hkO, Okl and h01, and

phkl=

for hk1

Reciprocal lattices and therefore, diffraction patterns are generally

centrosymmetric regardless of whether the corresponding direct lattices are

centrosymmetric or

---

not. Thus, pairs of reflections with the opposite signs of

indices, (hkZ) and (h k

the so-called Friedel pairs

usually have equal

intensity. Yet, they may be different in the presence of atoms that scatter

anomalously (see section 2.11.4) and this phenomenon should be taken into

account when multiplicity factors are evaluated comprehensively. Relevant

details associated with the effects of anomalous scattering on the multiplicity

factor will be considered below in section 2.12.2.

2.10.4

Lorentz-polarization factor

The Lorentz factor takes into account two different geometrical effects

and it has two components. The first is owing to finite size of reciprocal

lattice points and finite thickness of the Ewald's sphere, and the second is

due to variable radii of the Debye rings. Both components are functions of 8.

Usually the first component is derived by considering a reciprocal lattice

rotating at a constant angular velocity around its origin. Under these

conditions, various reciprocal lattice points spend different time in contact

with the surface of the Ewald's sphere. Shorter reciprocal lattice vectors are

in contact with the sphere for longer periods when compared with longer

vectors.

powder diffraction, this contribution arises from the varying

density of the equivalent reciprocal lattice points resting on the surface of the

Ewald's sphere, which is a function of

d*.

It can be shown that the first

component of the Lorentz factor is proportional to lIsin9.

The second component accounts for a constant length of the receiving

slit. As a result, a fixed length of the

Debye ring is always intercepted by the

slit regardless of Bragg angle. The radius of the ring (rD) is, however,

proportional to sin28.l Because the scattered intensity is distributed evenly

along the circumference of the ring, the intensity that reaches the detectors

becomes inversely proportional to r~ and, therefore, directly proportional to

1 lsin28.

This proportionality holds as long as the distance between the specimen and the receiving

slit of the detector remains constant at any Bragg angle.