Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffraction

Yet another level of complexity of vibrational motion is taken into

account by using the so-called anharmonic approximation of atomic

displacement parameters. One of the commonly used approaches is the

cumulant expansion formalism suggested by Johnson,' in which the structure

factor is given by the following general expression:

F(h)

&fJ

(s) exp(2trih

Pll

h, h,

j=1

where

PJkl

are the anisotropic displacement parameters (see Eq. 2.93);2

yJklm are the third order anharmonic displacement parameters;

8Jklmn are the fourth order displacement parameters. The expansion in Eq.

2.98 may be continued to include fifth, sixth, and so on order terms. The

sign of the corresponding term is determined from the sign of

where

is the order of the anharmonic term;

k, 1, m, n (p, q, etc., in the higher order expansions) vary between

and

hk, hl, h, and h, (h,, h,, etc.) are the corresponding Miller indices (hl

and h3

respectively);

other notations are identical to

Eq.

2.87.

Displacement parameters are included in

Eq.

2.97 with all possible

permutations of indices. Thus, for a conventional anisotropic approximation

after considering the diagonal symmetry of the corresponding tensor (Eq.

2.96)

the already known expression for the exponential factor in Eq. 2.93 is easily

obtained. Following the same procedure it is possible to show that in the

case of the third order anharmonic expansion the number of the independent

C.K.

Johnson, in: Thermal neutron diffraction: proceedings of the International Summer

School at Harwell, 1-5 July 1968 on the accurate determination of neutron

intensities and structure factors, p. 132-160,

B.T.M.

Willis, Ed., London, Oxford

University Press (1970).

In this treatment, the conventional harmonic anisotropic displacement model may be

considered as a "second order" approximation.

212

Chapter

atomic displacement parameters is increased by 10 (yl

yzz2, y333, y1 12, y113,

Y~zz, 7133, y221, y223,

Y233

and y123).' Similarly, the maximum number of

parameters per atom in the fourth order expansion is increased by 1 5 (a1

62222, 83333, 61112, 61113, 61122, 61133, 81123, 61222, 61223, 61233, 61333, 62223, 62233

and 62333), fifth order by

1, and so on.

A brief description of the anharmonic approximation is included here for

completeness since rarely, if ever, it is possible to obtain reasonable atomic

displacement parameters of this complexity from powder diffraction data:

the total number of atomic displacement parameters of an atom in the fourth

order anharmonic approximation may reach 31

anisotropic

10 third

order

15 fourth order). The major culprits preventing their determination in

powder diffraction are uncertainty of the description of Bragg peak shapes,

non-ideal models to account for the presence of preferred orientation, and

the inadequacy of accounting for porosity.

2.1

1.4

Atomic scattering factor

As briefly mentioned above (see section 2.5.2), the ability to scatter

radiation varies depending on the type of an atom and therefore, the general

expression of the structure amplitude contains this factor as a multiplier

(Eq.

2.87). For x-rays, the scattering power of various atoms and ions is

proportional to the number of core electrons. Therefore, it is measured using

a relative scale normalized to the scattering ability of an isolated electron.

The x-ray scattering factors depend on the radial distribution of the electron

density around the nucleus and they are also functions of Bragg angle.

When neutrons are of concern, their coherent scattering by nuclei is

independent of the Bragg angle and the corresponding factors remain

constant for any Bragg reflection. Scattering factors of different isotopes are

represented in terms of coherent scattering lengths of a neutron and are

expressed in femtometers (1 fm

lo-'' m).

The best known scattering factors for x-rays and scattering lengths for

neutrons of all chemical elements are listed for common isotopes and their

naturally occurring mixtures (neutrons) and for neutral atoms and common

ions (x-rays) in the International Tables for

Crystall~graphy.~

Just as in the case of the conventional anisotropic approximation, the maximum number of

displacement parameters is only realized for atoms located in the general site position (site

symmetry 1). In special positions some or all of the displacement parameters will be

constrained by symmetry. For example,

y3,,, yl13,

y223

and

y12,

for an atom located in the

mirror plane perpendicular to Z-axis are constrained to

Furthermore, if an atom is

located in the center of inversion, all parameters of the odd order anharmonic tensors

(3,

etc.) are reduced to

International Tables for Crystallography, vol. C,

2nd

edition, A.J.C. Wilson and

Prince,

Eds., Second edition, Kluwer Academic Publishers, Boston/Dordrecht/London (1 999).

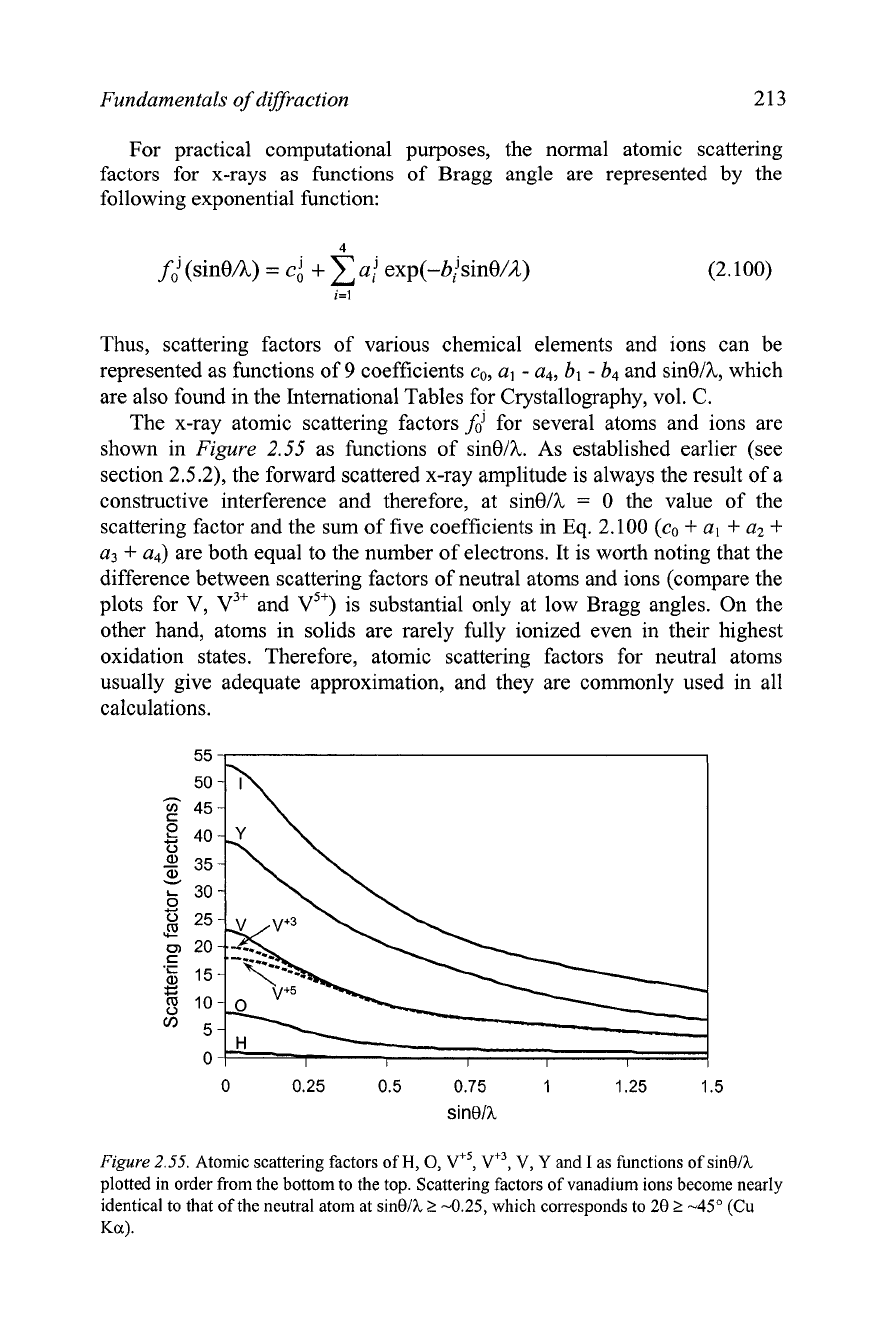
Fundamentals of diffraction 213

For practical computational purposes, the normal atomic scattering

factors

for x-rays as functions of Bragg angle are represented by the

following exponential function:

Thus, scattering factors of various chemical elements and ions can be

represented as functions of

coefficients

co,

a4, bl

b4 and sinelh, which

are also found in the International Tables for Crystallography, vol.

The x-ray atomic scattering factors

for several atoms and ions are

shown in Figure

2.55

as functions of sinelh. As established earlier (see

section 2.5.2), the forward scattered x-ray amplitude is always the result of a

constructive interference and therefore, at sinell,

0 the value of the

scattering factor and the sum of five coefficients in Eq. 2.100 (co

a4) are both equal to the number of electrons. It is worth noting that the

difference between scattering factors of neutral atoms and ions (compare the

plots for V,

v3+

and v5+) is substantial only at low Bragg angles. On the

other hand, atoms in solids are rarely fully ionized even in their highest

oxidation states. Therefore, atomic scattering factors for neutral atoms

usually give adequate approximation, and they are commonly used in all

calculations.

Figure

2.55.

Atomic scattering factors of

vf5,

v+~,

and

as functions of sin01h

plotted in order from the bottom to the top. Scattering factors of vanadium ions become nearly

identical to that of the neutral atom at

sinO/h

-0.25, which corresponds to

-45"

(Cu

Ka)

214

Chapter

Considering

Figure

2.53 and

Figure

2.55, both the temperature and

scattering factors decrease exponentially with sin01A. Hence, when the

displacement parameter of an individual atom becomes unphysical during a

least squares refinement, this usually means that the improper type of an

atom has been placed in the suspicious site. If the chemical element placed

in a certain position has fewer electrons than it should, then during the

refinement its displacement

parameter(s) becomes negative or much lower

than those of the correctly placed atoms. This reduction in the displacement

parameters(s) (Eq. 2.91 to 2.95) offsets the inadequately low scattering

factor (Eq. 2.100) by increasing the temperature factor. Similarly, when the

site has too many electrons than it really does, displacement parameter(s) of

the corresponding atom will be unusually high during the refinement.

Similar effects are observed in neutron diffraction.

Anomalous displacement

parameter(s) will be also observed when an

atom is placed in a position that is empty or only partially occupied

(i.e. the

site has sizeable defects).

this case, displacement parameter(s) become

extremely large, effectively reducing the contribution from this atom to the

structure factor (see

Figure

2.53). All sites, which have unusually low or

unusually high displacement parameter(s), should be tested by refining

population

parameter(s), while setting the displacement parameters at some

reasonable values to avoid possible and sometimes severe correlations. This

refinement may reveal the nature of the chemical element located in a

specific position by analyzing the number of electrons (or scattering length

in neutron diffraction).

For example, assume that a Ni atom has been placed in a certain position

and a least squares refinement results in a large and positive isotropic

displacement parameter for this site but displacement parameters of other

atoms are in the "normal" range. After the population parameter of Ni has

been refined while keeping its displacement parameter fixed at the average

value of other "normal" atoms, the resulting

gNi

0.5. Considering

Figure

Ni Ni

2.55, the approximate number of electrons in this position is equal to

28~0.5

Hence, the refinement result points to one of the following: i)

the site is occupied by Ni atoms at 50

population (50

of the unit cells

have Ni in this position and in the remaining 50

the same position is

vacant), or ii) the site is occupied by the element that has approximately 14

electrons,

i.e. Si. Depending on many other factors (e.g. precision of the

experiment) the same position may be also occupied by

(13

electrons),

electrons) or by other neighboring atoms.

The final decision about the population of this "Ni" site can be made only

when all available data about the material are carefully considered: i) which

chemical elements may be present in this sample or were used during its

preparation, if known? ii) what are the results of the chemical analysis? iii)

Fundamentals of diffraction 215

what is the gravimetric density of the material? and iv) what is the

environment of this particular position? For example, an octahedral

coordination usually points to

A1 but not Si or

It should be emphasized that the calculation of the number of electrons

described above is not exact since x-ray scattering factors are only directly

proportional to the number of electrons at 20

0" and the proportionality

becomes approximate at sinelk

0. The population parameter(s) refinement

results are usually more reliable in neutron diffraction because neutron

scattering lengths are independent of the Bragg angle.

Normal x-ray scattering factor,

(Eq.

2.100) describes the scattering

ability of different atoms as a function of sinell. (or interplanar distance, d,

since

sinelk

112d) and, therefore, is wavelength independent. This is only

true for light chemical elements and relatively short wavelengths. Most

atoms scatter x-rays anomalously and their scattering factors become

functions of the wavelength.' Anomalous scattering is taken into account by

including two additional parameters into the overall scattering factor of each

chemical element in the following form:

where:

is sinelk;

fbj

is the normal atomic scattering factor that depends only on the type of

the scattering atom (number of electrons) and is a function of sine/h;

~fj'

and

j''

are the real and imaginary components, respectively, of the

anomalous scattering factor and they depend on both the atom type and

the wavelength.

The anomalous scattering coefficients are also listed in the International

Tables for Crystallography for all chemical elements and commonly used

wavelengths of laboratory x-rays. They can be measured or calculated for

any wavelength, which is important when using synchrotron

radiati~n.~ The

anomalous scattering is usually at least an order of magnitude lower than

normal scattering. Generally, the magnitude of the anomalous scattering

coefficients is proportional to the wavelength and inversely proportional to

the number of electrons in an atom. Anomalous scattering is at its maximum

when the wavelength is near the corresponding absorption edge of an atom.

Some isotopes also scatter neutrons anomalously.

The most precise values are obtained from experimental measurements. When one of the

two anomalous scattering coefficients is measured, the second can be relatively precisely

calculated using Kramers

Kronig equation. More details about the anomalous scattering

can be found in a special literature, e.g. see

Als-Nielsen and

McMorrow, Elements of

modern x-ray physics, John Wiley

Sons, Ltd., New York

(2001).

216

Chapter

2.11.5

Phase

angle

The structure amplitude, expressed earlier as a sum of exponents, can be

also represented in a different format. Thus, by applying Euler's formula

cosx

isinx

(2.102)

Eq. 2.89 becomes

The sums of cosines and sines in Eq. 2.103 signify the real (A) and

imaginary (B) components of a complex number, respectively, which the

structure amplitude indeed is. Hence, considering the notations introduced in

Eq. 2.87, Eq. 2.103 can be rewritten as:

Complex numbers can be represented as vectors in two dimensions with

two mutually perpendicular axes: real and imaginary. Accordingly, the

complex structure amplitude (Eq. 2.104) may be imagined as a vector

and

its real and imaginary components are the projections of this vector on the

real and imaginary axes, respectively, as shown schematically in

Figure

2.56,

left. From simple geometry, the following relationships are true:

where IF(h)l, IA(h)l and IB(h)l are the lengths of the corresponding vectors

(or their absolute values), and a(h) is the angle that vector F(h) makes with

the positive direction of the real axis, also known as the phase angle (or the

phase) of the structure amplitude. It is worth noting that since

A(h) and B(h)

are mutually perpendicular, the phase shift between the imaginary and real

components of the structure amplitude is always +n/2.

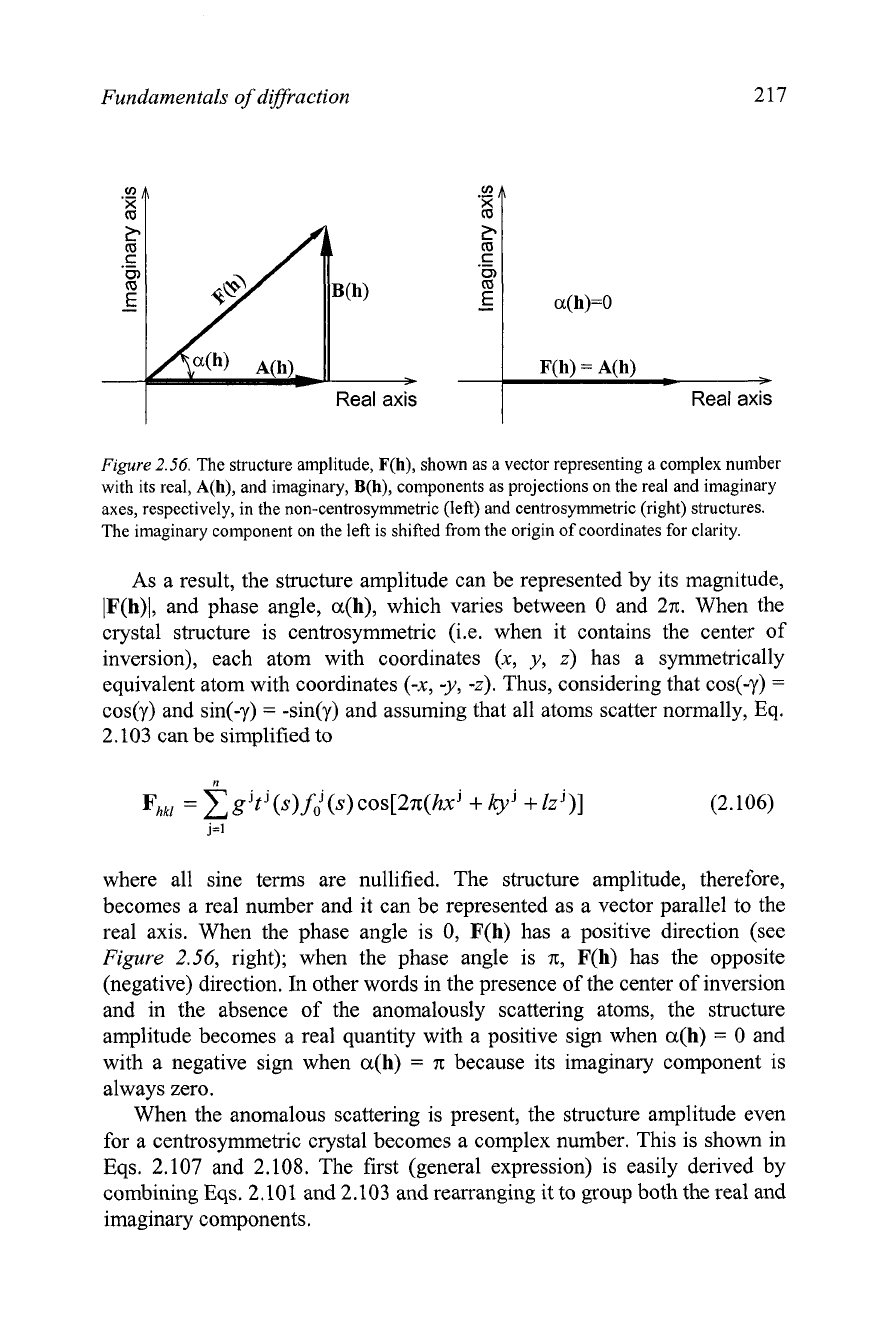
Fundamentals

diffraction

Real axis

Figure

2.56.

The structure amplitude, F(h), shown as a vector representing a complex number

with its real, A(h), and imaginary,

B(h),

components as projections on the real and imaginary

axes, respectively, in the non-cenhosyrnmetric (left) and centrosymrnetric (right) structures.

The imaginary component on the left is shifted from the origin of coordinates for clarity.

As a result, the structure amplitude can be represented by its magnitude,

IF(h)l, and phase angle, a(h), which varies between 0 and 2n. When the

crystal structure is centrosymmetric (i.e. when it contains the center of

inversion), each atom with coordinates (x, y,

has a symmetrically

equivalent atom with coordinates (-x, -y,

-z).

Thus, considering that cos(-y)

cos(y) and sin(-y)

-sin(y) and assuming that all atoms scatter normally, Eq.

2.103 can be simplified to

where all sine terms are nullified. The structure amplitude, therefore,

becomes a real number and it can be represented as a vector parallel to the

real axis. When the phase angle is 0, F(h) has a positive direction (see

Figure

2.56,

right); when the phase angle is n, F(h) has the opposite

(negative) direction.

other words in the presence of the center of inversion

and in the absence of the anomalously scattering atoms, the structure

amplitude becomes a real quantity with a positive sign when a(h)

0 and

with a negative sign when a(h)

because its imaginary component is

always zero.

When the anomalous scattering is present, the structure amplitude even

for a centrosymmetric crystal becomes a complex number. This is shown in

Eqs. 2.107 and 2.108. The first (general expression) is easily derived by

combining Eqs. 2.10 1 and 2.10

and rearranging it to group both the real and

imaginary components.

g't

(s)

~fi

(s)

cos[2n(hxJ

kyj

lzj)]

j=1

(2.107)

g't' (s)

~f,'

(s)

sin[2n(hx'

)]

Zg'tJ (s)Af

"cos[2n(hx'

kyJ

lzJ)]

j=1

Chapter

The introduction of the center of inversion results in the cancellation of

all sine terms in Eq. 2.107 and

Recalling that usually

<<fdj

'I, the absolute value of the imaginary

component in Eq. 2.108 is smaller than that of the real part, and phase angles

remain close to

0 or

in any centrosymmetric structure.

the

non-

centrosymmetric cases (Eq. 2.107) the phase angles may adopt any value

between 0 and 2n.

conclusion of this section, it is worth noting that the measured

integrated intensity (Eq. 2.65) is proportional to the square of the structure

amplitude. Thus, the relative absolute value of the structure amplitude is an

easily measurable quantity

it can be obtained as a square root of intensity

after dividing the latter by all known geometrical factors. The phase angle

(or the sign in case of normally scattering centrosymmetric structures),

however, remains unknown.

other words, phases are lost and cannot be

determined directly from either a powder or a single crystal diffraction

experiment. This creates the so called "phase problem" in diffraction

analysis, and its significance will be discussed later in this Chapter (see

section 2.14).

2.12

Effects of symmetry on the structure amplitude

Considering the most general expression of the structure amplitude, Eq.

2.107, its value is defined by population and displacement parameters of all

Fundamentals of diffraction

219

atoms present in the unit cell, their scattering ability and coordinates. We

know that coordinates and other parameters of atoms in the unit cell are

related by symmetry. As was shown in Chapter 1 (Eqs. 1.39 and

1.48), the

coordinates of two symmetrically equivalent atoms (x and xl) are related as

where

(x,

z, 1) x'

(x',

y',

z', 1) and

is an augmented matrix

representing a symmetry operation. By expanding Eq. 2.109, substituting the

result to express the identical arguments of sine and cosine parts in Eq. 2.107

and regrouping it as shown in Eq. 2.1 10

27th.

x'=

27t

~(~~11

k~l

+Ir31)

~(~~12

kr22

+Ir,,)

(2.1 10)

z(hr13

Ir3,)

(ht,

kt2 +It3)

it is easy to see that the symmetry of the direct space (crystal structure) is

carried over into the reciprocal space by modifying structure amplitudes.

Thus, the contribution of two symmetrically equivalent atoms

and x' into

the corresponding reciprocal lattice points, h and h', may be expressed as

where

and

are augmented reciprocal lattice vectors, and

is obtained

from

by transposing the rotational part of the augmented matrix:

and

As a result of symmetry transformation (Eqs. 2.1 11 and 2.1 12), both the

magnitude of the structure amplitude and its phase may change. Finite

symmetry operations

(tl, t2

and

are all 0) usually affect the phase angle,

while infinite operations, i.e. those which have a non-zero translational

component, affect both the magnitude and the phase.

2.12.1

Friedel pairs and Friedel's law

We begin with considering the relationships between the structure

amplitudes of two centrosyrnmetric reciprocal lattice points: (hkl) and (h kl),

220

Chapter

the so-called Friedel pair. The analysis is relatively simple and is based on

the known relationships between the three trigonometric functions:

cos(-x)

cos(x),

but

(2.1 13)

sin(-x)

sin(x) and tan(-x)

tan(x)

Regardless of whether the crystal structure is centrosymmetric or not, in

the absence of the anomalous scattering it directly follows from Eqs. 2.103,

2.104, 2.105 and2.113 that

Equation 2.1 14 represents the algebraic formulation of the Friedel's law,

which states that the absolute values of structure amplitudes and intensities

are identical but the phase angles have opposite signs for Bragg reflections

related to one another by the center of inversion.

another formulation, it

states that the reciprocal space is always centrosymmetric in the absence of

the anomalous scattering because IF(h)l

lF(h)l. Friedel's law is illustrated

Figure

2.57,

left.

On the contrary, when the anomalous scattering is substantial, then

considering Eq. 2.107 instead of Eq. 2.103, both the real and imaginary

components of the structure amplitude are modified as follows

A(h)

6A" (h)

~(h)

A(h)

6A" (h)

B(h)

(h)

~(h)

-B(h)

6B" (h)