Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Fundamentals

of

diffraction

23

1

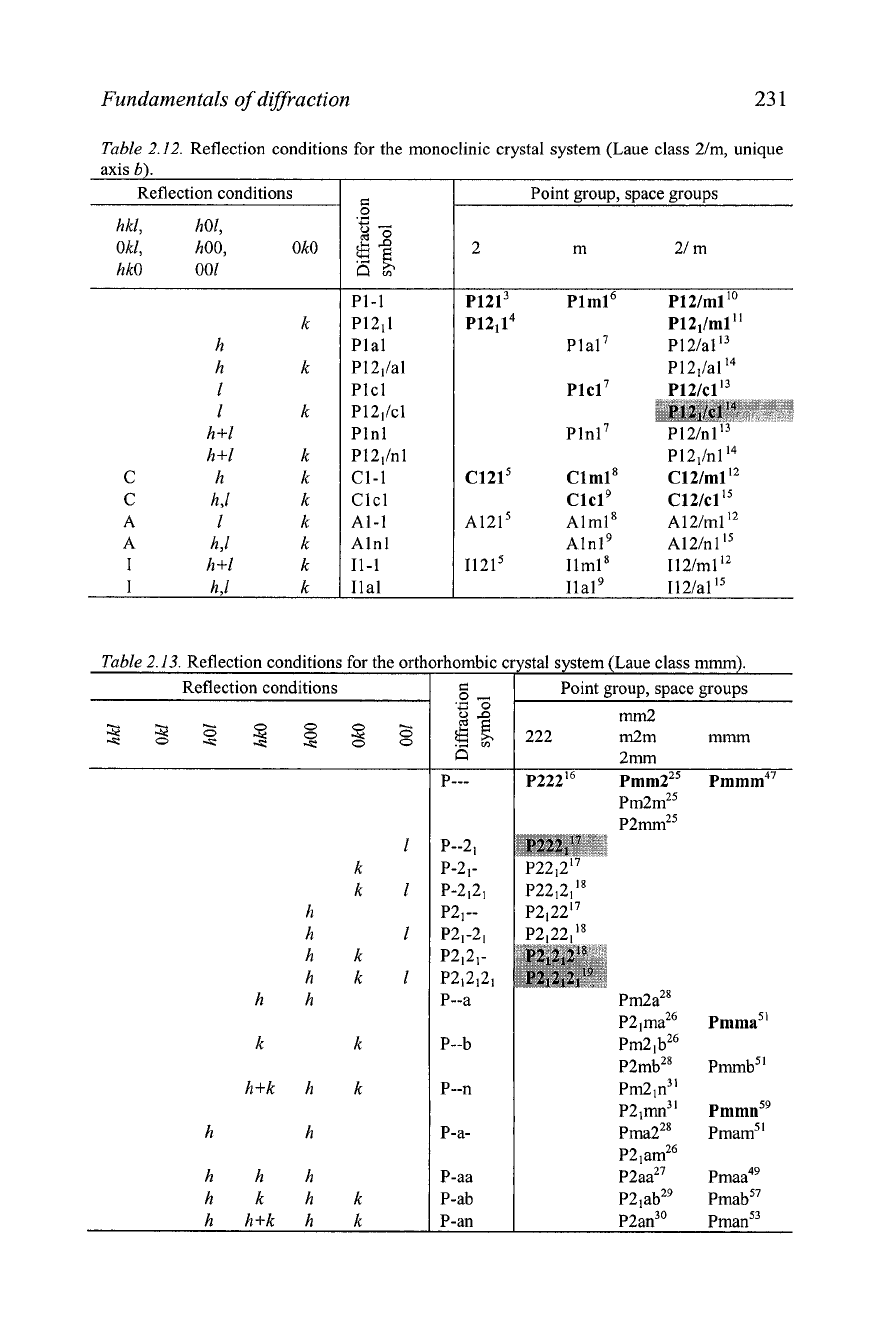
Table

2.12.

Reflection conditions for the monoclinic crystal system (Laue class 2/m, unique

axis

b).

Reflection conditions

hkl, h01,

Okl, hOO, OkO

hkO 001

8

'C

2

5

'I

n

v,

PI-l

PI211

Plal

P12,Ial

Plcl

P12'/~l

Plnl

P121/nl

CI-l

Clcl

Al-l

Alnl

11-1

Ilal

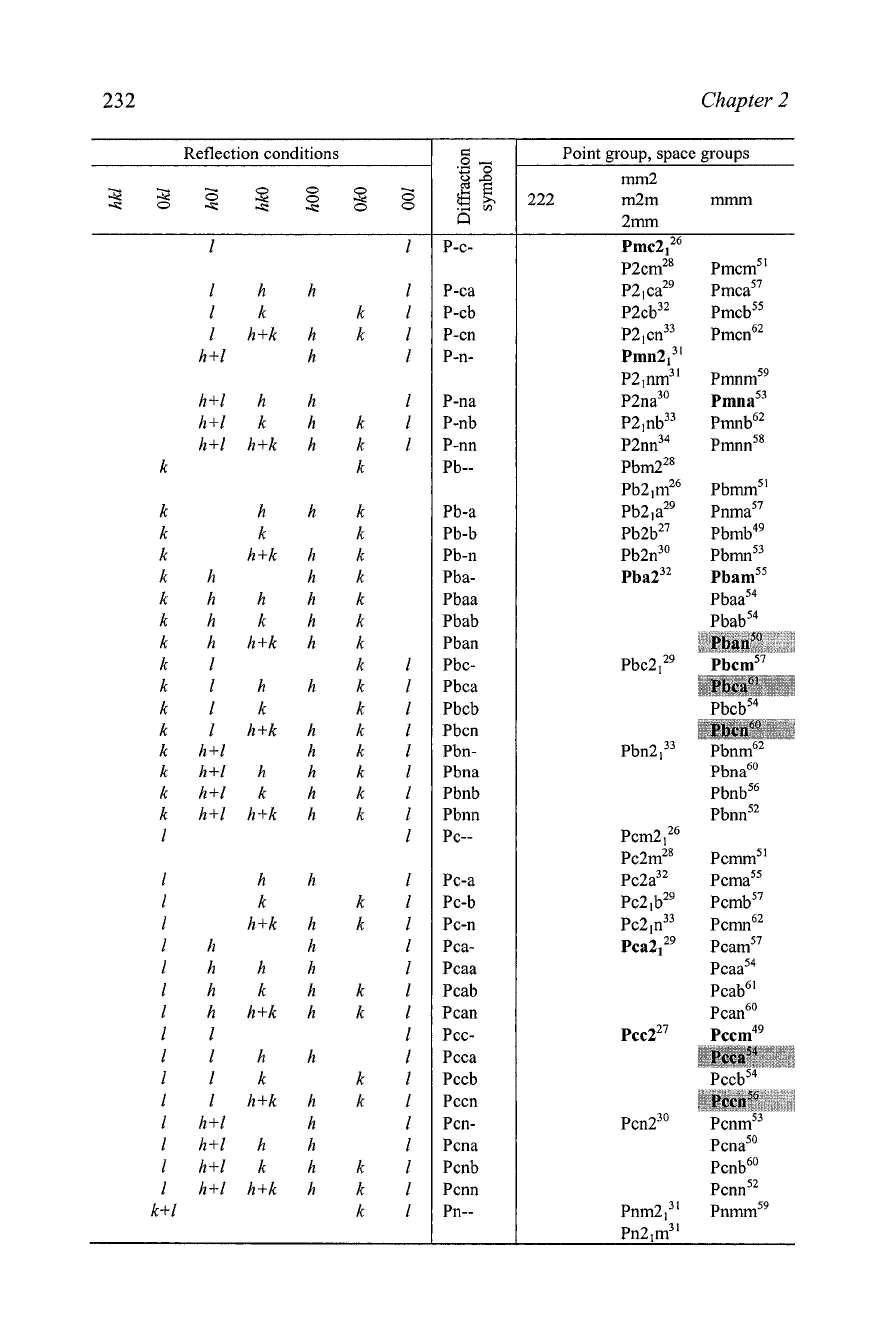
Table

2.13.

Reflection conditions for the ortl

Reflection conditions

h

hh

k

h+k h

h h

hhh

hkh

Point group, space groups

rhombic

G

.o"

s

a

P--21

P-2'-

P-2'2'

P2'--

P2'-2'

P2'2,-

p212121

P--a

P--b

P--n

P-a-

P-aa

P-ab

P-an

Point group, space groups

232

Chapter 2

Reflection conditions

C

lhh

1

k k

1

h+k h k

1

h+l h

1

k hhk

k k k

k h+k h k

kh hk

khhhk

khkhk

k h h+k h k

k

1

k

1

klhhkl

klk k

1

k lh+kh k

1

k h+l hkl

kh+lh h k

1

kh+lk

h

k

I

k h+l h+k h k

1

1 1

1

hh

1

k k

1

h+k h k

1

1 h h

1

lhhh

1

lhkhkl

1

hh+kh k

1

11

1

llhh

1

Ilk k

1

lh+kh k

1

h+l h

1

h+l h h

1

lh+lk h k

1

h+l h+k h k

1

k+l k

1

P-c-

P-ca

P-cb

P-cn

P-n-

Pb-a

Pb-b

Pb-n

Pba-

Pbaa

Pbab

Pban

Pbc-

Pbca

Pbcb

Pbcn

Pbn-

Pbna

Pbnb

Pbnn

PC--

PC-a

PC-b

PC-n

Pca-

Pcaa

Pcab

Pcan

Pcc-

Pcca

Pccb

Pccn

Pcn-

Pcna

Pcnb

Pcnn

Pn--

Point group, space groups

mrn2

222

m2m

mmm

2mm

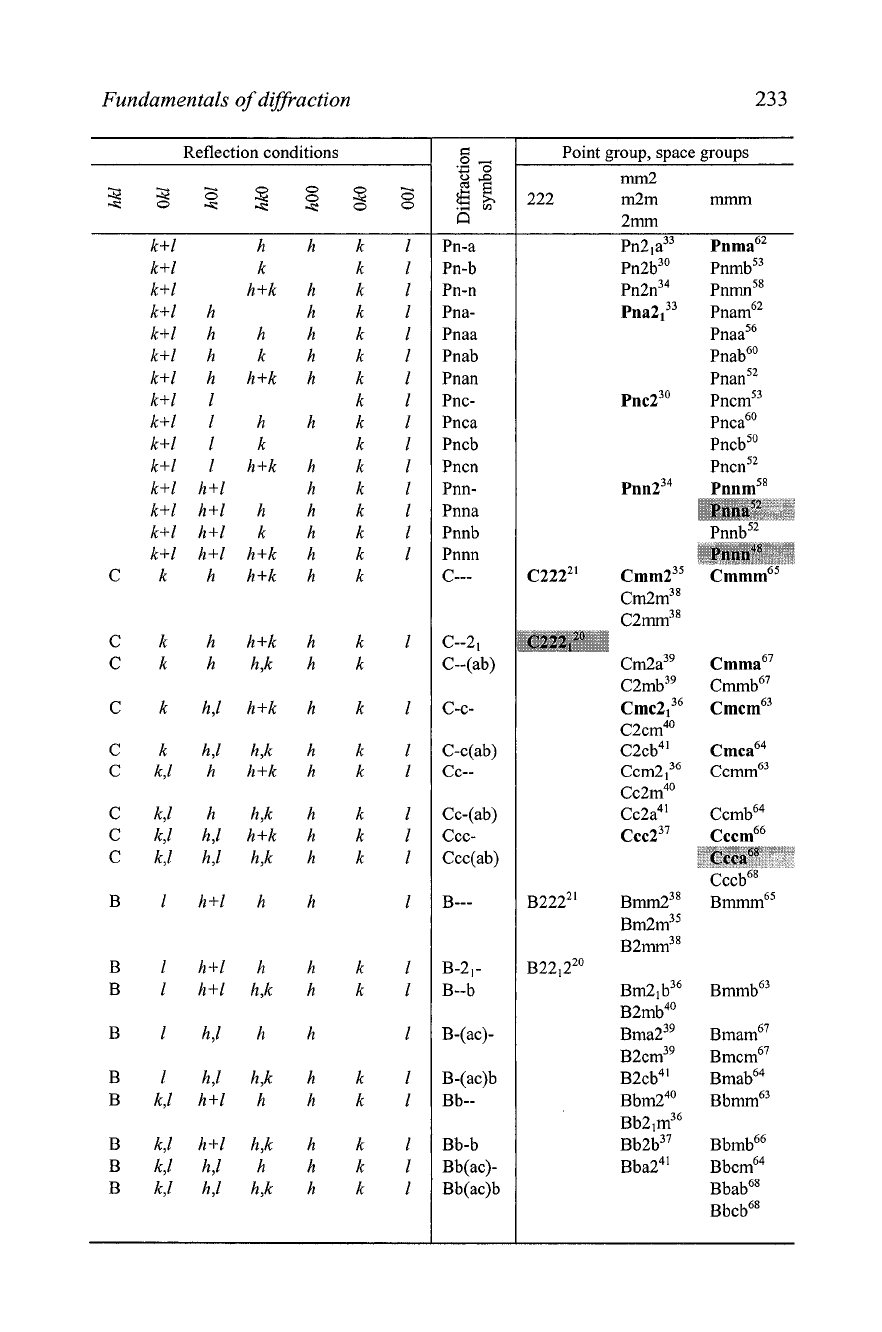
Fundamentals of diffraction

233

Reflection conditions

I

Point group, space groups

2mm

k+l hhkl

k+l k k

1

k+l h+k h

k

1

k+l h hkl

k+lh h h k

1

k+lh k h k

1

k+l h h+k h k

1

k+l

1

k

1

k+l

1

h

k

1

k+l

1

k k

1

k+l

1

h+k h k

1

k+l h+l hkl

k+l h+l h h k

1

k+l h+l k h k

I

k+l h+l h+k h k

1

k h h+k h k

Pn-a

Pn-b

Pn-n

Pna-

Pnaa

Pnab

Pnan

Pnc-

Pnca

Pncb

Pncn

Pnn-

Pnna

Pnnb

Pnnn

c---

~222~' ~mm2~~ Cmmm

~m2rn~~

C-c-

Cc-(ab)

Ccc-

Ccc(ab)

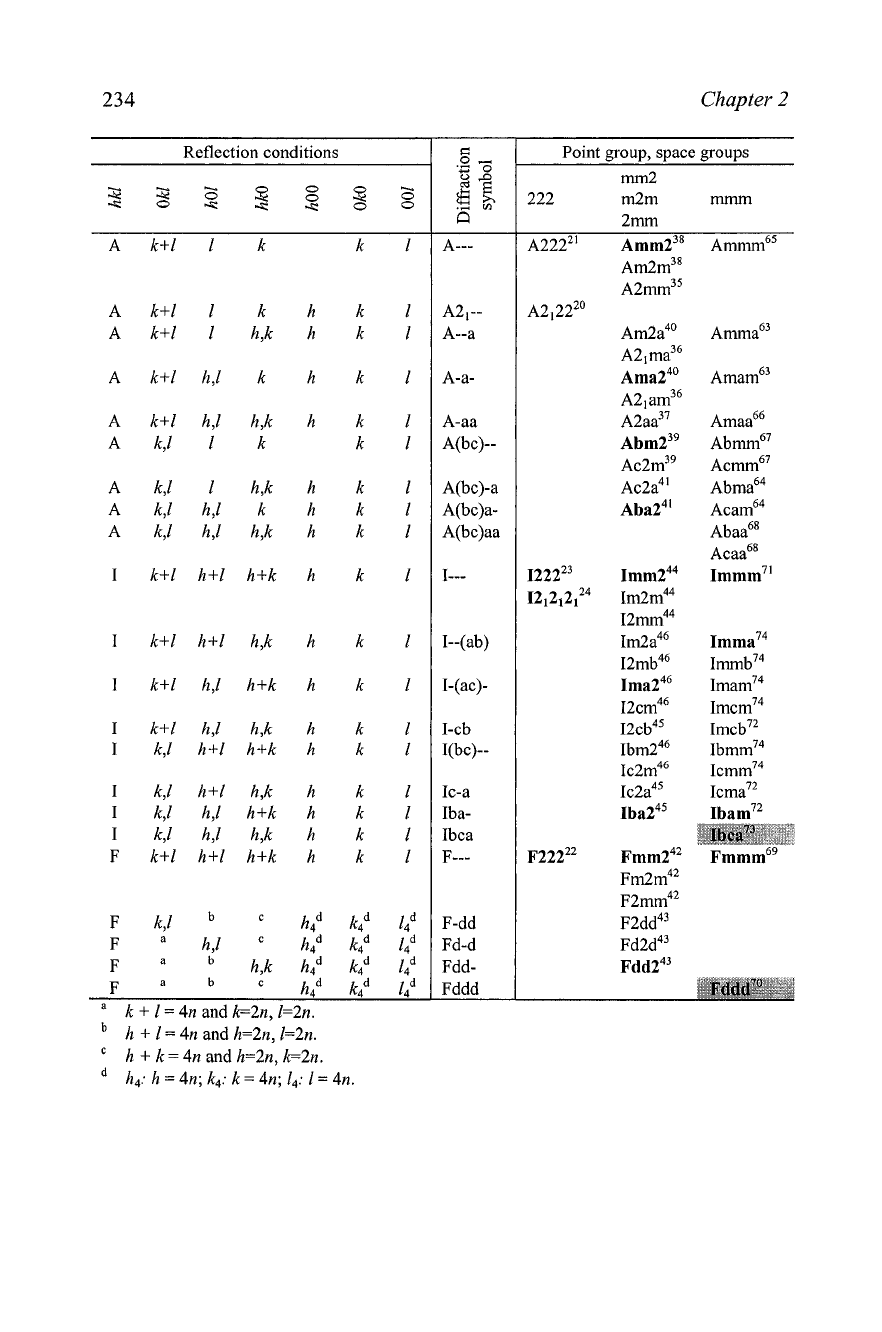
234

Chapter

2

1

hqd kqd

$

i-dd

a

h,l hqd kqd

Fd-d

a

h,k hqd kqd lqd

~dd-

F

a

hqd kqd

1:

Fddd

a

k

+

1

=

4n and k=2n, 1=2n.

h

+

1

=

4n and h=2n, 1=2n.

h

+

k

=

4n and h=2n, k=2n.

h4:

h

=

4n; k4:

k

=

4n;

14: 1

=

4n.

I

k,l

h+l

h,k h k

1

I

k,l

h,l h+k h k

1

I

k,l

h,l

h,k h k

1

F

k+l h+l

h+k

h

k

1

Point group, space groups

mrn2

222 m2m

rnmrn

2mm

I

~222~' ~rnrn2~~ Amrnd5

~m2rn~~

~2mm~~

~2~22"

Am2a40 ~rnrna~~

~2~ma~~

~rna2~' ~mam~~

~2,arn~~

~2aa~~

~brn2~~ ~bmm~~

~c2rn~~ ~cmm~~

Ac2a4' ~bma~~

~ba2~'

cam^^

Abaa6*

Acaa6'

1222'~ 1rnrn2~~ 1rnrnrn7'

12~2~2~~~ 1m2m~~

12mm~~

1m2a~~ ~rnrna~~

12~b~~ ~~b~~

1rna2~~

12cm~~ ~mcrn'~

12cb~~ 1mcb7'

1brn2~~ ~bmm~~

1c2rn~~ ~cmrn~~

1c2a~~ ~cma~~

1ba2~' 1barn7'

~222~' ~rnrn2~~

~m2m~~

~2rnm~~

~2dd~~

~d2d~~

Ic-a

Iba-

Ibca

F---

Fundamentals of diffraction

235

Table

2.14.

Reflection conditions for the trigonal crystal system. There are no space groups

with a unique set

(

Reflection

conditions

reflection conditions.

I

R

b,l 13~

12

I

a

These diffraction groups have

r

-

:

groups

-

312 31m 31m

~3 12'~~ ~3 lmIs7 ~31m'~~

:

same reflection conditions as the following hexagonal

3,

3

I

C

0

3

.

-

4-

0

i5

*

-.

:h<

- -

groups:

P---,

P62--, P--c, and P-c-. Therefore, they are indistinguishable from systematic

absences using powder data.

~en~is-h+k+1=3n,thenh+l=3n;when~ish-k+l=3n,then-h+1=3n.

13:

1

=

3n; 16: 1

=

6n.

Laue Class

Table

2.15.

Reflection conditions for the hexagonal crystal system. There are no space groups

- -

3

I

3ml

with a unique set of ref

-

31m

Reflection

conditions

Point group, spact

ction cc

c

,s

z

P

@

8

n

p---a

P63

P62--a

P6!--

P--ca

P-c-~

P-cc

Laue Class

t group, space groups

622,6mm 62m, 6m2 6lmmm

P~cc'~~

~61mcc'~~

a

These diffraction groups have the same reflection conditions as the following trigonal

groups: P---, P3'--, P--c, and P-c-. Therefore, they are indistinguishable from systematic

absences using powder data.

13: 1

=

3n;

4:

1

=

6n.

Chapter

2

Table

2.16.

Reflection condi

Reflection conditions

I

h+k k+l

1 1:

k

I

h+k k+l lqa k

I

h+k k,l

11

k

I

h+k k,l

1:

k

I

h,k k+l

1 1:

k

I

h,k k+l

L"

k

)---

'-2'-

'42--

'422'-

'4'--

'4121-

LC

'-2'c

3-b-

'-bc

LC-

='-cc

?-n-

?-nc

Pn--

P42/n--

Pn-c

Pnb-

Pnbc

Pnc-

Pncc

Pnn-

Pnnc

[---

I4'--

I--d

I-c-

I-cd

14'/a--

Ia-d

Iacd

tetragonal crystal system.

Laue Class

4lm 4/mmm

Point group, space groups

Fundamentals

of

diffraction

237

Table

2.17.

Reflection cc

Reflection

conditions

F

d,

k,l h,l lda

a

la:

1

=

4n.

ditions

e

0-

.;

0

0s

4

g

8

p---

p2

1

p42

p4

1

P--n

Pa--

Pn--

Pn-n

I---

I4,--

I--d

Ia--

Ia-d

F---

F4

--

F--C

Fd--

Fd-c

Point group

-

23 m3

1

432 43m m3m

r the cubic crystal system.

Laue Class

Conditions are for

Okl: k

=

2n; for

h01:

1

=

2n; for

hkO:

h

=

2n.

'

2h+l=4n.

2k+l=4n.

m7

2.13

Fourier transformation

m3m

In

crystallography, direct and reciprocal spaces are related to one another

as forward and reverse Fourier transformations.

In

three dimensions these

relationships can be represented by the following Fourier integrals:

23 8

Chapter 2

where Eq. 2.129 is forward (-i) and Eq. 2.128 is reverse (+i) Fourier

transforms. Here, @(h) is the function defined in the reciprocal space, i.e. the

scattered amplitude; p(x) is the corresponding function defined in the direct

space, e.g. p(x) is the electron density when scattering of x-rays is of

concern or it is the nuclear density when scattering of neutrons on nuclei is

considered; h and x are the coordinate vectors in the reciprocal and direct

spaces, respectively;

V*

and

V

are, respectively, reciprocal and direct space

volumes, and

i

=

fi

.

Both integrals do not require assumption of periodicity and they can be

used to calculate the scattered amplitude or the corresponding density

function of any direct or reciprocal object, respectively. For example, Eq.

2.128 results in the atomic scattering factor,

flsinelh)

cc

I@(h)l, when the

integration is performed for an isolated atom.

In

this case, p(x) is the

electron density distribution in the atom, which is usually obtained from

quantum mechanics.

Considering a crystal, in which the electron density function is periodic,

the integral in Eq. 2.128 can be substituted by a sum:

F(h)

=

v

p(x)

exp[2ni(h

.

x)]

X

where P(h) is the structure amplitude at a reciprocal lattice point h,

V

is the

volume of the unit cell of the direct lattice and the summation is carried over

all possible coordinate vectors, x, in the unit cell for a specific h.

When Eq. 2.130 is compared with Eq. 2.87, it is easy to see that the

distribution of the electron density in the unit cell is modeled by

n products,

g'P(sinelhlfJ(sinelh), where

g',

P

and

f

j

are the population, temperature and

scattering factors of the

jth

atom, respectively, and the summation ranges

over all atoms (from 1 to n) that are present in the unit cell.

Similar substitution of the forward Fourier integral (Eq. 2.129) results in

the following sum, which enables one to calculate the distribution of the

electron (or nuclear) density in the unit cell from the known structure

amplitudes:

1

p(x)

=

-

~(h) exp[- 2ni(h

.

x)]

v

h

Here the summation is carried over all reciprocal lattice points, h, for a

given coordinate vector,

x.

The last equation has exceptional practical

importance as it allows one to convert the array of numbers

-

the observed

structure amplitudes obtained from the experimentally measured intensities

-

Fundamentals

of

dzgraction

239

into the image of the atomic structure represented as the distribution of the

electron (or nuclear) density in the unit cell.

Thus, in the expanded form, the value of the electron density at any point

in the unit cell with coordinates x,

y

and

z

(0

5

x

5

1, 0

5

y

5

1 and

0

5

z

I

1) can be calculated using structure amplitudes obtained from x-ray

diffraction experiment as:

where

Fhkl

are the structure amplitudes represented as complex numbers.

Equation 2.132 may be converted into a more practical form since only

the absolute values of the structure amplitude

IF;;~

are directly observable

in a diffraction experiment. Thus,

1

h=+m

k=+m l=+m

=

-

z z

zlFi;lcos[2n(hx

+

ky

+

lz)

-

(2.133)

Pm

v

,,=* ,'=-a l=-m

where

ahkl

is the phase angle of the reflection

(hkl),

see Eq. 2.105.

When the crystal structure is centrosymmetric and contains no

anomalously scattering atoms, phase angles are fixed at

ahkl=

0 or

n

and Eq.

2.133 is simplified to

where

shkl=

1 or -1 for

a

hkl=

0 or

n,

respectively.

Taking into account Friedel's law the summation in Eqs. 2.132 to 2.134

can be simplified by excluding the negative values of one of the indices and

by changing the prefactor from 1/V to 2/V in order to keep the correct

absolute values of

pxyz.

Since no real experiment produces an infinite number

of data points (structure amplitudes), the practical use of Eqs. 2.132 through

2.134 is accomplished by including all available data, i.e. the summation is

truncated and carried over from

hmin

to

hmax, kmin

to

kmax

and

lmin

to

Imax.

Equation 2.133 is most commonly used to calculate the distributions of

the electron (nuclear) density in the unit cell, which are also known as

Fourier maps, from x-ray (neutron) diffraction data, respectively. The

locations of peaks on the Fourier map calculated using x-ray diffraction data

represent coordinates of atoms, while the electron density integrated over the

range of the peak corresponds to the number of electrons in the atom. The

major problem in using Eq. 2.133 is that only the absolute values of the

240 Chapter 2

structure amplitudes,

IF"^;,^,

are known directly from the experiment,

because they are obtained as square roots of the integrated intensities of the

corresponding Bragg peaks (Eq. 2.65) after eliminating all prefactors. As

already mentioned above, the information about phase angles

ahkl

(or signs,

shkl, see Eq. 2.134) is missing and is not measurable directly.

When the distribution of atoms in the unit cell is known at least

approximately,

e.g. when the model of the crystal structure exists, then the

phases can be easily computed from Eqs. 2.103 to 2.105,' and all parameters

in Eqs. 2.132 to 2.134 are defined. Examples of electron and nuclear density

distributions in the unit cell of the intermetallic compound

CeRhGe3

calculated from Eq. 2.133 by using x-ray and neutron powder diffraction

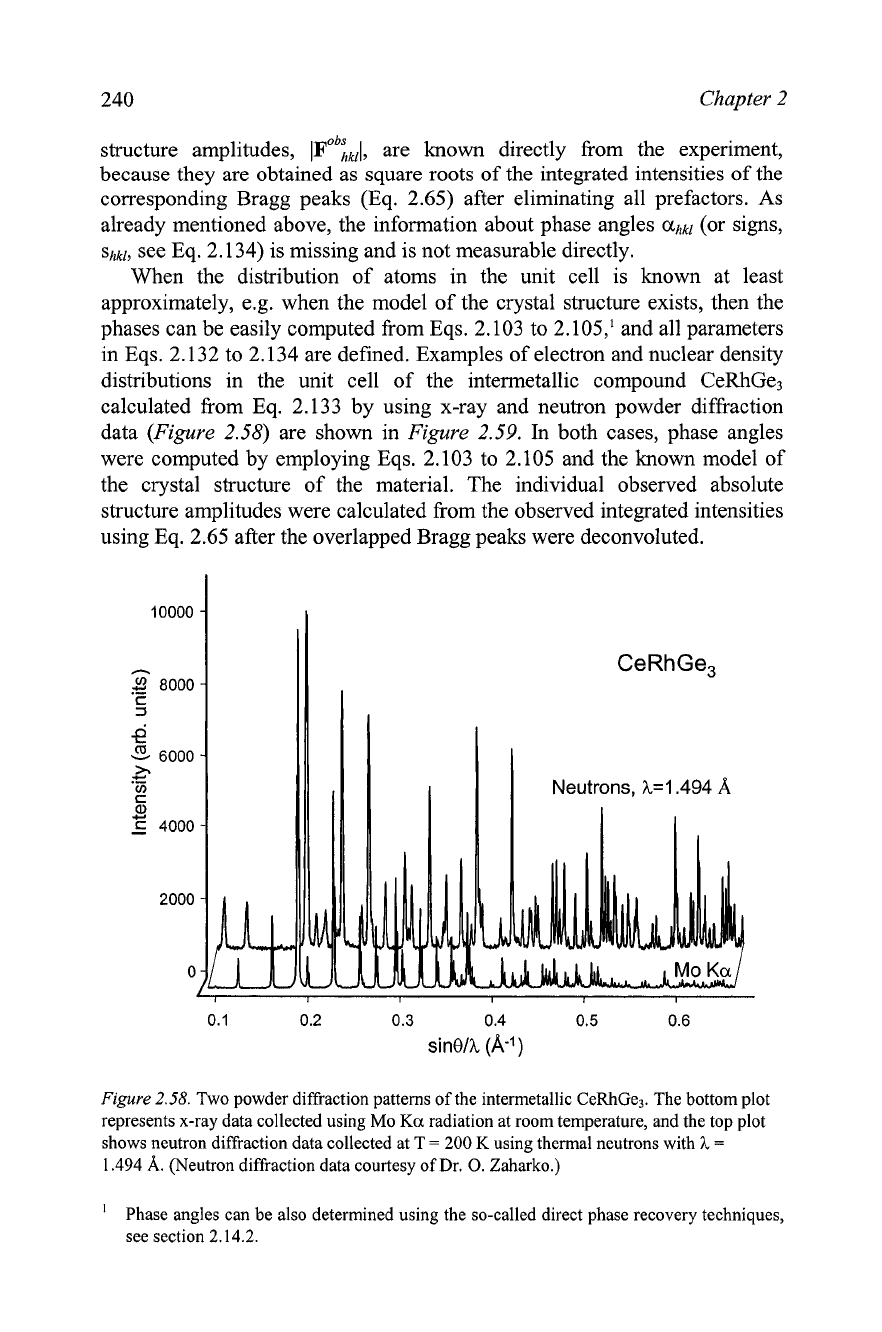
data (Figure 2.58) are shown in Figure 2.59.

In

both cases, phase angles

were computed by employing Eqs. 2.103 to 2.105 and the known model of

the crystal structure of the material. The individual observed absolute

structure amplitudes were calculated from the observed integrated intensities

using Eq. 2.65 after the overlapped Bragg peaks were deconvoluted.

Neutrons,

h=1.494

A

Figure

2.58.

Two powder diffraction patterns of the intermetallic CeRhGe3. The bottom plot

represents x-ray data collected using Mo

Ka

radiation at room temperature, and the top plot

shows neutron diffraction data collected at T

=

200

K

using thermal neutrons with

h

=

1.494

A.

(Neutron diffraction data courtesy of Dr.

0.

Zaharko.)

'

Phase angles can be also determined using the so-called direct phase recovery techniques,

see section 2.14.2.

Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.