Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffraction 24

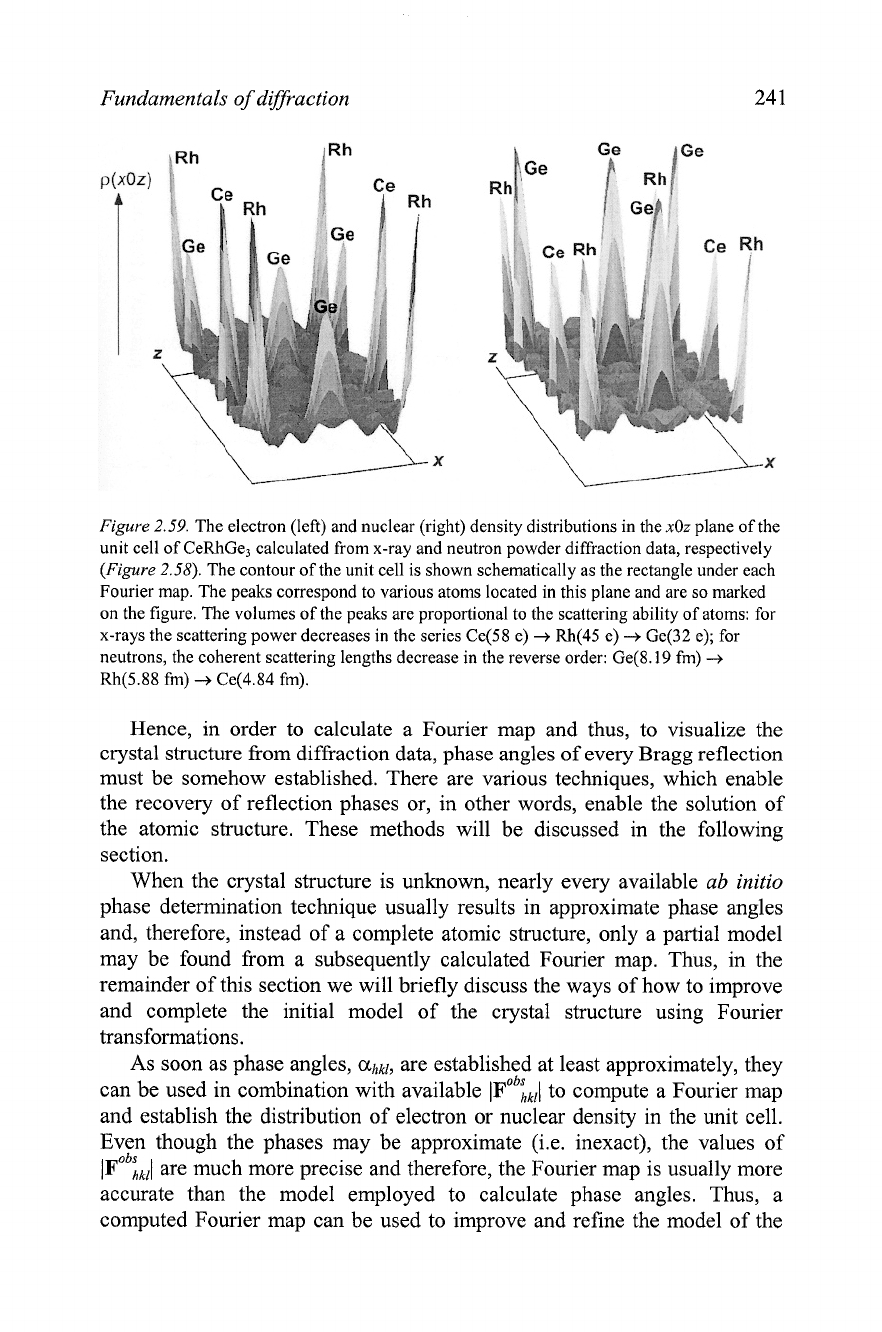
Figure 2.59. The electron (left) and nuclear (right) density distributions in the

xOz

plane of the

unit cell of CeRhGe3 calculated from x-ray and neutron powder diffraction data, respectively

(Figure 2.58). The contour of the unit cell is shown schematically as the rectangle under each

Fourier map. The peaks correspond to various atoms located in this plane and are so marked

on the figure. The volumes of the peaks are proportional to the scattering ability of atoms: for

x-rays the scattering power decreases in the series Ce(58 e)

Rh(45 e)

Ge(32 e); for

neutrons, the coherent scattering lengths decrease in the reverse order: Ge(8.19 fm)

Rh(5.88 fm)

Ce(4.84 fm).

Hence, in order to calculate a Fourier map and thus, to visualize the

crystal structure from diffraction data, phase angles of every Bragg reflection

must be somehow established. There are various techniques, which enable

the recovery of reflection phases or, in other words, enable the solution of

the atomic structure. These methods will be discussed in the following

section.

When the crystal structure is unknown, nearly every available

ab initio

phase determination technique usually results in approximate phase angles

and, therefore, instead of a complete atomic structure, only a partial model

may be found from a subsequently calculated Fourier map. Thus, in the

remainder of this section we will briefly discuss the ways of how to improve

and complete the initial model of the crystal structure using Fourier

transformations.

As soon as phase angles, ahkl, are established at least approximately, they

can be used in combination with available

IF"^",,^

to compute a Fourier map

and establish the distribution of electron or nuclear density in the unit cell.

Even though the phases may be approximate (i.e. inexact), the values of

IF"^:,^

are much more precise and therefore, the Fourier map is usually more

accurate than the model employed to calculate phase angles. Thus, a

computed Fourier map can be used to improve and refine the model of the

242

Chapter

crystal structure by finding coordinates of atoms with a higher precision

(when compared to the initial model) and by locating missing atoms.

If a crude initial model was used to determine approximate phases, some

atoms might not appear on the map, and these must be deleted because they

were not confirmed as a result of Fourier transformation. The new or

improved model is then used as a next level approximation to calculate the

new set of phase angles and a subsequent Fourier map must be calculated

using the new set of phases combined with experimental

/F"D",~~.

This process may be repeated as many times as needed until all atoms in

the unit cell are located and the following Fourier map(s) do not improve the

model. Equations 2.132 to 2.134 may be combined with a least squares

refinement using the observed data, which results in a more accurate model

of the crystal structure, including positional and displacement parameters of

the individual atoms already included in the model. The success in the

solution of the crystal structure is critically dependent on both the accuracy

of the initial model (initial set of phase angles) and the accuracy of the

experimental structure amplitudes. Needless to say, when the precision of

the latter is low, then the initial model should be more detailed and precise.

The effectiveness of Fourier transformation in locating missing atoms

may be improved by using the so-called difference Fourier map, which is

defined as

which is equivalent to Eq. 2.132, except that the observed complex structure

amplitudes are reduced by the complex structure amplitudes calculated from

the existing model. The resulting Fourier map, therefore, will not contain

"known" atoms and only the missing ones should become "visible". This

approach works especially well when locating weakly scattering atoms in the

presence of strong scatterers (e.g. when locating hydrogen atoms in organic

compounds) because the difference Fourier map reveals fine details, which

may be otherwise hidden in the background of the normal (Eq. 2.132) map.

The difference electron density distribution also finds an interesting

application when the fully refined model of the crystal structure is used to

compute a Fourier transformation. Although it may seem that such a Fourier

map should result in zero electron density throughout the unit cell (since the

differences in Eq. 2.135 are expected to approach zero), this is true only if

electron shells of atoms in the crystal structure were not deformed. In reality,

atoms do interact and form chemical bonds with their neighbors. This causes

a redistribution of the electron density when compared to isolated atoms, for

which atomic scattering functions are known.

Fundamentals of diffraction

243

Thus, the difference Fourier map calculated using Eq. 2.135 for a

complete and accurate model using highly precise x-ray diffraction data

reveals the so-called deformation electron density distribution. The latter is

essentially a difference between the electron density in a real crystal,

composed from chemically bound atoms, and individual isolated atoms or

ions, which sometimes enables the visualization of excess electron density

due to the formation of chemical bonds.' This technique has many

restrictions and requirements, the major of which are: extremely high

accuracy of the experimental diffraction data (including the accuracy of the

observed structure amplitudes) and availability of data at high

sinelh (often

low temperatures are required to achieve this). Unfortunately, powder

diffraction fails in the first requirement, except very simple structures, due to

the intrinsic and often unavoidable overlapping of Bragg reflections.

Other types of Fourier transformations may also be calculated when the

coefficients in Eq. 2.132 are modified or substituted. For example, when

obs

squared observed structure amplitudes IF

,,I

(in this case phase angles are

not required!) or normalized structure amplitudes E"~;, are used instead of

Fob",,, the resultant maps usually provide means to solve the crystal structure

(see next section). Different modifications of F"~;, may reveal the

distribution of the electrostatic potential and other properties of crystals.

2.14

Phase

problem

Despite the apparent simplicity with which a crystal structure can be

restored by applying Fourier transformation to diffraction data (Eqs. 2.132 to

2.135), the fact that the structure amplitude is a complex quantity creates the

so-called phase problem. In the simplest case (Eq. 2.133), both the absolute

values of the structure amplitudes and their phases (Eq. 2.105) are needed to

locate atoms in the unit cell. The former are relatively easily determined

from powder (Eq. 2.65) or single crystal diffraction data but the latter are

lost during the experiment.

Determination of the crystal structure of an unknown material is

generally far from a straightforward procedure, especially when only powder

diffraction data are available. It is truly a problem solving process and not a

simple refinement, which often may be fully automated. The latter is a

technique, which improves structural parameters of the approximately or

partially known model, usually by using a least squares minimization against

available diffraction data. It is worth noting that the least squares method is

See

V.G.

Tsirelson and

R.P.

Ozerov, Electron density and bonding in crystals: principles,

theory and x-ray diffraction experiments in solid state physics and chemistry, Institute of

Physics, Bristol,

(1996); P. Coppens, X-ray charge densities and chemical bonding.

IUCr Texts on Crystallography

Oxford University Press, Oxford, New York (1997)

Chapter

inapplicable to the

initio

structure solution because the structure

amplitude is a non-linear function of multiple individual atomic parameters

(Eq.

2.107).

Thus, during the crystal structure solving process phase angles,

which have been lost, must be recovered using suitable numerical technique.

large variety of methods, developed with a specific goal to solve the

crystal structure from diffraction data, can be divided into two major groups.

The first group entails techniques that are applicable in direct space by

constructing a model of the crystal structure from considerations other than

the available array of structure amplitudes. These include:

Purely geometrical modeling in the case of simple inorganic structures.

Examining various ways of packing and differences in conformations of

molecules with known geometry when dealing with molecular structures.

Finding analogies with closely related compounds, such as isostructural

series of intermetallics and partially isostructural host frameworks in

various intercalates.

Using a range of minimization methods, including quantum-chemical,

energy, entropy and geometry optimizations, and other recently

developed advanced techniques.

When one or more models are constructed, they are tested against the

experimental diffraction data. Often some of these approaches are combined

together but they always stem from the requirement that the generated model

must make physical, chemical and crystallographic sense. Thus, their

successful utilization requires a certain level of experience and knowledge of

how different classes of crystals are built, e.g. what to expect in terms of

coordination and bond lengths for a particular material based solely on its

chemical composition. Direct space modeling approaches will be discussed,

to some extent, in Chapter

The second group of methods uses an experimental array of diffraction

data, i.e. the absolute values of structure amplitudes, to provide initial clues

about the crystal structure of a material. Hence, they are applicable in the

reciprocal space. The first of the two reciprocal space methods, reviewed in

this section, is the Patterson technique, which is best known for its

applications in the so-called heavy atom method. Furthermore, as we will see

below, even though the phase angles of Bragg reflections are not directly

observed or measured, they are usually in certain relationships with one

another and with the absolute values of structure amplitudes. This property

supports a second reciprocal space approach, the so-called direct phase

determination techniques. The latter are always referred in a plural form

because they are based on several basic principles and usually contain

several different algorithms combined together. Needless to say, the crystal

structure determined using any of the reciprocal space methods should also

be reasonable from physical, chemical and crystallographic points of view.

Fundamentals of diffraction

245

2.14.1

Patterson technique

As suggested by Patterson' in 1934, the complex coefficients in the

forward Fourier transformation (Eqs. 2.129 and 2.132) may be substituted by

the squares of structure amplitudes, which are real, and therefore, no

information about phase angles is required to calculate the distribution of the

following density function in the unit cell:

Here, the multiplier 2 appears because only one-half of a reciprocal space is

used in the summation, thus the validity of Friedel's law is implicitly

assumed.

The resultant function, unfortunately, does not reveal the distribution of

atoms in the unit cell directly but it represents the distribution of interatomic

vectors, all of which begin in a common point

the origin of the unit cell.

Thus,

P,,,

is often called the function of interatomic vectors and it is also

known as the Patterson function of the ~~-~ourier series. The corresponding

vector density distribution in the unit cell is known as the Patterson map.

The interpretation of the Patterson function is based on a specific

property of Fourier transformation (denoted as

...I)

when it is applied to

convolutions

(8)

of functions:

As follows from Eq. 2.137, the multiplication of functions in the

reciprocal space (e.g. structure amplitudes) results in a convolution of

functions (e.g. electron or nuclear density) in the direct space, and

vice

versa.

Since Eq. 2.136 contains the structure amplitude multiplied by itself,

the resultant Patterson function, P,,, represents a self-convolution of the

electron (nuclear) density. Hence, it may be described as follows:

A.L.

Patterson,

Fourier series representation of the average distribution of the scattering

power in crystals, Phys. Rev. 45,763

(1934),

A.L.

Patterson,

Fourier series method for

the determination of the components of the interatomic distances in crystals, Phys. Rev.

46,372 (1934).

246 Chapter 2

where

P,,,

in every point (u, v, w) inside the unit cell is calculated as the

sum (integral) of products of the electron (nuclear) density at two points

separated by a vector (u, v, w).

For simplicity, assume that the distribution of electron or nuclear density

in the unit cell is discrete rather than continuous and is zero everywhere

except for the locations of atoms, viewed as dimensionless points (see

Figure 2.59, which illustrates that both electron and nuclear density

decreases rapidly away from the centers of atoms). Then, the result of

Eq.

2.138 is a set of peaks originating in (0, 0,

and ending at (u, v, w) with

heights (more precisely with peak volumes since atoms are not

dimensionless points),

Hy,

given as

where

and

are the number of electrons (or scattering lengths) of the ith

and

jth

atoms that are connected

a vector (u, v, w) defined as

+[xi

xj].

According to this interpretation of

Eq.

2.138, the value of the Patterson

function is zero at any other point in the unit cell.

example of an

idealized Patterson function corresponding to a simple two-dimensional

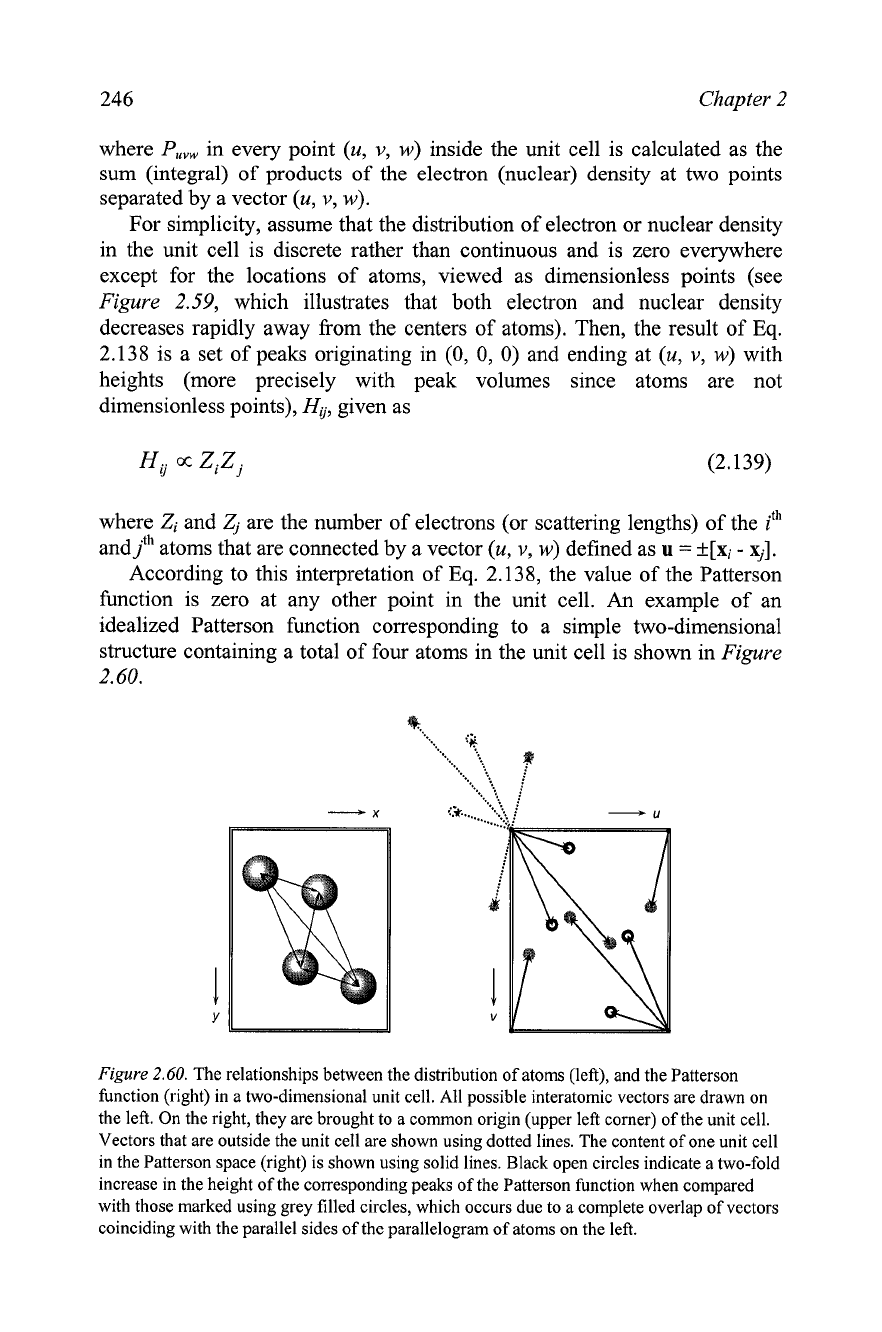
structure containing a total of four atoms in the unit cell is shown in Figure

Figure

2.60.

The relationships between the distribution of atoms (left), and the Patterson

function (right) in a two-dimensional unit cell. All possible interatomic vectors are drawn on

the left. On the right, they are brought to a common origin (upper left corner) of the unit cell.

Vectors that are outside the unit cell are shown using dotted lines. The content of one unit cell

in the Patterson space (right) is shown using solid lines. Black open circles indicate a two-fold

increase in the height of the corresponding peaks of the Patterson function when compared

with those marked using grey filled circles, which occurs due to a complete overlap of vectors

coinciding with the parallel sides of the parallelogram of atoms on the left.

Fundamentals

diffraction

247

Thus, since a Patterson map contains peaks, which are related to the real

distribution of atoms in the unit cell, it is possible to establish both the

coordinates of atoms and their scattering power by analyzing coordinates

and heights of Patterson peaks. Unfortunately, the analysis of the distribution

of interatomic vector density function is sometimes easier said than done due

to the presence of several complicating factors.

The first difficulty is that Patterson peaks are usually broader than

electron (nuclear) density peaks, which is the result of convolution (Eq.

2.138). The second complication is that the total number of Patterson peaks

in the unit cell equals to n(n-1), where n is the total number of atoms in the

unit cell (see Figure 2.60 where four atoms shown on the left produce

Patterson peaks shown on the right, four pairs of which are completely

overlapped). The third difficulty is derivative of the first two and it arises

from overlapping (often quite substantial) of different interatomic vectors.

example of the distribution of the interatomic vectors density function

in the uOw plane of CeRhGe3 is illustrated in Figure

2.61.

When compared

with the electron and nuclear density distributions (Figure 2.59), there are

many more peaks in the two Patterson maps. Similar to the results shown in

Figure 2.59, both Patterson functions are nearly identical except for the

distribution of peak intensities, which is expected due to the differences in

the scattering ability of Ce,

and Ge using x-rays and neutrons.

Figure

2.61. Patterson functions calculated in the uOw plane using

Eq. 2.136

and employing

experimental x-ray (left) and neutron (right) powder diffraction data shown in

Figure

2.58.

The strongest peak in any Patterson function is always observed at (0, 0, 0) because the

origins of all vectors coincide with the origin of coordinates. Since in this particular example

the real crystal structure contains an atom in (O,0,0, see

Figure

2.59), some of the peaks on

. .

the Patterson map correspond to the actual locations of atoms (i.e.

O).The contour of

the unit cell is shown schematically as the rectangle under each Patterson map.

248

Chapter

The complicating factors mentioned above, reduce the resolution of the

Patterson map, which may make it extremely difficult or impossible to

recover the atomic structure, especially in cases of complex crystal structures

containing many atoms with nearly equal atomic numbers, e.g. organic

compounds. On the other hand, when only a few atoms in the unit cell have

much stronger scattering ability than the rest, the identification of Patterson

peaks corresponding to these strong scatterers is relatively easy: according to

Eq. 2.139, these peaks will be stronger than all others, except for the peak at

the origin.

The application of the Patterson technique to locate strongly scattering

atoms is often called the heavy atom method (which comes from the fact that

heavy atoms scatter x-rays better and the Patterson technique is most often

applied to analyze x-ray diffraction data). This allows constructing of a

partial structure model ("heavy7' atoms only), which for the most part define

phase angles of all reflections (see Eq. 2.107). The "heavy atoms-only"

model can be relatively easily completed using sequential Fourier syntheses

(either or both standard, Eq. 2.133, and difference, Eq. 2.135), sometimes

enhanced by a least squares refinement of all found atoms.

The analysis of the Patterson hnction requires extensive use of

symmetry. Consider all possible interatomic vectors (calculated as uii

[xi

xj]) originating from an-atom in the general site position of the space

P2Jm, which are listed in

Table

2.18.

Only three of the vectors (shaded in

the first row of the table) are unique, and the relationships between them are

established by the combination of symmetry elements in the unit cell.

Table

2.18.

Interatomic vectors (shown in bold) produced by an atom located in the general

site position in the monoclinic crystal system, space group P2,Im.

Symmetry Symmetry

element

ooeration

XYJ

Thus, a vector 2x, 1/2,2z is the result of a 21 screw axis parallel to the

axis, and when the former is correctly identified on the Patterson map, the

two coordinates,

and z, of the corresponding atom are found.

second

vector

0, -112-2y, 0

is due to a mirror plane and it yields the missing

coordinate

while a vector 2x, 2y, 22 is due to a center of inversion, which

in this case could be used to confirm all three coordinates.

When a structure contains only a single independent heavy atom, the

solution is nearly always trivial. It may be possible to solve

structure with

two to four independent heavy atoms manually, even though the task

Fundamentals

diffraction 249

becomes much more challenging. Solving a structure from a Patterson map

in the case of more complex crystal structures is usually performed using

computer programs.

more detailed analysis of Table

2.18

indicates that symmetry of the

Patterson function is different from that of the original crystal structure. A

comprehensive examination of Patterson symmetry exceeds the scope of this

book. It can be shown, however, that symmetry elements with a translational

component, present in the space of the crystal structure, are transformed into

conforming finite symmetry elements in the Patterson function space except

for the lattice translations, which are preserved. Thus, screw axes become

rotation axes and glide planes are transformed into mirror planes. Moreover,

a center of inversion is always added to the symmetry of Patterson function.

For example, space group

P2,Im discussed above results in Patterson

symmetry corresponding to space group P2lm; 142m is transformed into

I4/mmm, Fdd2 turns into Fmmm, and so on. A complete list of Patterson

function symmetry for all space groups can be found in the International

Tables for Crystallography, vol.

2.14.2

Direct methods

this approach, the phase angles of reflections are derived directly from

the observed structure amplitudes through mathematical relationships

between intensities and indices of the reflections. The relationships are based

on the following postulations:

The electron density is non-negative anywhere in the unit cell, i.e.

p,,,

for all

2. The atomic structure is composed from nearly spherical atoms spread

nearly evenly throughout the unit cell volume.

These two general properties of the electron density result in special

relationships between phase angles of triplets of reflections, which have

arithmetically (but not symmetrically) related indices. The triplets of related

reflections are defined as follows

First reflection,

h, k, I

Second reflection,

h':

h', k', 1'

Third reflection,

h-h':

h-h',

k-k', 2-1'

The phase relationships within a triplet are not strict and their probability

depends on the magnitude of the associated structure amplitudes. The latter

are scaled and normalized in order to reduce their dependence on the atomic

scattering factor and vibrational motion since both reduce the structure

amplitude exponentially at high

sinelh, see

Eq.

2.91, Figure

2.53

and Figure

250 Chapter

2.55.

The normalized structure factor is commonly denoted as Ehkl and it is

calculated from the conventional structure factor as follows:

where the expected

estimated as:

(2.141)

average value of the structure factor,

<F',,>, is

and A(s) is the atomic scattering factor of the

jth

atom;

is sinelh of the

reflection (hkl).

the centrosymmetric structures, the relationships between the signs of

the reflections forming

triplet

(Eq.

2.140) are described by the Sayre

equation:'

where s

when

ahk,

(positive Fhkl),

-1 when

ahkl=

(negative

Fhkl), and the symbol

has a meaning of "probably equal", for example,

s123

s102s021.

The probability of this sign relationship in the triplet is defined as:

where

P+

is the probability of the positive sign for a reflection

and:

N-"'

lo:"

and

z,!"

Here

is the atomic number and

is the number of atoms in the unit cell.

the non-centrosymmetric structures, reflection phases in the triplet are

in the following relationship, also given by sayre:'

Sayre, The squaring method: a new method for phase determination, Acta Cryst.

(1952).