Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffraction

191

The two factors combined result in the following proportionality

Lcc

sin 8 sin 28

which after recalling that sin28

2sin8cos8 and ignoring all constants

(which are absorbed by the scale factor), becomes

The polarization factor arises from partial polarization of the

electromagnetic wave after scattering. Considering the orientation of the

electric vector, the partially polarized beam can be represented by two

components: one has its amplitude parallel (All) to the goniometer axis and

another has the amplitude perpendicular (AL) to the same axis. The

diffracted intensity is proportional to the square of the amplitude and the two

projections of the partially polarized beam on the diffracted wavevector are

proportional to

for (~11)~ and cos228 for (~1)~. Thus, partial polarization

after scattering yields the following overall factor (also see Thomson

equation in the footnote on page

140):

cos2 28

Pcc

When a monochromator is employed, it introduces additional

polarization, which is accounted as:

where 20M is the Bragg angle of the reflection from a monochromator (it is a

constant for a fixed wavelength), and

is the fractional polarization of the

beam. For neutrons

for unpolarized and unmonochromatized

characteristic x-ray radiation,

0.5

and ~0~28~

while for a

monochromatic or synchrotron radiation

should be established

experimentally (i.e. measured) or refined.

The Lorentz and polarization contributions to the scattered intensity are

nearly always combined together in a single Lorentz-polarization factor,

which in the case when no monochromator is employed is given as:

1+cos2 20

cos 0. sin2 0

Chapter

(2.70)

or assuming

0.5 with a crystal monochromator

Once again, all constant multipliers have been ignored in Eqs. 2.70 and

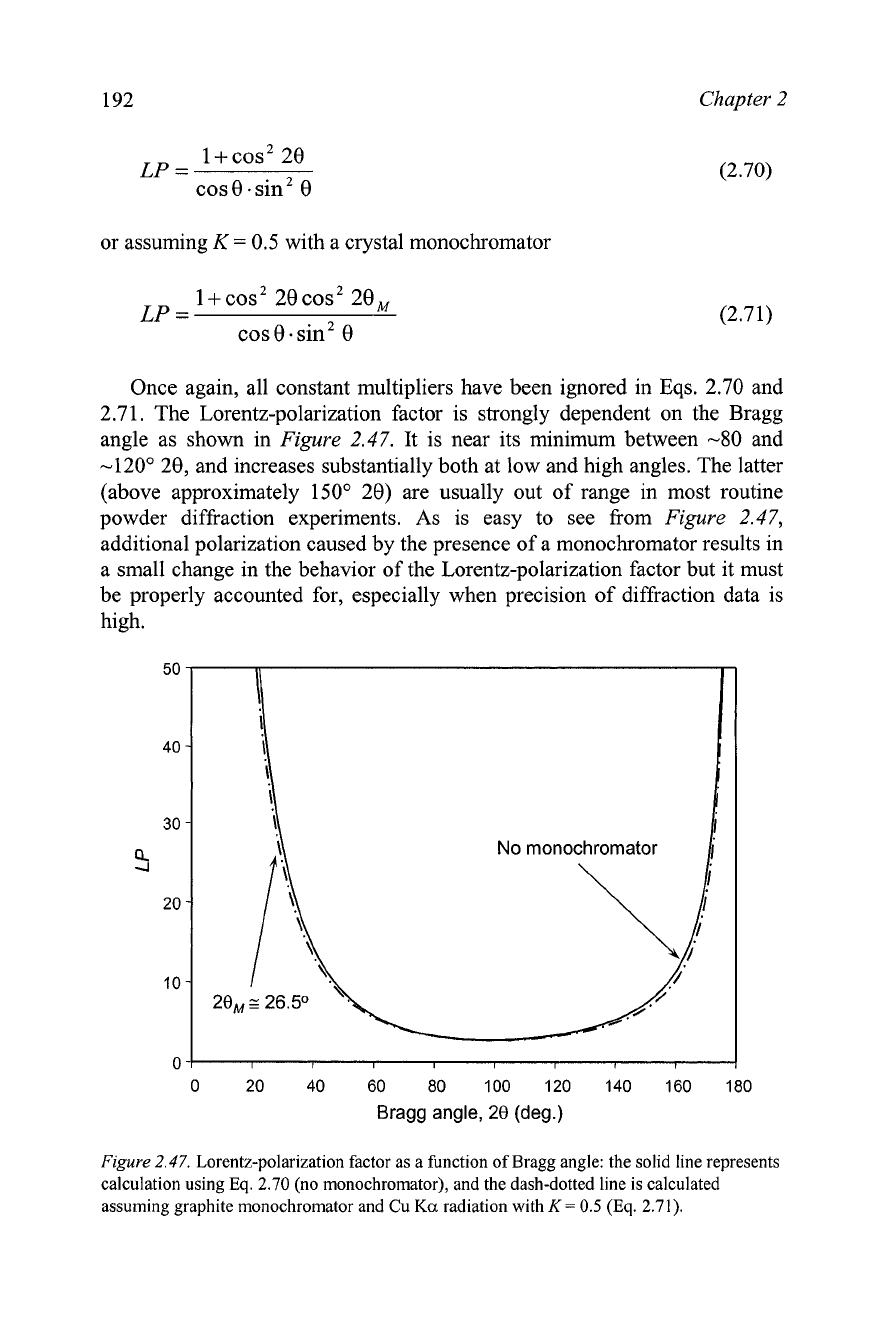
2.71. The Lorentz-polarization factor is strongly dependent on the Bragg

angle as shown in

Figure

2.47.

It is near its minimum between -80 and

-120" 20, and increases substantially both at low and high angles. The latter

(above approximately 150" 20) are usually out of range in most routine

powder diffraction experiments. As is easy to see from

Figure

2.47,

additional polarization caused by the presence of a monochromator results in

a small change in the behavior of the Lorentz-polarization factor but it must

be properly accounted for, especially when precision of diffraction data is

high.

No monochromator

28,

26.5O

I I

0 20 40 60 80 100 120 140 160 180

Bragg angle, 28 (deg.)

Figure

2.47.

Lorentz-polarization factor as a function of Bragg angle: the solid line represents

calculation using

Eq.

2.70 (no monochromator), and the dash-dotted line is calculated

assuming graphite monochromator and Cu

radiation with

0.5

(Eq.

2.71).

Fundamentals of diffraction

2.10.5 Absorption factor

Absorption effects in powder diffraction are dependent on both the

geometry and properties of the sample and the focussing method. For

example, when a flat sample is studied using the Bragg-Brentano technique,

the scattered intensity is not affected by absorption as long as the specimen

is highly impermeable and thick enough so that the incident beam never

penetrates all the way through the sample at any Bragg angle. On the

contrary, absorption by a thick flat sample in the transmission geometry has

considerable influence on the scattered intensity, much stronger than if a thin

sample of the same kind is under examination.

As established earlier (see Eqs. 2.7 and 2.8), intensity of the x-ray beam

or other type of radiation is reduced due to absorption after passing through

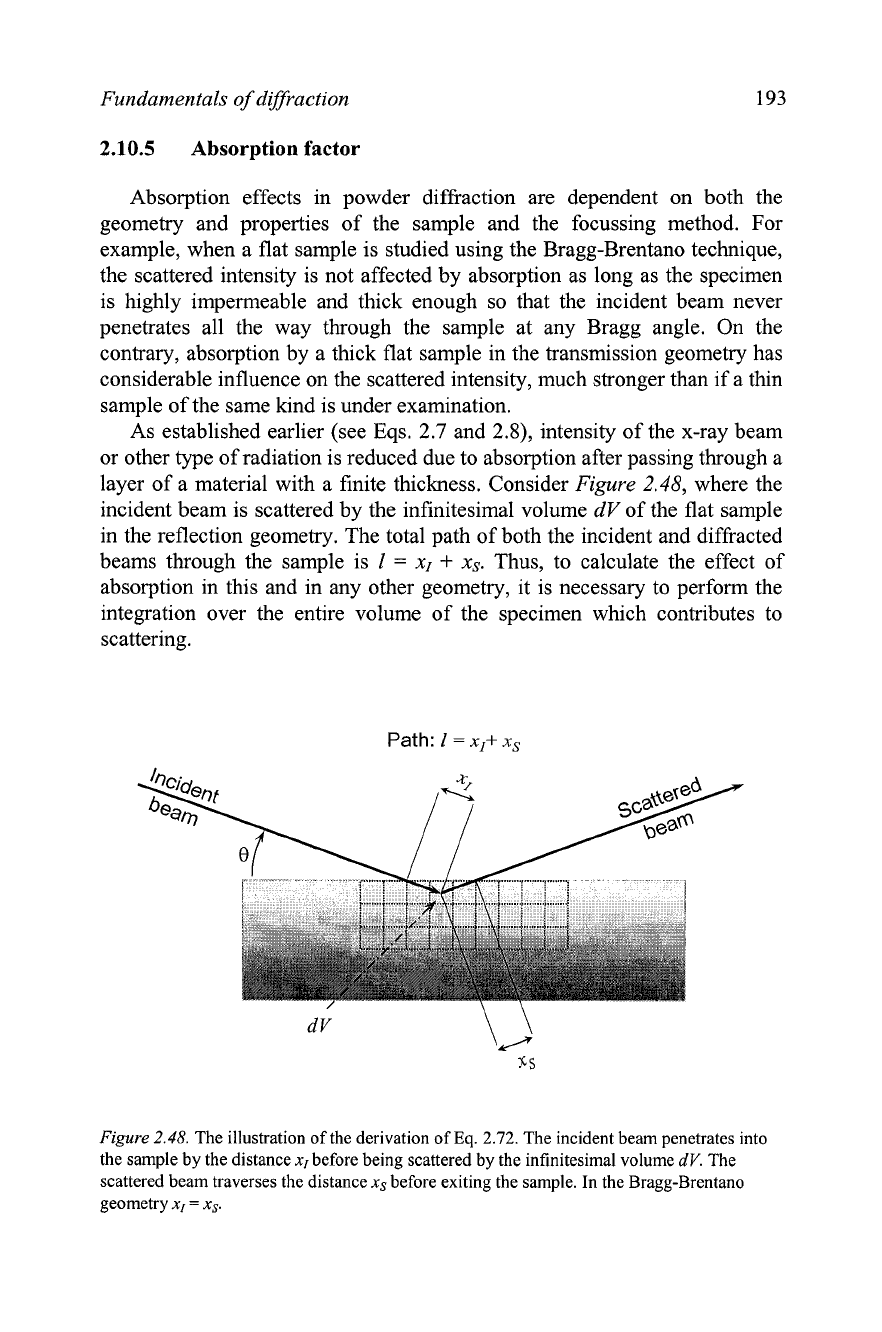
layer of a material with a finite thickness. Consider

Figure

2.48,

where the

incident beam is scattered by the infinitesimal volume

of the flat sample

in the reflection geometry. The total path of both the incident and diffracted

beams through the sample is

xs.

Thus, to calculate the effect of

absorption in this and in any other geometry, it is necessary to perform the

integration over the entire volume of the specimen which contributes to

scattering.

Path:

=x,+xs

Figure

2.48.

The illustration of the derivation of

Eq. 2.72.

The incident beam penetrates into

the sample by the distance

before being scattered by the infinitesimal volume

dV.

The

scattered beam traverses

the

distance

before exiting the sample. In the Bragg-Brentano

geometry

xs.

194

Chapter

Taking into account

Eq.

2.8, the following integral equation expresses the

reduction of the diffracted intensity,

as the result of absorption:'

It is important to recognize that an effective linear absorption coefficient,

pe~, has been introduced into Eq. 2.72 to account for a lower density of

dusted or packed powder when compared with the linear absorption

coefficient,

of the bulk. The latter is usually used in diffraction from

single crystals.

Eq. 2.72 can be solved analytically for all geometries usually employed

in powder diffracti~n.~ For the most commonly used Bragg-Brentano

focusing geometry the two limiting cases are as follows:

The material has very high linear absorption coefficient, or it is thick

enough so that there is a negligible transmission of the incident beam

through the sample at any Bragg angle. The resultant absorption factor in

this case is a constant and it is usually neglected in Eq. 2.65 because it

becomes a part of the scale factor:

The material has low linear absorption or the sample is thin so that the

incident beam is capable of penetrating all the way through the sample.

The absorption correction in this case is a function of Bragg angle as

shown in Eq. 2.74. Once again, the constant coefficient

1/2peff is usually

omitted since it becomes a part of the scale factor:

expi-2pe,t

sin

expi-2p,,

sin

(2.74)

2~eff

In single crystal diffraction, absorption correction is usually applied to the observed

intensities and therefore,

is sometimes called the transmission factor, while the

corresponding absorption correction is

1IA.

Analytical integration necessarily assumes that

ye,

remains constant, even though the

irradiated area of the specimen surface changes as a function of Bragg angle, as discussed

in Chapter

section

3.5.3.

When diffraction from a single crystal is of concern, analytical

solution of this equation is rarely possible and it is usually integrated numerically using the

known dimensions of a single crystal and the orientations of both the incident and

diffracted beams with respect to crystallographic axes for each individual reflection

hkl.

Fundamentals of diffraction 195

Eq. 2.74,

is sample thickness. Ignoring the absorption correction,

especially when

and/or

are small, which means a weakly absorbing or

thin sample, results in the underestimated calculated intensity at high Bragg

angles. As a result, unphysical (negative) values of thermal displacement

parameters are usually obtained.

The major

difficulty in applying an absorption correction (Eq. 2.74)

arises from usually unknown peff. Obviously, the linear absorption

coefficient,

p, can be easily calculated when the dimensions of the unit cell

and its content are known (see Eq. 2.10) but it is applicable only for a fully

dense sample. When a pulverized sample is used (and typically it is), p,ff

cannot be determined easily without measuring sample density. Often the

combined parameter (pefft) can be refined or estimated and accounted in

intensity calculations during Rietveld refinement (Chapter 7).

Another problem with pulverized samples is that their packing density

varies as a function of the depth. This is known as the porosity effect, and for

the Bragg-Brentano geometry, it may be expressed using two different

approaches:

The first has been suggested by Pitschke et

al.'

and the second by Suortti2

a,) exp(-a,

sin

a, exp(-a,

)

where a, and a2 are two variables that can be refined. Both approximations

account also for surface roughness as well as for absorption effects. They

give practically identical results and the only difference is that the Suortti

formula works better at low Bragg angles, according to Larsen and Von

D~eele.~

Approximations given in Eqs. 2.74 to 2.76 also account for some other

effects that distort intensity, for example improper size of the incident beam,

causing the beam to be broader than the sample at low Bragg angles. The

refinement of the corresponding parameters may become unstable because of

W. Pitschke,

Mattern, and H. Hermann, Incorporation of microabsorption corrections

into Rietveld analysis, Powder Diffraction

8,223

(1993).

P. Suortti, Effects of porosity and surface roughness on the x-ray intensity reflected from a

powder specimen,

Appl. Cryst.

325

(1972).

C.A.

Larsen and R.B. Von Dreele, General Structure Analysis System (GSAS), Los

Alamos National Laboratory Report, LAUR

86-748

(2000).

196

Chapter

correlations with some structural parameters (e.g. with the scale factor

and/or thermal displacement parameters of atoms). Therefore, any of these

corrections should be introduced

and/or refined with care.

2.10.6

Preferred orientation

Conventional theory of powder diffraction assumes completely random

distribution of the orientations among the infinite amount of crystallites in a

specimen used to produce a powder diffraction pattern.

other words,

precisely the same fraction of the specimen volume should be in the

reflecting position for each and every Bragg reflection. Strictly speaking this

is possible only when the specimen contains an infinite number of

crystallites.

practice it can be only achieved when the number of

crystallites is very large (usually in excess of lo6 to lo7 particles).

Nonetheless, even when the number of crystallites approaches infinity, this

does not necessarily mean that their orientations will be completely random.

The external shape of the crystallites plays an important role in achieving

randomness of their orientations in addition to their number.

When the shapes of crystallites are isotropic, random distribution of their

orientations is not a problem and deviations from an ideal sample are usually

negligible. However, quite often the shapes are anisotropic,

e.g. platelet-like

or needle-like and this results in the introduction of distinctly non-random

crystallite orientations due to natural preferences in packing of the

anisotropic particles. The non-random particle orientation is called preferred

orientation and it may cause considerable distortions of the scattered

intensity.

Preferred orientation effects are addressed by introducing the preferred

orientation factor in Eq. 2.65

andor by proper care in the preparation of the

powdered specimen. The former may be quite difficult and even impossible

when preferred orientation effects are severe. Therefore, every attempt

should be made to physically increase randomness of particle distributions in

the sample to be examined during a powder diffraction experiment. The

sample preparation will be discussed in Chapter

and in this section we will

discuss the modelling of the preferred orientation by various functions

approximating the radial distribution of the crystallite orientations.

Consider two limiting anisotropic particle shapes: platelet-like and

needle-like. The platelets, when packed in a flat sample holder, will tend to

align parallel to one another and to the sample surface.' Then, the amount of

plates that are parallel or nearly parallel to the surface will be much greater

than the amount of platelets that are perpendicular or nearly perpendicular to

the surface.

this case, a specific direction that is perpendicular to the flat

Also see the schematic shown in

Figure

3.20

in Chapter

Fundamentals

diffraction

197

sides of the crystallites is called the preferred orientation axis. It coincides

with a reciprocal lattice vector d*Thkl that is normal to the flat side of each

crystallite. Therefore, intensity of reflections from reciprocal lattice points

with vectors parallel to

d*Thkl will be larger than intensity of reflections

produced by any other point of the reciprocal lattice (minimum for those

with reciprocal lattice vectors perpendicular to d*Thkl) simply because the

distribution of their orientations is highly anisotropic. The preferred

orientation in cases like that is said to be uniaxial, and the preferred

orientation axis is perpendicular to the surface of the flat specimen.

The needle-like crystallites, when packed into a flat sample, will also

tend to align parallel to the surface.' However, the preferred orientation axis,

which in this case coincides with the elongated axes of the needles, will be

parallel to the sample surface.

addition to the nearly unrestricted

distribution of needles' axes in the plane parallel to the sample surface

(which becomes nearly ideally random when the sample spins around an axis

perpendicular to its surface), each needle may be freely rotated around its

longest direction. Hence, if the axis of the needle coincides, for example,

with the vector

d*Thkl, then reflections fiom reciprocal lattice points with

vectors parallel to

d*Thkl will be suppressed to a greater extent and reflections

from reciprocal lattice points with vectors perpendicular to d*Thkl will be

strongly increased. This example describes the so-called in-plane preferred

orientation.

both cases the most affected is the intensity of Bragg peaks that

correspond to reciprocal lattice points that have their corresponding

reciprocal lattice vectors parallel or perpendicular to d*Thkl, while the effect

on intensity of other Bragg peaks is intermediate. Hence the preferred

orientation effect on the intensity of any reflection

hkl

can be described as a

radial function of angle

ohkl

between the corresponding vector dfhkl and a

specific d*Thk~, which is the preferred orientation direction. The angle $hkl can

be calculated from:

where dXhkl is the reciprocal lattice vector corresponding to a Bragg peak

hkl

and d*Thkl is the reciprocal lattice vector parallel to the preferred orientation

axis. The numerator is a scalar product of the two vectors and the

denominator is a product of the lengths of two vectors.

The simplest radial function that describes the anisotropic distribution of

the preferred orientation factor as a function of angle

$hkl

is an ellipse

Also see the schematic shown in

Figure

3.20

in Chapter

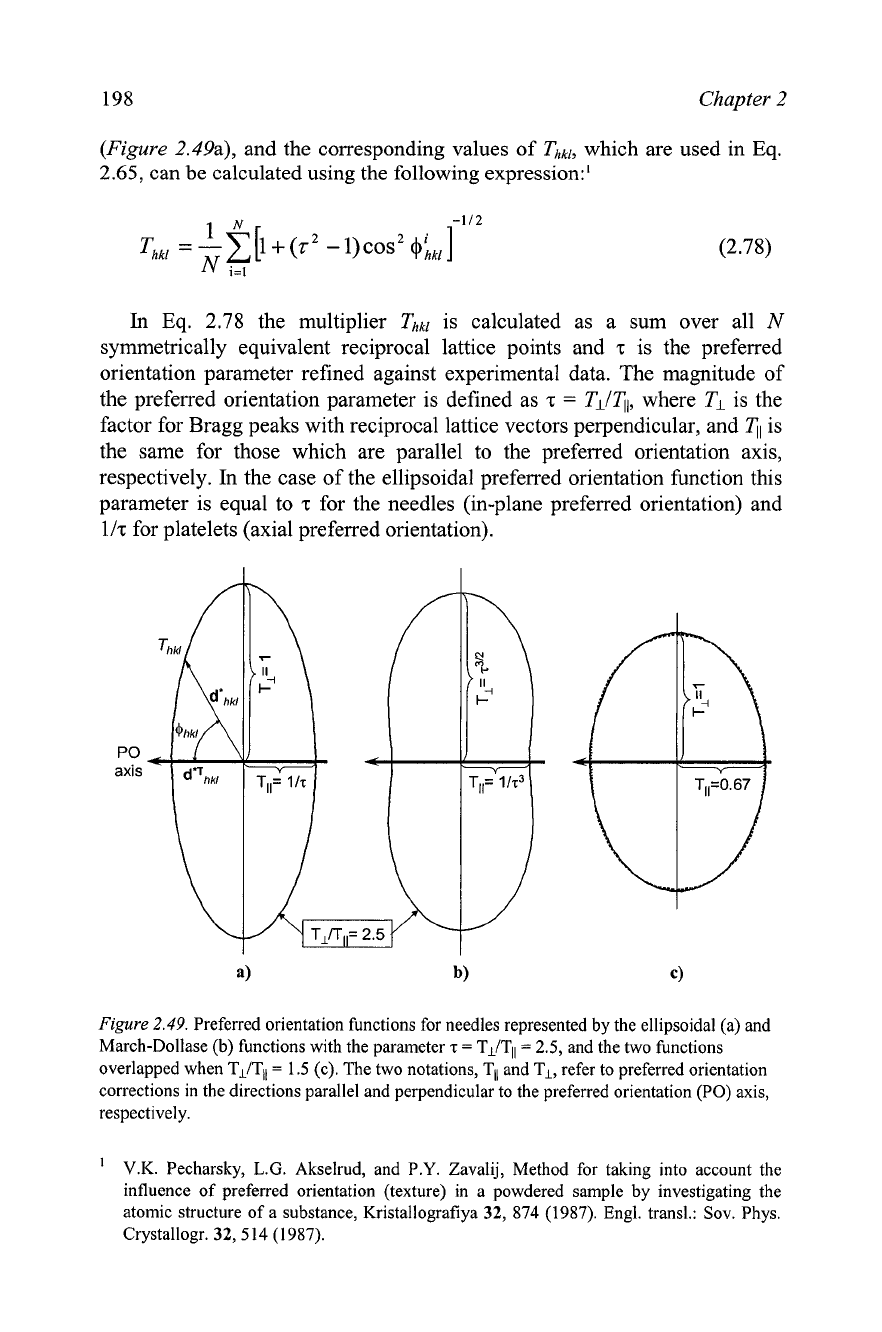
198 Chapter 2

(Figure 2.49a), and the corresponding values of

Thkl,

which are used in Eq.

2.65,

can be calculated using the following expression:'

Eq.

2.78

the multiplier

Thkl

is calculated as a sum over all

symmetrically equivalent reciprocal lattice points and

is the preferred

orientation parameter refined against experimental data. The magnitude of

the preferred orientation parameter is defined as

TL/qI, where Tl is the

factor for Bragg peaks with reciprocal lattice vectors perpendicular, and

the same for those which are parallel to the preferred orientation axis,

respectively.

the case of the ellipsoidal preferred orientation function this

parameter is equal to

for the needles (in-plane preferred orientation) and

l/z for platelets (axial preferred orientation).

axis

Figure

2.49.

Preferred orientation functions for needles represented by the ellipsoidal (a) and

March-Dollase (b) functions with the parameter

Tl/TII

2.5,

and the two functions

overlapped when

Tl/TII

1.5

(c). The two notations,

TII

and

Tl,

refer to preferred orientation

corrections in the directions parallel and perpendicular to the preferred orientation (PO) axis,

respectively.

V.K. Pecharsky,

L.G.

Akselrud, and P.Y. Zavalij, Method for taking into account the

influence of preferred orientation (texture) in a powdered sample by investigating the

atomic structure of a substance, Kristallografiya

32,

874 (1987). Engl. transl.: Sov. Phys.

Crystallogr.

32,

(1987).

Fundamentals of diffraction

199

different approach has been suggested by Dollase,' where the preferred

orientation factor is represented by a more complex March-Dollase function:

Here the preferred orientation parameter,

T~",

represents needles and its

inverse represents plates.

example of the March-Dollase preferred

orientation function for needles with magnitude TL/qI

2.5 is shown in

Figure

2.49b.

both cases (Eqs. 2.78 and 2.79) the preferred orientation factor Thkl is

proportional to the probability of the point of the reciprocal lattice,

hkl,

to be

in the reflecting position (i.e. the probability of being located on the surface

of the Ewald's sphere).

other words, this multiplier is proportional to the

amount of crystallites with

hkl

planes parallel to the surface of the flat

sample.

Both approaches work in a similar way.

the case of platelet-like

particles, the function is stretched along TI! (TII

TL), while in case of

needles it is stretched along TL (TI/

TI). Therefore, in both cases

describes preferred orientation of the platelets and

1 describes preferred

orientation of the needles. Obviously

1 corresponds to a completely

random distribution of reciprocal lattice vectors and the corresponding radial

distribution functions become a circle with unit radius (both

Eq.

2.78 and

2.79 result in Thki

for any +hki).

Both functions give practically the same result at low and moderate

degrees of non-randomness (i.e. at low preferred orientation contribution).

The example with TL/qi

1.5 is shown in

Figure

2.49c, where the two

functions (Eqs. 2.78 and 2.79) are nearly indistinguishable. Unfortunately,

strong preferred orientation cannot be adequately approximated by either of

these functions and the best way around it is to reduce the preferred

orientation by properly preparing the sample.

The platelets and needles discussed above are the two limiting but still

the simplest possible cases. Particles may (and often do) have shapes of

ribbons. These particles will pack the same way needles do

parallel to the

sample surface but the ribbons will not be randomly oriented around their

longest axes

they will tend to align their flat sides parallel to the sample

surface. This case should be treated using two different preferred orientation

functions simultaneously: one along the needle and one perpendicular to its

W.A. Dollase, Correction of intensities for preferred orientation in powder diffractometry:

Application of the March model,

Appl. Cryst.

19,267

(1986).

200 Chapter

flat surface. Thus, both types of functions (Eqs. 2.78 and 2.79) can be

modified as follows:

where

Ttotai

is the overall preferred orientation correction,

Nfl

is the number of

different preferred orientation axes,

is the preferred orientation correction

for the

ith

axis, and ki is the corresponding scale factor, which reflects the

contribution of each axis. Here,

is the portion of the sample not affected

by preferred orientation at all. Eq. 2.80 is sometimes used even when only

one kind of the preferred orientation is present, thus giving the following

very simple expression

Yet another approach, which is based on the algorithm described by

Bunge,' uses spherical harmonics expansion to deal with preferred

orientation in three dimensions as a complex radial distribution:

where

h represents reflection, and

sample orientations;

is the maximum order of a harmonic;

C;"" are harmonic coefficients;

k(h) and k@) are harmonic factors as functions of reflection and sample

orientations, respectively.

The expression for harmonic factors is complex and is defined

azimuthally by means of a Lagrange function. Sample orientation in routine

powder diffraction experiment is fixed and so is the corresponding harmonic

factor k(y), which simplifies

Eq.

2.82 to:

H.-J.

Bunge, Texture analysis in materials science, Buttenvorth, London

(1982).