Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffraction 171

An example of how important the sample displacement correction may

become is shown in Figure

2.41,

where the differences between the observed

and calculated Bragg angles are in the -0.03 to +0.04' range before

correction (open circles). They fall within the -0.01 to +O.O1•‹ range (filled

triangles) when the sample displacement parameter was refined together

with the unit cell dimensions. Even though the difference in the unit cell

dimensions obtained with and without the sample displacement correction

(Figure 2.41) is not exceptionally large, it is still ten to twenty times the least

squares standard deviations,

i.e. the differences in lattice parameters are

statistically significant.

2.9

Shapes of powder diffraction peaks

All but the simplest powder diffraction patterns are composed from more

or less overlapped Bragg peaks due to the intrinsic one-dimensionality of the

powder diffraction technique coupled with the usually large number of

"visible" reciprocal lattice points,

i.e. those that have d*hkl

211, and the

limited resolution of the instrument (e.g. see the model in Figure 2.38d and

Figure 2.32). Thus, processing of the data by fitting peak shapes to a suitable

function is required in order to obtain both the positions and intensities of

individual Bragg peaks. The same is also needed in structure refinement

using the full profile fitting approach

the Rietveld method.

The observed peak shapes are best described by the so-called peak shape

function (PSF), which is a convolution' of three different functions:

instrumental broadening, Q, wavelength dispersion,

and specimen

function,

Thus, PSF can be represented as follows:

where

is the background function.

The instrumental function, Q, depends on multiple geometrical

parameters: the locations and geometry of the source, monochromator(s),

convolution

(8)

of two functions,

and

is defined as an integral

which expresses the amount of overlap of one function g as it is shifted over another

function$ It, therefore, "blends" one function with another. The convolution is also known

as "folding" (e.g. see E.W. Weisstein, Convolution, Eric Weisstein's world of

mathematics,

http://mathworld.wolfram.corn/Convolution.html).

172

Chapter

slits, and specimen. The wavelength (spectral) dispersion function,

accounts for the distribution of the wavelengths in the source and it varies

depending on the nature of the source, and the monochromatization

technique. Finally, the specimen function,

originates from several effects.

First is dynamic scattering, or deviations from the kinematical model. They

yield a small but finite width (the so-called Darwin width) of the Bragg

peaks. The second effect is determined by the physical properties of the

specimen: crystallite (grain) size and microstrains. For example, when the

crystallites are small (usually smaller than

-1pm) and/or they are strained,

the resultant Bragg peak widths may increase substantially.

It is worth noting that unlike the instrumental and wavelength dispersion

functions, the broadening effects introduced by the physical state of the

specimen may be of interest in materials characterization. Thus, effects of

the average crystallite size

(z)

and microstrain

(E)

on Bragg peak broadening

(p, in radians) can be described in the first approximation as follows:

and

where

is a constant that depends on the definition of a microstrain. It is

important to note that

in Eqs. 2.46 and 2.47 is not the total breadth of a

Bragg peak but it is an excess width, which is.an addition to all instrumental

contributions. The latter is usually established by measuring a standard

material without microstrain and grain size effects at the same experimental

conditions.

general, three different approaches to the description of peak shapes

can be used. The first employs

empirical

peak shape functions, which fit the

profile without attempting to associate their parameters with physical

quantities. The second is a

semi-empirical

approach that describes

instrumental and wavelength dispersion functions using empirical functions,

while specimen properties are modeled using realistic physical parameters.

the third, the so-called

fundamental parameters

approach,' all three

components of the peak shape function (Eq. 2.45) are modeled using rational

physical quantities.

Bergmann, Contributions to evaluation and experimental design in the fields of x-ray

powder diffractometry, Ph.D. thesis (in German), Dresden University for Technology

(1984).

See

http://www.bgmn.de/methods.html

for more information and other references.

Fundamentals of diffraction 173

2.9.1

Peak

shape

functions

Considering Figure 2.38, Figure 2.39 and

Eq.

2.45, the intensity, Y(i), of

the i" point (1

n, where n is the total number of measured points) of

the powder diffraction pattern, in the most general form is the sum of the

contributions,

yk,

from the m overlapped individual Bragg peaks (1

and the background, b(i). Therefore, it can be described using the following

expression:

Y(i)

b(i)

(x,)

0.5~~

(x,

Ax,)]

k=l

where:

is the intensity of the

Bragg reflection,

20i

29, and

Axk

the difference between the Bragg angles of the

Ka2

and

Kal

components in

the doublet (if present). The presence of Bragg intensity as a multiplier in

Eq.

2.48 enables one to introduce and analyze the behavior of different

normalized functions independently of peak intensity, i.e. assuming that the

definite integral of a peak shape function, calculated from negative to

positive infinity, is unity in each case.

The four most commonly used empirical peak shape functions

are as

follows:

Gauss:

Lorentz:

Pseudo-Voigt

c2/

(2.5 1)

T,)-(I+

cLx2)-'

.nH

174

Chapter

where:

Hand

IT,

are the full widths at half maximum (often abbreviated as

FWHM).

(20,

~O,)/H,

is essentially the Bragg angle of the

ith

point in the

powder diffraction pattern with its origin in the position of the

kth

peak

divided by the peak's FWHM.

20i, is the Bragg angle of the

ith

point of the powder diffraction pattern;

20k, is the calculated (or ideal) Bragg angle of the

kth

Bragg reflection.

1n 2

and

ci2

/&H

is the normalization factor for the Gauss

function such that [~(x)dx

4, and

c:"

/ZH'

is the normalization factor for the Lorentz

function such that [~(x)dx

4(2'ID

and [T(P)/T(P

112)]~:~

/AH

is the

normalization factor for the Pearson-VII function such that

tan2 0

tan0

wYI2, which is known as Caglioti formula, is

the full width at half maximum as a function of 8 for Gauss, pseudo-

Voigt and Pearson-VII functions, and U,

and Ware free variables.'

cos

tan

is the full width at half maximum as a function

of 0 for the Lorentz function, and U and

are free variables.

202, where

is the pseudo-Voigt function

mixing parameter, i.e. the fractional contribution of the Gauss function

into the linear combination of Gauss and Lorentz functions, and

qo,

and q2 are free variables.

Caglioti,

Paoletti, and F.P. Ricci, Choice of collimators for a crystal spectrometer for

neutron diffraction, Nucl. Instrum. Methods 3,223

(1958).

Fundamentals

diffraction

175

r, is the gamma function.'

120

~~/(20)~

is the exponent as a function of Bragg

angle in the Pearson-VII function, and Po,

and

are free variables.

The two simplest peak shape functions (Eqs.

2.49

and

2.50)

represent

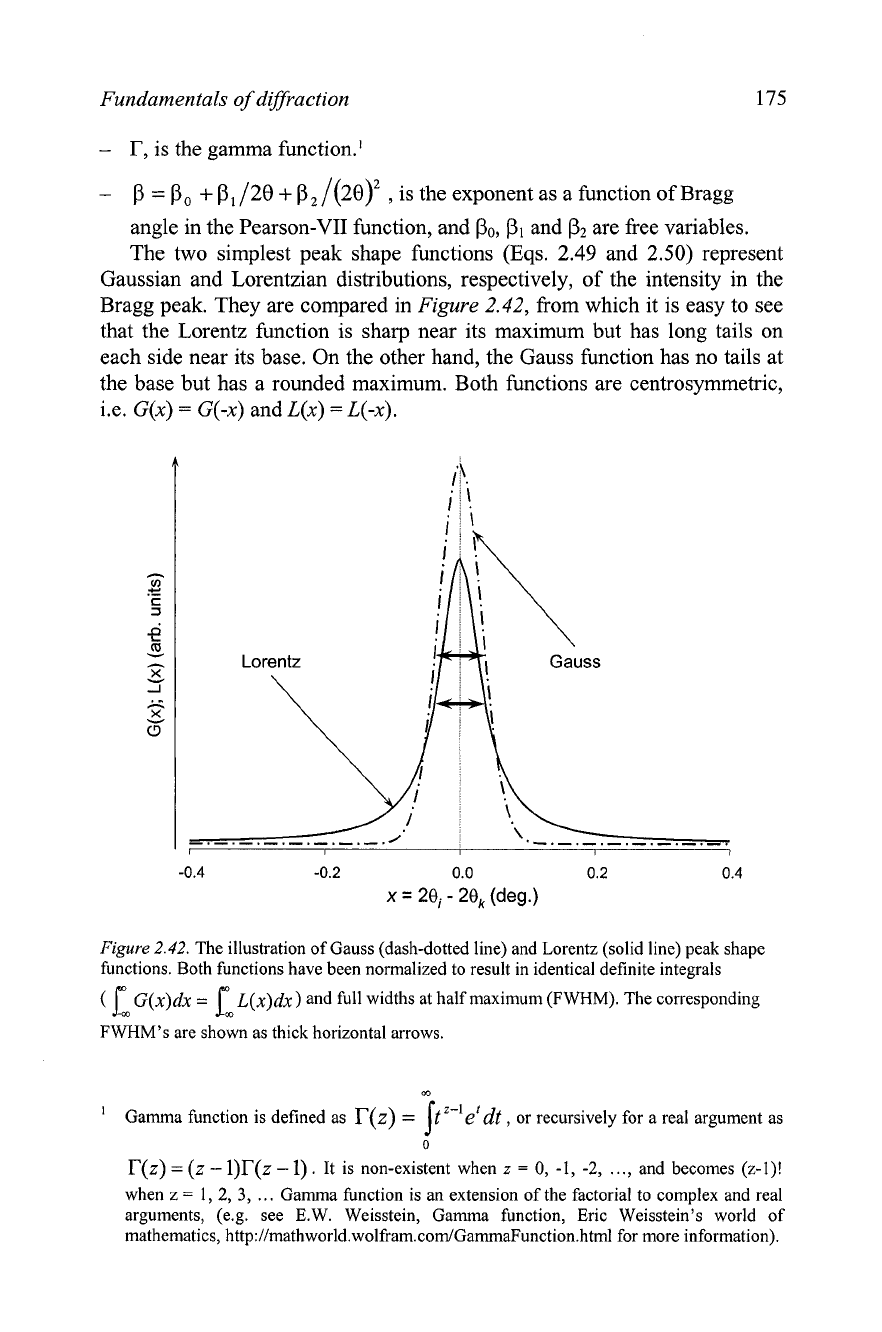
Gaussian and Lorentzian distributions, respectively, of the intensity in the

Bragg peak. They are compared in

Figure

2.42, from which it is easy to see

that the Lorentz function is sharp near its maximum but has long tails on

each side near its base. On the other hand, the Gauss function has no tails at

the base but has a rounded maximum. Both functions are centrosymmetric,

i .e.

G(x)

G(-x) and L(x)

L(-x)

-0.4 -0.2 0.0 0.2 0.4

28,

20,

(deg.)

Figure

2.42.

The illustration of Gauss (dash-dotted line) and Lorentz (solid line) peak shape

functions. Both functions have been normalized to result in identical definite integrals

(

G(x)dx

L(x)dx) and full widths at half maximum (FWHM). The corresponding

m m

FWHM's are shown as thick horizontal arrows.

Gamma function is defined as

r(z)

Stz-'e'dt

or recursively for a real argument as

T(z)

l)T(z

It is non-existent when z

-1,

-2,

..,

and becomes (z-I)!

when z

. .

Gamma function is an extension of the factorial to complex and real

arguments, (e.g. see E.W. Weisstein, Gamma function, Eric Weisstein's world of

mathematics,

http://mathworld.wolfram.com/GammaFunction.html

for more information).

176

Chapter

The shapes of real Bragg peaks, which are the results of convoluting

multiple instrumental and specimen functions

(Eq.

2.45),

are rarely

described well by simple Gaussian or Lorentzian distributions, especially in

x-ray diffraction. Usually real peak shapes are located somewhere between

the Gauss and Lorentz distributions and they can be better represented as the

mixture of the two functions.'

ideal way would be to convolute the Gauss

and Lorentz functions in different proportions. This convolution, however, is

a complex procedure, which requires numerical integration every time one or

several peak shape function parameters change. Therefore, a much simpler

linear combination of Gauss and Lorentz functions is used instead of a

convolution, and it is usually known as the pseudo-Voigt function (Eq. 2.5 1).

The Gaussian and Lorentzian are mixed in

q to 1-q ratio, so that the value of

the mixing parameter,

q, varies from 0 (pure Lorentz) to 1 (pure Gauss).

Obviously, q has no physical sense outside this range.

The fourth commonly used peak shape function is Peasron-VII (Eq.

2.52). It is similar to Lorentz distribution except that the exponent

(P) varies

in the Pearson-VII, while it remains constant

1) in the Lorentz function.

Pearson-VII provides an intensity distribution close to the pseudo-Voigt

function: when the exponent,

1, it is identical to the Lorentz distribution,

and when

10, Pearson-VII becomes nearly pure Gaussian. Thus, when

the exponent is in the range 0.5

1 or

10, the peak shape extends

beyond Lorentz or Gauss functions, respectively, but these values of

are

rarely observed in practice. An example of the x-ray powder diffraction

profile fitting using Pearson-VII function is shown in

Figure

2.43.

Both the

pseudo-Voigt and Pearson-VII functions are also centrosymmetric.

The argument, x, in each of the four empirical functions establishes the

location of peak maximum, which is obviously observed when x

0 and

20i

2ek.

second parameter, determining the value of the argument, is the

full width at half maximum,

The latter varies with 28 and its dependence

on the Bragg angle is most commonly represented by an empirical peak

broadening function, which has three free parameters

and

(except

for the pure Lorentzian, which usually has only two free parameters). Peak

broadening parameters are refined during the profile fitting. Hence, in the

most general case the peak full width at half maximum at a specific 28 angle

is represented as

The most notable exception is the shape of peaks in neutron powder diffraction (apart from

the time-of-flight data), which is typically close to the pure Gaussian distribution. Peak

shapes in

TOF

experiments are usually described by a convolution of exponential and

pseudo-Voigt functions.

Fundamentals

diffraction

177

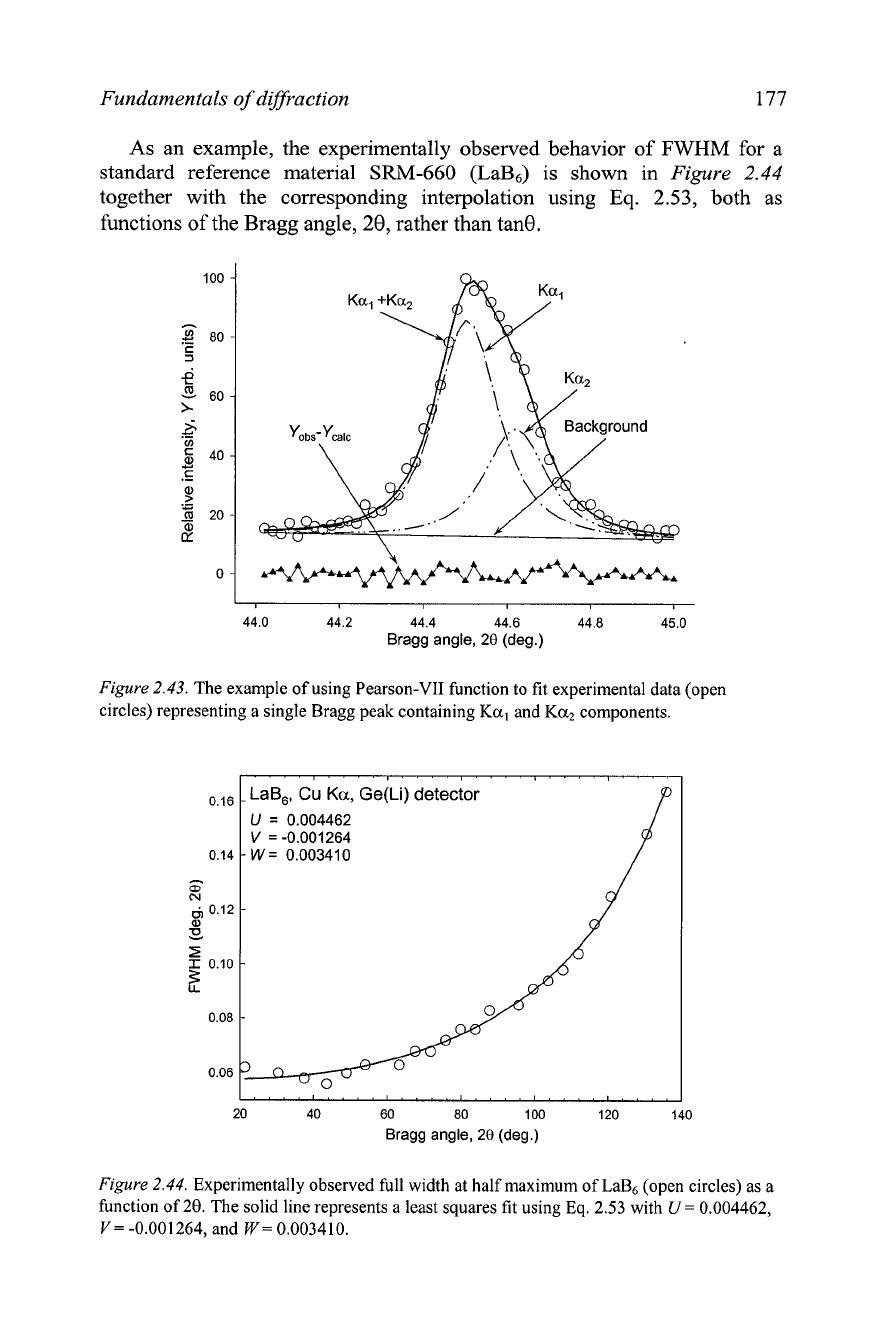
As an example, the experimentally observed behavior of

FWHM

for a

standard reference material

SRM-660

(LaB6) is shown in

Figure

2.44

together with the corresponding interpolation using

Eq.

2.53, both as

functions of the Bragg angle, 20, rather than tan0.

44.0 44.2 44.4 44.6 44.8 45.0

Bragg angle,

(deg.)

Figure

2.43.

The example of using Pearson-VII function to fit experimental data (open

circles) representing a single Bragg peak containing

Ka,

and

Kaz

components.

100

120 140

Bragg angle,

(deg.)

Figure

2.44.

Experimentally observed full width at half maximum of La& (open circles) as a

function of 20. The solid line represents a least squares fit using Eq. 2.53 with

0.004462,

-0.001264, and

0.003410.

178

Chapter

It is worth noting that the Lorentzian broadening function

(IT)

parameters,

and

have the same dependence on Bragg angle as crystallite

size- and microstrain-related broadening (compare Eqs. 2.46 and 2.47 with

Eq. 2.50 and following explanation of notations). Therefore, when Bragg

peaks are well represented by the pure Lorentz distribution, these physical

characteristics of the specimen can be calculated from FWHM parameters

after the instrumental and wavelength dispersion parts are subtracted.

The mixing coefficient,

for pseudo-Voigt function and the exponent,

for Pearson-VII function, generally vary for a particular powder diffraction

pattern. Their behavior is typically modeled with a different empirical

parabolic function of tan9 and 29, respectively, as follows from equations

2.51 and 2.52. Peak shapes in the majority of routinely collected x-ray

diffraction patterns are reasonably well represented using pseudo-Voigt

and/or Pearson-VII functions. On the other hand, noticeable improvements

in the experimental powder diffraction techniques, which occurred in the last

decade, resulted in the availability of exceptionally precise and high

resolution data, especially when employing synchrotron radiation sources,

where the use of these relatively simple functions is no longer justified.

Furthermore, the ever-increasing computational power facilitates the

development and utilization of advanced peak shape functions, including

those that extensively use numerical integration.

Most often, various modifications of the pseudo-Voigt function are

employed to achieve improved precision, enhance the asymmetry

approximation, account for the anisotropy of Bragg peak broadening, etc.

For example, a total of four different functions (not counting those for the

time-of-flight experiments) are employed in

GSAS.'

The first function is the

pure Gaussian (Eq. 2.49), which is suitable for neutron powder diffraction

patterns. The second is a modified pseudo-Voigt (the so-called Thompson

modified

pseudo-V~igt),~ where the function itself remains identical to

Eq.

2.51 but it employs

multi-term Simpson's integration introduced by

C.J.

H~ward.~ Its FWHM

(H)

and mixing

(q)

parameters are modeled as follows:

C.A. Larsen and R.B. Von Dreele, GSAS: General structure analysis system. LANL, Los

Alamos, New Mexico, USA (2000). The cited user manual and software are freely

available

via

FTP

ftp://ftp.lanl.gov/public/gsas/.

Thompson, D.E. Cox, and J.B. Hastings. Rietveld refinement of Debye-Scherrer

synchrotron x-ray data from Al2O3, J. Appl. Cryst. 20,79 (1987).

C.J. Howard. The approximation of asymmetric neutron powder diffraction peaks by sums

of Gaussians, J. Appl. Cryst.

15,6

982).

Fundamentals

diffraction

where

and

are tabulated coefficients. Furthermore,

and

is the Gaussian full width at half maximum modified by an

additional broadening parameter,

is Lorentzian full width at half

maximum, which accounts for the anisotropic FWHM behavior by

introducing two anisotropic broadening parameters, X, (crystallite size) and

(strain), and

is the angle between a common anisotropy axis and the

corresponding reciprocal lattice vector.

The major benefit achieved when using the modified pseudo-Voigt

function is in the separation of

FWHM's due to Gaussian and Lorentzian

contributions to the peak shape function. They represent two different effects

contributing to the combined peak width, which are due to the instrumental

(Gauss) and specimen (Lorentz) broadening. The specimen broadening

parameters X and Y, being coefficients of l/cos€l and tang, could be directly

associated with the crystallite size and microstrain, respectively. Anisotropic

broadening can be refined using two additional parameters,

X, and Y,. The

crystallite size

(p)

can be obtained from these parameters as follows:

l8OKh

p. =p

IS0

.nx

and

and microstrain

(s)

in percent as:

180

Chapter

and

(2.60)

where the subscript

iso

indicates isotropic parameters,

and

denote

parameters that are perpendicular and parallel, respectively, to the anisotropy

axis,

is the Scherrer constant,' and

Yh,,

is the instrumental part in the case

of strain broadening.

The third function used in GSAS, is similar to the second function, as

described in Eqs. 2.54

thrrough 2.58. However, it fits real Bragg peak shapes

better due to improved handling of asymmetry, which is treated in terms of

axial di~ergence.~ This function is formed by a convolution of pseudo-Voigt

with the intersection of the diffraction cone and a finite receiving slit length

using two geometrical parameters, S/L and DIL, where S and D are the

sample and the detector slit dimensions in the direction parallel to the

goniometer axis, and L is the goniometer radius. These two parameters can

be measured experimentally or refined when low Bragg angle peaks are

present.

The fourth function is also a modified pseudo-Voigt, but it accounts for

microstrain broadening as suggested by

step hen^.^

Up to 15 coefficients

(in the triclinic crystal system) could be used to describe strain broadening.

Both the third and fourth functions fit asymmetric peaks much better than

the first two and the simple pseudo-Voigt

(Eq.

2.51), especially at low Bragg

angles. The latest function also results in an excellent fit when irregular peak

broadening was caused by microstrains.

the modified pseudo-Voigt functions described above (Eqs. 2.54 to

2.58), both the Gaussian to Lorentzian mixing parameter

(q,

Eq. 2.54) and

their individual contributions to the total peak width

(H,

Eq. 2.55) are

tabulated. This feature may be used to lower the number of free parameters

and to obtain more realistic peak shape parameters that are due to the

physical state of the specimen. Either or both may be achieved by using one

of the following approaches:

is known as the shape factor or Scherrer constant which varies in the range 0.89

and usually

0.9 [H.P. Klug and

L.E.

Alexander, X-ray diffraction procedures for

polycrystalline and amorphous materials, Second edition, John Wiley,

(1974) p.

6561.

L.W.

Finger,

D.E.

Cox, A.P. Jephcoat. A correction for powder diffraction peak

asymmetry due to axial divergence, J. Appl. Cryst.

27,

892 (1994).

P.W. Stephens. Phenomenological model of anisotropic peak broadening in powder

diffraction,

Appl. Cryst. 32,281 (1999).