Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals

diffraction 141

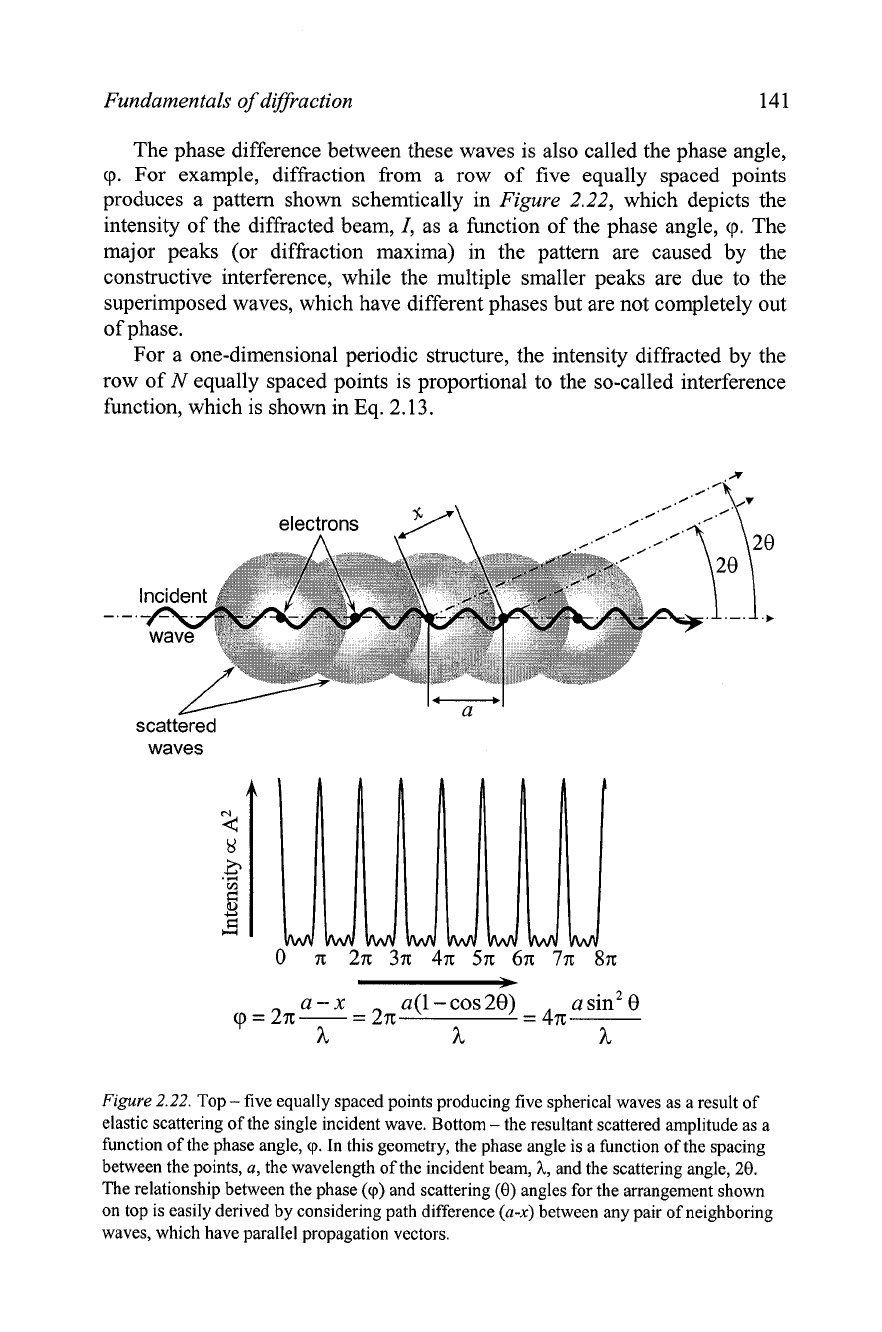
The phase difference between these waves is also called the phase angle,

For example,

diffraction from a row of five equally spaced points

produces a pattern shown schemtically in

Figure

2.22, which depicts the

intensity of the diffracted beam,

as a function of the phase angle,

The

major peaks (or diffi-action maxima) in the pattern are caused by the

constructive interference, while the multiple smaller peaks are due to the

superimposed waves, which have different phases but are not completely out

of phase.

For a one-dimensional periodic structure, the intensity diffracted by the

row of

equally spaced points is proportional to the so-called interference

function, which is shown in

Eq.

2.13.

scattered

waves

a(1-

cos

28)

sin2

2n-

271.

4n-

h h h

Figure

2.22.

Top

five equally spaced points producing five spherical waves as a result of

elastic scattering of the single incident wave. Bottom

the resultant scattered amplitude as a

function of the phase angle,

cp.

In this geometry, the phase angle is a function of the spacing

between the points,

the wavelength of the incident beam,

and the scattering angle,

20.

The relationship between the phase

(cp)

and scattering

(0)

angles for the arrangement shown

on top is easily derived by considering path difference

(a-x)

between any pair of neighboring

waves, which have parallel propagation vectors.

142 Chapter 2

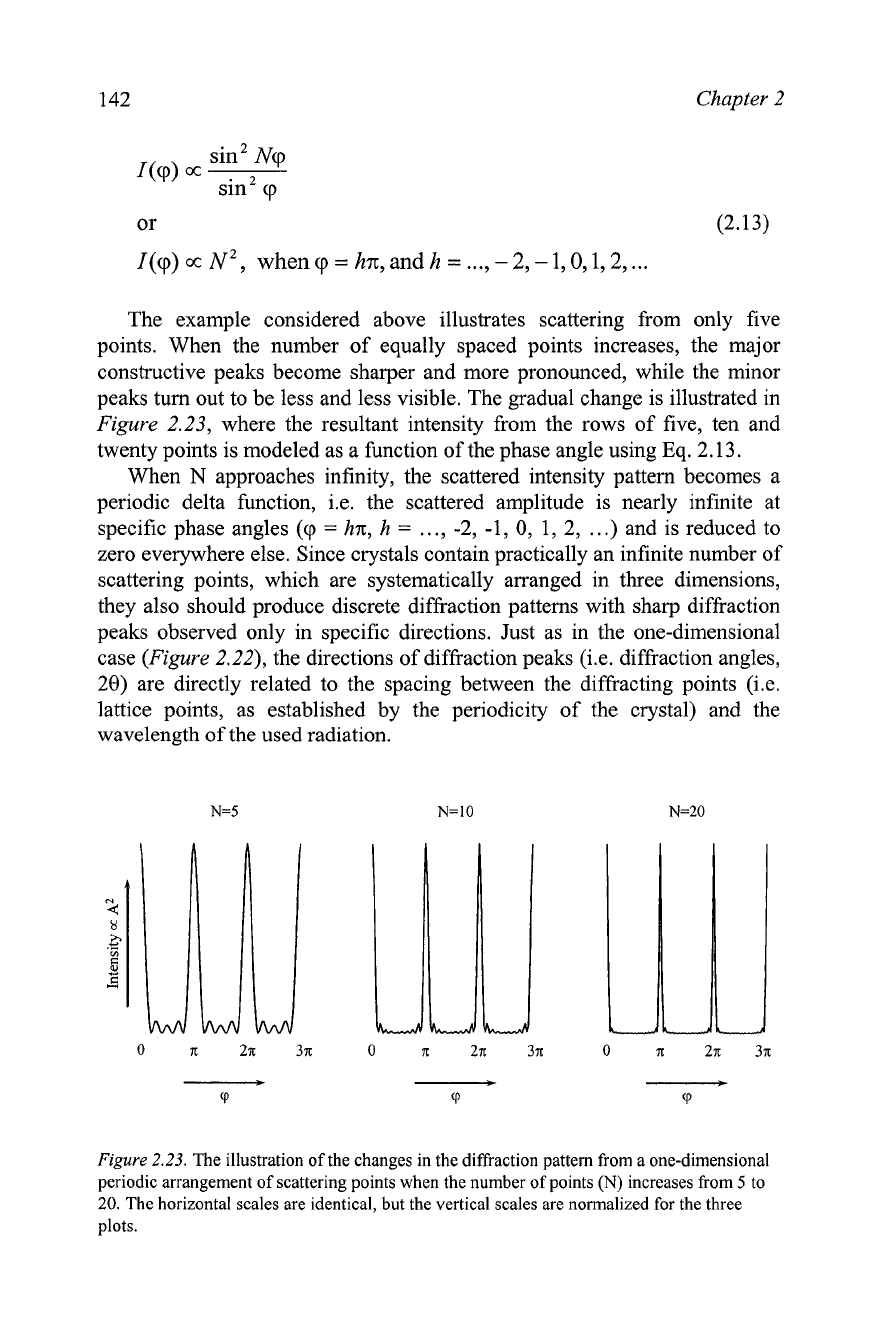
The example considered above illustrates scattering from only five

points. When the number of equally spaced points increases, the major

constructive peaks become sharper and more pronounced, while the minor

peaks turn out to be less and less visible. The gradual change is illustrated in

Figure 2.23, where the resultant intensity from the rows of five, ten and

twenty points is modeled as a function of the phase angle using Eq. 2.13.

When

approaches infinity, the scattered intensity pattern becomes a

periodic delta function, i.e. the scattered amplitude is nearly infinite at

specific phase angles

hn, h

...,

-2, -1,

1, 2,

...)

and is reduced to

zero everywhere else. Since crystals contain practically an infinite number of

scattering points, which are systematically arranged in three dimensions,

they also should produce discrete diffraction patterns with sharp diffraction

peaks observed only in specific directions. Just as in the one-dimensional

case (Figure

2.22), the directions of diffkaction peaks (i.e. diffraction angles,

28) are directly related to the spacing between the diffracting points (i.e.

lattice points, as established by the periodicity of the crystal) and the

wavelength of the used radiation.

Figure

2.23.

The illustration of the changes in the diffraction pattern from a one-dimensional

periodic arrangement of scattering points when the number of points

(N)

increases from

20.

The horizontal scales are identical, but the vertical scales are normalized for the three

plots.

Fundamentals of diffraction

143

2.5.2

Scattering

atoms and scattering factor

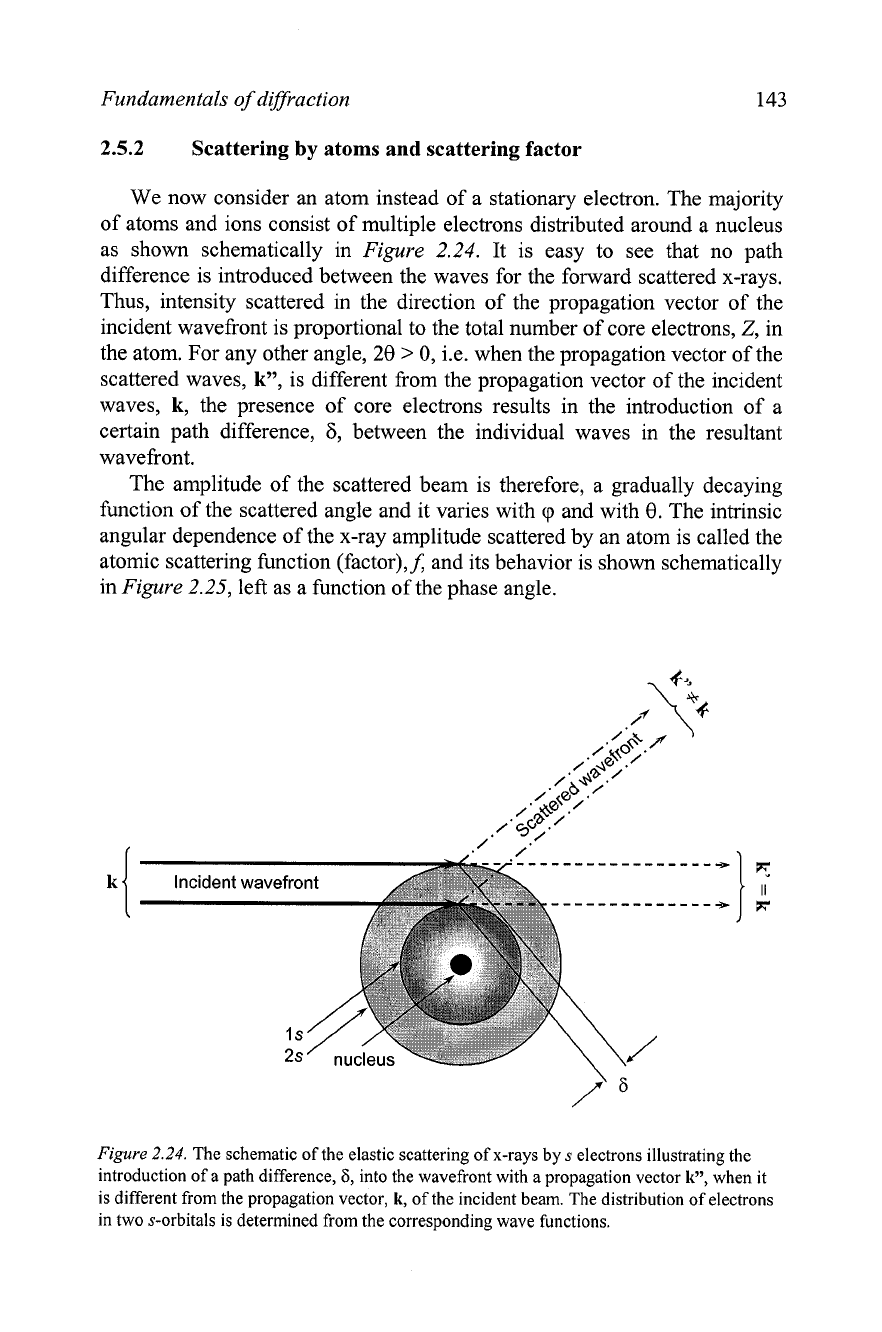
We now consider an atom instead of a stationary electron. The majority

of atoms and ions consist of multiple electrons distributed around a nucleus

as shown schematically in

Figure

2.24. It is easy to see that no path

difference is introduced between the waves for the forward scattered x-rays.

Thus, intensity scattered in the direction of the propagation vector of the

incident wavefiont is proportional to the total number of core electrons,

the atom. For any other angle,

i.e. when the propagation vector of the

scattered waves, k", is different fiom the propagation vector of the incident

waves, k, the presence of core electrons results in the introduction of a

certain path difference,

between the individual waves in the resultant

wave front.

The amplitude of the scattered beam is therefore, a gradually decaying

function of the scattered angle and it varies with

and with

The intrinsic

angular dependence of the x-ray amplitude scattered by an atom is called the

atomic scattering function

(factor),J; and its behavior is shown schematically

Figure

2.25, left as a function of the phase angle.

Figure

2.24.

The schematic of the elastic scattering of x-rays by

electrons illustrating the

introduction of a path difference,

into the wavefront with a propagation vector

k",

when it

is different from the propagation vector,

of the incident beam. The distribution of electrons

in two s-orbitals is determined from the corresponding wave functions.

Chapter

Figure

2.25.

The schematic showing the dependence of the intensity scattered by an atom, i.e.

the atomic scattering factor,

A',

as a function of the phase angle (lefi), and the resultant

decrease of the intensity of the diffraction pattern from the row of five regularly spaced

atoms, also as a function of the phase angle (right).

Thus, when stationary, periodically arranged electrons are substituted by

atoms, their diffraction pattern is the result of a superposition of the two

functions, as shown in

Figure

2.25, right.

other words, the amplitude

squared of the diffraction pattern from a row of

atoms is a product of the

interference function (Eq.

2.13)

and the corresponding atomic scattering

function squared,

2(cp):

It is worth noting that it is the radial distribution of core electrons in an

atom, which is responsible for the reduction of the intensity when the

diffraction angle increases. Thus, it is a specific feature observed in x-ray

diffraction from ordered arrangements of atoms. If, for example, the

diffraction of neutrons is of concern, they are scattered by nuclei, which may

be considered as points. Hence, neutron scattering functions (factors) are

independent of the diffraction angle and they remain constant for a given

type of nuclei (also see

Table

2.2).

Fundamentals

diffraction 145

2.5.3

Scattering

lattices

The interference function in Eq. 2.14 describes a discontinuous

distribution of the scattered intensity in the diffraction space.' Assuming an

infinite number of points in a one-dimensional periodic structure (N

a),

the distribution of the scattered intensity is a periodic delta-function (see

above) and therefore, diffraction peaks occur only in specific points, which

establish a one-dimensional lattice in the diffraction space. Hence, diffracted

intensity is only significant at certain points, which are determined (also see

Eq. 2.13, Figure 2.23, and Figure 2.25) from

three dimensions, a total of three integers

(h,

and

1)2

are required to

define the positions of intensity maxima in the diffraction space:

where

Nl,

and N3 are the total numbers of the identical atoms in the

corresponding directions.

On the other hand, when the unit cell contains more than one atom, the

individual atomic scattering functionflcp) should be replaced with scattering

by the whole unit cell, since the latter is now the object that forms a periodic

array. The scattering function of one unit cell,

is called the structure factor

or the structure amplitude. It accounts for scattering factors of all atoms in

the unit cell together with other relevant atomic parameters. As

result, a

diffraction pattern produced by a crystal lattice may be defined as

sin U,

sin U2kn sin2

U31n

I(cp)

(cp)

sin2

sin2 kn sin2

where U,,

and U3 are the numbers of the unit cells in the corresponding

directions.

The phase angle is a function of lattice spacing (Figure

2.22), which is a

function of

and

As we will see later (section 2.10), the structure factor

Diffraction space, in which diffraction peaks are arranged into a lattice, is identical to a

reciprocal space.

The integers

and

are identical to Miller indices.

146

Chapter

is also a function of the triplet of Miller indices

(hkl).

Hence, in general the

intensities of discrete points

(hkl)

in the reciprocal space are given as

I(hk1)

(hkl)

sin2

U, hn sin2 U2& sin2 U31n

sin2

hn sin2

sin2

The scattered intensity is nearly always measured in relative and not in

absolute units, which necessarily introduces a proportionality coefficient,

As we established before, when the phase angle is nn (n is an integer), the

corresponding interference functions in Eq.

2.18

are reduced to

UI2,

u~~

and

u~~

and they become zero otherwise. Hence, assuming that the volume of a

crystalline material producing a diffraction pattern remains constant (this is

always ensured in a properly arranged experiment), the proportionality

coefficient

can be substituted by a scale factor

CU,~U~~U~~.

addition to the scale factor, intensity scattered by a lattice is also

subject to different geometrical effects,'

which are various functions of

the diffraction angle,

All things considered, the intensity scattered by a

lattice may be given by the following equation:

I(hk1)

G(8)

F2 (hkl)

This is a very general equation for intensity of the individual diffraction

(Bragg) peaks observed in a diffraction pattern of a crystalline substance,

and it will be discussed in details in section 2.10, while the geometry of

powder diffraction, i.e. the directions in which discrete peaks can be

observed, is discussed in the following two sections.

2.6

Geometry of diffraction by lattices

Both direct and reciprocal spaces may be used to understand the

geometry of diffraction by a lattice. Direct space concepts are intuitive, and

therefore, we will begin our consideration using physical space. Conversely,

reciprocal space is extremely useful in the visualization of diffraction

patterns in general and from powders in particular. In this section, therefore,

we also show the relationships between geometrical concepts of diffraction

in physical and reciprocal spaces.

One of these geometrical effects is the polarization factor introduced earlier in the

Thornson's equation, see section

2.5.1

and the corresponding footnote (No.

on page

140).

Fundamentals of diffraction 147

2.6.1

Laue equations and Braggs'

law

The geometry of diffraction from a lattice,

or in other words the

relationships between the directions of the incident and diffracted beams,

was first given by Laue (see the footnote on page 31) in a form of three

simultaneous equations, which are commonly known as Laue equations:

a(cos

cos pl)

b(cosy2 -cosp

)

c(cos

cos g3)

Here a,

and

are the dimensions of the unit cell;

~1-3

and

91-3

are the

angles that the incident and diffracted beams, respectively, form with the

parallel rows of atoms in three independent directions; the three integer

indices

and

have the same meaning as in Eq. 2.18, i.e. they are unique

for each diffraction peak and define the position of the peak in the reciprocal

space (also see Chapter 1, section 1.15), and

is the wavelength of the used

radiation. The cosines, cosy~i and coscpi, are known as the direction cosines of

the incident and diffracted beams, respectively. According to the formulation

given by Laue, sharp diffraction peaks can only be observed when all three

equations in

2.20

are satisfied simultaneously.

Laue equations once again indicate that a periodic lattice produces

diffraction maxima at specific angles, which are defined by both the lattice

repeat distances

(a,

c) and the wavelength

(A).

Laue equations give the

most general representation of a three-dimensional diffraction pattern and

they may be used in the form of Eq. 2.20 to describe the geometry of

diffraction from a single crystal.

More useful in powder diffraction is the law formulated by W.H. Bragg

and W.L. Bragg (see the footnote on page 3 1). It was introduced above (e.g.

see Eq. 2.11) without an explanation, and we already know that it establishes

certain relationships among the diffraction angle (Bragg angle), wavelength

and interplanar spacing.

According to the Braggs, diffraction from a crystalline sample can be

explained and visualized by using a simple notion of mirror reflection of the

incident x-ray beam from a series of crystallographic planes. As established

earlier (see Chapter 1, section

1.14.1), all planes with identical triplets of

Miller indices are parallel to one another and they are equally spaced. Thus,

each plane in a set

(hkl)

may be considered as a separate scattering object.

The set is periodic in the direction perpendicular to the planes and the repeat

distance in this direction is equal to the interplanar distance dhkl. Diffraction

from a set of equally spaced objects is only possible at specific angle(s) as

148 Chapter

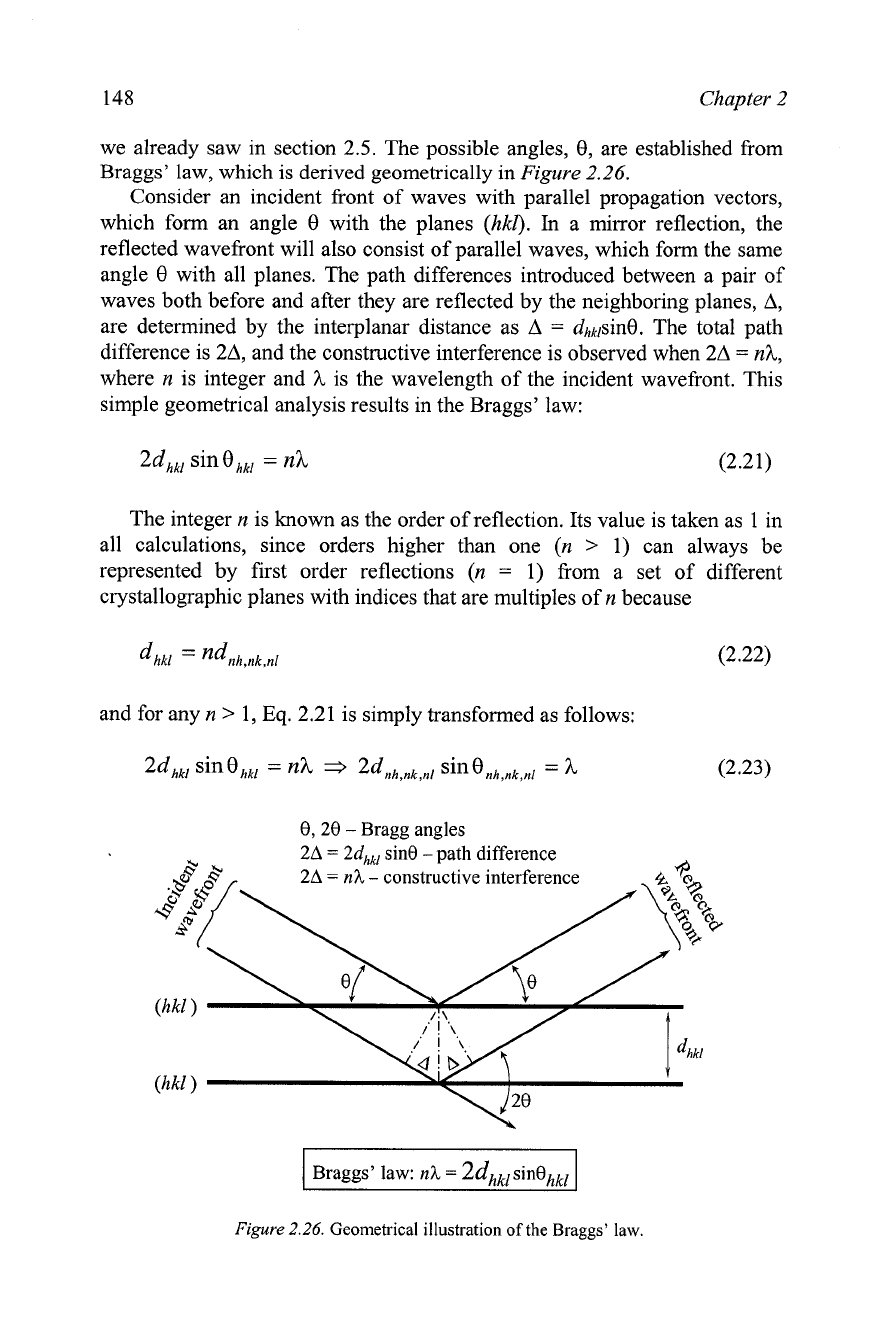
we already saw in section 2.5. The possible angles, 9, are established from

Braggs' law, which is derived geometrically in

Figure

2.26.

Consider an incident front of waves with parallel propagation vectors,

which form an angle 9 with the planes (hkl).

a mirror reflection, the

reflected wavefi-ont will also consist of parallel waves, which form the same

angle 9 with all planes. The path differences introduced between a pair of

waves both before and after they are reflected by the neighboring planes,

are determined by the interplanar distance as

dhklsin9. The total path

difference is 2A, and the constructive interference is observed when 2A

nh,

where n is integer and h is the wavelength of the incident wavefi-ont. This

simple geometrical analysis results in the Braggs' law:

2dj,

sin

The integer n is known as the order of reflection. Its value is taken as 1 in

all calculations, since orders higher than one

1) can always be

represented by first order reflections (n

1) from a set of different

crystallographic planes with indices that are multiples of n because

and for any

Eq.

2.21 is simply transformed as follows:

8,28

Bragg angles

2dj, sin0 -path difference

constructive interference

Braggs' law:

2dhklsinehkl

Figure

2.26.

Geometrical

illustration

the

Braggs'

law.

Fundamentals of diffraction 149

2.6.2

Reciprocal lattice and Ewald's sphere

The better visual representation of the phenomenon of diffraction has

been introduced by Ewald (see the footnote on page 50). Consider an

incident wave with a certain propagation vector, ko, and a wavelength, h. If

the length of

is selected as the inverse of the wavelength

then the entire wave is fully characterized, and it is said that ko is its

wavevector. When the primary wave is scattered elastically, the wavelength

remains constant. Thus, the scattered wave is characterized by a different

wavevector, kl, which has the same length as

k,,:

The angle between

k,,

and k, is 20 (Figure 2.27, left). We now overlap

these two wavevectors with a reciprocal lattice (Figure 2.27, right) such that

the end of

k,-,

coincides with the origin of the lattice. As shown by Ewald,

diffraction in the direction of kl occurs only when its end coincides with a

point in the reciprocal lattice. Thus, considering that

and kl have identical

lengths regardless of the direction of

(the direction of

k,,

is fixed by the

origin of the reciprocal lattice), their ends are equidistant from a common

point and all possible orientations of

delineate a sphere in three

dimensions. This sphere is called the Ewald's sphere, and it is shown

schematically in Figure 2.28. Obviously, the radius of the Ewald's sphere is

llh.

The simple geometrical arrangement of the reciprocal lattice, Ewald's

sphere, and three vectors

(ko, kl, and

d*hW)

in a straightforward and elegant

fashion yields Braggs' equation. From both Figure 2.27 and Figure 2.28, it

is clear that vector kl is a sum of two vectors,

and

d*hkl:

Its length is known (llh) and its orientation, i.e. angle 0, is found by a

simple algebraic transformation after recalling that

ld*~

lld:

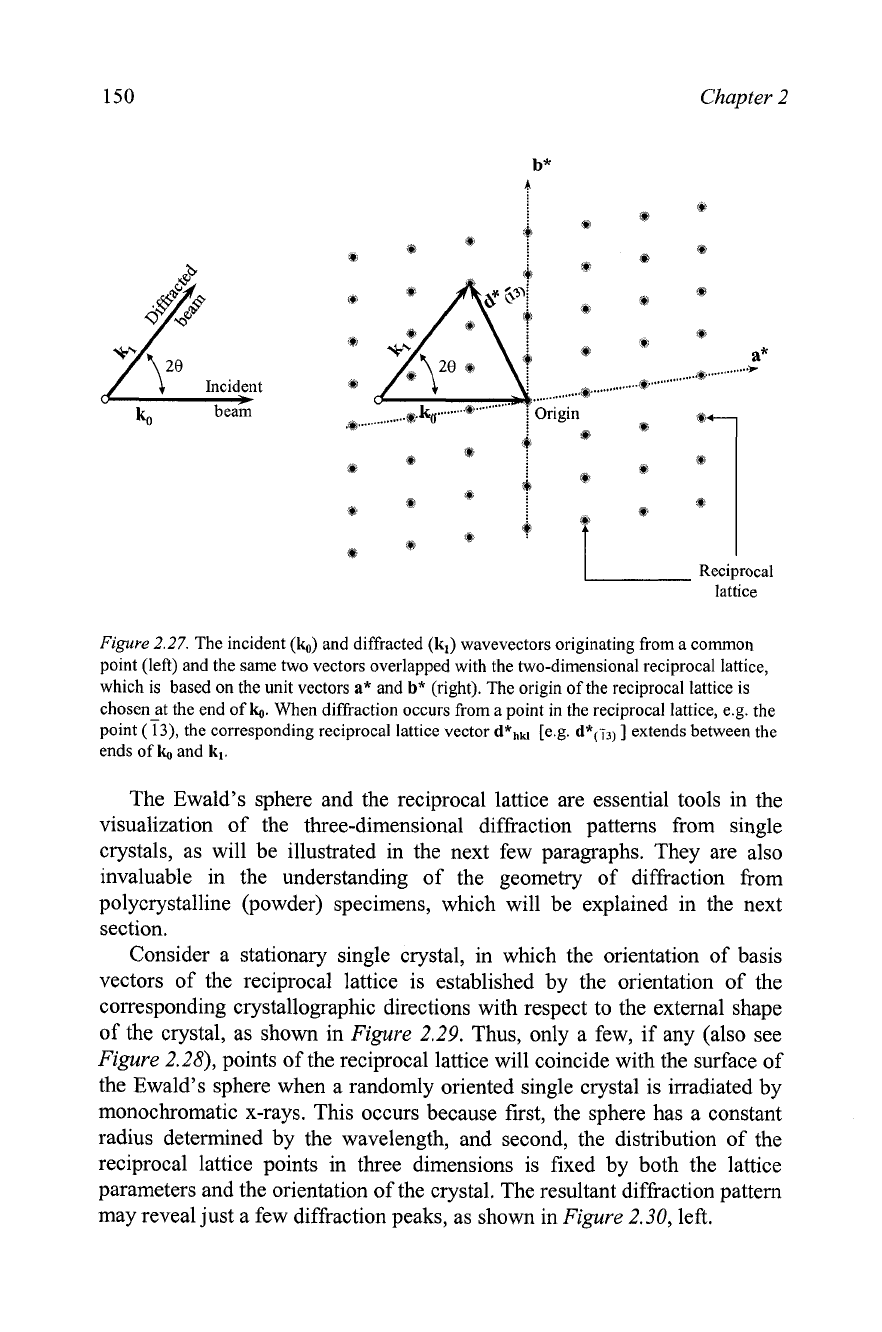
Chapter

Incident

beam

Reciprocal

lattice

Figure

2.27.

The incident

(k,,)

and diffracted

(k,)

wavevectors originating from a common

point (left) and the same two vectors overlapped with the two-dimensional reciprocal lattice,

which is based on the unit vectors

and

(right). The origin of the reciprocal lattice is

chosen at the end of

k,,.

When diffraction occurs from a point in the reciprocal lattice, e.g. the

point

(i3),

the corresponding reciprocal lattice vector

d*hkl

[e.g.

d*(i3)

]

extends between the

ends of

and

k,.

The Ewald's sphere and the reciprocal lattice are essential tools in the

visualization of the three-dimensional diffraction patterns from single

crystals, as will be illustrated in the next few paragraphs. They are also

invaluable in the understanding of the geometry of diffraction from

polycrystalline (powder) specimens, which will be explained in the next

section.

Consider a stationary single crystal, in which the orientation of basis

vectors of the reciprocal lattice is established by the orientation of the

corresponding crystallographic directions with respect to the external shape

of the crystal, as shown in

Figure

2.29. Thus, only a few, if any (also see

Figure

2.28), points of the reciprocal lattice will coincide with the surface of

the Ewald's sphere when a randomly oriented single crystal is irradiated by

monochromatic x-rays. This occurs because first, the sphere has a constant

radius determined by the wavelength, and second, the distribution of the

reciprocal lattice points in three dimensions is fixed by both the lattice

parameters and the orientation of the crystal. The resultant diffraction pattern

may reveal just a few diffraction peaks, as shown in

Figure

2.30, left.