Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Fundamentals of diffvaction

161

2.7.2

Understanding of powder diffraction patterns

The best way to appreciate and understand how structural information is

encoded in a powder diffraction pattern is to consider the latter as a set of

discrete diffraction peaks (Bragg reflections) superimposed over a

continuous background. Although the background may be used to extract

information about the crystallinity of the specimen and few other parameters

about the material, we will be concerned with the Bragg peaks and not with

the background.

the majority of powder diffraction applications the

background is an inconvenience, which has to be dealt with, and generally

every attempt is made to achieve its minimization during the experiment.

Disregarding the background, the structure of a typical powder

diffraction pattern may be described by the following components:

positions,

intensities

and

shapes

of multiple Bragg reflections, e.g. compare

Figure

2.36a and

Figure

2.37a. Each of the three components italicized above

contains information about the crystal structure of the material, the

properties of the specimen (sample) and the instrumental parameters, as

shown in

Table

2.7. Some of these parameters have the key role in defining a

particular component of the powder diffraction pattern, while others result in

various distortion(s) as also indicted in

Table

2.7. It is worth noting that this

table is not comprehensive and additional parameters may affect positions,

intensities and shapes of Bragg peaks.

Table

2.7.

Powder diffraction pattern as a function of various crystal structure, specimen and

instrumental parametersa

Pattern Crystal Specimen Instrumental

component structure property parameter

Unit cell

Absorption

Radiation (wavelength)

parameters:

Porosity

Instrument/sample alignment

Axial divergence of the beam

Atomic

Preferred orientation

Geometry and configuration

parameters

Absorption

Radiation (Lorentz,

(x,

y, z,

etc.)

Porosity

polarization)

Crystallinity Grain size

Radiation (spectral purity)

Strain

Geometry

Defects

Stress

Beam conditioning

Key parameters are shown in

bold.

Parameters that may have a significant influence are

shown in

italic.

addition to the influence brought about by the instrumental parameters,

there are two kinds of crystallographic (structural) parameters, which

essentially define the structure of every powder diffraction pattern. These are

the unit cell dimensions and the atomic structure (both the unit cell content

and spatial distributions of atoms in the unit cell). Thus, a powder diffraction

pattern can be constructed (or simulated) as follows:

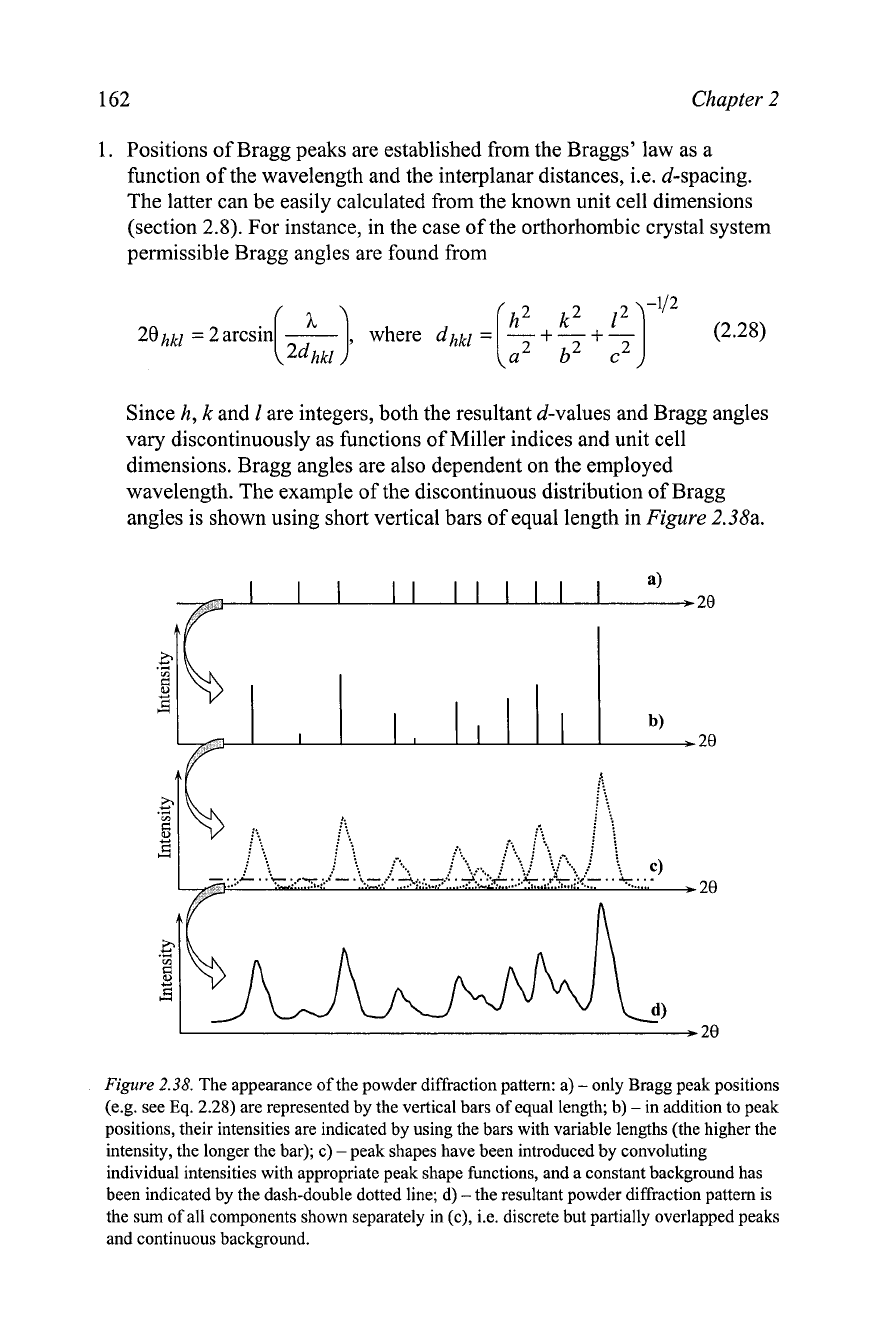
162

Chapter

Positions of Bragg peaks are established from the Braggs' law as a

function of the wavelength and the interplanar distances, i.e. d-spacing.

The latter can be easily calculated from the known unit cell dimensions

(section 2.8). For instance, in the case of the orthorhombic crystal system

permissible Bragg angles are found from

(h:

':)112

(2.28)

hk1

2 arcsin[&), wee dhkl

Since h,

and

are integers, both the resultant d-values and Bragg angles

vary discontinuously as functions of Miller indices and unit cell

dimensions. Bragg angles are also dependent on the employed

wavelength. The example of the discontinuous distribution of Bragg

angles is shown using short vertical bars of equal length in

Figure

2.38a.

Figure

2.38.

The appearance of the powder diffraction pattern: a)

only Bragg peak positions

(e.g. see Eq. 2.28) are represented by the vertical bars of equal length; b)

in addition to peak

positions, their intensities are indicated by using the bars with variable lengths (the higher the

intensity, the longer the bar); c) -peak shapes have been introduced by convoluting

individual intensities with appropriate peak shape functions, and a constant background has

been indicated by the dash-double dotted line; d) -the resultant powder diffraction pattern is

the sum of all components shown separately in (c), i.e. discrete but partially overlapped peaks

and continuous background.

Fundamentals of diffvaction

163

As noted in section

2.5,

the intensity of diffraction maxima is a function

of the periodicity of the scattering ;enters (unit cells) and therefore, the

intensities can be calculated for individual Bragg peaks from the structural

model. The latter requires the knowledge of the coordinates of atoms in

the unit cell together with other relevant atomic and geometrical

parameters. The influence of the varying intensity on the formation of the

powder diffraction pattern is illustrated using the varying lengths of the

bars in

Figure

2.38b

the longer the bar, the higher the intensity.

Although not shown in

Figure

2.38, certain combinations of Miller

indices may have zero or negligibly small intensity and, therefore, the

corresponding Bragg reflections disappear or become unrecognizable in

the diffraction pattern.

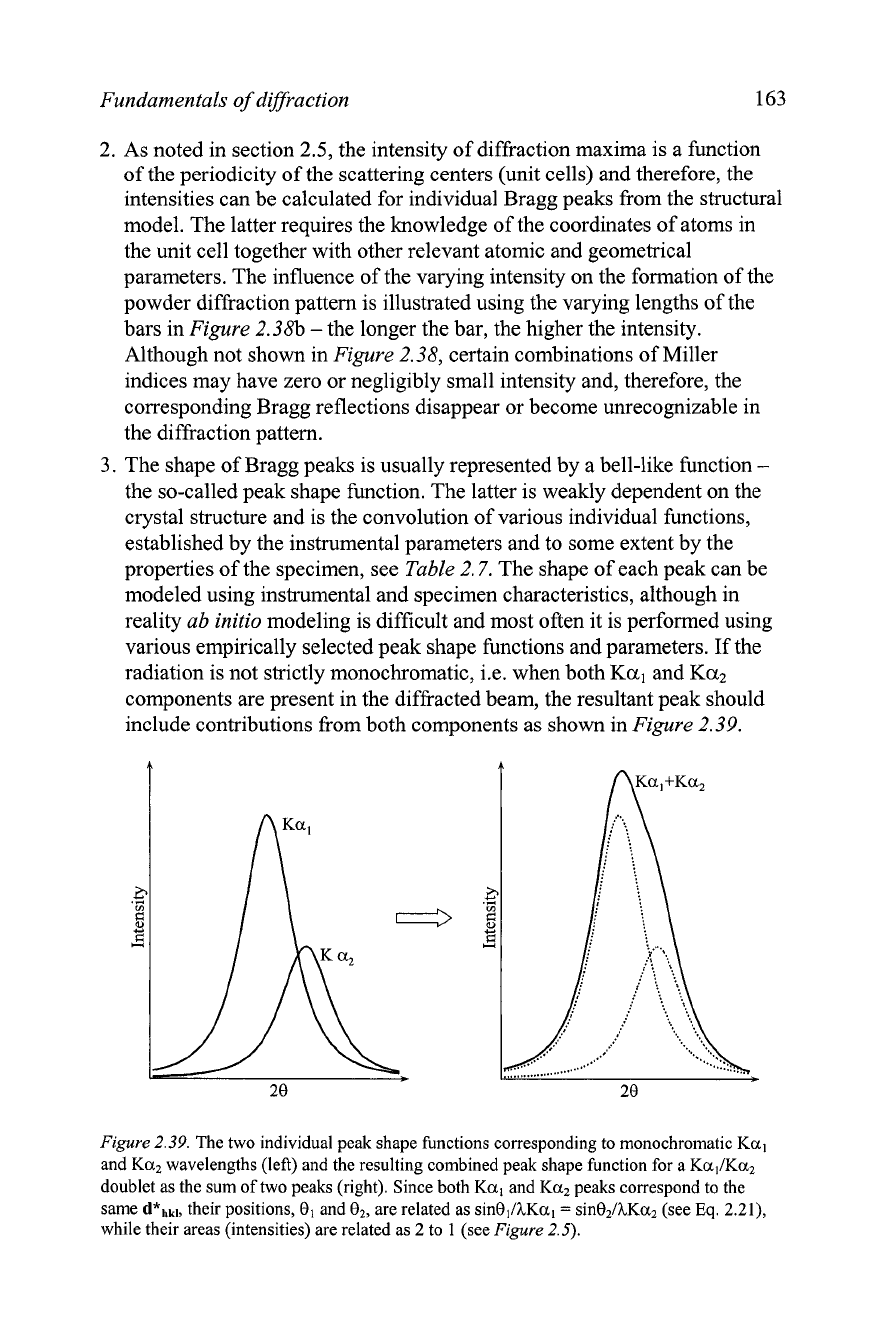
The shape of Bragg peaks is usually represented by a bell-like function

the so-called peak shape function. The latter is weakly dependent on the

crystal structure and is the convolution of various individual functions,

established by the instrumental parameters and to some extent by the

properties of the specimen, see

Table

2.7. The shape of each peak can be

modeled using instrumental and specimen characteristics, although in

reality

ab initio

modeling is difficult and most often it is performed using

various empirically selected peak shape functions and parameters. If the

radiation is not strictly monochromatic, i.e. when both

Ka,

and

Ka2

components are present in the diffi-acted beam, the resultant peak should

include contributions from both components as shown in

Figure

2.39.

Figure

2.39. The two individual peak shape functions corresponding to monochromatic Kal

and Ka2 wavelengths (left) and the resulting combined peak shape function for a KaIIKa2

doublet as the sum of two peaks (right). Since both Ka, and Ka2 peaks correspond to the

same d*hkl, their positions, 0, and 02, are related as sinO,lhKal

~in0~lhKa~ (see

Eq.

2.21),

while their areas (intensities) are related as

(see

Figure

2.5).

164 Chapter 2

Thus, vertical bars with different lengths are replaced by the

corresponding peak shape functions, as shown in

Figure

2.38~. It should

be noted that although the relative intensities of different Bragg

reflections may be adequately represented by the lengths of the bars, this

is no longer correct for peak heights: the bars are one-dimensional and

have zero area, but peak area is a function of the full width at half

maximum, which varies with Bragg angle. Individual peaks should have

their areas proportional to intensities of individual Bragg reflections (see

section 2.10.1).

4. Finally, the resultant powder diffraction pattern is a sum of the individual

peak shape functions and a background function as illustrated in

Figure

2.38d, where the background function was assumed constant for clarity.

It is generally quite easy to simulate the powder diffraction pattern when

the crystal structure of the material is known (the peak shape parameters are

empirical and the background, typical for a given instrument, may be

measured). The inverse process, i.e. the determination of the crystal structure

from powder diffraction data is much more complex. First, individual Bragg

peaks should be located on the pattern, and both their positions and

intensities determined by fitting to a certain peak shape function, including

the background. Second, peak positions are used to establish the unit cell

symmetry, parameters and content. Third, peak intensities are used to

determine space group symmetry and coordinates of atoms. Fourth, the

entire diffraction pattern is used to refine all crystallographic and peak shape

function parameters, including the background. All these issues will

discussed and illustrated in Chapters

through

2.8

Positions of powder diffraction peaks

As was discussed earlier in general terms, diffraction peaks appear at

specific angles due to scattering by periodic lattices. Furthermore, as shown

by the Braggs and confirmed by Ewald (section

2.6), these angles are a

discontinuous function of the interplanar distances (lengths of independent

reciprocal lattice vectors) and the wavelength (radius of the Ewald's sphere).

Therefore, both the unit cell dimensions and the wavelength are the two

major factors that determine Bragg angles. As we will also see below, the

observed peak positions can be distorted by instrumental and specimen

parameters.

2.8.1

Peak positions as a function of unit cell dimensions

The interplanar distance is a function of the unit cell parameters and

Miller indices, h,

and

which fully describe every set of crystallographic

Fundamentals

diffraction

165

planes. The corresponding formulae for the inverse square of the interplanar

distance, lld2, are usually given separately for each crystal system,' as shown

in Eqs. 2.29 to 2.34.

Cubic:

h2+k2+12

h2+k2

Tetragonal:

4h2+hk+k2

Hexagonal:

h2 k2

Orthorhombic:

dabc

Monoclinic:

h k

2hl cos

+,+

(2.33)

a2sin2p

c2sin2p acsin2p

Triclinic:

Primitive rhombohedral lattices, i.e, when

and

90"

are nearly always

treated in the hexagonal basis with rhombohedral

(R)

lattice centering. In a primitive

rhombohedral lattice

(h2

12)sin2

2(hk

hl)(cos2

cosa)

a2(1

3cos2

2cos3 a)

166 Chapter

The most complex formula is the one for the triclinic crystal system, in

which a total of six independent parameters are required to describe the unit

cell dimensions. On the other hand, Eq. 2.34 is the most general, since Eqs.

2.29 to 2.33 are easily derived fi-om it. For example, after introducing the

corresponding relationships between the unit cell dimensions for the

tetragonal crystal system

(i.e. a

90") into Eq. 2.34, the

latter is straightforwardly simplified to Eq. 2.30. The simplified formulae are

only useful in manual calculations but when the list of possible d's (or 8's) is

generated using a computer program, it makes much more sense to employ

only the most general equation since obviously the resultant lld2 values will

be correct upon the substitution of the appropriate numerical values into

Eq. 2.34.

The usefulness of the reciprocal lattice concept may be once again

demonstrated here by illustrating how easily Eqs. 2.29 to 2.34 can be derived

in the reciprocal space employing reciprocal lattice vectors. When the

derivation is performed in the direct space the geometrical considerations

become quite complex.

Consider a reciprocal lattice as shown schematically in Figure

2.40.

Any

reciprocal lattice vector, dJ'hkl, is a sum of three non-coplanar vectors (a*, b*

and

are the unit vectors of the reciprocal lattice and h,

and

are

integers):

For example, in the orthorhombic crystal system

90".

Hence, Eq. 2.35 is transformed into

*,,

(ha

*)'

(kb

*)'

(lc

*)'

and Eq. 2.32 is obtained immediately because d*

lld, a*

lla, b*

llb

and a*

llc.

In the general case (triclinic crystal system), the equivalent of Eq. 2.36 is

more complex

d *2

h2a

+k2b *2 +12c *2

2hka

cosy

+2hla

cos

+2klb

cos

(2.37)

but it becomes considerably more intuitive and easier to understand in terms

of reciprocal lattice parameters than Eq. 2.34, which is given in terms of

direct unit cell dimensions.

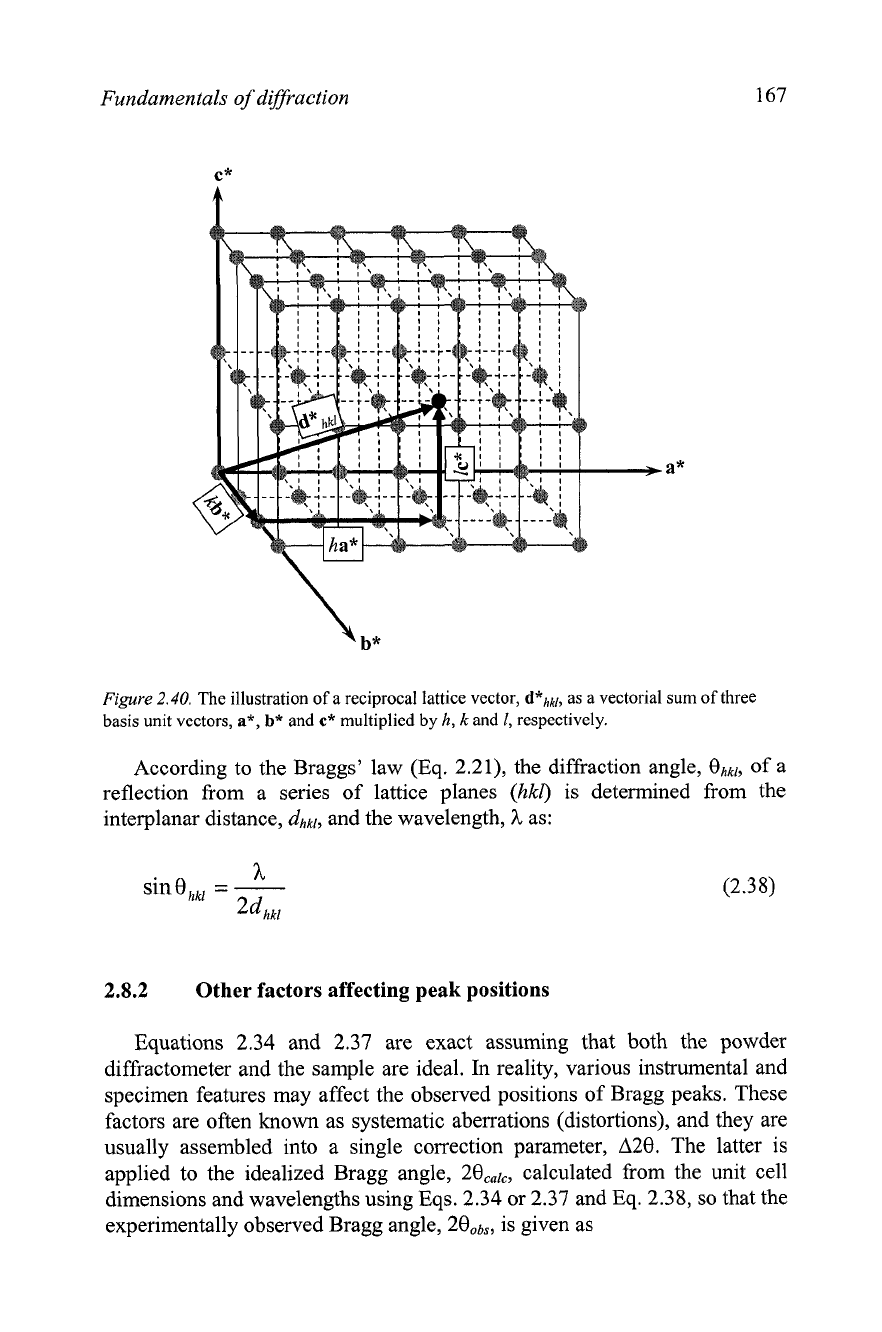
Fundamentals of diffraction

Figure

2.40.

The illustration of a reciprocal lattice vector,

dxhkl,

vectorial sum of three

basis unit vectors,

a*,

and

multiplied by

and

respectively.

According to the Braggs' law (Eq. 2.21)' the diffraction angle, ehkl, of a

reflection from a series of lattice planes

(hkl)

is determined from the

interplanar distance, dhkl, and the wavelength,

as:

sine,,

2dhkl

2.8.2

Other factors affecting peak positions

Equations 2.34 and 2.37 are exact assuming that both the powder

diffractometer and the sample are ideal. In reality, various instrumental and

specimen features may affect the observed positions of Bragg peaks. These

factors are often known as systematic aberrations (distortions), and they are

usually assembled into a single correction parameter, A29. The latter is

applied to the idealized Bragg angle, 29,,lc, calculated from the unit cell

dimensions and wavelengths using Eqs. 2.34 or 2.37 and

Eq.

2.38, so that the

experimentally observed Bragg angle, 2Oob,, is given as

168 Chapter

For the most commonly used Bragg-Brentano focusing geometry (see

Chapter

3),

the overall correction is generally a sum of six factors:

A28

+~+~+p,sin28+p,cos~+p,

tan 28 sin28 tan8

The first two parameters,

and p2, account for the axial divergence of

the incident beam and they can be expressed as

where h is the length of the specimen parallel to the goniometer axis,

is the

goniometer radius,

and K2 are constants established by the collimator.

Soller slits usually minimize the axial divergence and therefore, these two

corrections are often neglected for practical purposes.

addition to axial divergence, the first parameter

(pl)

includes a shift

that is due to peak asymmetry caused by other factors. One of these is the

finite length of the receiving slit of the detector, which results in the

measurement of a fixed length of an arc (see Figure

2.34)

rather than an

infinitesimal point of the Debye ring. The curvature of the Debye ring

increases' with the decreasing Bragg angle and the resultant increasing peak

asymmetry cannot be corrected for by using Soller slits. This effect can be

minimized by reducing the detector slit length, which however, considerably

lowers the measured intensity.

The third parameter,

p3, is given as

Strictly speaking, the curvature of the Debye ring increases both below and above 20

90•‹, e.g. see

Figure

2.32.

Both the curvature and associated asymmetry become especially

significant when 20

-20" and 20

-160". At low Bragg angles this contribution to

asymmetry results in the enhancement of the low angle slopes of Bragg peaks, while at

high Bragg angles the asymmetry effect is opposite. Asymmetry at high Bragg angles is

often neglected because the intensity of Bragg peaks is usually low due to a variety of

geometrical and structural factors, which will be discussed in sections 2.10 and 2.1 1. It is

also worth mentioning that at 20

90" the contribution from

becomes negligible

because tan20

oo.

Fundamentals of diffraction

where

is the in-plane divergence of the x-ray beam and

is a constant.

This factor accounts for the zero curvature of flat samples, typically used in

Bragg-Brentano goniometers. This geometry of the sample distorts the ideal

focusing in which the curvature of the sample surface should vary with

Bragg angle. The aberrations are generally insignificant and they are usually

neglected in routine powder

diffkaction experiments.

The fourth parameter is

where

pef is the effective linear absorption coefficient. This correction is

known as the transparency shift error and it may play a role when examining

thick (more than 50 to 100 pm) samples. The transparency shift error is

caused by the penetration of the beam into the sample and the penetration

depth is a function of Bragg angle. Usually

is the refined parameter since

peff is rarely known (both the porosity and the density of the powder sample

are usually unknown). The transparency shift error could be substantial for

low absorbing samples,

e.g. organic compounds, and it is usually negligible

for highly absorbing specimens, i.e. compounds containing heavy chemical

elements. For low absorbing materials this shift can be reduced by using thin

samples, however, doing so significantly decreases intensity at high Bragg

angles. The latter is already small when a compound consists of light

chemical elements due to their low x-ray scattering ability.

The fifth parameter characterizes specimen displacement, s, from the

goniometer axis and it is expressed as

where

is the radius of the goniometer. This correction may be substantial,

especially when there is no good and easy way to control the exact position

of the specimen surface.

The last parameter, p6, is constant over the whole range of Bragg angles

and the corresponding aberration usually arises due to improper setting(s) of

zero angles for one or more diffractometer axes: detector and/or x-ray

source. Hence, this distortion is called the zero shift error. The zero shift

error can be easily minimized by proper alignment of the goniometer.

However, in some cases,

e.g. in neutron powder diffraction, zero shift is

practically unavoidable and, therefore, should be always accounted for.

In routine experiments most or even all peak displacement corrections

(Eq.

2.40) may be ignored when their effect falls into the range of

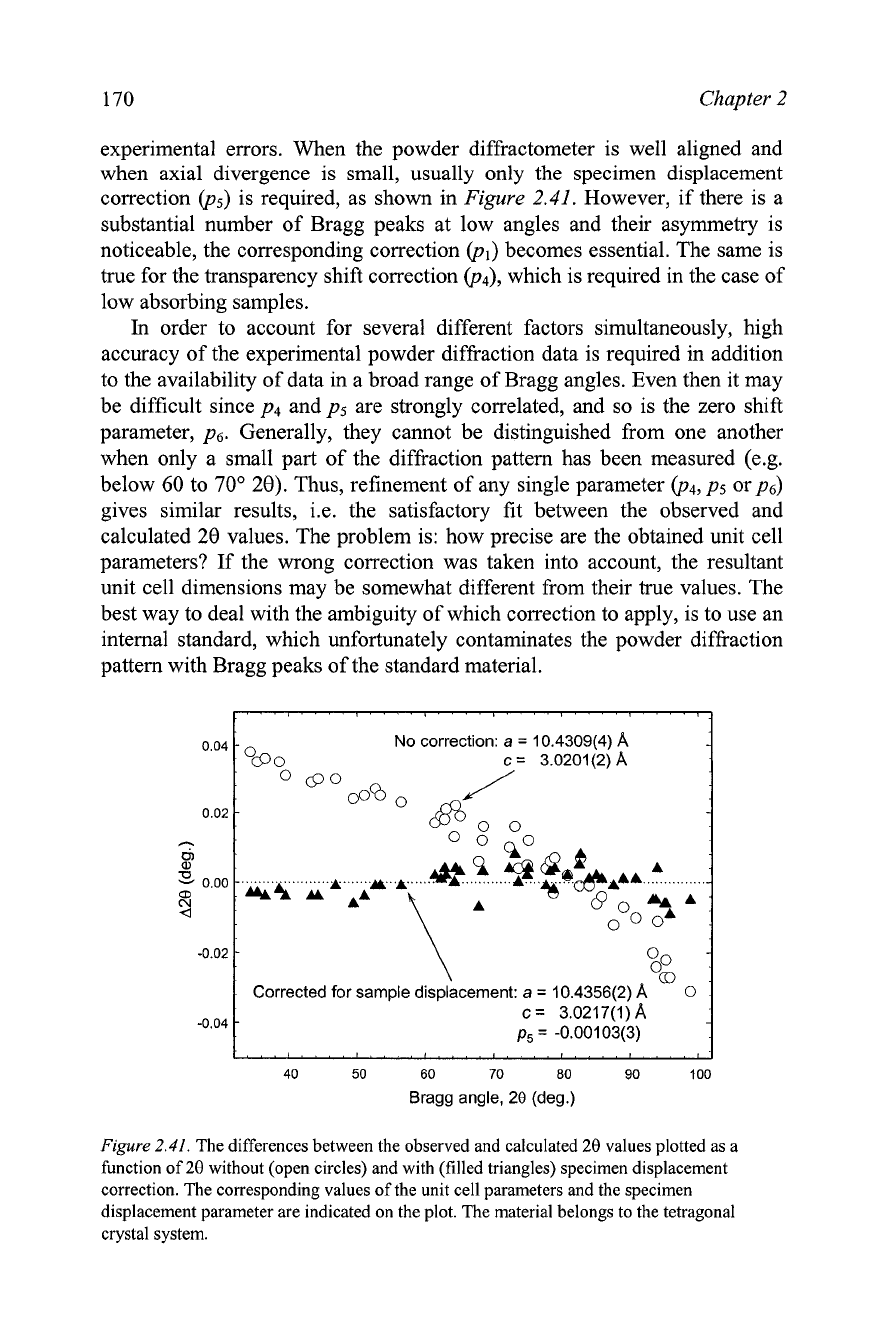
170 Chapter

experimental errors. When the powder diffractometer is well aligned and

when axial divergence is small, usually only the specimen displacement

correction (p5) is required, as shown in Figure

2.41.

However, if there is a

substantial number of Bragg peaks at low angles and their asymmetry is

noticeable, the corresponding correction

(p,)

becomes essential. The same is

true for the transparency shift correction (p4), which is required in the case of

low absorbing samples.

order to account for several different factors simultaneously, high

accuracy of the experimental powder diffraction data is required in addition

to the availability of data in a broad range of Bragg angles. Even then it may

be difficult since

and

are strongly correlated, and so is the zero shift

parameter, P6. Generally, they cannot be distinguished from one another

when only a small part of the diffraction pattern has been measured (e.g.

below

70'

20). Thus, refinement of any single parameter

(p4,

or ~6)

gives similar results, i.e. the satisfactory fit between the observed and

calculated 20 values. The problem is: how precise are the obtained unit cell

parameters? If the wrong correction was taken into account, the resultant

unit cell dimensions may be somewhat different from their true values. The

best way to deal with the ambiguity of which correction to apply, is to use an

internal standard, which unfortunately contaminates the powder diffraction

pattern with Bragg peaks of the standard material.

Figure

2.41.

The differences between the observed and calculated

values plotted as a

function of

without (open circles) and with (filled triangles) specimen displacement

correction. The corresponding values of the unit cell parameters and the specimen

displacement parameter are indicated on the plot. The material belongs to the tetragonal

crystal system.

0.04

0.02

No correction:

10.4309(4)

OSO

3.0201(2)

00%

oooA

-0.02

o",

-0.04

Corrected for sample displacement:

10.4356(2)

3.02Ii'(l)

-0.00103(3)

,....

I....,.,..,,.,.,

40 50 60 70 80 90 100

Bragg angle, 28 (deg.)