Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Chapter

The first one is symbolic, and it is used to simplify written descriptions of

symmetry.

The second method is algebraic, and it is very convenient in manipulating

symmetry.

begin with the symbolic description of symmetry operations, which

is based on the fact that the action of any symmetry operation or any

combination of symmetry operations can be described by the coordinates of

the resulting

object(s). In this section we assume that the initial object has

coordinates x, y, z.

1.19.1

Finite symmetry operations

Consider a mirror plane that is perpendicular to the Z-axis and intersects

with this axis at the origin (z

0). This plane will reflect objects leaving

their x and y coordinates unchanged but the z coordinate of the initial object

would be inverted and will become

-z

after the reflection operation is

performed. Therefore, the symbolic description of this mirror reflection

operation is x, y,

-z.

Another example to consider, are four symmetry operations in the point

group symmetry 2lm as depicted in

Figure

1.46.

The coordinates of four symmetrically equivalent points in

Figure

1.46

fully characterize all performed symmetry operations. Beginning from point

The one-fold rotation converts the object into itself

A),

which

results in x, y, z.

The center of symmetry inverts all three coordinates of the object in the

point with coordinates

0, 0

D),

which results in -x, -y, -z.

Figure

1.46.

Symmetry elements and symbolic description of symmetry operations in the

point group symmetry 2lm. Here, the origin of the coordinate system coincides with the center

of inversion.

Fundamentals

crystalline state

The mirror plane perpendicular to the Y-axis inverts y leaving x and z

unchanged

C),

which results in x, -y, z.

The two-fold rotation axis parallel to

inverts both x and z leaving y

unchanged (A

B),

which results in -x, y, -z.

Therefore, zero, one, two or all three coordinates change their signs, but

this only holds for symmetry elements of the first and second order when

they are aligned with one of the three major crystallographic axes. Symmetry

operations describing both diagonal symmetry elements and symmetry

elements with higher order

(i.e. three-, four- and six-fold rotations) may

cause permutations and more complex relationships between the coordinates.

For example:

Reflection in the diagonal mirror plane may be symbolically described as

x, z.

Rotations around the six-fold rotation axis parallel to

result in x-y, x, z;

y, -x+y, z; -x, -y, z; -x+y, -x, z; and -y, x-y, z.'

Symmetry operations due to the presence of the three-fold rotation axis

along the body diagonal of a cube in the [I 111 direction are described by

Z, X, y and y, z, x.

1.19.2

Infinite symmetry operations

All examples considered above illustrate symmetry elements that traverse

the origin of coordinates and do not have translations. When symmetry

elements do not intersect the origin

(0,0,0) or have translations (e.g. glide

planes and screw axes), their symbolic description includes fractions of full

translations along the corresponding crystallographic axes. For example:

Reflection in the mirror plane perpendicular to

that intersects the Z-axis

at z

0.25 is described as x,

112-2 (or x, y, -z+112).

Rotation around and corresponding translation along the two-fold screw

axis, which coincides with

results in -x, 1/2+y, -2.

Reflection in the glide plane, n, perpendicular to

and intersecting

0.25 is described symbolically as 112-x, 112+y, 112+2.

The non-primitive translation in the base-centered unit cell C yields

x+1/2, y+1/2, z.

This description formalizes symmetry operations by using the

coordinates of the resulting points and, therefore, it is broadly used to

represent both symmetry operations and equivalent positions in the

International Tables for Crystallography (see

Table

1.18).

The symbolic

description of symmetry operations, however, is not formal enough to enable

easy manipulations involving crystallographic symmetry operations.

In a crystallographic basis where

X-

and Y-axes form a

120'

angle between them, and

Z-

axis is perpendicular

both

and Y.

Chapter

1.20

Algebraic treatment of symmetry operations

Earlier (see

Figure

1.7) we established that there are four simple

symmetry operations, namely: rotation, reflection, inversion and translation.

Among the four, reflection in a mirror plane may be represented as a

complex symmetry element

two-fold inversion axis

which includes

simultaneous two-fold rotation and inversion. Therefore, in order to

minimize the number of simple symmetry operations, we will begin with

rotation, inversion and translation, noting that complex operations can be

described as simultaneous applications of these three simple transformations.

Algebraic description of symmetry operations is based on the following

simple notion. Consider a point in a three-dimensional coordinate system

with any (not necessarily orthogonal) basis, which has coordinates x, y, z.

This point can be conveniently represented by the coordinates of the end of

the vector, which begins in the origin of the coordinates

0, 0, 0 and ends at

x, y, z. Thus, one only needs to specify the coordinates of the end of this

vector in order to fully characterize the location of the point. Any

symmetrical transformation of the point, therefore, can be described by the

change in either or both the orientation and the length of this vector.

1.20.1

Transformations of coordinates of

point

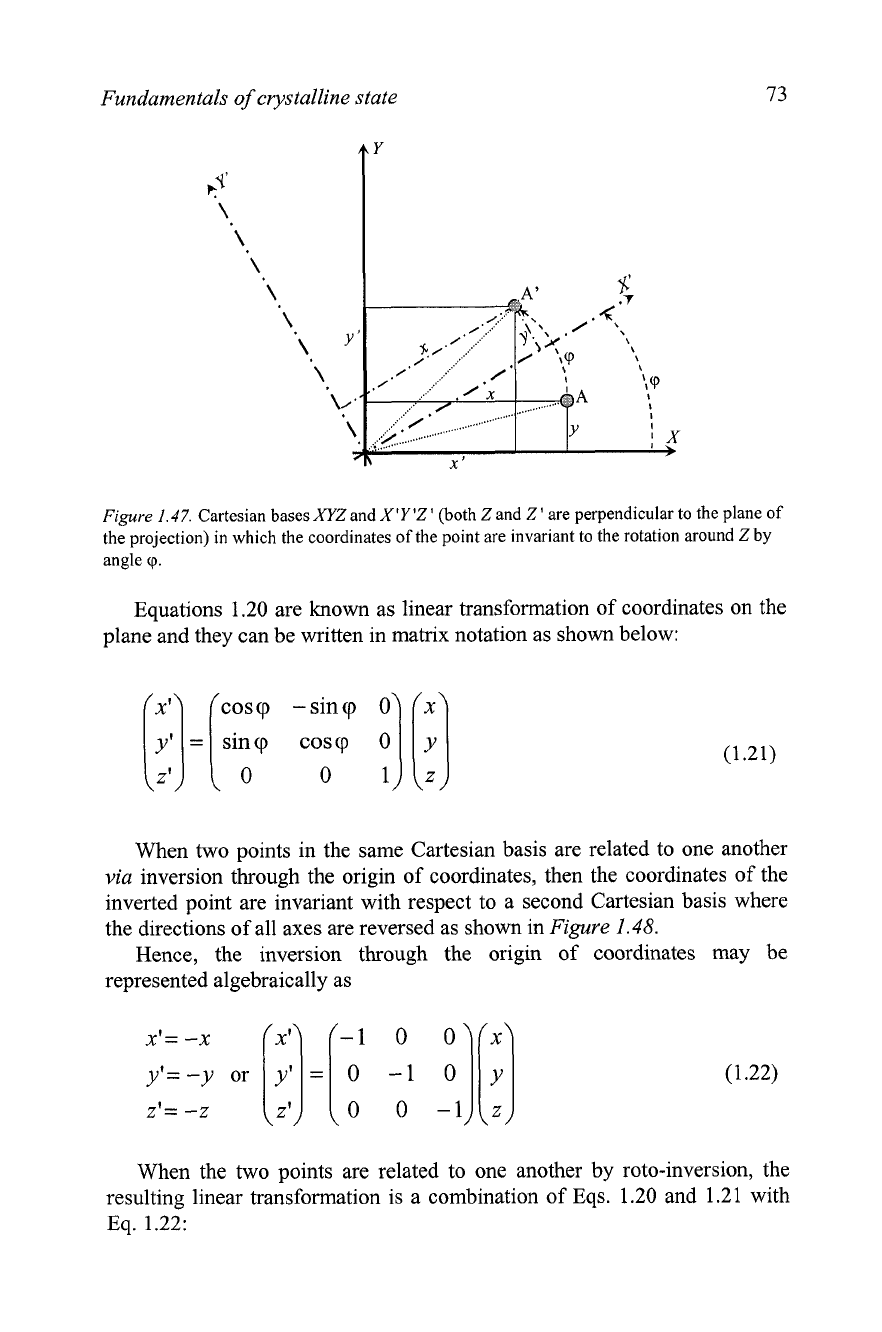
Consider point A with coordinates x, y,

in a Cartesiani basis

XYZ.

Also,

consider point A' with coordinates

x',

y',

in the same basis, which is

obtained from point A by rotating it around

by angle

cp.

It is worth noting

that since orientations of rotation axes in crystallography are restricted, e.g.

see

Table

1.8, we may limit our analysis to rotations about one of the basis

axes.

As shown in

Figure

1.47, it is possible to select a different Cartesian

basis,

ZYZ',

which is related to the original basis,

XYZ,

by the identical

rotation around

and in which the coordinates of the point A' will be x, y, z,

i.e. they are invariant to this transformation of coordinates. From the

schematic shown in

Figure

1.47 it is easy to establish that the rotational

relationships between the coordinate triplets x, y, z and x', y', z' in the original

basis

XYZ

are given as

x'= xcoscp- ysincp

yl= xsincp+ ycoscp

Cartesian coordinate system

(or

basis) is the orthogonal system with

and

a=p=y=90•‹.

Fundamentals

crystalline state

Figure

1.47.

Cartesian bases

XYZ

and

(both

and

are perpendicular to the plane of

the projection) in which the coordinates of the point are invariant to the rotation around

angle

cp.

Equations 1.20 are known as linear transformation of coordinates on the

plane and they can be written in matrix notation as shown below:

coscp -sin9

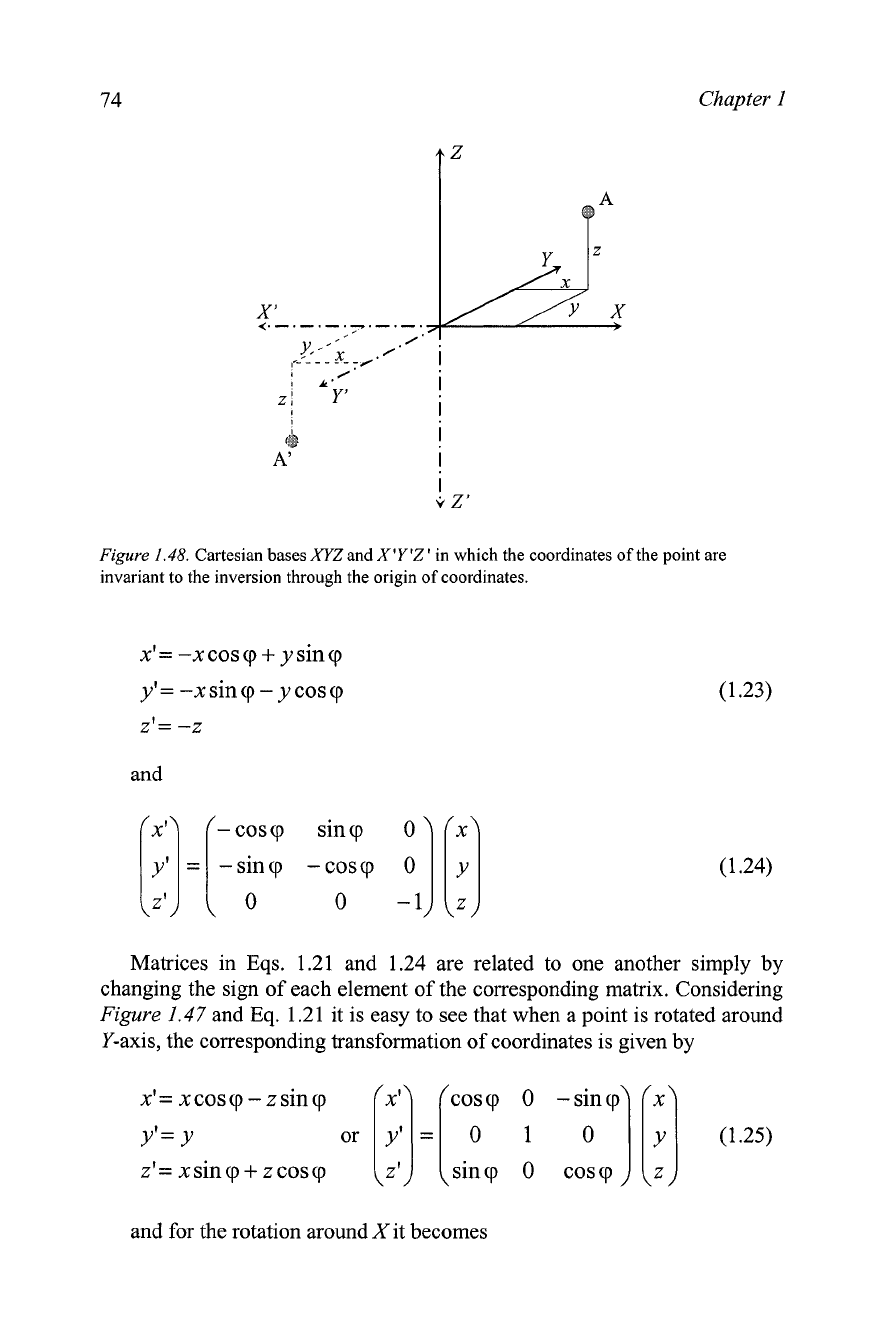
When two points in the same Cartesian basis are related to one another

via

inversion through the origin of coordinates, then the coordinates of the

inverted point are invariant with respect to a second Cartesian basis where

the directions of all axes are reversed as shown in

Figure

1.48.

Hence, the inversion through the origin of coordinates may be

represented algebraically as

When the two points are related to one another by roto-inversion, the

resulting linear transformation is a combination of Eqs. 1.20 and 1.21 with

Eq. 1.22:

Chapter

Figure

1.48.

Cartesian bases

Wand

X'Y'

Z '

in which the coordinates

invariant to the inversion through the origin of coordinates.

x'= -xcoscp+ ysincp

y'=

-xsincp- ycoscp

z'=

-2

and

the point are

Matrices in Eqs. 1.21 and 1.24 are related to one another simply by

changing the sign of each element of the corresponding matrix. Considering

Figure

1.47

and Eq. 1.21 it is easy to see that when a point is rotated around

Y-axis, the corresponding transformation of coordinates is given by

xl= xcoscp-zsincp

Y'=

[i]=pcp

-s:cp][:]

(1.25)

z'=

xsincp

zcoscp sin9

coscp

and for the rotation around

it becomes

Fundamentals of crystalline state

x'=

y'=ycosy-zsiny or y'

cosy -sin9

zl= ysin<p+zcosy

si:

cosy

A noteworthy property of matrices found in Eqs. 1.21, 1.22 and 1.24 to

1.26 is their unimodularity

the determinant of every matrix is equal to

-1 for the rotation and inversion (or roto-inversion) operations, respectively,

which is shown for the rotation around

in Eq. 1.27.

Because of the restrictions imposed on the values of the rotation angles

(see

Table

1.4), sincp and coscp in Cartesian basis are

1 or

-1

for one, two

and four-fold rotations, and they are ill2 or +&/2 for three and six-fold

rotations. However, when the same rotational transformations are considered

in the appropriate crystallographic coordinate system,' all matrix elements

become equal to

-1 or 1. This simplicity (and undeniably, beauty) of the

matrix representation of symmetry operations is the result of restrictions

imposed by the three-dimensional periodicity of crystal lattice. The presence

of rotational symmetry of any other order

(e.g. five-fold rotation) will result

in the non-integer values of the elements of corresponding matrices in three

dimensions.

When two points in the same Cartesian basis are related to one another

by a translation, then the coordinates of the second point are invariant with

respect to a different Cartesian basis, in which the orientations of the axes

remain the same as in the first basis but its origin is shifted along the three

non-coplanar vectors, t,,

and t,, as shown in

Figure

1.49.

Thus, considering

Figure

1.49 the coordinates,

x',

y',

z',

of the point A' in

the original basis

XYZ

are given as

The angles between

X-,

Y-,

and Z-axes are identical to

and

in the corresponding

crystal system (see

Table

11).

Chapter

Figure

1.49.

Cartesian bases

XYZ

and

X'Y

in which the coordinates of the point are

invariant to translations along three non-coplanar vectors

t,,

and

t,.

or in matrix notation

where t,, t, and

are the lengths of vectors tp t, and t,, respectively.

To generalize the results obtained in this section we now consider two

points, A and A', with coordinates x, y, z and x', y', z', respectively, in the

same Cartesian basis

XYZ.

unrestricted transformation of A into A' can

be carried out first, by applying the corresponding rotation (andlor inversion)

and second, by applying the corresponding translational transformation of

the coordinates. For example, assuming that rotation occurs around the

Z-

axis, and considering Eqs. 1.20, 1.21, 1.28 and 1.29, the relationships

between x, y,

and x',

y',

z' are given as follows

Fundamentals

crystalline state

or in matrix notation

1.20.2

Rotational transformations of vectors

Any change in the orientation of a vector representing a point without

changing the length and the position of the origin of the vector (see

Figure

1.50)

can be described as a new vector, which is a product of a specific

square matrix and the original vector. As we established in the previous

section (see Eqs. 1.21, 1.22 and 1.24 to 1.26), in three dimensions the matrix

has three rows and three columns, the vector has three rows, and the

resulting product is shown in general form in Eq. 1.32.

'-12 '-13 '-11'

'-12Y

'-13'

r21x+r22Y+r23z

'-3,'

'-32Y

'-33'

Using the following notations

equation 1.32 becomes

X'=

The matrix

is called rotation matrix since

(1.34)

the changing of the

orientation of the vector without altering its length and without moving its

origin away from the origin of the coordinate system is achieved by various

rotations of the vector,

e.g. around a point, around an axis, or by reflecting it

in a plane.

Chapter

Figure

1.50.

The point with the coordinates x,

z represented by the vector (x,

z) and the

second (symmetrically equivalent) point with the coordinates x',

y',

z' represented by the

vector (x',

y',

z'), which has the same length as the original vector (x,

z).

1.20.3

Translational transformations of vectors

When only the change of the length of the vector is involved, it is usually

much more convenient to move the origin of the coordinate system in a way

that the length and the orientation of the new vector remain the same in the

new basis as those of the original vector in the original basis (see

Figure

1.49).

This is achieved by translating the old origin of the coordinate system

by (t,, t,, and t3) along

and

respectively, which is equivalent to adding

two vectors as shown in Eq. 1.35.

Introducing the following notation in addition to

Eq.

1.33

the short form of

Eq.

1.35 becomes

X'= X+T

Fundamentals

crystalline state

1.20.4

Combined symmetrical transformations of vectors

Unrestricted transformations of a vector can, therefore, be represented

using a sequence of matrix-vector transformations by first, evaluating the

product of the rotation matrix and the original vector as shown in Eq. 1.32

and second, evaluating the sum of the obtained vector and the corresponding

translation vector, as shown in Eq. 1.35. The combined unrestricted

transformation is, therefore, represented in the expanded form using Eq.

1.38, or using the compact form as shown in Eq. 1.39.

It is practically obvious that simultaneously or separately acting rotations

(either proper or improper) and translations, which portray all finite and

infinite symmetry elements,

i.e. rotation, roto-inversion and screw axes,

glide planes or simple translations can be described using the combined

transformations of vectors as defined by Eqs.

1.38

and

1.39.

When finite

symmetry elements intersect with the origin of coordinates the respective

translational part in Eqs. 1.38 and 1.39 is 0, 0, 0; and when the symmetry

operation is a simple translation, the corresponding rotational part becomes

unity,

where

At this point, the validity of Eqs. 1.38 and 1.39 has been established

when rotations were performed around an axis intersecting the origin of

coordinates. We now establish their validity in the general case by

considering vector

and a symmetry operation that includes both the

rotational part,

and translational part,

Assume that the symmetry

operation is applied in a crystallographic basis where the rotation axis is

shifted

fiom the origin of coordinates by a vector

At.