Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Chapter

a result, we need to introduce the so-called infinite or translational symmetry

elements in addition to the familiar finite or non-translational symmetry

elements, which can be present in a lattice as well. Translation or shift is a

simple infinite symmetry element (see

Figure

1.7). When acting

simultaneously, translation and rotation result in screw axes; translation and

reflection in a mirror plane produce glide planes

(Table

1.3). Screw axes and

glide planes are, therefore, complex infinite symmetry elements.

1.13.1

Glide planes

The combination of a mirror reflection plane with the corresponding

translations that are always parallel to the plane, results in a total of five

possible crystallographic glide planes.' The allowed translations are 112 or

114 of the length of the basis vector, parallel to which the shift (i.e. gliding)

occurs. All possible glide planes are listed in

Table

1.15 together with their

graphical symbols. Since each of the glide planes produces an infinite

number of symmetrically equivalent objects from the original, the order of

the plane indicates the number of symmetrically equivalent objects within

the boundaries of one unit cell, and is also listed in

Table

1.15.

Table

1.15.

Crystallographic glide planes

Plane symbol Order Graphical symbola Translation vector

d14~

Shown in the following coordinate system:

is the diagonal vector, e.g.

c, etc., which depends on the

orientation of the plane with respect to crystallographic basis vectors.

Thus, there are three types of glide planes:

Glide planes a, b and c, which after reflecting in the plane translate an

object by 112 of the length of a,

and

basis vectors, respectively.

A sixth glide plane, e, has been introduced by de Wolff

al.

(see the footnote on page

10)

to resolve ambiguities occurring in some space groups (see section 1.16). For example,

space group Cmca, where the translation after the reflection in the a-plane occurs along

and

is identical to Cmcb, but the group becomes unique, i.e. Cmce, using the e plane.

Fundamentals

crystalline state

Because of this, for example, glide plane, a, can be perpendicular to

either b or

but it cannot be perpendicular to

Similarly, glide plane, b,

cannot be perpendicular to b, and glide plane, c, cannot be perpendicular

Since the translation is always by 112 of the corresponding basis

vector, these planes produce two symmetrically equivalent objects within

one full length of the corresponding basis vector (and within one unit

cell), i.e. their order is 2.

Glide plane n, which after reflecting in the plane translates an object by

112 of the length of the diagonal between the two basis vectors located in

the plane parallel to n. For example, glide plane, n, perpendicular to

will translate an object by 1/2(a

b). Glide plane n, results in two

symmetrically equivalent objects within the full length of the diagonal

vector (and within one unit cell) and its order is 2.

Glide planes d, which after reflecting in the plane translate an object by

114 of the length of the diagonal between the two basis vectors located in

the plane parallel to d. These planes, also known as "diamond" planes

since they are found in the diamond crystal structure, are always present

in pairs parallel to one another, and translate along different diagonals.

The length of the translation is 114, which results in a total of four

symmetrically equivalent objects per unit cell.

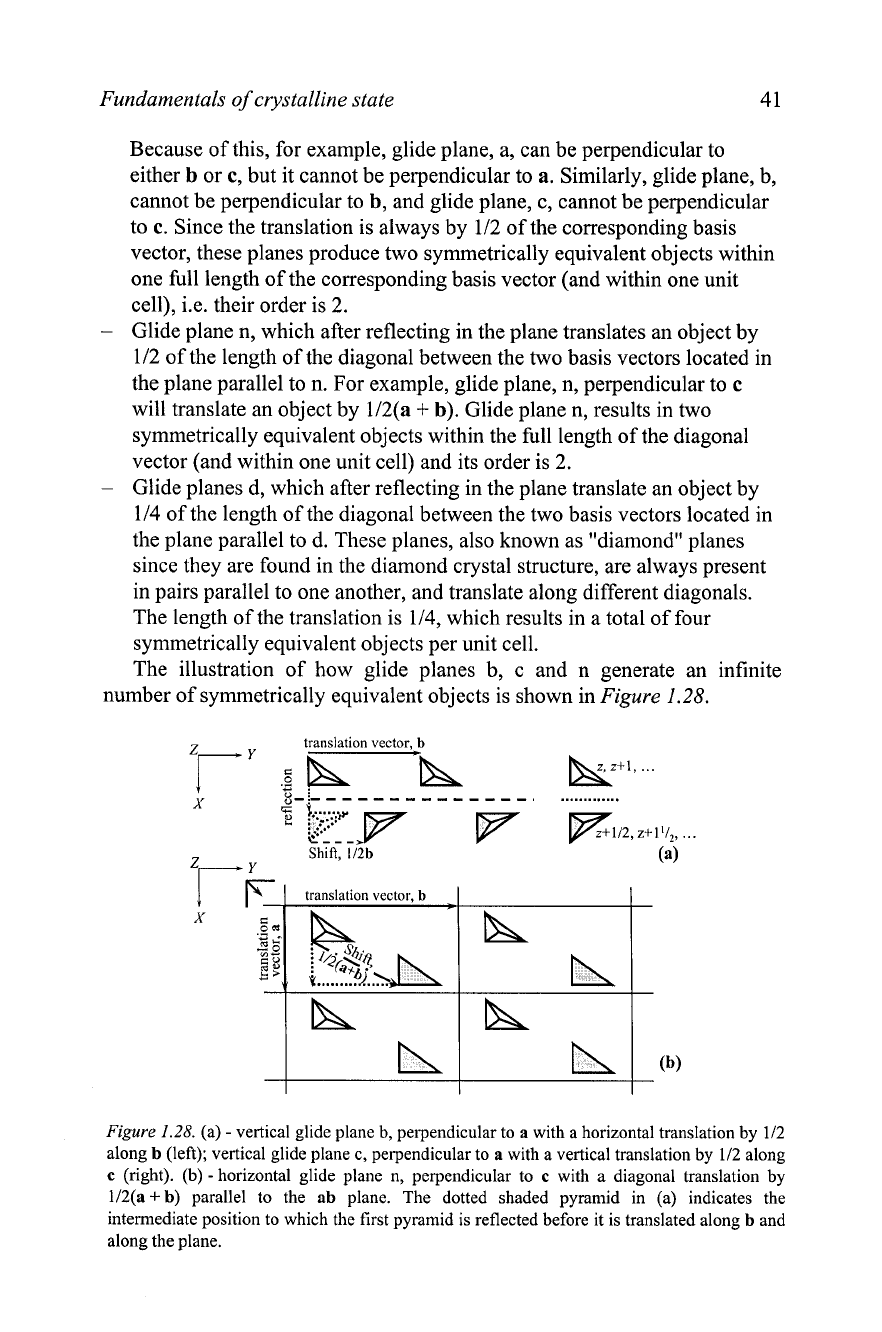
The illustration of how glide planes b, c and n generate an infinite

number of symmetrically equivalent objects is shown in

Figure

1.28.

.............

z+1/2, z+l1I2,

...

Shift,

112b

(a)

translation

vector,

Figure

1.28.

(a)

vertical glide plane b, perpendicular to a with a horizontal translation by 112

along

(left); vertical glide plane c, perpendicular to

with a vertical translation by 112 along

(right). (b) -horizontal glide plane n, perpendicular to

with a diagonal translation by

112(a

b) parallel to the ab plane. The dotted shaded pyramid in (a) indicates the

intermediate position to which the first pyramid is reflected before it is translated along b and

along the plane.

Chapter

1.13.2

Screw

axes

Screw axes perform a rotation simultaneously with a translation along the

rotation axis. In other words, the rotation occurs around the axis, while the

translation occurs parallel to the axis. Crystallographic screw axes include

only two-, three-, four- and six-fold rotations due to the three-dimensional

periodicity of the crystal lattice, which prohibits five-, seven- and higher-

order rotations. Hence, the allowed rotation angles are the same as for both

rotation and inversion axes (see

Eq.

1.2).

Translations, t, along the axis are also limited to a few fixed values,

which depend on the order of the axis, and are defined as t

k/N,

where

axis order, and k is an integer number between one and N-1. For instance,

for the three-fold screw axis, k

1 and 2, and the two possible translations

are 113 and 213 of the length of the basis vector parallel to this axis, whereas

for the two-fold axis, k

1, and only 112 translation is allowed.

The symbol of the screw axis is constructed as

to identify both the

order of the axis

(N)

and the length of the translation (k). Thus, the two

three-fold screw axes have symbols 31 and

whereas the only possible

two-fold screw axis is 2,. The International symbols, both text and graphical,

and the allowed translations for all crystallographic screw axes are found in

Table

1.16.

Table

1.16.

Crystallographic screw axes.

Axis order Text symbola Graphical symbola Shift along the axisb

2 21

1 12

6 61,6*.63,6,, 65

116,216,316,416, 516

Pairs of screw axes, in which the sums of the subscripts equal to the order of the axis are

called enantiomorphous pairs since one is the mirror image of another. The latter is

reflected in the graphical symbols of the corresponding pairs of the enantiomorphous axes.

These are:

and

32; 41

and

43;

and

65; 62

and

Two enantiomorphous axes differ only

by the direction of rotation or (which is the same) by the direction of translation.

Given as a fraction of a full translation in a positive direction assuming counterclockwise

rotation along the same axis.

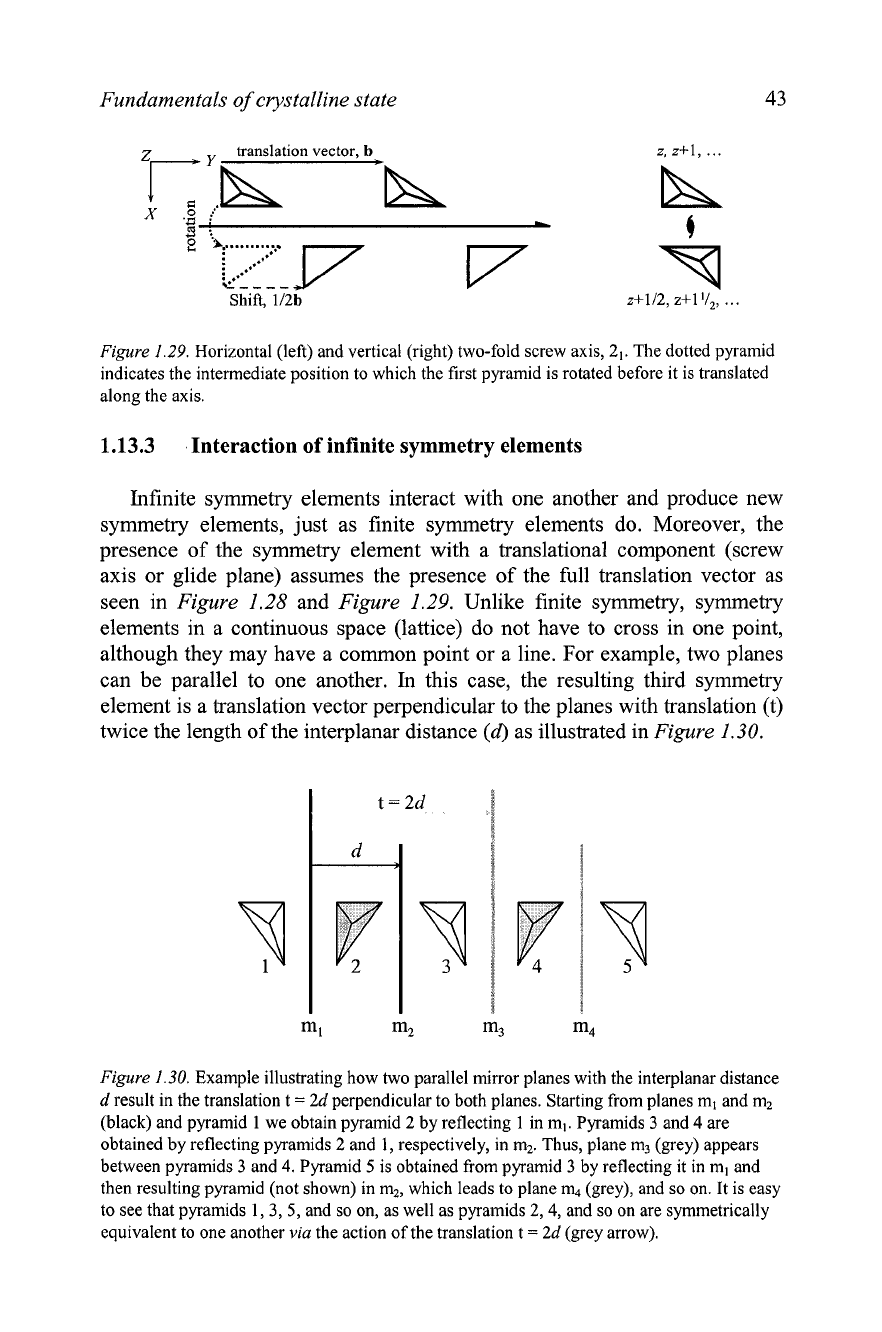
Figure 1.29

illustrates how the two-fold screw axis generates an infinite

number of symmetrically equivalent objects

via

rotations by 180" around the

axis with the simultaneous translations along the axis by 112 of the length of

the basis vector to which the axis is parallel.

Fundamentals

crystalline state

:.K

vector, b

zfl,

...

.........::..

...'

...*

c----

Shift,

1/2b

z+1/2,

z+11t2,

...

Figure

1.29.

Horizontal (left) and vertical (right) two-fold screw axis,

2,.

The dotted pyramid

indicates the intermediate position to which the first pyramid is rotated before it is translated

along the axis.

1.13.3

,Interaction of infinite symmetry elements

Infinite symmetry elements interact with one another and produce new

symmetry elements, just as finite symmetry elements do. Moreover, the

presence of the symmetry element with a translational component (screw

axis or glide plane) assumes the presence of the full translation vector as

seen in

Figure

1.28

and

Figure

1.29.

Unlike finite symmetry, symmetry

elements in a continuous space (lattice) do not have to cross in one point,

although they may have a common point or a line. For example, two planes

can be parallel to one another. In this case, the resulting third symmetry

element is a translation vector perpendicular to the planes with translation (t)

twice the length of the interplanar distance

(d)

as illustrated in

Figure

1.30.

Figure

1.30.

Example illustrating how two parallel mirror planes with the interplanar distance

result in the translation t

perpendicular to both planes. Starting from planes m, and m2

(black) and pyramid 1 we obtain pyramid

by reflecting

in ml. Pyramids 3 and

are

obtained by reflecting pyramids

and

respectively, in m2. Thus, plane m3 (grey) appears

between pyramids

and

Pyramid

is obtained from pyramid

by reflecting it in ml and

then resulting pyramid (not shown) in m2, which leads to plane m4 (grey), and so on. It is easy

to see that pyramids

1,3,5, and so on, as well as pyramids

2,4,

and so on are symmetrically

equivalent to one another

via

the action of the translation t

(grey arrow).

Chapter

Figure

1.31.

Example illustrating the result of interaction between the glide plane, b, and the

center of inversion,

The original symmetry elements are black and the derivatives are grey.

Another example (Figure

1.31)

illustrates the result of the interaction

between glide plane, b, and center of inversion. We begin from the

symmetry elements shown in black and marked in Figure

1.31

as b and

and pyramid A. Note, that the two symmetry elements do not share a

common point. Pyramid A is converted by the glide plane into

B; B

into

A',

and so on. The center of inversion converts

into

and so on. All objects

depicted in Figure

1.31

can be obtained using the two original symmetry

elements (keep in mind that although only

pyramids are shown in this

figure, their number is in reality infinite). The derived symmetry element

that converts

into

is the

screw axis. Additional derived symmetry

elements are translation

that transforms A into A', translation

other glide

planes, screw axes, and centers of inversion, as marked in Figure

1.31.

Thus,

the infinite structure is produced and its unit cell is shaded in the figure. It is

easy to see that in this infinite structure there are an infinite number of

symmetry elements, even though we started with just two of them: the glide

plane, b, and the center of inversion.

Note that only those symmetry elements which intersect the asymmetric

part of the unit cell are independent, exactly in the same way as only those

atoms that are found in the asymmetric part of the unit cell are independent

(see Figure

I.@.'

Once the locations of independent atoms and symmetry

elements in the unit cell are known, the whole crystal can be easily

Strict definition can be given as follows: two objects (atoms, molecules or symmetry

elements) are symmetrically independent if there is no symmetry operation that converts

one into another.

Fundamentals

crystalline state

Figure

1.32.

Characteristic distribution of the two-, three-, four-, and six-fold rotation axes

parallel to the unique axis in the unit cell in tetragonal (left), trigonal (center), and hexagonal

(right) crystal systems as the result of their interaction with lattice translations.

reconstructed. Symmetry elements interact with basis translations, which are

symmetry elements themselves. Hence, the three non-coplanar vectors that

form a three-dimensional lattice interact with symmetry elements and

distribute them together with their "sub-elements"

(e.g. a six-fold axis

contains both two- and three-fold axes as its sub-elements) in the specific

order in the unit cell and in the entire lattice.

The distribution of the inversion centers, two-fold axes and planes in the

unit cell can be seen in the previous

Figure

1.31:

these symmetry elements

are repeated along basis translation vectors every 112 of the full translation.

This is true for triclinic, monoclinic, and orthorhombic crystal systems, i.e.

crystal systems with low symmetry. Similar arrangements of symmetry

elements in tetragonal, trigonal, and hexagonal crystal systems are shown for

a primitive lattice in

Figure

1.32,

where only rotation axes perpendicular to

the plane of the projection were taken into account. The distribution of other

symmetry elements, including the infinite ones in primitive or centered

lattices follows the same path, but types of axes and their order may be

different.

The orientation and placement of crystallographic axes in a cubic crystal

system is more complex and it is difficult to illustrate in a simple drawing.

However, projections of rotation axes in cubic symmetry along the unit cell

edges resemble tetragonal symmetry, while projections along the body

diagonals of the cube resemble trigonal symmetry. The positions of

symmetry elements (especially finite) in the unit cell are important since

they are directly related to special site positions, which are discussed later in

sections 1.17 and 1.18.

1.14

Crystallographic planes, directions and indices

The crystallographic plane is a geometrical concept (mathematical

abstraction) introduced to illustrate the phenomenon of diffraction from ideal

crystal lattices since algebraic equations that govern diffraction process are

difficult to visualize. It is important to realize and remember that no "real"

Chapter

crystallographic planes exist in real crystals. Furthermore, regardless of

whether the crystallographic plane is referred to in singular or in plural, the

reference is always made to a series, which consists of an infinite number of

planes.

1.14.1

Indices

planes

Crystallographic planes are defined as a set (or family) of planes that

intersect all lattice points. All planes in the same family are: (1) parallel to

each other, and (2) equally spaced. The distance between neighboring planes

is called the interplanar distance or d-spacing. The family of crystallographic

planes is described using three integer indices h, k, and I, which are called

crystallographic or Miller indices.' When referring to a plane, a triplet of

Miller indices is always enclosed in parentheses: (hkl). Miller indices

indicate that the planes that belong to the family (hkl) divide lattice vectors

(unit cell edges) a,

and c into h, k and

equal parts, respectively. When the

planes are parallel to the crystallographic axis, the corresponding Miller

index is set to

The meaning of the Miller indices can be better understood after

considering Figure

1.33

through Figure

1.37.

Figure

1.33

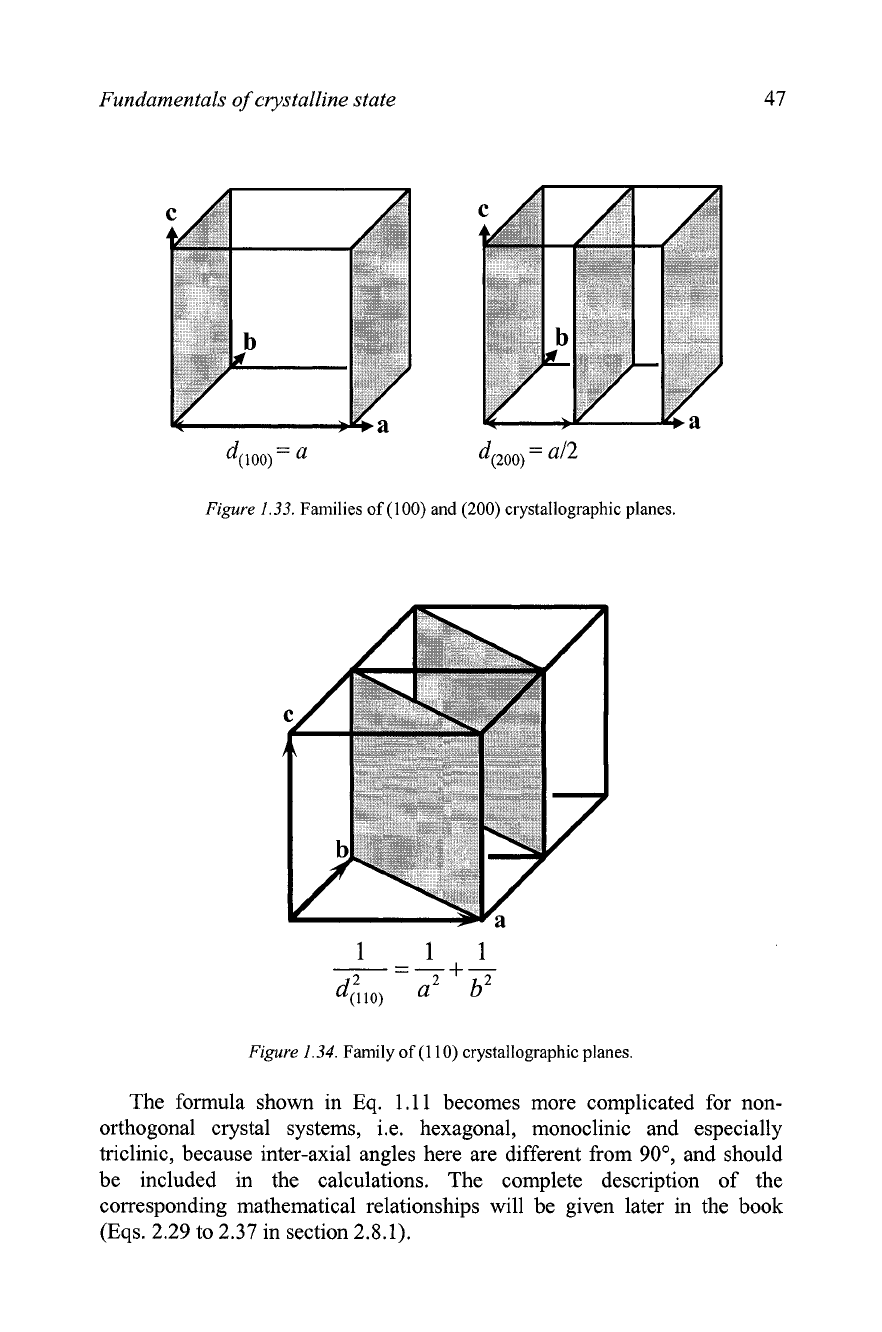
both sets of

planes are parallel to

and c. Hence, in both cases k

0. The set of

planes shown on the left divides a into one part, while the planes shown on

the right, divide a into two equal parts. This results in the following Miller

indices: (100) for the drawing on the left, and (200) for that on the right of

Figure

1.33.

It is obvious that the interplanar distance d(zoo, is 112 that of

d(loo,, and the (200) family of crystallographic planes is considered as the

second order of the (100) family. Following the same rules, the planes

shown in Figure

1.34

are parallel to c and divide both a and

in one part,

which results in the (1 10) Miller indices for this family of crystallographic

planes. Similarly, Figure

1.35

illustrates the (iil) and Figure

1.36

illustrates the (2 13) crystallographic planes.

Assuming that

90•‹, the interplanar distances for these

examples of crystallographic planes are shown at the bottom of each figure.

A general formula

(Eq.

1.11) for the three orthogonal crystal systems (cubic,

tetragonal and orthorhombic) illustrates dependence of the d-spacing on the

Miller indices of the family and the lengths of the three unit cell edges.

In the hexagonal crystal system, a total of four Miller indices are sometimes used to

designate a plane:

(hkil),

where

-(h

k).

See

Figure

1.37

for details.

Fundamentals

crystalline state

Figure

1.33.

Families of (100) and (200) crystallographic planes.

Figure

1.34.

Family of

10)

crystallographic planes.

The formula shown in

Eq.

1.11 becomes more complicated for non-

orthogonal crystal systems, i.e. hexagonal, monoclinic and especially

triclinic, because inter-axial angles here are different from

90•‹, and should

be included in the calculations. The complete description of the

corresponding mathematical relationships will be given later in the book

(Eqs.

2.29 to 2.37 in section 2.8.1).

Chapter

Figure

1.35.

Family of

(771)

crystallographic planes.

Figure

1.36.

Family of

(213)

crystallographic planes.

hexagonal and trigonal crystal systems, the fourth index is usually

introduced to address the possibility of three similar choices in selecting the

crystallographic basis as illustrated in

Figure

1.37.

addition to the unit cell

based on the vectors a, b and c, two other unit cells, based on the vectors a,

-(a

b) and

and -(a

b),

and c are possible due to the six-fold or the

Fundamentals

crystalline state

Figure

1.37.

Three possibilities to select the crystallographic basis in hexagonal and trigonal

crystal systems and the family of

120)

crystallographic planes in the hexagonal crystal

system. Indices are shown in the unit cell based on the vectors

and

Three additional

symmetrically related families of planes have indices

(ii20), (7210)

and

(2770)

in the same

basis and we leave their identification to the reader.

three-fold rotational symmetry parallel to c, respectively. Thus, if only three

indices are employed to designate symmetrically related planes (e.g. the

darkest-, the lightest- and the medium-shaded planes in Figure 1.37), these

are (1

lo), (120) and (210) planes, respectively, defined in the lattice based

on the unit vectors

and c. No apparent relationships are seen between

the three planes designated using three indices. When the fourth index, i

-(h

k), is introduced, the three planes (hkil) are only different by a cyclic

permutation of the first three indices, thus emphasizing symmetrical

relationships existing between these families of crystallographic planes.

1.14.2

Lattice directions and indices

Directions in the crystal lattice are described using lines that pass through

the origin of the lattice and are parallel to the direction of interest. Since the

lattice is infinite, a line drawn in any direction from its origin will

necessarily pass through the infinite number of lattice points. For example,

the line traversing the origin and parallel to the body diagonal of the unit

---

cell, passes through the points nnn,

. .

2 2 2, 1 1 1, 000, 1 1 1,222,

nnn.

The crystallographic direction is therefore, indicated by referring to the

coordinates (u, v and w, see Eq. 1 .l) of the first point other than the origin,

which the line intersects on its way from the origin. To differentiate between

indices of the crystallographic planes,

indices of the crystallographic

directions are enclosed in square brackets [uvw], as shown in Figure 1.38.