Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Chapter

contains crystallographic data about more than 64,000 inorganic compounds.

The frequency of the occurrence of various space groups is far fiom uniform

and it varies for different classes of materials.

Organic compounds mostly crystallize in the low symmetry crystal

systems: 95% of the known organic crystal structures have orthorhombic or

lower symmetry. In particular, -76% of known organic crystal structures

belong to only 5 space groups symmetry:

P2Jc (29.2%), P212121 (19.8%),

(1 1.1%), P2, (10.9%), and C21c (5.4%). Furthermore, only 12 space

groups account for 87% of the organic compounds.' On the contrary, the

majority of inorganic compounds crystallize in space groups with

orthorhombic or higher symmetry. In order of decreasing frequency, they are

as follows:

Fm?m, Pnma, Fd?m, P2,/c, P63/mmc, ~m?m, ~?m, C2lm and

C21c. A total of 12 crystallographic space groups account for approximately

50% of structures of inorganic compounds.

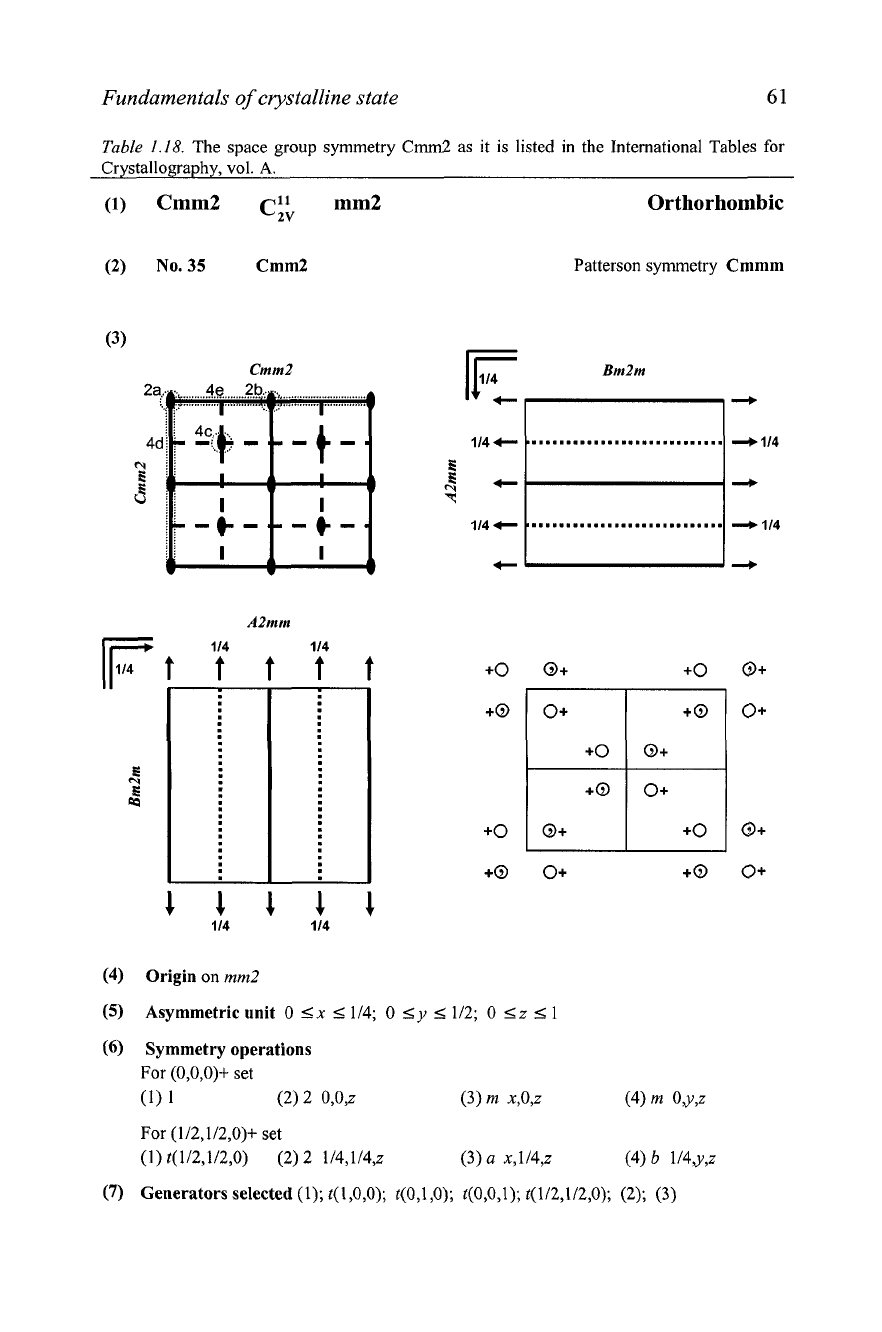
1.17

International Tables for Crystallography

example of how each of the 230 three-dimensional crystallographic

space groups is listed in the International Tables for Crystallography2 is

shown in

Table

1.18.

Explanations of what information is found in different

fields (the fields are numbered in the first column) follows.

There are 12 fields in

Table

1.18;

each of them contains the following

information:

Headline. Provides the short international (Hermann-Mauguin) space

group symmetry symbol (Cmm2) followed by the Schonflies symbol of

the same space group

(c&

these symbols are not discussed in this

book), the corresponding point group symmetry symbol (mm2) and the

name of the crystal system (Orthorhombic).

2. Second headline. Includes the sequential number of the space group

symmetry

(35)

followed by the full international (Hermann-Mauguin)

symbol (Cmm2, since in this case the full symbol is the same as the short

one) and Patterson symmetry (Cmmm). Although the Patterson function

will be discussed in Chapter 2, it is worth noting that the Patterson

symmetry is derived

fiom the symmetry of the space group by replacing

all screw axes and glide planes with the corresponding finite symmetry

elements, and by adding a center of inversion, if it is not present in the

space group.

Donohue, Revised space-group frequencies for organic compounds, Acta Cryst.

A41,

203

(1985).

Format varies in earlier editions of the International Tables for Crystallography; here we

follow the format adopted in volume

since the

1983

edition.

Fundamentals

crystalline state

Table

1.18.

The

space group symmetry Cmm2 as it is listed in the International Tables

for

Crystallography, vol.

(1)

Cmm2

c;;

mm2 Orthorhombic

(2)

No.

Cmm2

Patterson symmetry

Cmmm

Origin

mm2

Asymmetric unit

0 <x

114; 0

1/2; 0

Symmetry operations

For

(0,0,0)+

set

(1)

(2) 2 o,o,z (3)

x,O,z (4)

O,Y,~

For

(112,1/2,0)+

set

(1)t(1121120) (2)2 114,114,~ (3)

114,z (4) b 114,~~~

Generators selected

(1);

t(1,0,0); t(0,1,0); t(0,0,1); t(1/2,1/2,0); (2); (3)

Chapter

(8)

Positions

Coordinates Reflection conditions

Multiplicity,

Wyckoff letter,

Site symmetry (O,O,O)+ (1/2,112,0)+ General:

1 (1) x,Y, z (2)

z (3)

z hkl: h+k=2n

(4)

Y, z

Okl: k=2n

h01: h=2n

hkO: h+k=2n

hOO: h=2n

OkO: k=2n

Special: as above, plus

m.. 0, y, z 0,

z no extra conditions

no extra conditions

hkl

h=2n

no extra conditions

2 amm2 0,0,z no extra conditions

(9)

Symmetry of special projections

Along [OOl] c2mm Along [loo] plml Along [OlO] p11m

a'=a b '=b

at=1/2b b'=c a'=cbt=1/2a

Origin at 0,0,z Origin at x,O,O Origin at O,y,O

Maximal non-isomorphic subgroups

[2] C 1

2(P2)

;2)+

[~ICI ml(~m) (1;3)+

[2]Cml1 (Cm)

;4)+

IIa

(11)

IIc

Maximal isomorphic subgroups of lowest index

[3]Crnm2

(af=3a

or b1=3b); [2]Cmm2 (c1=2c)

Minimal non-isomorphic supergroups

[2]Cmmm; [2]Cmma; [2]P4mm; [2]P4bm; [2]P4~cm;

[2]P4,nm; [2]~4 2m; [2]~a 21m; [31Mmm

Fundamentals

crystalline state

Swace mouw symmetry diagrams are shown as one or several (up to

orthogonal projections along different unit cell axes. The projection

direction is perpendicular to the plane of the figure. Projection directions,

orientations of axes and selection of the origin of the coordinates are

dependent on the crystal system, and a full description can be found in

the International Tables for Crystallography, vol.

The schematic for

the orthorhombic crystal system is shown in

Figure

1.42.

If the

horizontal symmetry element is elevated above the plane of the

projection by a fraction of the translation along the projection direction

other than

or 112, its elevation is shown as the corresponding fraction,

i.e., 118, 114, and so on.

additional diagram shows symmetrically

equivalent points (both inside and in the immediate vicinity of one unit

cell) that are related to one another by the symmetry elements present in

the orientation matching the first diagram.

4. Origin of the unit cell. It is given as the site symmetry and its location, if

necessary. In the example shown in

Table

1.18

the origin of the unit cell

is located on mm2, i.e. on the two-fold axis, which coincides with the

line where the two perpendicular mirror planes intersect.

this example,

the origin can be chosen arbitrarily on the Z-axis since there are no

symmetry elements with a fixed

z-coordinate in the space group Cmrn2.

Figure

1.42.

Schematic representation of orthorhombic space group symmetry diagrams

showing the origin of coordinates (O), the labels of the axes

(a,

and

and the projection

directions ([OOl], [OIO] and [I 001). The box marked "General" is a general position diagram

(see the description of fields No.

and

below). The triplets (abc and so on) indicate

settings symbols that result in the corresponding space group symbols. Each settings symbol

is obtained by a permutation of the unit cell axes, e.g. cab is the cyclic permutation of abc:

c, b'

a, c'

b. It should be noted that a space group symbol is invariant to the changes of

the sign (direction) of the axes.

64 Chapter

Asymmetric unit represents the fraction of the unit cell, which generally

contains symmetrically inequivalent points. It is delineated by the

elementary parallelepiped specified in terms of fractions of the

corresponding unit cell edges

(i.e. 0

114,O

112 and 0

and (if necessary) by including supplementary restrictions, e.g.

(l+y)/2; y

x12 as in the space group ~?ml.

Symmetry operations. For each point with coordinates

in the

general position, the symmetry operation which transforms this point into

symmetrical equivalent is listed together with its sequential number. The

term general position applies to any point in the unit cell that is not

located on any of the finite symmetry elements present in the group.

Symmetry operations in the non-primitive space groups are divided into

sets. The sets are arranged based on the translation vector(s)

corresponding to Bravais lattice centering, which are added to the

coordinates of each point in the unit cell. The first set is always the

(0,0,0)+ set, which represents the primitive basis that is enough to

describe the same but primitive space group symmetry (in this case it is

Pmm2). The second set in Table

1.18

is (1/2,1/2,0)+ set, which accounts

for the presence of the base-centered lattice,

Each symmetry operation

in addition to its sequential number (in parenthesis) lists the nature of the

operation (t stands for translations) and its location. For example,

t(1/2,1/2,0) stands for the translation of the point by 112 along both

(or

and

(or

Y);

the notation

(x,

114,

specifies glide plane, a,

perpendicular to

and intersecting

114.

Generators selected specify the minimum set of symmetry operations,

including translations that are needed to generate the space group

symmetry. They begin with translations (the first three represent full

translations along the three major crystallographic axes and the fourth is

the translation reflecting the presence of the base-centered Bravais lattice,

C) followed by the numbers of symmetry operations

fkom the first set in

the previous field. Hence, the space group

Crnrn2 can be generated by

using symmetry operations No. 2 (the two-fold axis coinciding with

and No.

(the mirror plane perpendicular to

and intersecting

at y

in addition to four translations.

Positions. This field contains standardized information about possible

locations (or sites) that can accommodate points (or atoms) in the unit

cell and corresponding reflection conditions. Reflection conditions show

the limitations on the possible combinations of Miller indices that are

imposed by the symmetry of the space group and these will be discussed

in Chapter 2, sections 2.12.3 and 2.12.4. Each record in this field

corresponds to one site and each site is listed starting with the

multiplicity of the site position (integer numbers,

8,4,4,

. .

2) followed

Fundamentals

crystalline state

by Wyckoff letter

(f,

. .

a),

site symmetry

(1,

m.., .m.,

mm2),

and coordinate triplets of the symmetrically equivalent atoms. The

multiplicity of the site position is the total number of symmetrically

equivalent atoms that will appear in one unit cell as the result of having

an atom with the coordinates corresponding to any of the listed triplets.

For example, the multiplicity of the second site (Wyckoff notation is e) is

The x-coordinate of any independent atom in this site is fixed at 0,

while y- and z-coordinates may vary between 0 and 1. Assume that y

0.15 and z

0.3 1. The complete list of four symmetrically equivalent

atoms in this position is obtained as follows. Atom1 (0, y,

plus (0, 0,

O):x=O,y=0.15,~=0.31;Atom2(0,

~,z)plus(O,O,O):x=O,y=

0.85,'z=0.31;Atom3 (O,y,z)plus(1/2, 112,0):x=0.5,y =0.65,z=

0.31; Atom4 (0, ~,z)plus(1/2, 112, 0):~=0.5,y=0.35,~=0.31. Site

positions in this field are arranged according to their multiplicities (from

the highest to the lowest) and according to site symmetry (from the

lowest to the highest). Wyckoff letters are assigned to site positions

starting with "a" for the site with the lowest multiplicity and the highest

symmetry. The coordinate triplets for the site with the highest

multiplicity and the lowest symmetry (general position) are listed with

the numbers of symmetry operations that generate this atom (as they

appear in field 6).

Symmetw of special proiections is usually given along

X-,

Y-

and Z-axes,

and in crystal systems with higher symmetry also along diagonals

together with the axes and the origin of the projected unit cell. These

projections correspond to two-dimensional crystallographic groups.

10-12. The closest

submoups and supermoups, their axes and other relevant

information. The discussion of these fields goes beyond the scope of this

book and the International Tables for Crystallography, vol. A should be

consulted for further details.

1.18

Equivalent positions

As briefly mentioned in the previous section, equivalent positions (or

sites) that are listed in the field No. 8 in

Table

1.18

for each crystallographic

space group, represent sets of symmetrically equivalent points found in one

unit cell. All equivalent points in one site are obtained from an initial point

by applying all symmetry operations that are present in the unit cell. The

fractional coordinates (coordinate triplet) of the initial (or independent) point

are usually marked as

Any negative coordinate (i.e.

-0.15)

may

converted into a positive coordinate by

adding a full translation along the same axis, i.e.

-0.15

0.85.

66 Chapter 1

1.18.1 General and special equivalent positions

The equivalent position is called general when the initial point is not

located on any of the finite symmetry elements (i.e. those that convert the

point into itself), if they are present in the group. The general equivalent

position has the highest multiplicity, and every one of the 230 space groups

has only one general site. However, since the only limitation on the possible

values of x, y and z in the coordinate triplet is imposed by geometrical

constraints that prevent neighboring atoms from overlapping with one

another, multiple sets of atoms occupying the general site with different

coordinate triplets of independent atoms are possible in many crystal

structures. An atom in the general equivalent position in any of the 230

three-dimensional space groups always has three positional degrees of

freedom, i.e. each of the three coordinates may be changed independently.

When a point (or an atom) is placed on a finite symmetry element that

converts the point into itself, the multiplicity of the site is reduced by an

integer factor when compared to the multiplicity of the general site. Since

different finite symmetry elements may be present in the same space group

symmetry, the total number of different "non-general" sites (they are called

special sites or special equivalent positions) may exceed one. Contrary to a

general equivalent position, one, two or all three coordinates will be

constrained in every atom occupying a special equivalent position.

Both the multiplicity and Wyckoff letter combined together, are often

used as the name of the equivalent position. Sometimes when

crystallographic data are published, the coordinates of all independent atoms

are given in reference to equivalent positions they occupy. For example if in

a hypothetical crystal structure nickel atoms occupy the site 4(c) in the space

group Cmm2, they can be listed as "Ni in 4(c), z = 0.1102", which indicates

that there are a total of four nickel atoms in the unit cell and one of them has

the coordinates x = 1/4, y = 1/4, z = 0.1102. The coordinates of the remaining

three nickel atoms are easily determined from the coordinates of all

symmetrically equivalent points in the position 4(c), see Table 1.18.

1.18.2 Special sites with points located on mirror planes

The first example of a special position was considered above (see page

65), when we analyzed the coordinates of four symmetrically equivalent

atoms located in the mirror plane in the space group Cmm2. Both this site

and the corresponding mirror plane are marked as 4e in the first diagram in

Table 1.18. A different special position on a different mirror plane in this

space group symmetry is marked as 4d in the same figure. Two additional

examples are found in Figure 1.43.

Fundamentals

crystalline state

Figure

1.43.

Constraints imposed on the coordinates of atoms located on diagonal mirror

planes (thick solid lines) in tetragonal (left) and hexagonal (right) crystal systems.

the tetragonal crystal system (Figure 1.43, left), diagonal mirror planes

perpendicular to the

plane are possible. When an atom is placed in the

special position on this plane, its coordinates are restricted in a way that

x and

may assume any value. This relationship is usually emphasized

by specifying the corresponding coordinate triplet as x, x, z. Similarly, in the

hexagonal crystal system (Figure 1.43, right) multiple diagonal mirror

planes perpendicular to the

XYplane are possible. When an atom is placed in

the special position on the mirror plane nearest to the Y-axis, its coordinates

are restricted such that

2x and

varies freely. The corresponding

coordinate triplet becomes x, 2x,

Considering the two remaining mirror

planes and moving clockwise, the point that belongs to the next mirror plane

will have coordinate triplet x, x,

(i.e. the same as in the case of the diagonal

mirror plane in the tetragonal crystal system), and for the third mirror plane

the triplet becomes x, 1/2x,

(or 2x,

2).

Therefore, any atom in a special position where it belongs to a mirror

plane has two positional degrees of fi-eedom. Only two of the three

coordinates vary independently, whereas the third is restricted to either a

constant value [e.g. position 4(e) in the space group Cmm2] or it is

constrained to be proportional to one of the two free coordinates (Figure

1.43). Similar to a general position, any special position on the mirror plane

can accommodate many independent atoms provided they do not overlap.

1.18.3

Special sites with points located on rotation or inversion axes

Both the rotation and inversion axes can also be the source of special

positions. Consider, for example, the site 2a (Table 1.18) where atoms are

accommodated by the two-fold rotation axis that follows the line at which

two mutually perpendicular mirror planes intersect. In this case two of the

three coordinates in the triplet are fixed (x

0 and

0), while the third

coordinate (z) may assume any value.

similar special position is

represented by the site 4c (Table 1.18), where the two-fold rotation axis is

parallel to

and coincides with the line at which two mutually perpendicular

Chapter

glide planes (a and b) intersect.

this position the two coordinates (x and

are fixed at x

114 and

varies. Note that the multiplicities of these two

sites (2a and 4c) are different, as they are defined by the total number of

symmetrically equivalent points in the given space group symmetry.

Two-fold axes can also be parallel to face

diagonal(s) in tetragonal,

hexagonal and cubic crystal systems, and one example for a cubic crystal

system is shown in Figure 1.44. The coordinates of a point (open circle)

located on the two fold axis that coincides with the diagonal of a square face

of the cube are constrained at x, x,

As we already know, there are four

three-fold rotation or inversion axes coinciding with the body diagonals of

the cube in the cubic crystal systems. Also shown in Figure 1.44 is one of

these three-fold rotation axes, where the coordinates of a point located in the

special position defined by the orientation of this crystallographic axis (filled

circle) will be constrained at x, x, x.

Therefore, the number of positional degrees of freedom is further reduced

to only one independent coordinate in special positions where atoms are

located on rotation or inversion crystallographic axes. Similar to both the

general position and special sites on mirror planes, any special equivalent

position on a rotation or inversion axis can accommodate many independent

atoms (geometrical constraints are always applicable).

1.18.4

Special sites with points located on centers of inversion

Atoms can also reside on centers of inversion. Since there is no inversion

center in the space group Cmm2, which was considered in Table 1.18, we

turn our attention to the distribution of the centers of inversion in the unit

cell that belongs to the triclinic space group symmetry

(Figure 1.45).

Figure

1.44.

Constraints imposed on the coordinates of atoms located on the diagonal two-

fold and three-fold rotation axes in cubic crystal system.

Fundamentals

crystalline state

Figure

1.45.

The distribution of the inversion centers in the triclinic space group symmetry

pi.

Eight independent centers are labeled from "a" through

"h".

Inversion centers that are

equivalent to one another are marked using symbols of the same size and shading. The

"invisible" centers are drawn using dotted lines.

There are eight independent centers of inversion per unit cell in this

group. They are labeled from "a" through

"h".

If an atom occupies the center

marked as "a" in

Figure

1.45,

it has the coordinates O,0,

This triplet is the

same as 0, 0, 0 since a point can always be shifted in any direction by a full

translation. If the center of inversion marked as

"h"

is occupied, the

coordinates of an atom in this special position are restricted to 112, 112, 112.

The list can be continued, and it is easy to see that regardless of which of the

available centers of inversion is occupied by an atom, all three coordinates of

this atom are determined by the location of the center.

Thus, there are no positional degrees of freedom available to an atom

occupying any special position created by the presence of the center of

inversion. Furthermore, unlike in the cases when atoms are located on the

mirror planes and rotation or inversion axes, only one atom can occupy any

single special position on the center of inversion.

1.19

Symbolic description of symmetry operations

So far we used both geometrical and verbal tools to describe symmetry

elements (e.g. plane, axis, center and translation) and operations (e.g.

reflection, rotation, inversion and shift). This is quite convenient when the

sole purpose of this description is to understand the concepts of symmetry.

However, it becomes difficult and time consuming when these tools are used

to work with symmetry, for example to generate all possible symmetry

operations, e.g. to complete a group. Therefore, two other methods are

usually employed: