Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Chapter

First, we select a new basis in which the rotation axis intersects with the

origin of coordinates. This is equivalent to changing the coordinates of the

original vector from

where

According to Eq. 1.39, the symmetry transformation in the new basis

results in vector

x',

where

After switching back to the original basis by applying negative

translation

-At

to the right hand part of Eq. 1.42 we obtain the coordinates of

the symmetrically equivalent vector

in the original basis as

where

is unity matrix. Noting that (R

E)At

i.e. it is the

translational part that reflects the shift of the rotation axis from the origin of

coordinates in addition to the conventional translational part, t, Eq. 1.43

becomes identical to Eq. 1.39. Thus, equations 1.38 and 1.39 are valid for

any crystallographic transformation in three dimensions.

It may be useful to briefly summarize the main properties of rotation

transformation matrices,

some of which were already mentioned above:

conventional crystallography matrix elements may accept only the

following values:

is unimodular:

The inverse rotation matrix is the same as the direct matrix, i.e.

R-'

when the rotation order is

or 2, otherwise

R-'

represents rotation in the

opposite direction.

order of an axis represented by the operation R can be determined in

two steps:

the case of an inversion axis, when det(R1)

-1,

the matrix should

be converted to a simple rotation by multiplying its elements by -1

Fundamentals

crystalline state

The order of the axis

(N)

is determined fkom the number of

multiplications of the matrix

by itself that are required to obtain the

unity matrix,

1.20.5

Augmented matrices

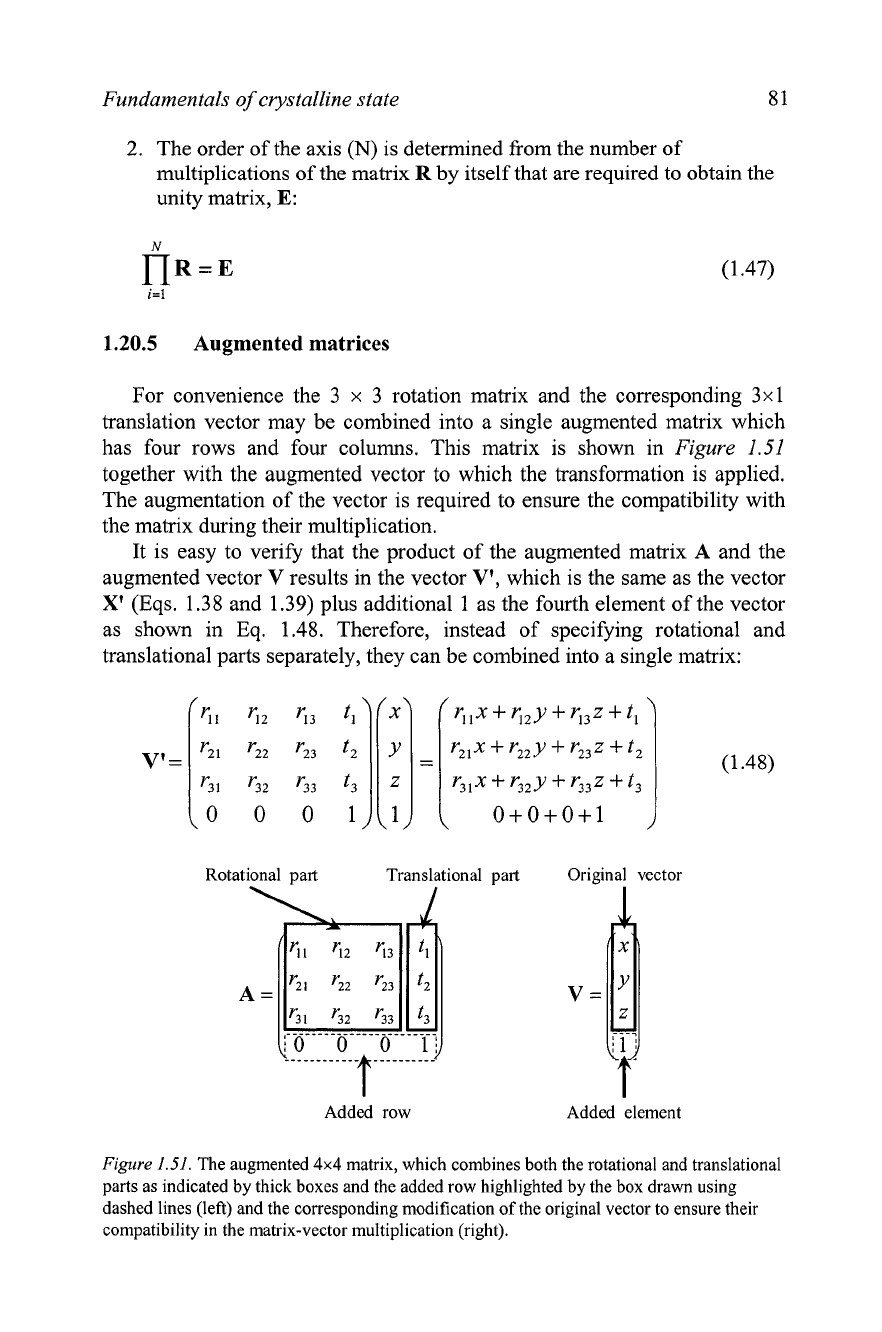
For convenience the

3 rotation matrix and the corresponding 3x1

translation vector may be combined into a single augmented matrix which

has four rows and four columns. This matrix is shown in

Figure

1.51

together with the augmented vector to which the transformation is applied.

The augmentation of the vector is required to ensure the compatibility with

the matrix during their multiplication.

It is easy to verify that the product of the augmented matrix

and the

augmented vector V results in the vector V1, which is the same as the vector

X1 (Eqs.

1.38

and 1.39) plus additional 1 as the fourth element of the vector

as shown in Eq.

1.48.

Therefore,

instead of specifying rotational and

translational parts separately, they can be combined into a single matrix:

Rotational

art

Translational uart

Original vector

Added row Added element

Figure

1.51.

The augmented

4x4

matrix, which combines both the rotational and translational

parts as indicated by thick boxes and the added row highlighted by the box drawn using

dashed lines (left) and the corresponding modification of the original vector to ensure their

compatibility in the matrix-vector multiplication (right).

Chapter

1.20.6

Algebraic representation of crystallographic symmetry

Considering conventional crystallographic symmetry, the elements

representing rotations, i.e.

rij,

are restricted to

or -1, and the elements

representing translations, i.e.

Eq.

1.48, are restricted to

112,

113, +1/4,

116,

118 including their integer multiples, and

In this way, all possible

transformations of atoms by symmetry operations are represented by the

multiplication of matrices and vectors.

Therefore, symmetrical transformations in the crystal are formalized as

algebraic (matrix-vector) operations

an extremely important feature used in

all crystallographic calculations in computer software. The partial list of

symmetry elements along with the corresponding augmented matrices that

are used to represent symmetry operations included in each symmetry

element is provided in

Table

1.19

and

Table

1.20.

For a complete list,

consult the International Tables for Crystallography, vol.

Table

1.19.

Selected symmetry elements, their orientation and corresponding symmetry

operations in the algebraic form as augmented matrices (see

Figure

1.51).

Symmetry Transformed First Second Third Fourth

element and coordinates symmetry symmetry symmetry symmetry

orientation operation operation operation operation

None None

0,0,0

None

-X,

-y,

-z

1000 -100112

%,%,%

y, z;

None

1/2-x,1/2-Y,l/z-z

0 0

0 0 0

-1

112

None

Fundamentals

crystalline state

Symmetry Transformed First Second Third Fourth

elementand coordinates symmetry symmetry symmetry symmetry

orientation operation operation operation operation

None

Chapter

Symmetry Transformed First Second Third Fourth

elementand coordinates symmetry symmetry symmetry symmetry

orientation operation operation operation operation

llX

x, Y, z;

through

0,0,0

x, -y, -z

x, Y, z;

through

0,0,0

-x, y, -z

x, Y, z;

through

0,0,0

-x, -y, z

llX

x, Y, z;

through

0,0,0

%+x, -y,

-Z

x, Y, z;

llZ

-Y,

x-Y, z;

through

0,0,0

y-x, -x,

x, Y, z;

-y,x-y,

/3+z;

through

0,0,0

y-x,-x,2/3+z

x, Y, z;

-Y, x, z;

through

0,0,0

-x, -y,

-4

x, Y, z;

-y, x, 1/4+z;

through

0,0,0

-x, -y, 1/2+z;

y, -x, 314+z

None

Fundamentals

crystalline state

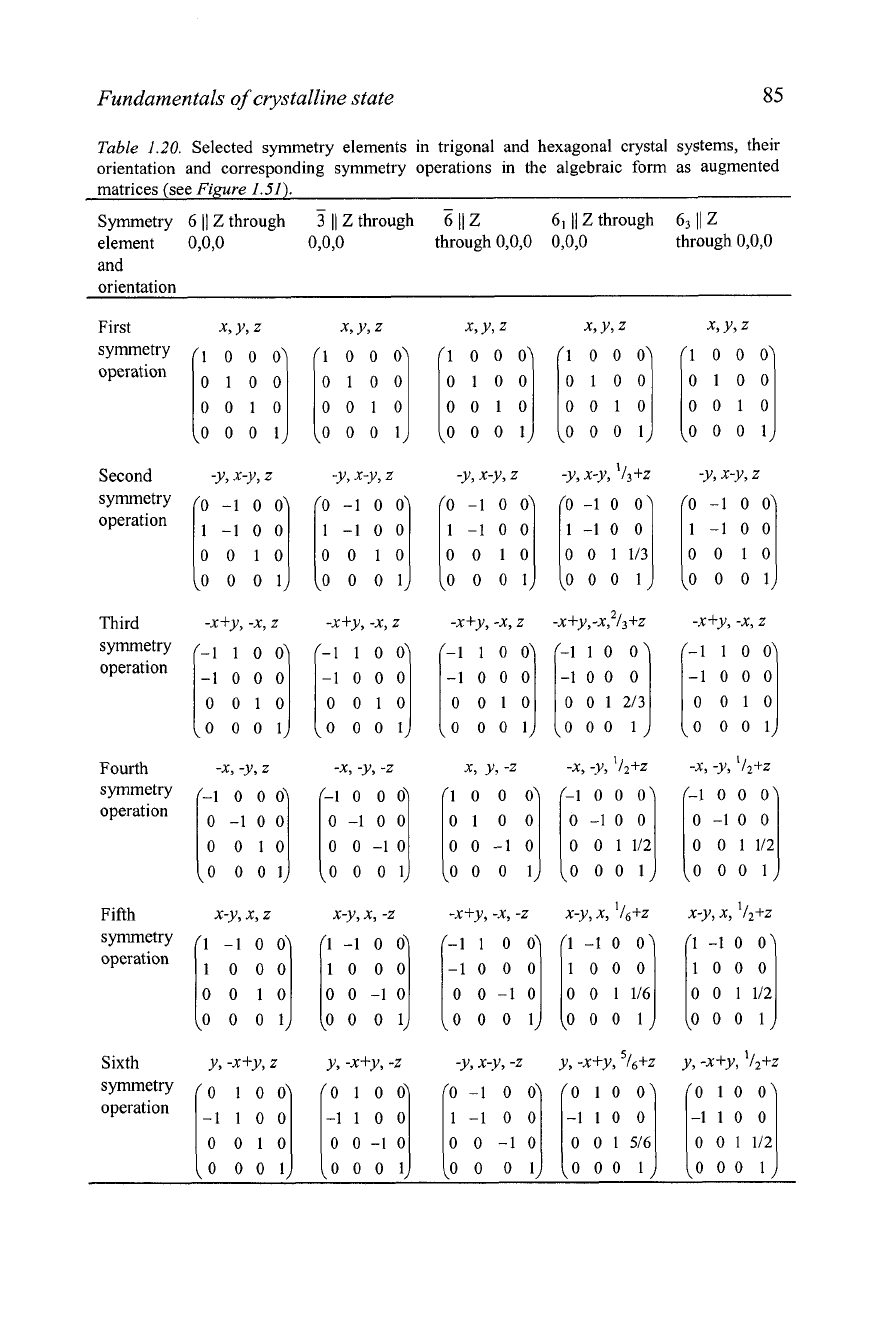
Table

1.20.

Selected symmetry elements in trigonal and hexagonal crystal systems, their

orientation and corresponding symmetry operations in the algebraic form as augmented

matrices (see

Figure

1.51).

Symmetry

through

element

0,0,0 0,0,0

through

0,0,0 0,0,0

through

0,0,0

and

orientation

First

x,Y, z

symmetry

1 0 0 0

operation

0100

0010

0001

Second

-Y, X-Y, z

-y, x-y, z -y, x-y, '13+z -y, X-y, z

0-1

ool

[-lo

1-100

1-100 1-100

00 10

001113 00 10

0001

0001 0001

-x+y, -x, z -X+~,-X,~/~+Z -x+y, -x, z

symmetry

-1

0 0

operation

1-100

0 0 10

0 0 01

Third

-x+y, -x, z

operation

Fourth

-31,

-Y,

operation

Fifth

x-Y, x,

symmetry

1 -1 0 0

operation

0 0 10

0 0

x-y, x, -z

1-100

I;:;!

Sixth

Y, -x+Y, z y, -x+y,

-z

symmetry

0 1 0 0

operation

-1100

0010

0 001

86 Chapter

Even though the column (Table 1.19) and the row (Table 1.20) labeled

"First symmetry operation" seem redundant, their presence highlights the

fact that each symmetry element contains one-fold rotation or unity

operation. Furthermore, as easy to see from these tables, four-fold rotation

axes also contain the two-fold symmetry operation

(e.g. the third symmetry

operation for 4

is the same as the second symmetry operation for

and six fold rotation axes contain both three- and two-fold rotations (e.g.

second and third symmetry operations for

are identical to second and

third for

while the fourth symmetry operation for 6

is identical to

the second for

Z).

1.20.7

Interactions between symmetry operations

We now consider how the two interacting symmetry operations produce a

third symmetry operation, similar to how it was described in section 1.6 but

now in terms of their algebraic representation. Assume that two symmetry

operations, which are given by the two augmented matrices

and A', are

applied in sequence to a point, coordinates of which are represented by the

augmented vector V. Taking into account Eq. 1.48, but written in a short

form, the first symmetry operation will result in the vector

given as

The second symmetry operation applied to the vector

will result in the

third vector,

as follows

Recalling, that the associative law holds for symmetry operations and for

symmetry groups (see sections 1.6 and

1.7),

equation 1.50 can be rewritten

It follows from Eq. 1.51 and from our earlier consideration of

interactions between symmetry elements, finding which symmetry operation

appears as the result of consecutive application of any two symmetry

operations is reduced to calculating the product of the corresponding

augmented matrices. To illustrate how it is done in practice, consider Figure

1.16 and assume that the two-fold axis is parallel to

The corresponding

symmetry operations,

and At, are (Table 1.19):

Fundamentals

crystalline state

The presence of the center of inversion introduces one additional

symmetry operation,

It is easy to see that the product of

and

is the fourth symmetry

operation,

A~, which is nothing else but the mirror reflection in the plane,

which is perpendicular to

and passes through the origin of coordinates:

All other products between the four matrices do not result in new

symmetry operations, i.e.

now we know quite well that this combination of symmetry

operations corresponds to point group symmetry 2/m (also see

Figure

1.46).

Chapter

1.21

Non-conventional symmetry

Conventional crystallography was developed using the explicit

assumption that crystalline objects maintain ideal periodicity in three

dimensions. As a result, any ideal three-dimensional crystal structure can be

described using a periodic lattice and one of the 230 crystallographic space

groups (see section 1.16). The overwhelming majority of both naturally

occurring and synthetic crystalline solids are indeed nearly ideal. Their

diffraction

patterns are perfectly periodic since Bragg peaks are only

observed at the corresponding points of the reciprocal lattice, which reflects

both the symmetry and three-dimensional periodicity of the crystal lattice.

Long ago the first aperiodic crystal was reported,' and the apparent absence

of the three-dimensional periodicity of diffraction patterns was later found in

a number of materials. One of the most prominent examples is the 1984

discovery of the five-fold symmetry in the diffraction pattern of rapidly

cooled A10.86Mn0.14 alloy.2 Supported by many experimental observations,

several approaches to describe the symmetry of aperiodic structures have

been developed and successfully used to establish the crystal structure of

these unusual materials.

Probably the most fruitful method has been suggested by

P.M.

de Wolff

in which more than three physical dimensions are used to represent the

crystal lattice and thus to restore its periodicity in the so-called superspace.

Then the resulting aperiodic diffraction pattern is simply a projection of the

crystal lattice, which is periodic in the superspace, upon the physical space,

which is three-dimensional. The diffraction pattern of an aperiodic crystal

usually contains a subset of strong

(i.e. highly intense) diffraction peaks,

which are called main peaks, and their indices are described using three

integers corresponding to a standard three-dimensionally periodic crystal

lattice. The subsets of the so-called satellite peaks are weaker and their

indices include more than three integers to reflect the increased

dimensionality of the superspace (see the footnote on page 401).

1.21.1

Commensurate modulation

Consider the simplest case, when the periodicity of the crystal lattice is

perturbed in one dimension by periodic deviations of atoms from their ideal

Dehlinger, iiber die Verbreiterung der Debyelinien bei kaltbearbeiteten Metallen,

Kristallogr.

65,

927).

Shechtman,

Blech, D. Gratias and J.W. Cahn, Metallic phase with long-range

orientational order and no translational symmetry, Phys. Rev. Lett.

53,

195

(1984).

P.M. de Wolff, The pseudo-symmetry of modulated crystal structures, Acta Cryst.

A30,

777

(1 974).

Fundamentals

crystalline state 89

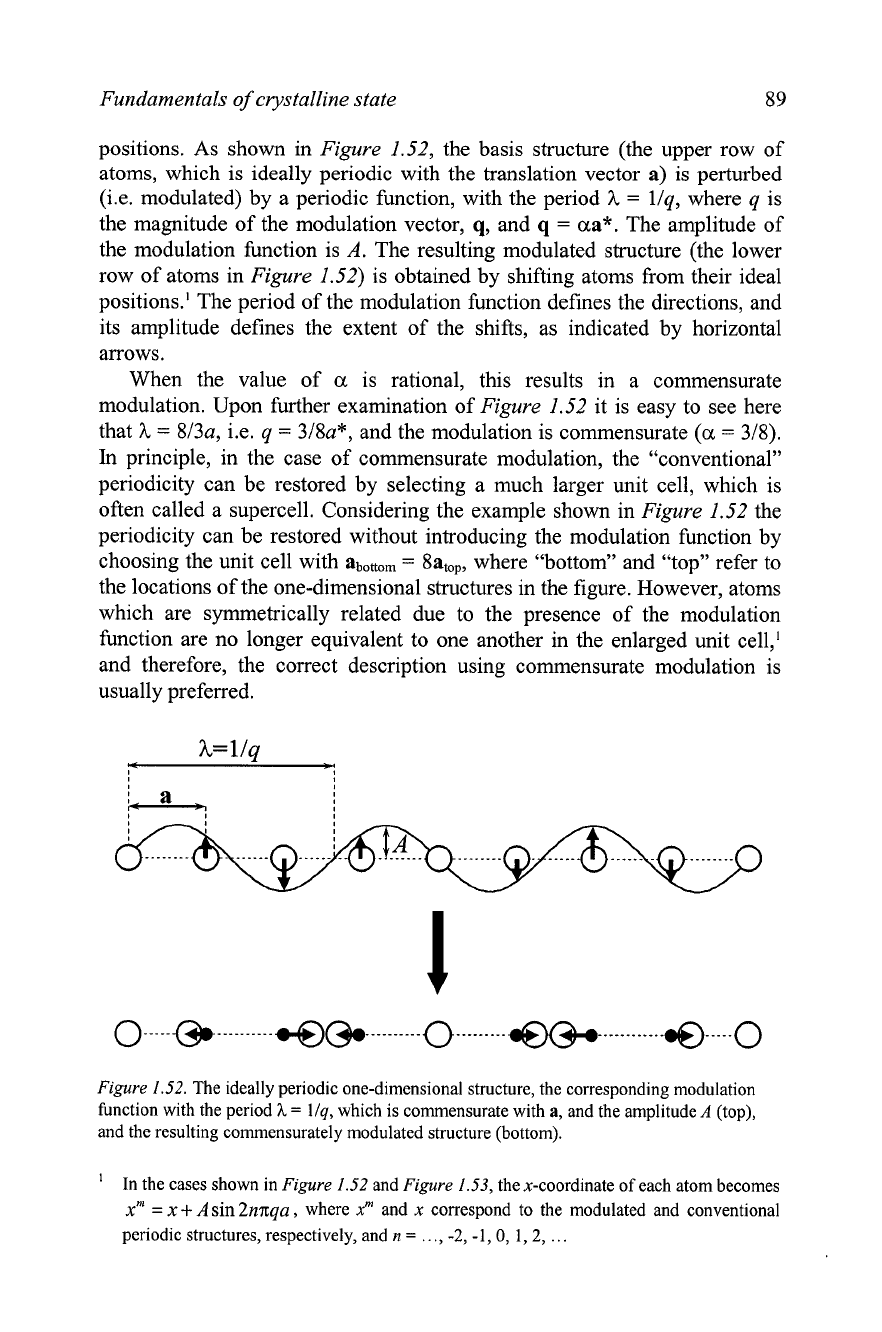
positions. As shown in Figure 1.52, the basis structure (the upper row of

atoms, which is ideally periodic with the translation vector a) is perturbed

(i.e. modulated) by a periodic function, with the period

llq, where q is

the magnitude of the modulation vector, q, and q

aa*. The amplitude of

the modulation function is

The resulting modulated structure (the lower

row of atoms in Figure 1.52) is obtained by shifting atoms from their ideal

position^.^

The period of the modulation function defines the directions, and

its amplitude defines the extent of the shifts, as indicated by horizontal

arrows.

When the value of

is rational, this results in a commensurate

modulation. Upon further examination of Figure 1.52 it is easy to see here

that

8/3a, i.e. q

318a*, and the modulation is commensurate (a

318).

principle, in the case of commensurate modulation, the "conventional"

periodicity can be restored by selecting a much larger unit cell, which is

often called a supercell. Considering the example shown in Figure 1.52 the

periodicity can be restored without introducing the modulation function by

choosing the unit cell with

abottom

8atop, where "bottom" and "top" refer to

the locations of the one-dimensional structures in the figure. However, atoms

which are symmetrically related due to the presence of the modulation

function are no longer equivalent to one another in the enlarged unit

cel1,l

and therefore, the correct description using commensurate modulation is

usually preferred.

Figure

1.52.

The ideally periodic one-dimensional structure, the corresponding modulation

function with the period

llq,

which is commensurate with

and the amplitude

(top),

and the resulting commensurately modulated structure (bottom).

In the cases shown in

Figure

1.52

and

Figure

1.53,

thex-coordinate of each atom becomes

xn'

sin

2nnqa,

where xm and x correspond to the modulated and conventional

periodic structures, respectively, and

-2,

-1,0,

1,2,