Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

1.4. Комментарии к библиографии 51

TЦATГЦ,

TЦATГЦA,

TЦATГЦAЦ,

TЦATГЦAЦT,

TЦATГЦAЦTГ,

TЦATГЦAЦTГЦ,

TЦATГЦAЦTГЦГ.

Значит, исходная молекула α есть 3

-АГТАЦГТГАЦГЦ.

Еще раз подчеркнем, что наше описания весьма упрощены.

Например, в процедуре секвенирования, описанной выше, есть

много деликатных моментов. Так, используемая полимераза

не должна иметь эндонуклеазной активности — в противном

случае она могла бы отрезать дидезоксинуклеотиды, останав-

ливающие комплементарный синтез на матрице. Обычно здесь

применяют так называемый Кленов-фрагмент ДНК полимера-

зы I. Далее, количество дидезоксинуклеотидов в пробирках А,

Т, Ц, Г должно выбираться весьма аккуратно. Если их будет

слишком много, то полимераза может прекратить работу еще

внутри собственной приставки секвенируемой молекулы, так

как вероятность дойти до конца матрицы уменьшается с ро-

стом концентрации дидезоксинуклеотидов.

Наконец, через гель можно прогонять только не слишком

длинные молекулы. Одн ако длинную молекулу можно разбить

на перекрывающиеся фрагментов меньшей длины. Зная нук-

леотидную последовательность каждого из этих фрагментов и

то, как они перекрываются, можно восстановить нуклеотидную

последовательность всей молекулы.

1.4 Комментарии к библиографии

Имеется очень много хороших книг по молекулярной биологии

и генетической инженерии, ориентированных на читателей с

различным уровнем подготовки.

Книга Дрлика [76] — прекрасное введение в молекулярную

биологию и генетическую инженерию. Она не требует от чи-

52 1. Как устроена ДНК и как с ней работают

тателя никакой подготовки ни в биохимии, ни в биологии (на-

ше «стерженьковое» изображение нуклеотидов заимствовано

из этой книги). Изящным и про стым введением в генет иче-

скую инженерию является также книга [316], хотя кое-что в

ней уже устарело. Книга [70], также написанная для неподго-

товленного читателя, дает более эскизную картину, но удобна,

когда нужно быстро получить какую-либо справку.

Книга Албертса и соавторов [8] — стандартный учебник мо-

лекулярной биологии, который может быт ь использован и как

обстоятельный справочник. Книга Уокера и Рэпли [330] следу-

ет новой концепции в учебной литературе, согласно которой чи-

татель получает возможность самостоятельно определ ять по-

следовательность изучения интересующих его тем. Это — пре-

красное справочное издание. Мы особо рекомендуем эту книгу

тем читателям, которые, прочитав ряд более популярных книг

по молекулярной биологии и генетической инженерии, хотели

бы как-то упорядочить полученную ими информацию.

Глава 2

Начала молекулярных вычислений

2.1 Опыт Эдлмана

«Нам видна только ближайшая перспектива, но и там мы ви-

дим много задач, требующих решения». Эти слова Тьюрин-

га [324], которые, конечно, приложимы к любой развивающей-

ся науке, удачно характеризуют основополагающие принципы

исследовательских программ в области компьютерных наук.

Прорывы в компьютерных науках часто проявляются и запо-

минаются благодаря неожиданным демонстрациям, а не реша-

ющим экспериментам, как то бывает в физике. Как отмеча-

ет Хартманис [127], роль таких демонстраций состоит в том,

что они показывают принципиальную или практическую осу-

ществимость того, что ранее представлялось н евозможным или

практически нереализуемым. Зачастую идеи и понятия, рож-

денные и испытанные в этих демонстрациях, определяют «по-

вестку дня» в компьютерных науках или, по меньшей мере,

существенно влияют на нее. Опыт Эдлмана [2] как раз и пред-

ставляет собой такого рода демонстрацию. Данная книга по-

священа той ближайшей перспективе, которая нам видна, и

той теории, которая уже развита применител ьно к различным

аспектам молекулярных вычислений. К чему в конце концов

приведет идея «ДНК-компьютера», пока еще неясно; мы про-

должим обсуждение возможных перспектив в разделе 2.4.

Еще тогда, когда было принято именовать компьютер «ги-

гантским мозгом» и когда только нечто, не уступающее раз-

мерами по меньшей мере комнате, могло соотв етствова ть ви-

зуальному образу мощной вычислительной машины, был сде-

лан ряд пророческих замечаний о возможной в будущем ми-

ниатюризации. Часто цитируется предвидение Фейнмана [89],

описавшего еще в 1959 г. возможность построения «суб-микро-

54 2. Начала молекулярных вычислений



























1











*









>



=



Рис. 2.1. Граф в опыте Эдлмана.

скопических» компьютеров. С тех пор в миниатюризации ком-

пьютеров был достигнут замечательный прогресс, но до суб-

микроскопического уровня пока еще далеко. Были предложе-

ны и широко обсуждаются два направления дальнейшего про-

движения: квантовые и молекулярные вычисления. Опыт Эдл-

мана, к описанию которого мы п рист упаем, послужил выра-

зительной демонстрацией возможностей молекулярного подхо-

да. Чтобы оставаться на почве реал ьности , мы разберем здесь

именно пример, приведенный в [2].

В опыте Эдлмана решалась задача о гамильтоновом пути

для данного ориентированного графа. Мы рассмотрим эту за-

дачу в следующей формулировке. Пусть G — ориентированный

граф с выделенными начальной и конечной вершинами v

out

. Путь из v

в v

out

называется гамильтоновым, если он

проходит через каждую вершину в точности один раз. (Это, в

частности, влечет, что v

6= v

out

, поскольку в противном слу-

чае вершина v

= v

out

встретилась бы в пути дважды.)

Например, у графа, изображенного на рис. 2.1, выделены

начальная вершина 0 и конечная вершина 6. Путь, состоящий

из направленных ребер 0 −→ 1, 1 −→ 2, 2 −→ 3, 3 −→ 4,

4 −→ 5, 5 −→ 6, является гамильтоновым.

2.1. Опыт Эдлмана 55

Мы пронумеровали вершины так, что гамильтонов путь

проходит через них по порядку. Разумеется, если найден га-

мильтонов путь, то такую нумерацию всегда можно выбрать.

В нашем частном примере оказывается, что вышеупомянутый

путь является единственным гамильтоновым путем. Действи-

тельно, н етрудно перебрать все имеющиеся возможности.

Первый шаг 0 −→ 3 приводит к путям 0 −→ 3, 3 −→ 2, 2 −→ 1;

0 −→ 3, 3 −→ 4, 4 −→ 1, 1 −→ 2 и 0 −→ 3, 3 −→ 4, 4 −→ 5,

5 −→ 2, 2 −→ 1, которые уже нельзя продолжить, не повторив

какую-либо вершину, и к пути 0 −→ 3, 3 −→ 4, 4 −→ 5, 5 −→ 6.

Точно так же сразу видно, что и первые шаги 0 −→ 1, 1 −→ 3

и 0 −→ 6 не приводят к успеху. Этот аргумент показывает

также, что если удалить любое из ребер пути 0 −→ 1, 1 −→ 2,

2 −→ 3, 3 −→ 4, 4 −→ 5, 5 −→ 6, то у остающегося графа

нет гамильтоновых путей. Ясно и то, что есл и взять в каче-

стве начальной какую-либо вершину, кроме 0, или в качестве

конечной какую-либо вершину, кроме 6, то получающийся

граф (с теми же ребрами) не имеет гамильтонова пути. Это

следует из того, что ни одно ребро не заходит в вершину 0 и

не выходит из вершины 6.

В общем случае задача о гамильтоновом пути, ЗГП, заклю-

чается в определении того, обладает ли произвольно заданный

граф гамильтоновым путем. Очевидно, что ЗГП может быть

решена п утем полного перебора. Для решения ЗГП были раз-

виты различные алгоритмы. Хотя эти алгоритмы успешно ра-

ботают для некоторых специальных классов графов, все они,

будучи применены к общим ор иент иров анн ым графам, дают

экспоненциальную сложность в наихудшем случае. Это зна-

чит, что в общем случае все и звестные алгоритмы так или

иначе сводятся к исчерпывающему перебору. В действитель-

ности известно, что задача о гамильтоновом пути NP-полна,

что означает, что для нее вряд ли существует эффективный

(т. е. дающий ответ за полиномиальное время) алгоритм. ЗГП

труднорешаема в том смысле, что нахождение ответа для гра-

фа умеренных размеров может потребовать нереального коли-

чества компьютерного времени. В своем опыте Эдлман решил

56 2. Начала молекулярных вычислений

ЗГП для вышеприведенного примера, в котором граф мал с

любой точки зрения. Однако его подход применим, по крайней

мере в принципе, и к б´ольшим гр афам. Ключами к решению

служат массированный па раллелизм и комплементарность.

Подход Эдлмана основан на следующем недетерминирован-

ном алгоритме для решения ЗГП.

Вход. Ориентированный граф G с n вершинами, среди которых

выделены вершины v

и v

out

Шаг 1. Породить большое количество случайных путей в G.

Шаг 2. Отбросить пути, которые не начинаются с v

или не

кончаются в v

out

Шаг 3. Отбросить пути, которые не содержат точно n вершин.

Шаг 4. Для каждой из n вершин v отбросить пути, которые не

содержат v.

Выход. «Да», если останется хоть один путь, «Нет» в против-

ном случае.

По существу этот алгоритм несет в себе полный перебор. В

подходе Эдлмана нежелательный недетерминизм обходится за

счет массированного параллелизма цепочек ДНК. Комплемен-

тарность Уотсона–Крика используется, чтобы обеспечить по-

строение таких последовательностей ребер, которые действи-

тельно являются путями в графе G. Рассмотрим теперь опыт

Эдлмана более детально.

Каждой вершине i графа сопоставляется выбранная слу-

чайным образом цепочка ДНК из 20 нуклеотидов, обознача-

емая через s

, 0 6 i 6 6. Например, для i = 2, 3, 4 Эдлман

использовал следующие олигонуклеотиды длины 20:

= TATЦГГATЦГГTATATЦЦГA,

= ГЦTATTЦГAГЦTTAAAГЦTA,

= ГГЦTAГГTAЦЦAГЦATГЦTT.

Что касается ориентации, то все эти нуклеотиды записаны в

направлении от 5

к 3

2.1. Опыт Эдлмана 57

Удобно использовать функцию h, отображающую каждое

из оснований ДНК на его дополнение по Уотсону–Крику:

h(A) = T, h(T) = A, h(Ц) = Г, h(Г) = Ц.

На цепочки ДНК h действует побуквенно:

h(ЦATTAГ) = ГTAATЦ.

Таким образом, h дает дополнение по Уотсону–Крику для ис-

ходной цепочки. При этом h изменяет ориентацию следующим

образом: если исходная цепочка была записана в направлении

от 5

к 3

, то ее дополнение по Уотсону–Крику будет записано

в направлении от 3

к 5

. В терминологии теории формальных

языков (подробно описанной в главе 3) отображение h являет-

ся морфизмом. Мы будем называть его морфизмом Уотсона–

Крика. Например,

h(s

) = ATAГЦЦTAГЦЦATATAГГЦT,

h(s

) = ЦГATAAГЦTЦГAATTTЦГAT.

Разложим теперь каждую цепочку s

, 0 6 i 6 6, на две

цепочки длины 10: s

= s

. Таким образом, на s

(соответ-

ственно на s

) можно смотреть как на первую (соответственно

вторую) половину цепочки s

. Ребро, идущее из вершины i в

вершину j (в случае, если таковое имеется в графе G), кодиру-

ется цепочкой h(s

). Итак, ребро также кодируется 20-мером,

который возникает как дополнение по Уотсону–Крику второй

и первой половин олигонуклеотидов, кодирующих смежные с

этим ребром вершины. Вот коды трех конкретных ребер:

2→3

= ЦATATAГГЦTЦГATAAГЦTЦ,

3→2

= ГAATTTЦГATATAГЦЦTAГЦ,

3→4

= ГAATTTЦГATЦЦГATЦЦATГ.

Заметим, что эта конструкция сохраняет ориентацию ребер:

олигонуклеотиды e

2→3

и e

3→2

совершенно различны.

Мы готовы описать главную фазу опыта Эдлман а. Для

каждой вершины i и для каждого ребра i −→ j исходного

графа были взяты большие количества олигонуклеотидов s

и e

i→j

, которые затем были смешаны вместе и участвовали в

58 2. Начала молекулярных вычислений

одной реакции сшивки. Олигонуклеотиды s

служили скреп-

ками, благодаря которым могли сшиваться олигонуклеотиды,

соответствующие смежным ребрам. Следовательно, реакция

сшивки приводила к образованию таких молекул ДНК, ко-

торые можно считать кодами случайных путей в исходном

графе. (Эдлман использовал также определенные лигазы и

выдерживал всю смесь 4 часа при комнатной температуре.

Для читателей, знакомых со статьей Эдлман а [2], упомянем

небольшие р азли чия в наших обозначениях. Мы поместили в

«бульон» олигонуклеотиды s

, в то время как Эдлман поме-

щал туда олигонуклеотиды h(s

). Соответствующие изменения

касаются и олигонуклеотидов e

i→j

Объем реакции сшивки в опыте Эдлмана намного превос-

ходил тот, что был необходим для графа такого размера. Дей-

ствительно, для каждого ребра в бульоне присутствовало по-

рядка 10

копий коди рующего олигонуклеотида. Это значит,

что, по всей вероятности, возникало много молекул ДНК, коди-

рующих гамильтонов путь, хотя уже наличие одной-единствен-

ной такой молекулы доказывало бы существование гамильто-

нова пути. Другими словами, весьма вероятно, что достаточ-

ным было бы существенно меньшее количество олигонуклеоти-

дов, чем то, что использовал Эдлман, или что с помощью ис-

пользованного им количества олигонуклеотидов могли бы быть

исследованы намного б´ольшие графы.

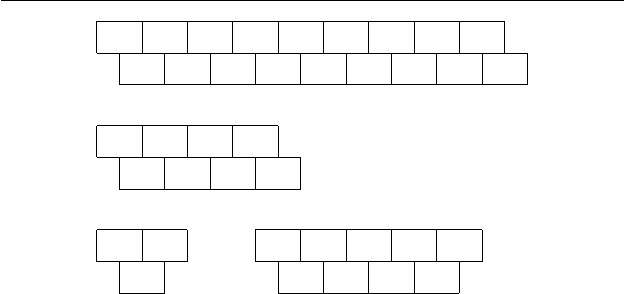
Для иллюстрации мы изобразили на рис. 2.2 некоторые це-

почки ДНК, которые могли возникать в ходе опыта. Мы ис-

пользуем введенн ые выше обозначения s

и e

i→j

. Отметим, что

эти двойные цепочки имеют открытые концы.

Вернемся к недетерминированному алгоритму, состоящему

из четырех описанных выше шагов. Мы уже объяснили, как

можно осуществить Шаг 1. Остающиеся шаги, так же, как и

заключение на выходе, суть процедуры фильтрации или скри-

нинга, в которых участвуют биохимические технологии, выхо-

дящие за рамки данной книги. (Заинтересованный читатель

может найти детали в [2]. Например, Шаг 2 может быть реа-

лизован с помощью применения к продукту, полученному на

2.1. Опыт Эдлмана 59

1→3

3→4

4→1

1→2

2→3

3→4

4→5

5→2

2→3

0→3

3→2

2→1

1→3

0→6

0→3

3→4

4→5

5→6

Рис. 2.2. Примеры путей в графе Эдлмана.

Шаге 1, полимеразной цепной реакции (ПЦР) с праймерами

h(s

) и s

. Это означает, что будут размножены лишь молеку-

лы, кодирующие пути с началом в вершине 0 и концом в 6.)

С нашей точки зрения следующие рассмотрения важнее,

чем описания процедур фильтрации, основанных на биохими-

ческих технологиях. О пыт Эдлмана занял примерно 7 лабора-

торных дней. Больше всего времени ушло на процедуру филь-

трации на Шаге 4. Не следует, однако, спешить с негативными

выводами из того, что с таким маленьким примером пришлось

провозиться так долго. Молекулярный алгоритм, использован-

ный в опыте, был весьма примитивным и малоэффективным.

Как и для традиционных компьютеров, оптимизация алгорит-

мов может расширить область применимости метода. В част-

ности, с точки зрения теории графов далеко не оптимальной

идеей представляется использование всех олигонуклеотидов в

равном количестве. Это приводит, например, к образованию

большого числа молекул, кодирующих пути, которые либо не

начинаются в вершине 0, либо не оканчиваются в вершине 6.

Следует сперва подсчитать поток через граф и использовать

полученные результаты, чтобы определить, в каком количестве

потребуется каждый олигонуклеотид.

В общем случае определить или даже оценить оптималь-

ное количество каждого нуклеотида довольно сложно. Здесь

60 2. Начала молекулярных вычислений

возникают весьма трудные задачи теории графов. Интуитивно

ясно, что количество каждого нуклеотида должно быть доста-

точным, чтобы обеспечить высокую вероятность возникнове-

ния молекулы, кодирующей гамильтонов путь (при условии,

что таковой существует). Отсюда следует, что это количество

должно расти экспоненциально с ростом числа вершин.

Еще одна возможность для оптимизации кроется в выбо-

ре длины олигонуклеотидов, используемых дл я кодирования.

Эдлман выбрал 6 случайных 20-меров из общего числа 4

. Та-

кой случайный выбор снизил вероятность того, что у олигону-

клеотидов, соответствующих различным вершинам, окажутся

длинные общие подпоследовательности, которые могли бы вы-

звать «нежелательные» соединения в процессе сшивки. Выбор

20-меров гарантировал, что при образовании двойных цепочек

из олигонуклеотидов, кодирующих вершины и ребра, задей-

ствованы 10 нуклеотидных пар, благодаря чему связь была

устойчивой пр и комнатной температуре. Для б´ольших графов,

возможно, понадобятся более длинные олигонуклеотиды.

Как уже отмечалось, весьма вероятно, что в о пыте Эдлма-

на возникало много молекул ДНК, кодирующих гамильтонов

путь. Процедуру скрининга на выходе алгоритма можно мо-

дифицировать таким образом [2], чтобы она возвращала явное

описание гамильтонова пути (или одного из таких путей в слу-

чае, когда их несколько ). Ясно, что подход Эдлмана обладает

большим потенциалом для дальнейшего р азвити я и модифика-

ций. Рассмотрим, например, хорошо известную задачу комми-

вояжера. Она состоит в нахождении кратчайшего гамильтоно-

ва пути в ориентированном графе, ребрам которого приписа ны

длины. Соответствующая модификация могла бы состоять в

кодировании информации о длине путей с помощью использо-

вания олигонуклеотидов различной длины. Заключительный

скрининг должен тогда обнаруживать кратчайший р езультат

(соответствующий кратчайшему гамильтонову пути).

В завершение раздела мы дадим абстрактную формулиров-

ку ключевых моментов опыта Эдлмана. Эта абстрактная фор-