Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений
Подождите немного. Документ загружается.


2.2. Решение задачи о выполнимости и взлом DES 71
логических основ указанных операций. Можно принять и
другую точку зрения, не апеллирующую к безошибочным
операциям. Если начальная пробирка содержит много копий
каждой интерпретации, то хотя некоторые из них могут быть
потеряны, вероятность все же получить правильный ответ
будет достаточно велика.
В качестве еще одного примера р ассмотри м пропозицио-
нальную формулу δ. Формула β, рассмотренная выше, не пока-
зательна по двум причинам. Во-первых, все переменные появ-
ляются во всех дизъюнктах. Во-вторых, β имеет слишком мало
дизъюнктов даже по отношению к малому числу переменных.
(Формула с малым числом дизъюнктов выполнима независи-
мо от самих дизъюнктов; несложно указать соответствующие
нижние границы.) Хотя формула δ все еще не слишком велика
и ее выполнимость может быть обнаружена без особых труд-
ностей, она лишена этих двух недостатков.
Формула δ имеет 5 переменных и 11 дизъюнктов:
δ = (∼ x
1
∨ ∼ x
2
∨ ∼ x
3
) ∧ (x
1
∨ x
2
∨ ∼ x
4
) ∧ (∼ x
1
∨ x
2
∨ x
4
)
∧(x
1
∨ x
2
∨ ∼ x
5
) ∧ (x
1
∨ ∼ x
2
∨ ∼ x
5
) ∧ (x
1
∨ x
3
∨ x
4
)
∧(∼ x
1
∨ x
3
∨ ∼ x
5
) ∧ (x
1
∨ ∼ x
4
∨ x
5
) ∧ (x
2
∨ ∼ x
3
∨ x
4
)
∧(x
3
∨ x
4
∨ x
5
) ∧ (x
3
∨ ∼ x
4
∨ x
5
).
Начальная пробирка N
0
содержит все 32 возможные интер-
претации: 00000, 00001, . . . , 11111. Следующая таблица описы-
вает содержимое пробирок N
0
, N
1
, . . . , N
11
в ходе описанного
выше процесса. Каждая пробирка N
i
, i = 1, 2, . . . , 11, характе-
ризуется списком исключаемых из N
i−1
цепочек.
Таким о бразом, в конечной пробирке N
11
останутся цепоч-
ки, кодирующие интерпретации 01100, 10110 и 10111, и завер-
шающая операция обнаружить возвратит значение истина.
Изложенный выше метод нетрудно приспособить для ра-
боты с произвольными пропозициональными формулами, не
обязательно приведенными к конъюнктивной нормальной фор-
ме [184]. Каждая такая формула получается применением к
переменным уна рной операции отрицания и бинарных опера-
ций конъюнкции и дизъюнкции. (Можно рассматривать и дру-

72 2. Начала молекулярных вычислений
Пробирка Исключенные цепочки
N
0
ни одна не исключена
N
1
11100, 11101, 11110, 11111
N
2
00010, 00011, 00110, 00111
N
3
10000, 10001, 10100, 10101
N
4
00001, 00101
N
5
01001, 01011, 01101, 01111
N
6
00000, 01000
N
7
10011, 11001, 11011
N
8
01010, 01110
N
9
00100
N
10
11000
N
11
10010, 11010
гие пропозициональные связки, но для наших обсуждений это
несущественно.) Вычислительная сложность описанного про-
цесса определяется числом m бинарных операций, в то время
как количество отрицаний и переменных не имеет значения.
После m + 1 разделений и m слияний получаются две про-
бирки, первая из которых содержит молекулы, пр едставляю-
щие (т. е. кодирующие) интерпретации, при которых формула
выполняется, в то время как вторая содержит молекулы, пред-
ставляющие все пр очи е интерпретации. Таким образом, задача
о выполнимости решается однократным применением к первой
пробирке операции обнаружить.
При анализе физических препятствий на пути к созданию
практически пригодного молекулярного компьютера следует
сконцентрировать вни мание на возможных реализациях раз-
личных операций. С помощью операций, рассмотренных нами,
легко писать программы, но вопрос о том, насколько легко их
реализовать на практике, относится к сфере микробиологиче-
ских технологий. Сколько-нибудь детальное обсуждение таких
технологий выходит за рамки данной книги, и мы ограничимся
несколькими общими замечаниями.
Естественный способ реализовать операцию слить — влить
содержимое одной пробирки в другую. Интуит ивн о кажется,

2.2. Решение задачи о выполнимости и взлом DES 73
что такая операция выполнима быстрее и с меньшей вероят-
ностью ошибки, чем операция разделить, которая несомненно
требует гораздо более тонких методов. Последнее верно и по
отношению к операции обнаружить, однако, представляет-
ся, что в стандартных программах операция обнаружить
производится редко. Следовательно, то, как реализуется эта
операция, не слишком сильно влияет на вычислительную
сложность процесса, хотя величина ее погрешности, конечно,
очень важна. Реализация операции разделить может приво-
дить как к ошибкам включения, так и к ошибкам исключения.
В первом случае цепочка, которая до лжн а попасть в пробирку
+(N, w), в действительности оказывается не там, а возмож-
но, даже в −(N, w). Аналогично, при ошибке исключения
цепочка, которая должна оказаться в пробирке −(N, w), туда
не попадает. Было бы полезным изучить различия в вероят-
ностях ошибок этих двух т ипов . В разделе 2.4 мы обсудим
еще ряд вопросов, связанных с осуществимостью операций и
погрешностями при их выполнении.
В оставшейся части этого раздела мы рассмотрим модель
молекулярных вычислений, которая была введена в [291] и на-
звана там стикерной моделью. Мы также обсудим основанный
на этой модели метод взлома широко используемой крипто-
системы DES (Data Encryption Standard), см. [6]. Стикерная
модель базируется на парадигме комплементарности Уотсона–
Крика, благодаря которой цепочки ДНК можно использовать
как физический носитель инфо рмаци и. По существу, стикер-
ная модель есть память с произвольным доступом, причем не
требующая удлинения цепочек и допускающая, по крайней ме-
ре теоретически, многократное использование.
Прежде всего, опишем основанный на комплементарно-
сти метод представления информации цепочками ДНК. В
этом методе используется два основных типа одноцепочечных
молекул ДНК: запоминающие цепочки и цепочки-наклейки
или стикеры. Запоминающая цепочка длиной n нуклеотидов
содержит k неперекрывающихся подцепочек, каждая из ко-
торых имеет длину m нуклеотидов. Таким образом, должно
74 2. Начала молекулярных вычислений
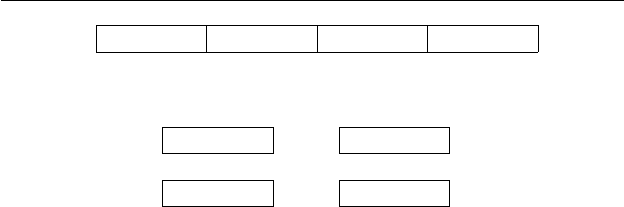
запоминающая цепочка
наклейки
Г Г Г Г Г
Т Т Т Т Т Ц Т Ц Т Ц
А А А А Г
Г А Г А Г Т Т Т Т Ц А А А А А Ц Ц Ц Ц Ц
. . .. . .
Рис. 2.5. Пример стикерной памяти.
выполняться неравенство n > mk. На п ослед ующих иллюстра-
циях подцепочк и изображаются вплотную примыкающими
друг к другу, хотя в действительности такое ограничение и
не является необходимым. В ходе вычи слени я каждая подце-
почка представляет одну фиксированную б улеву переменную
(или, что эквивалентно, один бит). Подцепочки должны суще-
ственно отличаться одна от другой: в любых двух из них по
крайней мере на нескольких позициях должны стоять разные
нуклеотиды. Это нужно для того, чтобы каждый бит мог
быть с уверенностью идентифицирован. Каждый стикер имеет
длину m нуклеотидов и комплементарен в точности одной из
k подцепочек запоминающей цепочки.
Каждая подцепочка запоминающей цепочки может быть
либо включена, либо выключена. Говорят, что подцепочка
включена, если к ней присоеди нен соответствующий ей стикер.
В противном случае, если к подцепочке не присоединен стикер,
говорят, что она выключена. Термин запоминающий комплекс
будет использоваться для запоминающих цепочек, в которых
включены некоторые подцепочки. Запоминающие комплексы
представляют числа в двоичной записи : включенные (соот-
ветственно выключенн ые) подцепочки представляют цифру 1
(соответственно 0). Итак, запоминающие комплексы — это
частично сдвоенные цепочки ДНК.
На рис. 2.5 и зображена запоминающая цепочка дли ны n =
20, разделенная на k = 4 участков дл ино й m = 5. Комплек-
2.2. Решение задачи о выполнимости и взлом DES 75
Г А Г А Г Т Т Т Т Ц А А А А А Ц Ц Ц Ц Ц
Ц Ц Ц Ц ЦА А А А АТ Т Т Т ЦГ А Г А Г
А А А А Г
Г А Г А Г
Ц Т Ц Т Ц
Т Т Т Т Ц А А А А А Ц Ц Ц Ц Ц
Г Г Г Г Г
Ц Ц Ц Ц Ц
Г Г Г Г ГТ Т Т Т Т
А А А А АТ Т Т Т ЦГ А Г А Г
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
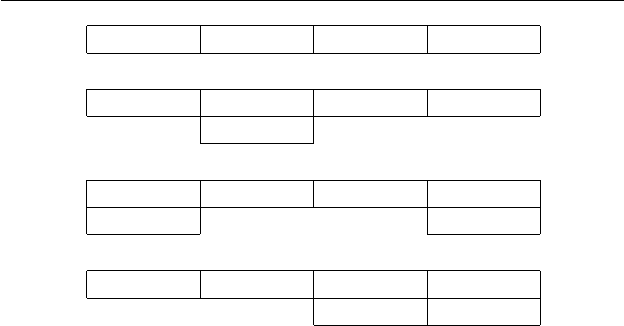
Рис. 2.6. Пример запоминающего комплекса.
сы, получаемые из этой цепочки, можно интерпретировать как
вместилища для четырех битов информации. Рассмотрим, на-
пример, четыре запоминающих комплекса на рис. 2.6. В первом
из них все подцепочки выключены, а в четвертом включены
две последних подцепочки. Двоичные чи сла, представленные
этими четырьмя запоминающими комплексами, суть соответ-
ственно 0000, 0100, 1001 и 0011.
В запоминающей цепочке, приведенной на рис. 2.5, участки,
отвечающие нечетным (соответственно четным) битам состоят
целиком из пуринов (соответственно пиримидинов). Такой вы-
бор имеет то преимущество, что между кодирующими подце-
почками создаются естественные границы. Другими словами,
стикер не может присоединиться к участку, перекрывающему-
ся с двумя выбранными подцепочками. (Такое присоединение
привело бы к ошибке при выполнении описываемых н иже опе-
раций.) В действительности, для любого серьезного примене-
ния стикерной модели важно тщательное изучение наиболее
подходящего кодирования с целью так скомбинировать микро-
биологическую реализуемость и теоретические преимущества,
чтобы достичь оптимального компромисса между ними.
Полезно также сравнить основные структуры данных в
опыте Эдлмана и в стикерных системах и, в частности, идею

76 2. Начала молекулярных вычислений
конструирования двойных цепочек. В обоих случаях сраба-
тывает парадигма комплементарности. В стикерных системах
начинают с длинной одинарной цепочки, к которой присоеди-
няются короткие стикеры, создавая запоминающий комплекс,
т. е. частично сдвоенную цепочку. В опыте же Эдлмана (как
и в решении Липтона задачи о выполнимости) начинают не с
длинной цепочки, а с коротких одинарных цепочек, которые
соединяются шаг за шагом так, что после каждого шага оста-
ются липкие концы. Получающиеся при этом двойные цепочки
не должны иметь одноцепочечных промежутков.
Можно считать, что плотность информации в обоих слу-
чаях (в стикерных системах и опыте Эдлмана) одинакова и
составляет 1/m би т на нуклеотид. Хотя теоретич еский макси-
мум плотности в представлении информации с помощью ДНК
равен двум битам на нуклеотид, при столь большой плотности
любой молекулярный компьютер, основанный на разделении
молекул, был бы слишком чувствителен к ошибкам.
Теперь мы готовы ввести операции, используемые в стикер-
ных системах. Как и те операции, которые мы рассмотрели
выше, они просты, но достаточно гибк и для реализации весь-
ма общих алгоритмов. Как и ранее, пробирка — это мульти-
множество, элементами которого теперь служат запоминаю-
щие комплексы. (То, какими двумерными структурами данных
в действительности представляются запоминающие комплек-
сы, несущественно для наших обсуждений.) Мы рассматрива-
ем операции слить, разделить, включить и очистить.
Операция слить имеет прежний смысл: две пробирки объ-
единяются в одну. При этом запоминающие комплексы из двух
пробирок на входе без изменений присоединенных к ним стике-
ров переходят в новое мультимножество, являющееся объеди-
нением двух данных.
Операция разделить создает по данной пробирке N и це-
лому числу i, 1 6 i 6 k, две н овых пробирки +(N, i) и −(N, i).
Пробирка +(N, i) (соответственно −(N, i)) состоит из всех
запоминающих комплексов исходной пробирки N , в которых
включена (соответственно выключена) i-я подцепочка.

2.2. Решение задачи о выполнимости и взлом DES 77
Для данной пробирки N и целого i, 1 6 i 6 k, операция
включить создает новую пробирку включить(N, i), в которой
у каждого запоминающего комплекса из N включена i-я подце-
почка. Это означает, что подходящий сти кер присоединяется к
запоминающему комплексу, если i-я подцепочка этого комплек-
са была выключена, но если i-я подцепочка уже была включе-
на, то комплекс не изменяется.
Наконец, для данной пробир ки N и целого i, 1 6 i 6 k, опе-
рация очистить создает новую пробирку очистить(N, i), в
которой у каждого запоминающего комплекса из N выключе-
на i-я подцепочка. Это означает, что соответствующие стикеры
удаляются из тех комплексов, где они имелись.
Вычисление в стикерной модели есть последовательность
операций слить, разделить, включить и очистить. Входом и
выходом вычисления являются пробирки. Чтение вых ода со-
стоит в выделении из итоговой проб ирк и одного запоминающе-
го комплекса и определении присоединенных к нему стикеров,
либо в сообщении, что в этой пробирке нет ни одного запоми-
нающего комплекса.
Вход или начальная пробирка является библиотекой за-
поминающих комплексов. Более строго, (k, l)-библиотека, где
1 6 l 6 k, состоит из запоминающих комплексов с k подце-
почками, последние k − l из которых выключены, тогда как
первые l вкл ючены или выключены всеми возможными спосо-
бами. Таким образом, (k, l)-библиотека, рассматриваемая как
мультимножество, содержит 2
l
различных типов запоминаю-
щих комплексов. Их можно представить бинарными последо-
вательностями вида w0
k−l
, где w — произвольная бинарная по-
следовательность длины l. В начальной пробирке первые l под-
цепочек запоминающих комплексов используются для входных
данных, а остальные k − l подцепочек — для хранения проме-
жуточных данных и результатов.
Вычислительная парадигма, ассоци иро ванн ая со стикерной
моделью, состоит в решении трудных задач путем полного пе-
ребора всех входов длины l. Все возможные 2
l
вариантов об-

78 2. Начала молекулярных вычислений
рабатываются параллельно. Можно сказать, что эта парадиг-
ма составляет суть молекулярных вычислений вообще.
Как и в [291], мы проиллюстрируем стикерную модель на
примере решения задачи о минимальном покрытии, ЗМП. Она
может быть сформулирована следующим образом. По данно-
му конечному множеству S = {1, 2, . . . , p} и конечному набо-
ру {C
1
, . . . , C
q
} подмножеств множества S нужно найти наи-
меньшее подмножество I ⊆ {1, 2, . . . , q} такое, что ∪
i∈I
C
i
= S.
Конечно, полный перебор всех 2
q
подмножеств I решает эту
задачу.
Опишем решение, использующее стикерную модель. Запо-
минающие цепочки состоят из k = p + q подцепочек. Исходная
пробирка N
0
есть (p + q, q)-библиотека. (Следует подчеркнуть,
что широкое применение стикерной модели возможно только
при условии, что уже имеются библиотеки определенных раз-
меров. Построение же запоминающих цепочек с k подцепочка-
ми с ростом k становится все более сложным.)
Обозначим через card(X) мощность множества X, т. е. чис-
ло элементов в X. Элементы множества C
i
, 1 6 i 6 q обозна-
чаются c
j
i
, 1 6 j 6 card(C
i
). Таким образом, каждый элемент
c
j
i
— это целое число от 1 до p.
Запоминающие комплексы в исходной пробирке N
0
со-
ответствуют всевозможным подмножествам I множества
{1, 2, . . . , q}. А именно, первые q участков комплекса, буду-
чи включены или выключены, показывают, какие из чисел
1, 2, . . . , q, принадлежат множеству I, отвечающему данному
комплексу. Последние p участков каждого запоминающего
комплекса M первоначально выключены, а по завершении
вычисления подцепочка с номером q + j, 1 6 j 6 p, оказы-
вается включенной в том и только в том случае, когда число
j принадлежит множеству C
i
для некоторого i из множества
индексов I, отвечающего комплексу M. Для этого с M про-
делываются следующие операции. Мы просматриваем первые
q подцепочек в M. Всякий раз, когда мы встречаем вклю-
ченную подцепочку (пусть она имеет номер i; включенные и
выключенные подцепочки р азлич аются с помощью операции

2.2. Решение задачи о выполнимости и взлом DES 79
разделить), мы включаем те из последних p участков, кото-
рые отвечают числам из C
i
. Просмотрев таким образом все
первые q подцепочек комплекса M, мы проверяем, все ли из
последних p подцепочек включены. Это снова может быть
проделано с помощью операции разделить. Включенность
последних p подцепочек означает, что множество индексов
I, соответствующее комплексу M , действительно является
покрытием множества S = {1, 2, . . . , p}. Таким образом, мы
можем отбросить запоминающие комплексы, не удовлетворя-
ющие этому условию, а среди оставшихся найти минимальное
покрывающее множество.
Очевидно, что описанная процедура приводит к решению
задачи. Однако при стандартной последовательной реализации
вычислений такое решение требует громадных затрат времени:
при q = 100, мы должны применить процедуру для каждого из
2
100
запоминающих комплексов. Положение меняется при ис-
пользовании ДНК-вычислений и стикерной модели, поскольку
при таком подходе одновременно обрабатываются все запоми-
нающие комплексы из исходной пробирки N
0
, в которых вклю-
чена первая подцепочка (и значит, C
1
— одно из множеств в
предполагаемом покрытии множества S). Результат использу-
ется на следующем шаге, где в процесс вовлекаются запоми-
нающие комплексы, в которых включена вторая подцепочка,
и т. д. Таким образом, весь процесс будет состоять не из 2
q
, а
только из q шагов.
Напомним обозначения +(N, i), −(N, i) и включить(N, i),
связанные с операциями разделить и включить. Следующая
простая программа, в которой исходная пробирка N
0
является
(p + q, q)-библиотекой, формализует описанную выше идею:
(1) для i от 1 до q
разделить + (N
0
, i) − (N
0
, i)
для j от 1 до card(C
i
)
включить(+(N
0
, i), q + c
j
i
)
N
0
← слить(+(N
0
, i), −(N
0
, i))

80 2. Начала молекулярных вычислений
(2) для i от q + 1 до q + p
N
0
← +(N
0
, i)
На выходе этой программы получается п роб ирка N
0
, содер-
жащая только те запоминающие комплексы, в которых вклю-
чены все последние p подцепочек. Для того, чтобы решить
ЗМП, следует еще выбрать из N
0
запоминающий комплекс, у
которого среди первых q подцепочек наименьшее число вклю-
ченных. В следующей программе по завершении внешнего цик-
ла на шаге (3) в пробирке N
i
, i > 1 будут находиться все те
запоминающие комплексы, в которых из первых q подцепочек
включены ровно i. Таким образом, на выходе программы по-
лучится решение ЗМП.
(3) для i от 0 до q − 1
для j от i до 0
разделить + (N
j
, i + 1) и − (N
j
, i + 1)
N
j+1
← слить(+(N
j
, i + 1), N
j+1
)
N
j
← −(N
j
, i + 1)
(4) обнаружить N
1
;
если N
1
пуста обнаружить N
2
;
если N
2
пуста обнаружить N
3
;
. . . . . . . . . . . .
При желании читатель может «прокрутить» двойной цикл
в шаге (3) на простом примере. Пусть q = 4 и C
3
покрыва-
ет множест во S вместе с любым другим множеством C
i
, в то
время как C
1
, C
2
, C
4
даже вместе не покрывают S. Это озна-
чает, что в пробирку N
0
к шагу (3) попадут запоминающие
комплексы, представляющие покрытия (1, 3), (2, 3), (3, 4), и
все покрытия, их содержащие. В таблице 2.1 описывается со-
стояние пробирок после каждого шага внешнего цикла.
Заметим, что приведенная процедура не использует опера-
цию очистить. Еще одно, более важное наблюдение состоит в
том, что описанный алгоритм в принципе может быть исполнен
