Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

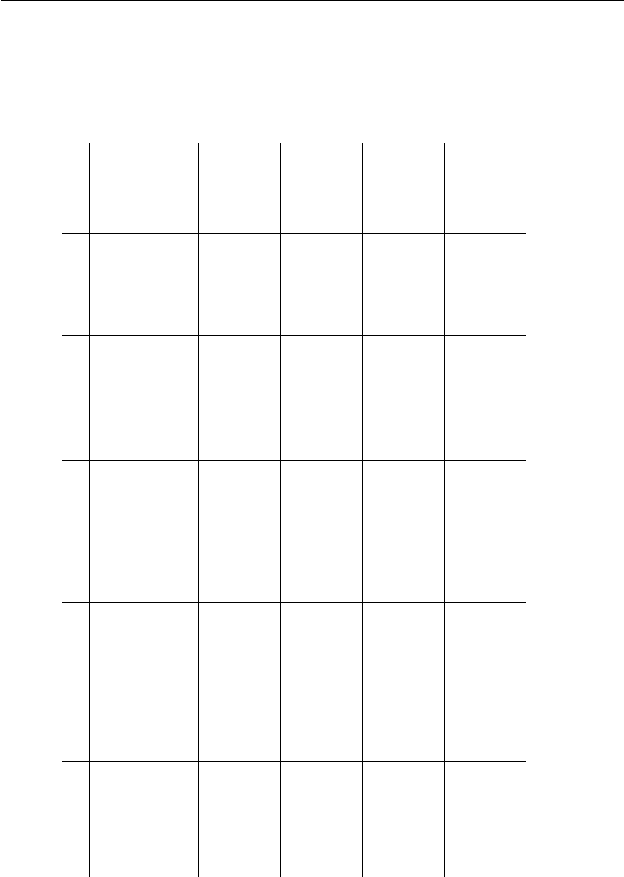
2.2. Решение задачи о выполнимости и взлом DES 81

(1,3),(2,3), пусто пусто пусто пусто

исходное (3,4),(1,2,3),

состояние (1,3,4),(2,3,4),

(1,2,3,4)

i = 0, (2,3),(3,4), (1,3),(1,2,3), пусто пусто пусто

разделить (2,3,4) (1,3,4),

по 1 (1,2,3,4)

i = 1, (3,4) (1,3),(1,3,4), (1,2,3), пусто пусто

разделить (2,3),(2,3,4) (1,2,3,4)

по 2

i = 2, пусто (3,4) (1,3),(2,3), (1,2,3), пусто

разделить (1,3,4), (1,2,3,4)

по 3 (2,3,4)

i = 3, пусто пусто (1,3),(2,3), (1,2, 3), (1,2,3,4)

разделить (3,4) (1,3,4),

по 4 (2,3,4)

Таблица 2.1. Отбор минимального покрывающего множества.

82 2. Начала молекулярных вычислений

роботом, автоматически производящим действия, из которых

складываются вычислительные операции. Для этого необходи-

мо, чтобы эти действия можно было выполнять «вслепую», т.е.

без считывания информации с ДНК в ходе вычисления — по-

добное считывание при сегодняшних технологиях, по-видимо-

му, еще невозможно. Обсуждавшиеся выше о перац ии (слить,

разделить, включить, очистить) могут быть исполнены ро-

ботом, см. [291].

В [6] представлено самое эффектное из возможных прило-

жений стикерной модели — атака на криптосистему DES (Data

Encryption Standard, подробное описание этой криптосистемы

можно найти в [308]). Анализ, проведенный в [6], показывает,

что такую атаку можно осуществить с помощью ДНК-вычис-

лений, выполняемых роботом настольных размеров. Для вы-

числений потребуется приблизительно один грамм ДНК. Весь-

ма важно то, что шансы на успех достаточно велики даже в

том случае, когда при вычислениях допускается большое чис-

ло ошибок. Благодаря этому обстоятельству применение ДНК-

вычислений в задачах криптоанализа представляется особен-

но перспективным. В таких задачах никогда не приходится

рассчитывать на стопроцентный успех, но криптоаналитиче-

ская атака с использованием ДНК-вычисл ени й может удаться

с приемлемой вероятностью, даже если отдельные операции

над ДНК выполняются с ошибками.

Криптосистема DES преобразует 64-битные блоки текста

в 64-битные блоки криптотекста. Шифрование происходит с

помощью 56-битного ключа, который используется и для де-

шифрования. (DES — классическая симметричная криптоси-

стема с закрытым ключом в противоположность распростра-

ненным сейчас односторонним криптосистемам и криптосисте-

мам с открытым ключом.) Рассмотрим криптоаналитическ ую

атаку «известный текст» [308]. Такая атака означает, что крип-

тоаналитику известны несколько пар, состоящих из текста и

соответствующего кр ип тотекста, и на основе этой информации

криптоаналитик должен за разумное время определить ключ.

Высказывались предположения, что в случае DES это может

2.2. Решение задачи о выполнимости и взлом DES 83

быть проделано с помощью специализиров анных электронных

устройств или суперкомпьютера, использующего массирован-

ный параллелизм, однако пока что успеха добиться не уда-

лось

. Возможно, что подход, основанный на стикерной моде-

ли, будет более успешным, хотя в конечном счете только лабо-

раторные эксперименты решат, насколько он реал изуем.

Очевидным подходом к данной задаче является исчерпыва-

ющий перебор всех 2

ключей. (Свидетельством надежности

криптосистемы DES служит то, что до сих пор не известен ни-

какой существенно лучший подход.) Именно этот основанный

на «грубой силе» путь вполне годится для ДНК-вычислений.

Опишем криптоаналитическую атаку, предложенную в [6].

Используется стикерная модель; исходная пробирка является

(579,56)-библиотекой. Подцепочками запоминающих комплек-

сов служат олигонуклеотиды длины 20. Таким образом, длина

запоминающей цепочки составляет 11580 нуклеотидов. Такая

длина еще допустима, хотя для ол игонук леоти дов с длиной бо-

лее 15000 оснований есть опасность разрыва при переливании

и перемешивании содержимого пробирок.

В запоминающих комплексах обла сть из 56 подцепочек

отводится для хранения 56-битного ключа. В другой области

из 64 подцепочек после вычислений будет записан соответств у-

ющий криптотекст. Оставшиеся 459 подцепочек нужны для

хранения промежуточных резул ьтатов по ходу вычислений.

Известная пара из текста и криптотекста не записывается

в запоминающих комплексах и всегда остается неизменной.

Каждый ключ применяется к данному тексту, а получающийся

криптотекст сравнивается с известным криптотекстом. Таким

образом, вся процедура состоит из следующих трех шагов.

1. Построить исходную (579,56)-библиотеку, представляющую

все 2

ключей.

Примечание авторов к русскому переводу. Криптоанализ развивает-

ся очень быстро, и ситуация несколько изменилась с тех пор, как бы-

ли написаны эти строки. Исходная версия криптосистемы DES оказалась

ненадежной, и сейчас используются различные ее модификации, см. [173].

Однако и к ним в равной степени приложимы изложенные здесь идеи о

возможном использовании ДНК-вычислений в криптоанализе.

84 2. Начала молекулярных вычислений

2. Для каждого запоминающего комплекса выч исли ть крип-

тотекст, полученный шифрованием данно го т екста с клю-

чом, представленным этим запоминающим комплексом.

3. Выбрать запоминающий комплекс, для которого крипто-

текст совпадает с известным криптотекстом, и прочитать

его ключ.

Основная ча сть работы приходится на шаг (2). «Стикер-

ную машину», исполняющую алгоритм, можно мыслить себе

как виде параллельный роботизированный комплекс. В его со-

став входят стеллаж с пробирками (для данных, для стикеров

и для выполнения операц ий), роботы (манипуляторы, насосы,

нагреватели и охладители), а также микропроцессор, управля-

ющий роботами. Роботы предназначены для выполнения че-

тырех о перац ий, обсуждавшихся выше в связи со стикерной

моделью: слить, разделить, включить и очистить. При этом

роботы д олж ны осуществлять указанные операции параллель-

но над 64 пробирками. А именно, роботы могут слить ДНК

из 64 пробирок с данными в одну. Они одновременно могут раз-

делить 32 пробирок с ДНК на две пробирки каждую, исполь-

зуя 32 вспомогательные пробирки. Роботы могут включить i-

ю подцепочку во всех зап омина ющих комплексах в 64 пробир-

ках. Для этого они используют пробирку со стикерами для i-й

подцепочки и вспомогательную пробирку. Аналогично, роботы

могут очистить определенные подцепочки. Дальнейшие дета-

ли относительно реализации операций и алгоритм для шага (2)

читатель может найти в [6]. Мы заканчиваем этот раздел объ-

яснением того, как созд ается исходная библиотека на шаге (1).

Как можно создать все 2

возможных ключей? Применяемая

здесь техника представляет интерес для ДНК-вычислений во-

обще.

В начале берут приблизительно 2

одинаковых запомина-

ющих цепочек нуж ной длины, которые делят поровну на две

пробирки N

и N

. В пробирку N

добавляют большое коли-

чество каждого из 56 стикеров с тем, чтобы в результате реак-

ции сшивки включились все 56 подцепочек. Неиспользованные

стикеры вымывают из N

, после чего N

и N

сливают в одну

2.3. Переосмысление парадигмы вычислений 85

пробирку N . Наконец, пробирку N подогревают и остужают с

тем, чтобы стикеры сперва отклеились, а потом вновь прикле-

ились случайным образом. После такого про цесса образуют-

ся запоминающие комплексы, представляющие примерно 63%

ключей. Если же начать с утроенного количества ДНК, то доля

представленных ключей увеличится до 95%.

2.3 Переосмысление парадигмы вычислений

Приведет ли полномасштабная реализация идеи молекулярно-

го компьютера к полной замене или к значительному изме-

нению парадигмы вычислений? Именно эта тема обсуждается

в данном разделе. Мы используем здесь ставший в последнее

время весьма употребительным термин «паради гма» в значе-

нии «совокупность убеждений и мнений, принятых некоторым

научным сообществом». При обсуждении «парадигмы вычис-

лений» мы естественно считаем, что соответствующее научное

сообщество состоит из специалистов в области компьютерных

наук в самом широком смысле этого словосочетания.

Не п одлежит сомнению тот факт, что на протяжении уже

примерно полувека воплощением парадигмы вычислений яв-

ляется машина Тьюринга. Обратимся к основополагающей

статье Тьюринга [323] и посмотрим, какими аргументами он

обосновывает, что под его определени е «вычислимых» чисел

действительно подпадают все числа, которые могут считаться

вычислимыми с точки зрения здравого смысла. В современной

терминологии, это — аргументы в защиту тезиса Черч а–

Тьюринга, т. е. аргументы, объясняющие, почему машина

Тьюринга действительно вычисляет все вычислимое.

В [323] Тьюринг использует аргументы трех типов:

(1) Прямое обращени е к интуиц ии.

(2) Доказательство эквивалентности двух моделей.

(3) Предъявление обширн ых классов вычислимых чисел и де-

монстрация устойчивости вычислимости относительно раз-

личных операций.

86 2. Начала молекулярных вычислений

Аргументы типа (2) и (3) не имеют прямого от ношени я к на-

шей теме, а вот напомнить, что Тьюринг говорит по поводу (1),

важно, поскольку мы хотим противопоставить его представле-

ние о компьютере как о прилежном клерке идее компьютера

как множества цепочек ДНК. Послед ние никоим образом не

превосходят прилежного клерка в интеллектуальности — ско-

рее, дело обстоит как раз н аобор от. Однако их массирован ный,

теоретически не ограниченный параллелелизм меняет парадиг-

му, по крайней мере, в некоторых отношениях.

Тьюринг открывает аргумент (1) следующим образом.

,,Вычисления обычно выполняют, записывая некие символы

на бумаге. Мы можем предположить, что эта бумага поделена

на клетки, как в школьной тетради. В элементарной ариф-

метике ин огда используют двухмерность бумаги, но такое

использование всегда устранимо, и, я думаю, можно согла-

ситься с тем, что двухмерность бумаги несущественна для

вычислений. Итак, я предполагаю, что вычисление выпол-

няется на одномерной бумаге, т. е. на ленте, разделенной на

квадраты. Я буду также предполагать, что число символов,

которые могут быть напечатаны на ленте, конечно. Если бы

мы допустили бесконечность числа символов, то столкнулись

бы с символами, произвольно мало отличающимися друг от

друга. Эффект от ограничения на количество символов не

слишком серьезен: всегда можно использовать последователь-

ности символов вместо одиночных символов. . . . Поведение

вычислителя в каждый момент времени определяется симво-

лами, которые он обозревает, и его «состоянием ума» в этот

момент. Мы можем предполагать, что имеется ограничение на

количество символов или клеток, которые вычислитель может

обозревать за один момент времени. Если он хочет увидеть

больше символов, он должен будет осуществить ряд последо-

вательных наблюдений. Мы будем также предполагать, что и

число состояний ума, которые следует принимать во внимание,

конечно. Причина этого — та же, что и в случае с числом сим-

волов. Если мы допустим бесконечность числа состояний ума,

то некоторые из них будут «сколь угодно близки» и могут быть

2.3. Переосмысление парадигмы вычислений 87

перепутаны. Опять-таки, это ограничение не из тех, что серьез-

но влияют на п роц есс вычисления, поскольку использования

более сложных состояний ума можно избежать, записывая

больше символов на ленте. Представим опер аци и, выполня-

емые вычислителем, разделенными на «простые операции»,

которые элементарны настолько, что нелегко представить их

еще более разделенными. Каждая такая операция состоит

в некотором изменении физической системы, состоящей из

вычислителя и его ленты. Мы знаем состояние этой системы,

если мы знаем последовательность символов на ленте, знаем,

какие из них (и в каком порядке) обозреваются вычи слител ем,

и знаем состояние ума вычислителя.”

Анализ продолжается в том же духе. Не будет суще-

ственным ограничением, если предположить, что изменяются

только наблюдаемые клетки, а пр остая операция переписы-

вает не более одного символа. Так как новые наблюдаемые

клетки должны немедленно распознаваться вычислителем, их

расстояние до клеток, наблюдавшихся на предыдущем шаге,

не должно п ревышать некоторую фиксированную величину.

Применяя требование элементарности каждой индивидуаль-

ной операции, приводящее к необходимости заменять более

сложные операции последовательностью простых, можно за-

ключить, что общий вид индивидуальной операции — это

либо изменение набл юдаемого символа вкупе с возможным

изменением состояния ума, либо переход к наблюдению другой

клетки опять же вместе с возможным изменением состояния

ума. Таким образом, этот интуитивный анализ подводит к

стандартному описанию машины Тьюринга, которое будет

строго обсуждаться в главе 3.

Действия Тьюрингова вычислителя, прилежного клерка,

существенным образом последовательны. Он

работает шаг за

шагом, всегда имея дело лишь с некоторой частью потенци-

ально огромного набора данных. Ничего не происходит парал-

К слову отметим, что во времена Тьюринга в математической литера-

туре не было никаких переживаний по поводу употребления местоимений

«он» и «она». Тьюринг всегда говорит о своем клерке «он».

88 2. Начала молекулярных вычислений

лельно. Конечно, Тьюринг мог бы представить себе и команду

клерков, работающих одновременно, но тогда, очевидно, его

идея состояла бы в том, чтобы воспроизвести их действия с

помощью одного клерка, последовательно выполняющего все

индивидуальные задания. При этом во зросло бы (и, возможно,

чрезвычайно) время, необходимое для вычисления, но все рас-

смотрения, связанные со сложностью вычислений, не имеют

отношения к Тьюрингову клерку. Такие понятия, как «доступ-

ность» или «реализуемость», не говоря уже о «практической

осуществимости», Тьюринг не обсуждает.

То, что сказано о команде клерков, применимо также и к

наборам цепочек ДНК. Мы всегда можем тем или иным спосо-

бом имитировать массированный параллелизм молекул ДНК,

производя последовательно все действия, которые ДНК вы-

полняет параллельно. Поэтому ясно, что ДНК-компьютеры не

смогут опровергнуть тезис Черча–Тьюринга. Что бы не вычис-

лил ДНК-компьютер, мы можем призвать Тьюрингова кл ерка

и поручить ему произвести то же вычисление. Понятие вычис-

лимости или, в терминологии Тьюринга, множество вычисли-

мых чисел, не изменяется при вычислениях с помощью ДНК.

Парадигма вычислений, связанная с апостериорным понятием

вычислимости, представляется весьма устойчивой относитель-

но различных вычислительных моделей.

Ситуация меняется, когда пар адигма вычислений рассмат-

ривается в априорном смысле и, в частности, когда учитывает-

ся феномен сложности. Мы сталкиваемся с некоторой пробле-

мой и априори оценива ем свои возможности решить ее. Здесь

мы можем придти к разным заключениям в зависимости от

того, что имеется в нашем распоряжении — клерк Тьюрин-

га или пробирка с цепочками ДНК. В случае успеха ДНК-

компьютеров парадигма вычислений, рассматриваемая в таком

смысле, несомненно изменится. Это отражается и в теоретиче-

ских изысканиях, касающихся классов сложности. Среди ран-

них примеров — генетические м ашины Тью ринга, введенные

в [275]. В этой модели класс задач, решаемых за полиномиаль-

ное время (и в силу этого состоящий из вычислительно доступ-

2.3. Переосмысление парадигмы вычислений 89

ных задач), совпадает с классом PSPACE (который включает

в себя класс NP и вместе с ним очень много задач, традицион-

но считающихся вычислительно неприступными). Ниже будут

приведены и другие примеры.

Во второй части этой книги мы задаемся вопросом, воз-

можно ли построить универсальную вычислительную машину

из биологических макромолекулярных компонентов и выпол-

нять произвольные вычисления биологическими методами, и

в связи с этим исследуем различные математические модели.

Итог наших рассмотрений поразителен: оказывается, что (по

крайней мере, в теории) есть много различных подходов к по-

строению универсальных компьютеров, основанных на ДНК.

Мы постараемся сейчас объяснить, какая математическая пер-

вопричина стоит за этим обобщающим наблюдением.

Мы утверждаем, что именно комплементарность Уот-

сона–Крика обеспечивает универсальность в любой модели

ДНК-компьютера, обладающей достаточными возможностями

для управления вводом/выводом. Такое мнение впервые была

высказано и обосновано в [294]. Комплементарность Уотсона–

Крика тесно связана с языком перетасованных копий [84, 307].

В своем основном варианте такой язык использует две буквы 0

и 1, а также комплементарные и м буквы

0 и

1. (Формальное

определение языка перетасованных копий и математические

детали, обеспечивающие универсальность, приведены в разде-

ле 3.2, см., в частности, следствие 3.4 и теорему 3.18.) Его слова

вполне аналогичны молекулам ДНК, собранным из четырех

нуклеотидов, которые подразделяются на две комплементар-

ные пары: (А, Т) и (Ц, Г). Две буквы 0 и 1 используются для

кодирования информации, в то время как их комплементарные

версии

0 и

1 обеспечивают структуру, требуемую для описания

произвольных вычислений в терминах слов, взятых из языка

перетасованных копий. Именно в этом обстоятельстве заклю-

чена суть вычислительной универсальности; на него можно

также смотреть как на математическое объяснение того, что

число нуклеотидов в ДНК равно четырем. Трех нуклеотидов

было бы недостаточно для языка пер етасованных копий, в то

90 2. Начала молекулярных вычислений

же время как при пяти в слишком многи х ситуациях возника-

ла бы избыточность — ведь уже и сам язык перетасованных

копий до некоторой степени избыточен.

Как уже говорилось, мы займемся формальными деталями

ниже, в разделе 3.2. Тем не менее, мы хотим уже сейчас дать

некоторое представление о взаимосвязях между комплементар-

ностью Уотсона–Крика и языком перетасованных копий, по-

скольку именно они играют центральную роль в теории вы-

числений, основанных на ДНК. Мы обозначим язык перетасо-

ванных копий в его основном варианте (над четырехбуквенным

алфавитом {0, 1,

1}) через T S.

Рассмотрим слово w над алфавитом {0, 1}, т. е. строку, со-

стоящую из нулей и едини ц. Пусть w — комплементарная стро-

ка, построенная из

0 и

1. Например, если w = 00101, то w =

1. Мы обозначим через shuﬄe(w, w) множество всех слов,

получаемых с помощью перетасовки слов w и w, т. е. произ-

вольной вставки букв слова w между буквами слова w без изме-

нения порядка следования букв внутри этих словах. Например,

каждое из слов 0

11,

100101, 00

010

11 прина дле-

жит множеству shuﬄe(w, w), в то время как слово 0

там не содержится. По определению, язык T S состоит из всех

слов из shuﬄe(w, w), где w пробегает множество всех слов над

{0, 1}. Следующий простой прием позволяет определить, при-

надлежит ли данное слово x, построенное из четырех букв

0, 1,

1, языку T S. Сначала сотрем в x все буквы

0 и

1 и обо-

значим оставшееся слово через x

. Затем сотрем в x все бук-

вы 0 и 1, а также все черточки над остающимися буквами и

обозначим получившееся слово через x

. Тогда исходное слово

x принадлежит языку T S в том и только в том случае, когда

= x

. Читатель при желании может испытать этот пр ием на

примерах, приведенных выше.

Свяжем теперь «алфавит ДНК» и четырехбуквенный ал-

фавит {0, 1,

1} следующим образом:

А = 0, Г = 1, Т =

0, Ц =