Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

3.1. Основные понятия 111

RE CS CF LIN REG

Объединение Да Да Да Да Да

Пересечение Да Да Нет Нет Да

Дополнение Нет Да Нет Нет Да

Произведение Да Да Да Нет Да

∗-итерация Клини Да Да Да Нет Да

Пересечение с

регулярными языками Да Да Да Да Да

Подстановка Да Нет Да Нет Да

Нестирающая

подстановка Да Да Да Нет Да

Морфизмы Да Нет Да Да Да

Нестирающие морфизмы Да Да Да Да Да

Обратные морфизмы Да Да Да Да Да

Левое/правое частное Да Нет Нет Нет Да

Левое/правое частное

при делении Да Нет Да Да Да

на регулярные языки

Левая/правая

производная Да Да Да Да Да

Перетасовка Да Да Нет Нет Да

Зеркальное отражение Да Да Да Да Да

Таблица 3.1. Замкнутость семейств из иерархии Хомского.

Говорят, что ли нейн ая грамматика G = (N, T, S, P ) мини-

мальна, если N = {S} (т. е. в ней только один нетерминальный

символ).

Нормальные формы. Часто бывает полезным приведение

грамматик к какому-нибудь специальному виду без уменьше-

ния класса порождаемых ими языков. Известен ряд результа-

тов о существовании таких нормальных форм. Мы упомянем

только пять из них, которые будут полезны ниже.

Теорема 3.1 (форма Хомского). По каждой контекстно-сво-

бодной грамматике G эффективно строится эквивалентная

грамматика G

= (N, T, S, P ), все правила которой имеют вид

A → a или A → BC, где A, B, C ∈ N и a ∈ T .

112 3. Введение в теорию языков

Теорема 3.2 (сильная форма Хомского). По каждой кон-

текстно-свободной грамматике G эффективно строится

эквивалентная грамматика G

= (N, T, S, P ), все правила

которой имеют вид A → a или A → BC, где A, B, C ∈ N и

a ∈ T , причем выполняются следующие ограничения:

если A → BC — правило из P , то B 6= C;

если A → BC — правило из P , то для каждого правила A →

DE из P выполняется E 6= B и D 6= C.

Если нужно порождать и пустую строку, то в приведенных

выше теоремах следует допустить еще правило S → λ.

Теорема 3.3 (форма Куроды). По каждой грамматике G ти-

па 0 эффективно строится эквивалентная грамматика G

(N, T, S, P ), все правила которой имеют вид A → BC, A → a,

A → λ или AB → CD, где A, B, C, D ∈ N и a ∈ T .

Теорема 3.4 (форма Пенттонена). По каждой грамматике

G типа 0 эффективно строится эквивалентная грамматика

= (N, T, S, P ), все правила которой имеют вид A → x, где

x ∈ (N ∪ T )

∗

, |x| 6 2 или AB → AC, где A, B, C ∈ N.

Сходные результаты верны и для неукорачивающих грам-

матик; нужно лишь исключить правила вида A → λ, оставив

только правило S → λ, если нужно, чтобы пор ождаемый язык

содержал пустую строку.

Теорема 3.5 (формы Гефферта). (1) Каждый рекурсивно пе-

речислимый язык порождается грамматикой G = (N, T, S, P )

с N = {S, A, B, C}, правилами вида S → uSv, S → x, где

u, v, x ∈ (T ∪ {A, B, C})

∗

, и единственным не контекстно-сво-

бодного правилом ABC → λ.

(2) Каждый рекурсивно перечислимый язык порождается

грамматикой G = (N, T, S, P ) с N = {S, A, B, C, D}, прави-

лами вида S → uSv, S → x, где u, v, x ∈ (T ∪ {A, B, C})

∗

, и

ровно двумя не контекстно-свободными правилами AB → λ и

CD → λ.

Другими словами, каждый рекурсивно перечислимый язык

получается из некоторого минимального линейного языка при-

3.1. Основные понятия 113

менением либо одного правила сокращения ABC → λ, либо

пары правил сокращения AB → λ, CD → λ.

Необходимые условия. Для языка L ⊆ V

∗

мы определим

отношение эквивалентности ∼

на V

∗

, полагая x ∼

y тогда и

только тогда, когда (uxv ∈ L ⇔ uyv ∈ L) для в сех u, v ∈ V

∗

Легко проверить, что ∼

является конгруэнцией свободного

моноида V

∗

. Фактор V

∗

/ ∼

называется синтаксическим мо-

ноидом языка L.

Теорема 3.6 (Майхилл–Нероуд). Язык L ⊆ V

∗

регулярен то-

гда и только тогда, когда моноид V

∗

/ ∼

конечен.

Теорема 3.7 (о накачке для контекстн о-свободных языков).

Если L ∈ CF, L ⊆ V

∗

, то найдутся такие числа p, q ∈ N, что

каждую строку z ∈ L с |z| > p можно записать в виде z =

uvwxy, где u, v, w, x, y ∈ V

∗

, |vwx| 6 q, vx 6= λ и uv

y ∈ L

для всех i > 0.

Теорема 3.8 (о накачке для линейных языков). Если L ∈

LIN , L ⊆ V

∗

, то найдутся такие числа p, q ∈ N, что каждую

строку z ∈ L с |z| > p можно записать в виде z = uvwxy, где

u, v, w, x, y ∈ V

∗

, |uvxy| 6 q, vx 6= λ и uv

y ∈ L для всех

i > 0.

Теорема 3.9 (о накачке для регулярных языков). Если L ∈

REG, L ⊆ V

∗

, то найдутся такие числа p, q ∈ N, что каждую

строку z ∈ L с |z| > p можно записать в виде z = uvw, где

u, v, w ∈ V

∗

, |uv| 6 q, v 6= λ и uv

w ∈ L для всех i > 0.

Теорема 3.10 (Парих). Любой контекстно-свободный я зык

является полулинейным.

Следствие 3.1. (i) Каждый контекстно-свободный язык над

однобуквенным алфавитом регулярен.

(ii) Множество длин контекстно-свободного языка есть

объединение конечного числа арифметических прогрессий.

Условия теорем 3.7–3.10 необходимы, но не достаточны для

того, чтобы язык лежал в соответствующем семействе.

114 3. Введение в теорию языков

Пользуясь этими необходимыми условиями, можно дока-

зать следующие включения:

= {a

| n > 1} ∈ LIN − REG,

= L

∈ CF − LIN,

= {a

| n > 1} ∈ CS − CF,

= {xcx | x ∈ {a, b}

∗

} ∈ CS − CF,

= {a

| n > 1} ∈ CS − CF,

= {a

| n, m > 1} ∈ CS − CF,

= {a

| n > 1, 1 6 m 6 2

} ∈ CS − CF,

= {a

| 1 6 n 6 m 6 p} ∈ CS − CF,

= {x ∈ {a, b}

∗

| |x|

= |x|

} ∈ CF − LIN,

= {x ∈ {a, b, c}

∗

| |x|

= |x|

} ∈ CS − CF.

Язык Дика D

над T

= {a

, a

, . . . , a

, a

}, n > 1, — это

контекстно-свободный язык, порожденный грамматикой

G = ({S}, T

, S, {S → λ, S → SS} ∪ {S → a

| 1 6 i 6 n}, S).

Для наглядности пары (a

, a

), 1 6 i 6 n, можно интерпретиро-

вать как левые и правые скобки различных видов. Тогда язык

состоит из всех строк правильно расставленных скобок.

Теорема 3.11 (Хомский–Шютценберже). Любой контекстно-

свободный язык L представим в виде L = h(D

∩ R), где h —

морфизм, D

— язык Дика, а R — регулярный язык .

Системы Линденмайера. Как и механизмы порождения

строк, вводимые в последующих разделах, системы Линден-

майера или L-системы, которые мы время от времени будем

упоминать, возникли из биологических соображений. Здесь

мы приведем основные определения.

В общих чертах, 0L-система (система Линденмайера с ну-

левым взаимодействием) — это контекстно-свободная чистая

грамматика с параллельным выводом: G = (V, w, P ), где V —

алфавит, w ∈ V

∗

(аксиома), и P — конечное множество пра-

вил вида a → v, где a ∈ V , v ∈ V

∗

, причем для каждой

буквы a ∈ V в P найдется по крайней мере одно правило

3.1. Основные понятия 115

a → v (мы будем говорить, что P полно). Для w

, w

∈ V

∗

мы пишем w

=⇒ w

, если w

= a

· · · a

, w

= v

· · · v

→ v

∈ P для каждого i = 1, . . . , n. Язык, порожденный

G — это L(G) = {x ∈ V

∗

| w =⇒

∗

x}.

Если v 6= λ в каждом правиле a → v ∈ P , то будем гово-

рить, что G — размножающая (нестирающая) система; если

для каждого a ∈ V существует ровно одно правило a → v

в P , то говорят, что G — детерминированная система. Если

выделено подмножество T в V и язык L(G) определен как

L(G) = {x ∈ T

∗

| w =⇒

∗

x}, то G называют расширенной

системой. Семейство языков, порожденных 0L-системами, обо-

значают через 0L; если речь идет о ра змножающей, детерми-

нированной или расширенной 0L-системе, то перед 0L д обав-

ляется буква P, D или соответственно Е.

Табличной 0L-системой, сокращенно T0L, называется такая

система G = (V, w, P

, . . . , P

), что каждая тройка (V, w, P

1 6 i 6 n, является 0L-системой, при этом каждое множество

правил P

называется таблицей. Язык, порожденный G, опре-

деляется следующим образом:

L(G) = {x ∈ V

∗

| w =⇒

=⇒

. . . =⇒

= x,

m > 0, 1 6 j

6 n, 1 6 i 6 m}.

(Каждый шаг вывода выполняется с помощью пр авил ровно

одной таблицы.)

T0L-система детерминирована, если детерминирована каж-

дая из ее таблиц. Аналогичным образом определяются размно-

жающие и расширенные T0L-системы.

Семейство языков, порожденное T0L системами, обозначим

через T 0L; через ET 0L, EDT 0L и т. е. обозначим семейства

языков, получаемые по аналогии с E0L, ED0L и т. д.

Семейство D0L несравнимо с FIN, REG, LIN, CF, в то вр е-

мя как E0L строго содержи т семейство CF ; ET 0L является

наибольшим семейством языков Линденмайера с нулевым вза-

имодействием, оно строго содержится в CS и является полным

AFL. Идея нулевого взаимодействия соответствует контекст-

116 3. Введение в теорию языков

ной независимости: каждая буква развивается независимо от

своих соседей.

Интересной чертой D0L-системы G = (V, w, P ) является

то, что она порождает свой язык в виде последовател ьности,

L(G) = {w = w

, w

, . . . } такой, что w

=⇒ w

=⇒

. . . . Таким образом, для G можно определить функцию роста

growth

: N −→ N с помощью равенства

growth

(n) = |w

|, n > 0.

Дескриптивная сложность. Один и тот же язык может

быть порожден многими (и часто даже бесконечно многи-

ми) грамматиками. Естественно искать среди них наиболее

простые, для чего и нужны меры сложности грамматик.

Для к ласса грамматик X мера дескриптивной (или син-

таксической) сложности есть отображение K : X −→ N, кото-

рое равенством K(L) = min{K(G) | L = L(G), G ∈ X} распро-

страняется на языки, порождаемые грамматиками из X. Если

нужно указать на используемый класс грамматик, мы будем

писать K

(L).

Следующие три меры являются основными для контекстно-

свободных языков. Для контекстно-свободной грамматики G =

(N, T, S, P ) определим

Var(G) = card(N),

Prod(G) = card(P ),

Symb(G) =

r∈P

Symb(r), где Symb(r : A → x) = |x| + 2.

Мера сложности K называется нетривиальной, если для

каждого n найдется такая грамматика G

, что K



L(G

)



> n;

говорят, что мера K связная, если существует такое n

, что

для каждого n > n

найдется грамматика G

со свойством



L(G

)



= n.

Все три меры Va r, Prod, Symb связные (даже по отношению

к семейству регулярных языков). В общем случае две меры

синтаксической сложности не могут быть одновременно улуч-

3.1. Основные понятия 117

шены: чаще всего грамматика, оказавшаяся проще по отноше-

нию к одной мере, будет сложнее с точки зрения другой меры.

Важной мерой сложности является индекс. Пусть G =

(N, T, S, P ) — грамматика любого типа. Для вывода

D : S = w

=⇒ w

=⇒ . . . =⇒ w

= x ∈ T

∗

положим

Ind(D) = max{|w

| 0 6 i 6 n}.

Для каждого x ∈ L(G) определим

Ind(x, G) = min{Ind(D) | D : S =⇒

∗

x ∈ G}.

Затем введем

Ind(G) = sup{Ind(x, G) | x ∈ L(G)}.

И, наконец, для языка L положим

Ind(L) = min{Ind(G) | L = L(G)}.

Ясно, что Ind(L) = 1 для каждого линейного языка L. Из-

вестно, что Ind(D

) = ∞, n > 1, и что Ind — связная мера по

отношению к семейству контекстно-свободных языков. Более

того, семейство

fin

= {L ∈ CF | Ind

(L) < ∞}

является полным AFL.

Автоматы и преобразователи. Автоматы — это устройст-

ва, определяющие языки способом, противоположным тому,

каким их определяют грамматики. Автомат получает строки

над данным алф авито м и анализирует (говорят также распо-

знает) их, сообщая, лежит ли та или иная строка в интересу-

ющем нас языке.

Пять основных семейств языков в иерархии Хомского,

REG, LIN, CF, CS, RE, могут быть охарактеризованы и в тер-

минах распознающих автоматов. Соответствующие автоматы

суть конечные автоматы, однопроходные магазинные автома-

ты, магазинные автоматы, линейно ограниченные автоматы и

машины Тьюринга. Мы опишем здесь только основные вариан-

118 3. Введение в теорию языков

ты этих устройств; описания многих других их разновидностей

см. в [145, 223, 302, 305].

Конечный (недетермини рова нный ) автомат — это пятерка

M = (K, V, s

, F, δ),

где K и V — непересекающиеся алфавиты, s

∈ K, F ⊆ K,

δ : K × V −→ P(K). Здесь K — множество состояний, V —

алфавит автомата, s

— начальное состояние, F — множество

заключительных состояний, δ — функция переходов. Е сли

card



δ(s, a)



6 1 для всех s ∈ K, a ∈ V , то говорят, что авто-

мат детерминированный. Отношение ` на множестве K × V

∗

определяется так: для s, s

∈ K, a ∈ V , x ∈ V

∗

мы пишем

(s, ax) ` (s

, x), если s

∈ δ(s, a), и, кроме того, (s, λ) ` (s, λ).

Если `

∗

— рефлексивное и транзитивное замыкание отноше-

ния `, то язык, распознаваемый автоматом M, есть

L(M) = {x ∈ V

∗

| (s

, x) `

∗

(s, λ), s ∈ F }.

Известно, ч то детерминированные и недетерминированные

конечные автоматы характеризуют одно и то же семейство

языков, а именно REG. Выразительная сила конечных автома-

тов не увеличится, если допустить λ-переходы, т. е. определять

δ на множестве K × (V ∪ {λ}) (тогда автомат может изменить

состояние без чтения символа), ил и если допустить, что авто-

мат может сканировать входную строку в двух направлениях,

двигаясь вдоль нее вправо и влево, но не меняя ее символов.

Родственно понятию конечного автомата важное понятие

последовательного преобразователя ил и ОПМ (от «Обобщен-

ная Последовательная Машина» ). Такое устройство есть ше-

стерка g = (K, V

, V

, s

, F, δ), где K, s

, F те же, что и в опре-

делении конечного автомата, V

, V

— входной и выходной ал-

фавиты, а δ : K × V

−→ P

∗

× K). Если δ(s, a) ⊆ V

× K

для всех s ∈ K, a ∈ V

, то ОПМ g называется λ-свободной. Ес-

ли card



δ(s, a)



6 1 для всех s ∈ K, a ∈ V

, то говорят, что

g детерминирована. Для s, s

∈ K, a ∈ V

, y ∈ V

∗

, x, z ∈ V

∗

полагаем (x, s, ay) ` (xz, s

, y), если (z, s

) ∈ δ(s, a). Тогда для

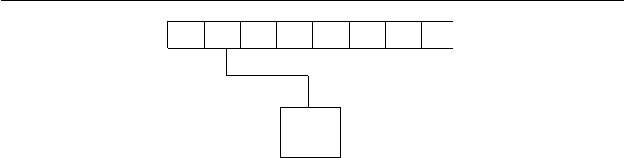
3.1. Основные понятия 119

Рис. 3.1. Конечный автомат.

w ∈ V

∗

определим

g(w) = {z ∈ V

∗

| (λ, s

, w) `

∗

(z, s, λ), s ∈ F }.

Отображение g можно естественным образом распространить

на языки в алфавите V

На ОПМ можно смотреть как на конечный автомат с выхо-

дом. Легко видеть, что каждое замкнутое относительно ОПМ-

отображений семейство языков будет замкнуто относительно

конечных подстановок (а, значит, и относительно морфизмов)

и операций Sub, Pref, Suf.

Конечный автомат можно мыслить себе как устройство,

изображенное на рис. 3.1, где показаны входная лента, в клет-

ках которой записаны символы входного алфави та, ч итающая

головка, просматривающая ленту слева направо, и память,

которая способна хран ить состояние из некоторого конечного

множества. Аналогично, ОПМ — это устройство, изображенное

на рис. 3.2, где есть еще выходная лента, на которой пишущая

головка может записывать строку, получающуюся в результате

переработки входной строки.

Иногда бывает пол езно представлять функцию перехода ко-

нечного автомата и ОПМ как множество переписывающих пра-

вил. В таком случае мы пишем sa → as

вместо s

∈ δ(s, a) в

случае конечных автоматов и sa → zs

вместо (z, s

) ∈ δ(s, a)

в случае ОПМ. Тогда отношения `, `

∗

в точности совп ада ют

с =⇒, =⇒

∗

в соответствующей переписывающей системе. Для

ОПМ g и языка L ∈ V

∗

имеем

g(L) = {z ∈ V

∗

| s

w =⇒

∗

zs, w ∈ L, s ∈ F }.

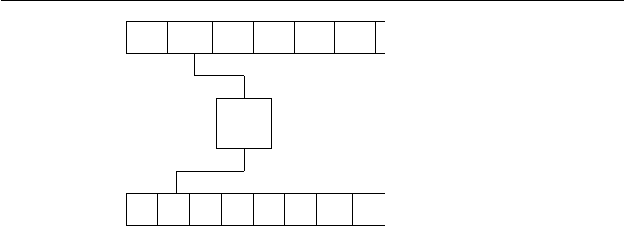
120 3. Введение в теорию языков

Рис. 3.2. Последовательный преобразователь.

В частном случае конечного автомата имеем

L(M) = {x ∈ V

∗

| s

x =⇒

∗

xs, s ∈ F }.

Магазинным автоматом называется семерка

M = (K, V, U, s

, Z

, F, δ),

где K, V , U — алфавиты (состояний, входных символ ов и мага-

зинных символов), K не пересекается ни с V , ни с U, s

∈ K —

начальное состояние, Z

∈ U — символ, отмечающий дно ма-

газина, F ⊆ K — множество заключительных состояний, а

δ : K × (V ∪ {λ}) × U −→ P

(K × U

∗

) — функция переходов.

Конфигурация магазинного автомата M — это тройка

(s, w, z), где s ∈ K — текущее состояние, w ∈ V

∗

— еще не

просмотренная часть входной строки, z ∈ U

∗

— содержимое

магазина. Для пары конфигураций (s, w , z), (s

, w

, z

) опреде-

лим отношение (s, w, z) ` (s

, w

, z

) следующей совокупностью

условий:

w = aw

, где a ∈ V ∪ {λ},

z = αz

, z

= z

, где α ∈ U, z

, z

∈ U

∗

, (s

, z

) ∈ δ(s, a, α).

При этом говорят, что автомат, находясь в состоянии s, считы-

вает крайний левый символ a строки w и переходит в состояние

, зависящее как от a и s, так и от верхнего символа α в мага-

зине, который одновременно заменяется на слово z

. Отметим,

что символ a может быть и пустым. В случае, когда z

= λ,

говорят, что α выталкивается из магазина.