Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений
Подождите немного. Документ загружается.


3.2. Характеризации рекурсивно перечислимых языков 141
разователя исходя из единственного языка T S
{0,1}
. Можно
показать, что этот преобразователь может быть выбран детер-
минированным.
Любопытно, что приведенный выше результат спр аведл ив
и для «зеркального» варианта языка перетасованных копий.
Для данного алфавита V язык
RT S
V
=
[
x∈V
∗
x t⊥ mi(¯x)
называется языком перетасованных отражений над V .
Теорема 3.18. Для любого языка L ∈ RE существует такая
детерминированная ОПМ g
L
, что L = g
L
(RT S
{0,1}
).
Доказательство. Поскольку множество детерминированных
ОПМ замкнуто относительно композиции, достаточно найти
такую детерминированную ОПМ g, что g(RT S
{0,1}
) = T S
{0,1}
.
Искомая ОПМ будет определена для строк из
D = {01, 10,
¯
0
¯
1,
¯
1
¯
0}
∗
00
¯
0
¯
0{01
¯
0
¯
1, 10
¯
1
¯
0}
∗
.
Каждую строку w ∈ D можно представить как w = h(u)00
¯
0
¯
0v,
где u, v ∈ {0, 1,
¯
0,
¯
1}
∗
, а h — морфизм, определяемый правила-
ми h(0) = 01, h(1) = 10, h(
¯
0) =
¯
0
¯
1, h(
¯
1) =
¯
1
¯
0. Тогда зададим
отображение g правилом g(w) = u. Легко видеть, что g — де-
терминированное ОПМ-отображение. Остается показать, что
g(RT S
{0,1}
) = T S
{0,1}
.
Рассмотрим w = h(u)00
¯
0
¯
0v ∈ RT S
{0,1}
∩ D. Из равенства
pr
{
¯
0,
¯
1}
(w) = mi(pr
{0,1}
(w))
и наличия у w «маркера» 00
¯
0
¯
0 посередине следует, что
pr
{
¯
0,
¯
1}
h(u)
= mi(
pr
{0,1}
(v)) и pr
{
¯
0,
¯
1}
(v) = mi(pr
{0,1}
(h(u))).
Ввиду того, что v ∈ {01
¯
0
¯
1, 10
¯
1
¯
0}
∗
, имеем pr
{
¯
0,
¯
1}
(v) = pr
{0,1}
(v),
откуда вытекает, что pr
{
¯
0,
¯
1}
h(u)
= pr
{0,1}
h(u)
. Значит,
h
pr
{
¯
0,
¯
1}
(u)
= h(pr
{0,1}
(u)), и поскольку морфизм h инъекти-
вен, pr
{
¯
0,
¯
1}
(u) = pr
{0,1}
(u), т. е. g(w) = u ∈ T S
{0,1}
. Тем самым,
мы показали, что g(RT S
{0,1}
) ⊆ T S
{0,1}
.

142 3. Введение в теорию языков
Обратно, пусть слово u ∈ {0, 1,
¯
0,
¯
1}
∗
обладает свойством
pr
{
¯
0,
¯
1}
(u) = pr
{0,1}
(u). Рассмотрим строку w = h(u)00
¯
0
¯
0v, в
которой v — единственный элемент из {01
¯
0
¯
1, 10
¯
1
¯
0}
∗
такой,
что pr
{0,1}
(v) = mi
pr
{0,1}
h(u)
. Тогда w ∈ D ∩ RT S
{0,1}
и
g(w) = u, что и завершает доказательство.
Результаты, аналогичные следствию 3.4 и теореме 3.18, име-
ют место и для других вариантов языка перетасованных копий.
Рассмотрим кодирование c : {0, 1}
∗
−→ {
¯
0, 1}
∗
по правилу
c(0) =
¯
0 и c(1) = 1. Язык ST S
{0,1}
перетасованных полукопий
над {0, 1} определяется формулой
ST S
{0,1}
=
[
x∈{0,1}
∗
x t⊥ c(x)
.
Теорема 3.19. Для любого рекурсивно перечислимого языка
L существует такая ОПМ g
L
, что L = g
L
(ST S
{0,1}
).
Доказательство. С учетом следствия 3.4, достаточно подо-
брать такую ОПМ g, что T S
{0,1}
= g(ST S
{0,1}
). Определим
морфизм h : {0, 1,
¯
0,
¯
1}
∗
−→ {0, 1,
¯
0}
∗
по правилу
h(0) = 00, h(1) = 01, h(
¯
0) =
¯
0
¯
0, h(
¯
1) =
¯
01
и введем регулярный язык R = {00, 01,
¯
0
¯
0,
¯
01}
∗
. Убедимся, что
тогда
T S
{0,1}
= h
−1
(ST S
{0,1}
∩ R).
Рассмотрим строку y ∈ T S
{0,1}
. Тогда y ∈ x t⊥ ¯x для неко-
торой строки x ∈ {0, 1}
∗
. Ясно, что
h(y) ∈ h(x) t⊥ h(¯x) = h(x) t⊥ c
h(x)
.
Следовательно, h(y) ∈ ST S
{0,1}
. Очевидно, что h(y) ∈ R , зна-
чит, выполняется включение T S
{0,1}
⊆ h
−1
(ST S
{0,1}
∩ R).
Обратно, возьмем строку z ∈ ST S
{0,1}
∩ R и найдем h
−1
(z).
В силу инъективности h множество h
−1
(z) одноэлементно (оно
непусто для всех z ∈ R). По опред елени ю языка ST S
{0,1}
имеем
z ∈ x t⊥ c(x) для некоторой строки x ∈ {0, 1}
∗
. Так как z ∈ R,
имеем x ∈ {00, 01}
∗
, т. е. c(x) ∈ {
¯
0
¯
0,
¯
01}
∗
. Рассмотрим теперь
строки y = h
−1
(x) и ¯y. Имеем ¯y = h
−1
(x) = h
−1
c(x)
, откуда

3.3. Универсальные машины Тьюринга 143
h
−1
(z) ∈ h
−1
x t⊥ c(x)
= h
−1
(x) t⊥ h
−1
c(x)
=
= h
−1
(x) t⊥ h
−1
(x) ⊆ T S
{0,1}
.
Тем самым, доказано и включение h
−1
(ST S
{0,1}
∩ R) ⊆ T S
{0,1}
.
Осталось замети ть, что и пересечение с регулярным язы-
ком, и обратный морфизм могут быть одновременно вычисле-
ны с помощью подходящей ОПМ.
Можно п олучи ть и соответствующий аналог теоремы 3.18.
Язык RST S
{0,1}
перетасованных полуотражений над {0, 1}
определяется как
RST S
{0,1}
=
[
x∈{0,1}
∗
x t⊥ c
mi(x)
.
Следующий результат доказывается так же, как теорема 3.19:
Следствие 3. 5. Для л юбого рекурсивно перечислимого языка
L существует такая ОПМ g
L
, что L = g
L
(RST S
{0,1}
).
3.3 Универсальные машины Тьюринга и
грамматики типа 0
Компьютер — это программируемая машина, способная выпол-
нить любую загруженную в нее программу. Соответствующим
теоретическим по нятием служит универсальная машина Тью-
ринга, и вообще, машина, универсальная в данном классе ма-
шин.
Рассмотрим машину Тьюринга M = (K, V, T, B, s
0
, F, δ) с
входным алфавитом T . Как обсуждалось раньше, M начинает
работу со строки w, записанной на ее ленте, и в зависимости от
того, лежит ли w в L(M) или нет, либо достигает заключитель-
ного состояния (и останавливается), либо нет. Саму машину
Тьюринга также можно закодировать строкой символов в под-
ходящем алфавите. Обозначим такую строку через code(M).
Теперь представим себе машину Тьюринга M
u
, которая начи-
нает работу со строки, содержащей и w ∈ T
∗
, и code(M ) для
данной машины Тьюринга M , и останавливается в заключи-
тельном состоянии тогда и только тогда, когда w ∈ L(M).

144 3. Введение в теорию языков
В принципе, конструкция такой машины M
u
проста. От
M
u
требуется лишь моделировать работу произвольной маши-
ны Тьюринга, и ясно, как это можно делать: в соответствии с
отображением δ ищем пер еход, определяемый текущим состоя-
нием и текущим положением читающей/пишущей головки (эта
информация содержится в мгновенных описаниях конкретной
моделируемой машины); когда переход возможен нескольки-
ми способами, делаем копии текущего мгновенного описания
и разветвляем эволюцию машины; при появлении двух копий
одного и того же мгновенного описания стираем одну из них;
если хотя бы один из вариантов эволюции приводит к прини-
маемой конфигурации, то останавливаемся и считаем входную
строку принятой, а в противном случае продолжаем процесс.
Такая машина M
u
называется универсальной. Она может
моделировать любую наперед заданную машину Тьюринга при
условии, что код данной машины записан на л енте универсаль-
ной машины вместе со входной строкой.
Ясна аналогия с привычным нам компьютером: код маши-
ны Тьюринга — это программа, строки, которые нужно распо-
знать, — это исходные данные, а универсальная машина Тью-
ринга — это и есть собственно компьютер.
Мы хотим подчеркнуть важное различие между вычисли-
тельной полнотой и универсальностью. Класс C вычислитель-
ных устройств называется вычислительно полным, если вы-
числительная сила устройств из C такая же, как у машин Тью-
ринга (или эквивалентных им устройств другого типа). Это
означает, что по данной машине Тьюринга M можно найти эк-
вивалентное ей устройство из C. Таким образом, п олн ота есть
способность вычислить всё вычислимое (или, в грамматиче-
ских терминах, породить все рекурсивно перечислимые язы-
ки). Универсальность же является внутренним свойством клас-
са C и означает наличие в нем такого элемента, который может
моделировать любой другой элемент из C методом, описанным
выше применительно к машинам Тьюринга.
Разумеется, можно определить и относительную полноту,
имея в виду не весь класс машин Тьюринга, а некоторый

3.3. Универсальные машины Тьюринга 145
его подкласс. В этом смысле можно говорить, например, о
контекстно-свободной полноте (способн ости породить все кон-
текстно-свободные языки). Аналогично, можно искать и уни-
версальные элементы в классах вычислительных устройств,
полных относительно собственных подсемейств семейства
рекурсивно перечислимых языков. Однако для любой тео-
рии, цель которой — предложить общие модели вычислений,
важны полнота и универсальность по отношению ко всем
машинам Тьюринга, и именно в таком смысле эти понятия
будут рассматриваться в данной книге.
Идея универсальной машины была высказана самим Тью-
рингом, построившим и первый пример такой машины [323].
Сейчас в литературе имеется много примеров универсальных
машин Тьюринга, среди которых есть простые (или даже ми-
нимальные) с различных точек зрения. Ниже мы воспроизво-
дим некоторые такие примеры, в которых машина Тьюринга
рассматривается как устройство, вычисляющее отображения
(см. раздел 3.1). При данном подходе машина Тьюринга уни-
версальна, если она вычисляет универсальную частично рекур-
сивную функцию (по модулю упомянутого в разделе 3.1 «ин-
терфейса» кодирования-декодирования). По аналогии с этим
скажем, что машина M
1
моделирует машину M
2
, если най-
дутся такие отображения кодирования и декодирования
C : ID
M
2
−→ ID
M
1
, D : ID
M
1
−→ ID
M
2
,
что для каждого α ∈ ID
M
2
выполняется соотношение
D
F
M
1
C(α)
= F
M
2
(α).
Сложность машины Тьюринга можно измерять разными
параметрами: количеством состояний, количеством символов
ленты (вкл ючая пробел), количеством переходов (т. е. пяте-
рок (s, a, b, d, s
0
) таких, что (s
0
, b, d) ∈ δ(s, a)). Обозначим через
UTM(m, n) класс универсальных детерминированных машин
Тьюринга с m состояниями и n символами ленты (тогда число
переходов не может превосходить m · n − 1, поскольку должны
быть конфигурации, в которых машина останавливается).
146 3. Введение в теорию языков
B 1 a b
s
0
BLs
0
BLs
0
bRs
1
aLs
0
s
1
1Rs
1
BLs
0
bRs
1
1Rs
4
s
2
1Ls
3
1Rs
2
bRs
2
aRs
2
s
3
1Ls
6
1Ls
3
bLs
3
aLs
3
s
4
bLs
3
1Rs
4
bRs
4
aRs
4
s
5
BRs
4
BRs
5
aRs
5
BRs
0
s
6
BRs
2
– aLs
5
–
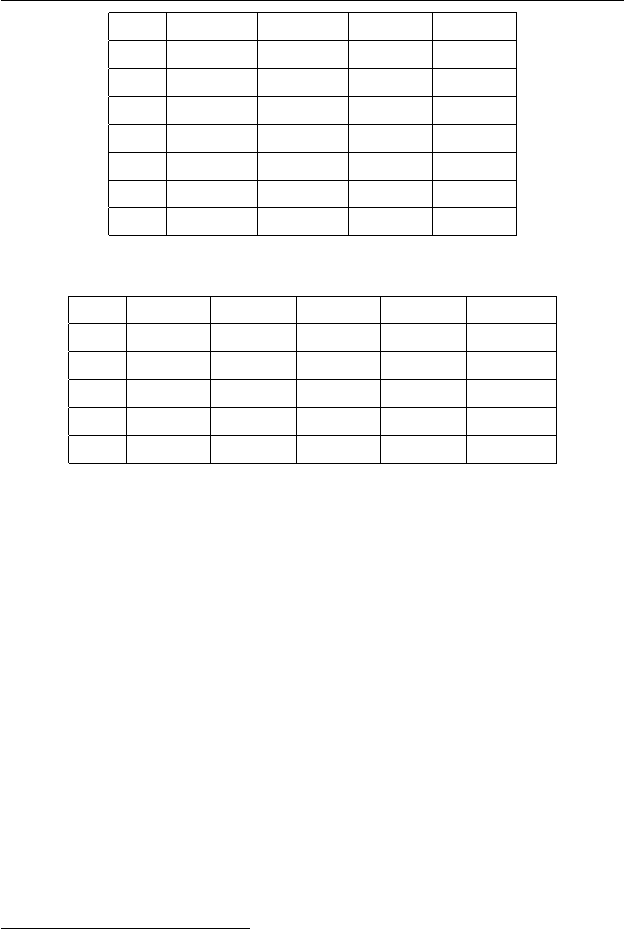
Таблица 3.2. Машина Тьюринга из UTM(7, 4).
B 0 1 a b
s
0
bRs
0
1Rs
0
0Ls
0
0Rs
1
BLs
0
s
1
0Ls
3
0Rs
1
0Rs
1
aRs
1
bRs
1
s
2
BRs
4
aLs
3
0Rs
2
aRs
2
bRs
2
s
3
bLs
2
1Ls
3
0Rs
1
aLs
3
bLs
3
s
4
– – 1Rs
4
1Rs
0
BRs
4
Таблица 3.3. Машина Тьюринга из UTM(5, 5).
Малые универсальные машины Тьюринга были построены
уже в [313] (машина с двумя состояниями) и в [223] (машина с
семью состояниями и четырьмя символами). Сводка результа-
тов в этой области дана в [284]:
Теорема 3.20. (i) Классы UT M(2, 3), UT M(3, 2) пусты.
(ii) Следующие классы не пусты: UT M(24, 2), U T M(10, 3),
UTM(7, 4), UT M(5, 5), UT M(4, 6), UT M(3, 10), UT M(2, 18).
Таким образом, проблема остается открытой для 51 класса
UTM(m, n).
1
Напомним три примера универсальных машин Тьюринга из
классов U T M(7, 4), UT M(5, 5), UT M(4, 6) [284] (см. табл. 3.2 –
3.4); последний из них имеет наименьшее количество перехо-
дов. Поскольку машины детерминированные, представим их в
виде таблиц: для каждой пятерки (s, a, b, d, s
0
), запишем bds
0
1
Примечание переводчика. Недавно построены машины в классах
UT M(19, 2) [19] и UT M (3, 9) [172], в силу чего число классов U T M (m, n)
с открытой проблемой пустоты сократилось до 45.
3.3. Универсальные машины Тьюринга 147
B 1 a b b
0
b
00
s
0
b
00
Ls
0
b
00
Ls
0
0Rs
3
b
0
Rs
0
bLs
0
0Rs
0
s
1
1Ls
1
BRs
1
bRs
1
b
0
Ls
2
b
00
Rs
1
b
0
Ls
1
s
2
aRs
0
1Rs
2
1Rs
0
b
00
Rs
3
bRs
2
–
s
3
aLs
1
0Rs
3
bRs
3
aLs
1
b
00
Rs
3
–
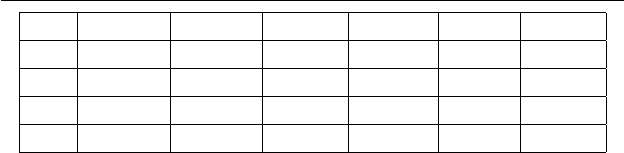
Таблица 3.4. Машина Тьюринга из UTM(4, 6).
на пересечении строки, помеченной s, и столбца, помеченно го
a. Состояния обозначены через s
0
, s
1
, . . . , s
m
, а символ пробела
через B. (Мы не приводим здесь отобра жения кодирования и
декодирования C, D; читатель может найти детали в [284].)
Видно, что число пер еходов у этих машин — соответственно
26, 23 и 22. Это лучшие из известных результатов (см. [284]).
Большинство конструкций, на которых основаны доказа-
тельства в следующих главах, отправляются от грамматик
Хомского типа 0. По данной машине Тьюринга M эффектив-
но строится такая грамматика G типа 0, что L(M) = L(G).
(Аналогично можно постр оить и такую грамматику G типа 0,
которая вычисляет, используя подходящие отображения ко-
дирования и декодирования, то же отображение F
M
, что и
M. Поэтому грамматику можно рассматривать не только как
механизм, порождающий язык, но и как устройство, вычис-
ляющее функцию.) Идея построения очень проста. Возьмем
машину Тьюринга M = (K, V, T, B, s
0
, F, δ) и постро им неогра-
ниченную грамматику Хо мского G, работающую так: начиная
со своей аксиомы, G недетерминировано порождает строку
w над алфа витом V , затем делает копию w (конечно, две
копии строки w разделяются подходящим маркером; маркеры
и д ругие вспомогательные символы вполне допустимы, потому
что их можно стереть, когда необходимость в них отпадет). На
одной из копий строки w грамматика G может моделировать
работу машины M, недетерминировано выбирая вычисление в
соответствии с функцией δ; если достигнуто заключительное
состояние, то эта копия сохраняется, а все остальное стирается.
Ради полноты изложения, приведем детали такой конструк-
ции. Рассмотрим детерминированную машину Тьюринга M =

148 3. Введение в теорию языков
(K, V, T, B, s
0
, F, δ) и построим грамматику G = (N, T, S, P ), в
которой N = {[a, b] | a ∈ T ∪ {λ}, b ∈ V } ∪ {S, X, Y } ∪ K, а P
содержит следующие правила вывода:
1) S → s
0
X ,
2) X → [a, a]X для a ∈ T,
3) X → Y,
4) Y → [λ, B]Y,
5) Y → λ,
6) s[a, α] → [a, β]s
0
для таких a ∈ T ∪ {λ}, s, s
0
∈ K, α, β ∈ V,
что δ(s, α) = (s
0
, β, R),
7) [b, γ]s[a, α] → s
0
[b, γ][a, β] для таких α, β, γ ∈ V,
a, b ∈ T ∪ {λ}, s, s
0
∈ K, что δ(s, α) = (s
0
, β, L),
8) [a, α]s → sas,
s[a, α] → sas,
s → λ для a ∈ T ∪ {λ}, α ∈ V, s ∈ F.
Легко убедиться, что L(G) = L(M).
Применяя эту конструкцию к универсальной машине Тью-
ринга M
u
, получим универсальную грамматику Хомского ти-
па 0. Эта грамматика универсальна в следующем смысле: по-
рождаемый ею язык состоит из строк вида w# code(M) та-
ких, что w ∈ L(M). (Язык {w# code(M) | w ∈ L(M)} можно
назвать универсальным, и любая грамматика, порождающая
этот язык, будет универсальной.) Однако нас интересует «бо-
лее гр амматическое» понятие универсальности, которое приво-
дит к следующему определению.
Тройка G = (N, T, P ), компоненты N, T, P которой име-
ют тот же смысл, что и в обычной грамматике Хомского, на-
зывается грамматической схемой. Для строки w ∈ (N ∪ T )
∗
определим язык L(G, w) = {x ∈ T
∗
| w =⇒
∗
x}, где вывод
производится в соответствии с продукциями из P .
Универсальная грамматика типа 0 — это грамматическая
схема G
u
= (N
u
, T
u
, P
u
), где N
u
, T
u
— непересекающиеся ал-
фавиты, а P
u
— конечное множество пер еписыв ающих правил

3.3. Универсальные машины Тьюринга 149
над N
u
∪ T
u
, которая обладает таким свойством: для каждой
грамматики G = (N, T
u
, S, P ) типа 0 существует такая строка
w(G), что L
G
u
, w(G)
= L(G).
Итак, универсальная грамматика моделирует любую напе-
ред заданную грамматику G при условии, что код w(G) послед-
ней берется в качестве аксиомы универсальной грамматики.
Универсальные грамматики типа 0 в описанном выше смыс-
ле существуют. Так как это утверждение лежит в основе после-
дующих рассмотрений, приведем его полное доказательство.
Пусть G = (N, T, S, P ) — гр амматика типа 0. Без огра-
ничения общности можно предполагать, что нетерминальных
символов всего три, N = {S, A, B}. (Если их больше, скажем
N = {S, X
1
, X
2
, . . . , X
n
}, где n > 3, то заменим каждое вхо-
ждение X
i
в правила из P на AB
i
A, 1 6 i 6 n, для каких-то
новых символов A, B. Очевидно, что полученная грамматика
будет эквивалентна исходной.)
Построим грамматическую схему
G
u
= (N
u
, T, P
u
),
в которой
N
u
= {A, B, C, D, E, F, H, R, Q, S, X, Y }
∪ {[a, i] | a ∈ T, 1 6 i 6 9},
а множество P
u
состоит из следующих правил:
(I) (1) C → BQ,
(2) Qα → αQ для α ∈ N ∪ T ∪ {D, E},
(II) (3) QDα → [α, 2]D[α, 1] для α ∈ N ∪ T ,
(4) α[β, 2] → [β, 2]α для α ∈ N ∪ T ∪ {D, E}, β ∈ N ∪ T ,
(5) B[α, 2] → [α, 3]B для α ∈ N ∪ T ,
(6) α[β, 3] → [β, 3]α для α, β ∈ N ∪ T ,
(7) α[α, 3] → [α, 4] для α ∈ N ∪ T ,
(III) (8) [α, 1]β → [β, 5][α, 1][β, 1] для α, β ∈ N ∪ T ,
(9) α[β, 5] → [β, 5]α для α ∈ N ∪ T ∪ {D, E}, β ∈ N ∪ T ,
(10) B[α, 5] → [α, 6]B для α ∈ N ∪ T ,

150 3. Введение в теорию языков
(11) α[β, 6] → [β, 6]α для α, β ∈ N ∪ T ,
(12) [α, 4]β[β, 6] → [α, 4] для α , β ∈ N ∪ T ,
(IV) (13) [α, 1]Eβ → [α, 7]E[β, 9] для α, β ∈ N ∪ T,
(14) [α, 1][β, 7] → [α, 7]β для α, β ∈ N ∪ T,
(15) D[α, 7] → Dα для α ∈ N ∪ T,
(16) [α, 9]β → [β, 8][α, 9][β, 9] для α, β ∈ N ∪ T,
(17) α[β, 8] → [β]α для α ∈ N ∪T ∪{B, D, E}, β ∈ N ∪ T ,
(18) [α, 9][β, 8] → [β, 8][α, 9] для α, β ∈ N ∪ T,
(19) [α, 4][β, 8] → β[α, 4] для α, β ∈ N ∪ T,
(V) (20) [α, 1]ED → [α , 7]RED для α ∈ N ∪ T,
(VI) (21) [α, 9]D → RαD для α ∈ N ∪ T,
(22) [α, 9]R → Rα дл я α ∈ N ∪ T,
(23) αR → Rα для α ∈ N ∪ T ∪ {D, E},
(24) BR → RC,
(25) [α, 4]R → λ для α ∈ N ∪ T
(VII) (26) Aα → αA для α ∈ T,
(27) AC → H,
(28) Hα → H для α ∈ N ∪ T ∪ {D, E},
(29) HF → λ.
Допустим, что P = {u
i
→ v
i
| 1 6 i 6 k}, и рассмотрим
code(G) = ASCDu
1
Ev
1
Du
2
Ev
2
D · · · Du
k
Ev
k
DF.
Сперва проверим, как грамматическая схема G
u
действует
на строках вида AwCDu
1
Ev
1
D · · · Du
k
Ev
k
DF .
Группа правил (I) вводит нетерминальный символ Q, кото-
рый выбирает правило вывода u
i
→ v
i
, расположенное справа
от нетерминального символа D (по правилу (3)). По второй
группе правил первый символ α слова u
i
преобразуется в [α, 1]
и нетерминальный символ [α, 2], который движется влево, пока
не окажется слева от B, где он превращается в [α, 3]. Если в w
есть вхождение α, то по правилу (7) вводится нетерминальный
символ [α, 4] для того, чтобы закодировать эту информацию.
