Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений
Подождите немного. Документ загружается.


3.3. Универсальные машины Тьюринга 151
Правила третьей группы заменяют все символы β в слове
u
i
на [β, 1], а затем каждый такой символ β справа от [α, 4]
стирается, если это возможно сделать с соблюдением порядка.
Тем самым, обнаруживается вхождение слова u
i
в слово w.
По правилам группы (IV) каждый символ β из v
i
6= λ пре-
образуется в [β, 9] и [β, 8]. Последний символ сдвигается влево,
пока не окажется слева от B. Когда [β, 8] достигнет [α, 4], вво-
дится символ β. Тем самым, стертая правилами группы (III)
строка u
i
заменяется на v
i
. Если v
i
= λ, то вместо правил груп-
пы (IV) испол ьзуется правило (20). Таким образом, получаем
шаг вывода w =⇒ w
0
, использующий правило u
i
→ v
i
.
Эта проц едура может повторяться благодаря правилам
группы (VI). Если w
0
содержит вспомогательные символы, то
по правилам группы (VII) все их можно стереть, оставив лишь
терминальные. Следовательно, L(G) ⊆ L
G
u
, code(G)
.
Для того чтобы доказать обратное включение, заметим, что
удалить нетерминальный символ A можно лишь в том случае,
когда межд у A и C стоит терминальная строка. Каждый шаг
вывода обязан начинаться с введения символа Q. Стирание это-
го символа влечет появление нетермин альн ого символа [α, 1],
который в свою очередь может пропасть лишь при замене его
на [α, 9]. Эти операции возможны тогда и только тогда, когда
подстрока u
i
удаляется и з w. Удаление [α, 9] возможно лишь
после записи строки v
i
на месте стертой u
i
. Появляющийся при
этих действиях символ R можно удалить, только когда строка
приобретет вид Aw
0
CDu
1
Ev
1
D . . . Du
k
Ev
k
DF . Тем самым мо-
делируется шаг вывода, использующий правило u
i
→ v
i
. Все
выводы другого вида заблокированы в G
u
. Таким образом, по-
лучено включение L
G
u
, code(G)
⊆ L(G), что завершает до-
казательство равенства L
G
u
, code(G)
= L(G).
Заметим, что построенная выше универсальная граммати-
ка G
u
кодирует то, как используется грамматика G в процессе
вывода: выбор правила, удаление вхождения его левого члена,
запись на это место правого члена правила, проверка того, со-
стоит ли полученная строка лишь из терминальных символов.

152 3. Введение в теорию языков
Здесь возникает естественный вопрос, важный и дл я моле-
кулярных вычислений: справедл ивы ли результаты об универ-
сальности также и для других классов а втоматов и грамматик,
отличных от машин Тьюринга и грамматик типа 0, в частно-
сти, для конечных автоматов.
Если понимать этот вопрос в строгом смысле, то ответ на
него отрицателен: нет конечного автомата, унив ерсаль ного для
класса всех конечных автоматов. Тому есть две причины. Во-
первых, невозможно закодировать с помощью конечного авто-
мата то, как конечный автомат обрабатывает входную строку
(пришлось бы запоминать символы входной строки, не помечая
их, а этого невозможно добиться, имея лишь конечное множе-
ство состояний). Во-вторых, невозможно закодировать состо-
яния произвольного данного конечного автомата так, чтобы
оперировать с ним, исходя из конечного множества состояний
универсального автомата (сколь угодно большое множество со-
стояний приводит к кодам сколь угодно большой длины, так
что информация, содержащаяся в них, опять-таки не вмещает-
ся в фиксированное конечное множество состояний).
Однако для наших целей достаточно построить универсаль-
ный автомат в следующем ослабленном смысле. Рассмотрим
класс конечных автоматов, у которых множество состояний
и входной алфавит являются подмножествами конечных мно-
жеств K и V , соответств енно. Для этого класса уже можно
сконструировать универсальный конечный автомат.
Рассмотрим следующий конечный автомат
M
u
= (K
u
, V ∪ K ∪ {c
1
, c
2
}, q
0,u
, F
u
, P
u
),
в котором
K
u
= {q
0,u
, q
0
0,u
, q
00
0,u
, q
f
}
∪ {[s], (s), (s)
0
, (s)
00
,
(s), (s)
0
, (s)
00
, (s)
000
| s ∈ K}
∪ {[sa], [sas
0
], [sas
0
]
0
, [sas
0
]
00
, [sas
0
]
000
, [sas
0
]
iv
| s, s
0
∈ K, a ∈ V },
F
u
= {q
f
},

3.3. Универсальные машины Тьюринга 153
а P
u
содержит следующие правила перехода:
1. q
0,u
s → sq
0
0,u
, s ∈ K,
q
0
0,u
a → aq
00
0,u
, a ∈ V,
q
00
0,u
s → sq
0,u
, s ∈ K,
2. q
0,u
s
0
→ s
0
[s
0
],
[s
0
]a → a[s
0
a], a ∈ V,
[s
0
a]s → s[s
0
as], s ∈ K , a ∈ V,
3. [sas
0
]s
00
→ s
00
[sas
0
]
0
, s, s
0
, s
00
∈ K, a ∈ V,
[sas
0
]
0
b → b[sas
0
]
00
, s, s
0
∈ K, a, b ∈ V,
[sas
0
]
00
s
00
→ s
00
[sas
0
], s, s
0
, s
00
∈ K, a ∈ V,
[sas
0
]c
1
→ c
1
[sas
0
]
000
, s, s
0
∈ K, a ∈ V,
[sas
0
]
000
s
00
→ s
00
[sas
0
]
000
, s, s
0
, s
00
∈ K, a ∈ V,
[sas
0
]
000
c
2
→ c
2
[sas
0
]
iv
, s, s
0
∈ K, a ∈ V,
4. [sas
0
]
iv
a → a(s
0
), s, s
0
∈ K, a ∈ V,
5. (s)s
0
→ s
0
(s)
0
, s, s
0
∈ K,
(s)
0
a → a(s)
00
, s ∈ K, a ∈ V,
(s)
00
s
0
→ s
0
(s), s, s
0
∈ K,
6. (s)s → s[s], s ∈ K,
[s]a → a[sa], s ∈ K, a ∈ V,
[sa]s
0
→ s
0
[sas
0
], s, s
0
∈ K, a ∈ V,
7. (s)s
0
→ s
0
(s)
0
, s, s
0
∈ K,
(s)s
0
→ s
0
(s)
0
, s, s
0
∈ K,
(s)
0
a → a(s)
00
, s ∈ K, a ∈ V,
(s)
00
s
0
→ s
0
(s), s, s
0
∈ K,
(s)c
1
→ c
1
(s)
000
, s ∈ K,
(s)
000
s
0
→ s
0
(s)
000
, s, s
0
∈ K, s 6= s
0
,
(s)
000
s → sq
f
, s ∈ F,
q
f
s → sq
f
, s ∈ K,
q
f
c
2
→ c
2
q
f
.

154 3. Введение в теорию языков
Для конечного автомата M = (K, V, s
0
, F, P ) рассмотрим
строку code(M) = s
1
a
1
s
0
1
s
2
a
2
s
0
2
· · · s
n
a
n
s
0
n
c
1
s
f1
s
f2
· · · s
fm
c
2
, где
s
i
a
i
→ a
i
s
0
i
∈ P , 1 6 i 6 n, каждая строка s
i
a
i
s
0
i
встречается
лишь однажды, {s
f1
, . . . , s
fm
} = F , а c
1
, c
2
— новые символы.
Для пары строк z, x ∈ V
∗
, где x = a
1
a
2
. . . a
p
, a
i
∈ V ,
1 6 i 6 p, опр едели м операцию блочной перетасовки равен-
ством
bls(z, x) = za
1
za
2
. . . za
p
z.
Автомат M
u
является универсальным для класса конечных
автоматов вида M = (K
0
, V
0
, s
0
, F, P ), где K
0
⊆ K, V
0
⊆ V , в
следующем смысле: bls(code(M ), x) ∈ L(M
u
), тогда и только
тогда, когда x ∈ L(M).
Действительно, автомат M
u
работает так: когда он нахо-
дится в начальном состоянии q
0,u
или в состоянии вида (s),
он просматривает code(M ), пропуская несколько блоков вида
s
i
a
i
s
0
i
; затем запоминает один блок такого типа, переходя в со-
стояние [s
i
a
i
s
0
i
] (если цикл начат с q
0,u
, то s
i
= s
0
); далее ав-
томат пропускает оставшиеся блоки s
j
a
j
s
0
j
и проходит через
c
1
s
f
1
· · · s
f
m
c
2
(переходя при это м в состояние [s
i
a
i
s
0
i
]
iv
); пра-
вило s
i
a
i
→ a
i
s
0
i
автомата M моделируется правилом типа 4,
которое переводит автомат M
u
в состояние вида (s); цикл по-
вторяется |x| раз; правила группы 7 обеспечивают то, что в
состояние q
f
автомат M
u
перейдет лишь тогда, когда промо-
делирует обработку слова x автоматом M, завершающуюся в
состоянии из F .
Мы закончим двумя наблюдениями, касающимися универ-
сального автомата M
u
. Во-первых, описанную выше конструк-
цию можно рассматривать и для бесконечных множеств K и V .
Такой автомат M
u
можно считать универсальным для всех
конечных автоматов. При этой модификации M
u
, разумеет-
ся, уже не будет конечным автоматом, хотя его схематическое
определение очень просто. (Такие обобщения конечных авто-
матов часто обсуждались на заре развития теории автоматов.)
Во-вторых, в нашей конструкции описание конкретного мо-
делируемого автомата, code(M), нужно записывать во входной
строке автомата M
u
несколько раз. Этого можно избежать, ес-

3.3. Универсальные машины Тьюринга 155
ли снабдить M
u
двумя лентами и позволить читающей головке
передвигаться в обоих направлениях. Подробности такой мо-
дификации мы опускаем.
3.4 Комментарии к библиографии
Некоторые из книг по теории формальных языков упомянуты
в разделе 3.1; ряд других можно найти в списке литературы.
Мы не указываем здесь источники для результатов разде-
ла 3.1.
Теорема 3.12 является классической, она содержится в
большинстве монографий по теории формальных языков. Тео-
рема 3.13 появилась в [174]; следствие 3.3 установлено в [20]
как усиление более раннего результата о том, что каждый
рекурсивно перечислимый язык является образом пересечения
двух контекстно-свободных языков при некотором морфизме.
Результаты типа теоремы 3.14 имеются в [235, 290, 338].
Характеризации рекурсивно перечисл имых языков, осно-
ванные на множествах совпадений морфизмов получены в [306,
58]; конструкция в теореме 3.15 взята из [307], где можно найти
все подробности. Вариант теоремы 3.15, приведенный в теоре-
ме 3.16, был доказан в [159]. Теорема 3.17 и ее следствие 3.4 до-
казаны в [84]. Теорема 3.18 взята из [83]. Сходные (но несколь-
ко более слабые) результаты появлялись также и в [32]. Языки
перетасованных полукопий рассматривались в [213], откуда за-
имствованы теорема 3.19 и следствие 3.5.
Конструкции универсальных машин Тьюринга имеются
в [223, 313] и (в большом числе) в [284]. Конструкция универ-
сальной грамматики типа 0 в разделе 3.3 взята из [35]; она
имеется также и в [34].
Глава 4
Системы со склейкой
Основными структурами данных в теории формальных языков
являются слова, т. е. строки элементов, букв. Идея «строки»
состоит в том, чтобы наделить элементы линейным порядком.
Двойная спираль ДНК, рассматриваемая, как мы это делали
выше, в виде двумерного объекта, представляет собой струк-
туру данных нового типа: двойную цепо чку. Хотя обе состав-
ляющие ее одинарные цепочки по-прежнему остаются линейно
упорядоченными строками элементов, двойная цепочка обла-
дает важн ым дополнительным свойством: спаренные элементы
цепочек комплементарны относительно некоторого фиксиро-
ванного симметричного отношения. Мы уже обсуждали взаи-
мосвязи между комплементарностью Уотсона–Крика и языком
перетасованных копий и обращали внимани е на вычислитель-
ный потенциал последнего. В данн ой и следующей главах мы
постоянно будем пользоваться этими наблюдениями. Пр и этом
полученные выше характеризации рекурсивно перечислимых
языков, основанные на множествах совпадений и языках пере-
тасованных копий, найдут весьма естественные приложения.
4.1 Операция склеивания
Начнем с формализации основной операции, с п омощью кото-
рой двойные цепочки строятся из «ДНК-домин о», т. е. из после-
довательностей с липкими концами с одной или с обеих сторон
или из одинарных цепочек, присоединяющихся друг к другу
при ренатурации и сшивке.
Рассмотрим алфавит V и симметричное отношение компле-
ментарности ρ ⊆ V × V на V . Заметим, что хотя свойство
симметрии не используется в дальнейшем, мы все же пред-
полагаем симметричность отношения ρ, поскольку комплемен-

4.1. Операция склеивания 157
тарность Уотсона–Крика симметрична (и вообще, интуитивная
идея комплементарности подразумевает симметричность).
Свяжем с алфавитом V , помимо моноида V
∗
, состоящего
из строк над V , моноид пар строк V
∗
× V
∗
. Согласно способу
представления молекул ДНК, при котором две цепочки распо-
лагаются одна над другой, запишем элементы (x
1
, x
2
) ∈ V
∗
×V
∗
в виде
x
1
x
2
. Тогда произведением двух пар
x
1
x
2
,
y
1
y
2
будет
x
1
y
1
x
2
y
2
. Кроме того, вместо V
∗
× V
∗
будем писать
V
∗
V
∗
. Еди-
ничный элемент
λ
λ
из
V
∗
V
∗
часто отождествляется с λ и
опускается, если он несуществен в данном контексте. Обозна-
чим также
V
V
ρ
= {
h
a
b
i
| a, b ∈ V, (a, b) ∈ ρ}, WK
ρ
(V ) =
V
V
∗
ρ
.
Множество WK
ρ
(V ) называется областью Уотсона–Крика,
ассоциированной с алфавитом V и отношением комплементар-
ности ρ. Элемент
h
a
1
b
1
ih
a
2
b
2
i
· · ·
h
a
n
b
n
i
∈ WK
ρ
(V ) можно записы-
вать в виде
h
w
1
w
2
i
, где w
1
= a
1
a
2
· · · a
n
, w
2
= b
1
b
2
· · · b
n
. Назовем
такие элементы
h
w
1
w
2
i
∈ WK
ρ
(V ) двойными цепочками правиль-
ной формы или прост о двойными цепочками (или молекулами,
напоминая, что ими моделируется). Две компоненты молекулы
также называются цепочками: w
1
— верхней, а w
2
— нижней.
По определению WK
ρ
(V ) элемент
h
λ
λ
i
тоже является моле-
кулой, хотя для него и нет никакого биохимического представ-
ления. Таким образом, WK
ρ
(V ) — моноид. Для любых двух его
элементов
h
x
1
x
2
i
и
h
y
1
y
2
i
, последовательность
h
x
1
y
1
x
2
y
2
i
имеет пра-
вильную форму, а, значит, лежит в WK
ρ
(V ).
Отметим существенное различие между
x
y
и
h
x
y
i
:
x
y
яв-
ляется лишь другим обозначением пары (x, y), что не предпо-
лагает связи между соответствующими символами строк x и
y, тогда как
h
x
y
i
представляет собой молекулу с предписанной
связью между соответствующими символами ее цепочек. Эта

158 4. Системы со склеиванием
связь определяется отношением комплементарности ρ на алфа-
вите V , поэтому для полного описания всех этих деталей мы
обычно будем писать
h
x
y
i
∈ WK
ρ
(V ), хотя и сама запись
h
x
y
i
уже говорит нам, что рассматривается молекула.
Особо подчеркнем два свойства, характеризующих элемен-
ты
h
w
1
w
2
i
из WK
ρ
(V ), поскольку они важны для моделей, рас-
сматриваемых в этой и следующей главах:
1. длины нитей w
1
и w
2
одинаковы,
2. соответствующие символы нитей комплементарны в смысле
отношения ρ.
Это довольно сильные свойства. Мы увидим, что используя
элементы из WK
ρ
(V ), легко получить характеризации RE . В
действительности, пересечение «встроено» в определение об-
ласти Уотсона–Крика. Отметим, однако, что молекулы ДНК
обеспечивают эти свойства «даром»: они на самом деле суть
двойные цепочки правильной формы, корректность которых
проверяется самой природой.
Ниже мы будем использовать и «неполн ые молекулы», т. е.
элементы множества
W
ρ
(V ) = L
ρ
(V ) ∪ R
ρ
(V ) ∪ LR
ρ
(V ),
где
L
ρ
(V ) = (
λ
V
∗
∪
V
∗
λ
)
V
V
∗
ρ
,
R
ρ
(V ) =
V
V
∗
ρ
(
λ
V
∗
∪
V
∗
λ
),
LR
ρ
(V ) = (
λ
V
∗
∪
V
∗
λ
)
V
V
+
ρ
(
λ
V
∗
∪
V
∗
λ
).
Здесь, когда мы пишем, например,
u
λ
h
x
y
i
, подразумева-
ется лишь выражение, полученное сцеплением двух символов
u
λ
и
h
x
y
i
. Его нельзя заменить, скажем, на
ux
y
, поскольку
пропадет информация об отношении комплементарности меж-
ду символами из x и y. Обозначение
ux
y
применимо к любой
4.1. Операция склеивания 159
y
x
y
x
y
x
y
x
y
x z
y
x z
zx
y
zx
y
L
ρ
(V ):
R
ρ
(V ):
LR
ρ
(V ):
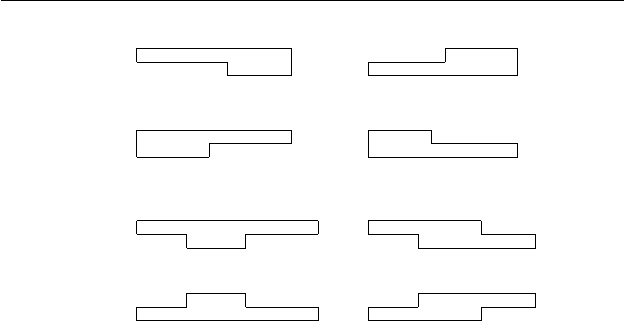
Рис. 4.1. Возможные формы «домино».
паре строк, тогда как
h
x
y
i
обозначает молекулу. Если u 6= λ, то
выражение
h
ux
y
i
просто не определено.
Возможные формы элементов из W
ρ
(V ) изображены на
рис. 4.1. Во всех случаях можно увидеть двойную цепочку x
правильной формы и отростки y, z по одну или по обе стороны
от x. Эти отростки (липкие концы) могут располагаться в
верхней или в нижней цепочках. Отметим, что в элементах
множеств L
ρ
(V ) и R
ρ
(V ) блок x может быть пустым, но в
элементах из LR
ρ
(V ) выполняется условие x ∈
h
V
V
i
+
ρ
, т. е.
в x должен быть по крайней мере один такой элемент
a
b
,
что (a, b) ∈ ρ. И наконец, отростки могут отсутствовать, то-
гда получится элемент из WK
ρ
(V ), следовательно WK
ρ
(V )
содержится в каждом из множеств L
ρ
(V ), R
ρ
(V ), LR
ρ
(V ).
Элемент множества W
ρ
(V ), у которого по крайней мере в
одной позиции стоит
a
b
, a 6= λ, b 6= λ, называется двойной це-
почкой с правильной основой. Разумеется, в нем все вхождения
«столбиков»
a
b
, где (a, b) ∈ ρ, располагаются подряд. Прои з-
вольный элемент из W
ρ
(V ) на зывают домино (более точным
термином было бы полимино).

160 4. Системы со склеиванием
На множестве W
ρ
(V ) определим частичную операц ию,
моделирующую операцию сшивки. К молекуле с правильной
основой можно слева или справа присоединить домино, если их
липкие концы сочетаются, т. е. на соответствующих позициях
стоят комплементарные символы. Результатом такой операции
всегда будет молекула с правильной основой, т. е. без пустых
мест, окруженных символами из V .
Более подробно, рассмотрим молекулу с правильной осно-
вой x ∈ W
ρ
(V ) и домино y ∈ W
ρ
(V ). Молекулу x можно (оче-
видно, единственным способом) представить в виде x = x
1
x
2
x
3
,
где x
2
∈ WK
ρ
(V ) − {
h
λ
λ
i
} и x
1
, x
3
∈
V
∗
λ
∪
λ
V
∗
.
Склейка x и y, обозначаемая µ(x, y), определена в след ую-
щих случаях:
(1) x
3
=
u
λ
, y =
λ
v
y
0
для таких u, v ∈ V
∗
, что
u
v
∈ WK
ρ
(V ) и y
0
∈ R
ρ
(V ); тогда µ(x, y) = x
1
x
2
u
v
y
0
;
(2) x
3
=
λ
v
, y =
u
λ
y
0
для таких u, v ∈ V
∗
, что
u
v
∈ WK
ρ
(V ) и y
0
∈ R
ρ
(V ); тогда µ(x, y) = x
1
x
2
u
v
y
0
;
(3) x
3
=
u
1
λ
, y =
u
2
λ
для u
1
, u
2
∈ V
∗
; тогда
µ(x, y) = x
1
x
2
u
1
u
2
λ
;
(4) x
3
=
u
1
u
2
λ
, y =
λ
v
для таких u
1
, u
2
, v ∈ V
∗
, что
u
1
v
∈ WK
ρ
(V ); тогда µ(x, y) = x
1
x
2
u
1
v
u
2
λ
;
(5) y =
λ
v
1
v
2
для таких u, v
1
, v
2
∈ V
∗
, что
h
u
v
1
i
∈ WK
ρ
(V );
тогда µ(x, y) = x
1
x
2
h
u
v
1
i
λ
v
2
;
(6) x
3
=
λ
v
1
, y =
λ
v
2
для v
1
, v
2
∈ V
∗
; тогда
µ(x, y) = x
1
x
2
λ
v
1
v
2
,
(7) x
3
=
λ
v
1
v
2
, y =
u
λ
для таких u, v
1
, v
2
∈ V
∗
, что
h
u
v
1
i
∈ WK
ρ
(V ); тогда µ(x, y) = x
1
x
2
h
u
v
1
i
λ
v
2
;
(8) x
3
=
λ
v
, y =
u
1
u
2
λ
для таких u
1
, u
2
, v ∈ V
∗
, что
u
1
v
∈ WK
ρ
(V ); тогда µ(x, y) = x
1
x
2
u
1
v
u
2
λ
