Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений
Подождите немного. Документ загружается.

4.1. Операция склеивания 161
x
y
x
y
xxx
y
y y
y
x
y
x
y
x
(1) (2)
(3)
(6) (7)
(4) (5)
(8)
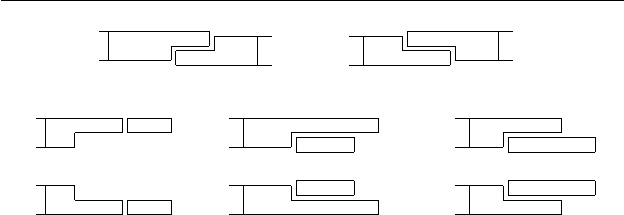
Рис. 4.2. Операция склейки.
Эти восемь случаев изображены на рис. 4.2.
Симметрично можно определ ить µ(y, x), присоединяя к мо-
лекуле с правильной основой x последовательность y слева. От-
метим, что нет нужды по-разному обозначать «левую» и «пра-
вую» склейки. В обоих случаях по крайней мере один из тер-
мов операции должен быть молекулой с правильной основой, а
результат (тоже молекула с правильной основой) целиком за-
висит от порядка последовательностей и их липких концов.
Отметим, что во всех случаях допустимы соединения и
«прямыми» концами, т. е. концами без отростков. При этом
всегда пол учается двойная цепочка с пр ави льно й основой (ее
подпоследовательность из WK
ρ
(V ) не обязательно длиннее,
чем подпоследовательность x
2
∈ WK
ρ
(V ) из x).
В случаях 3 и 6 не исп оль зуется ренатурация, а, значит, и
отношение комплементарности. Операцию, которая получится,
если исключить эти случаи из определения µ(x, y), мы обозна-
чим через µ
0
(x, y) и назовем ограниченной склейкой.
Максимальную длину отростка в цепочке z ∈ W
ρ
(V ) назы-
вают задержкой для z и обозначают через d(z). (Видно, что
в случаях 1, 2 на р ис. 4.2, т. е. если y тоже является двойной
цепочкой с правильной основой, «правая задержка» для x и
«левая задержка» для y должны совпадать.)
Подобно тому как переписывание лежит в основе грамма-
тик Хомского, склейка служит основной операцией в системах
со склейкой, исследуемых в следующих разделах.

162 4. Системы со склейкой
4.2 Системы со склейкой: классификация
Здесь мы определим системы со склейкой в наиболее общем ви-
де: когда молекулы строятся, исходя из цепочки с правильной
основой, которая удлиняется в обоих направлени ях с исполь-
зованием домино произвольных форм и операции µ. Ниже мы
увидим, что системы более специфических типов равносиль-
ны системам общего вида по модулю таких сжимающих ме-
ханизмов, как слабое кодирование и детерминированное ОПМ-
отображение.
Система со склейкой — это четверка
γ = (V, ρ, A, D),
в которой V — алфавит, ρ ⊆ V ×V — симметричное отношение,
A — конечное подмножество множества LR
ρ
(V ), D — конечное
подмножество множества W
ρ
(V ) × W
ρ
(V ).
Отношение ρ — это отношение комплементарности на мно-
жестве V , элементы из A называются аксиомами. Начав с акси-
ом и используя пары (u, v) домино из D, при помощи операции
склейки µ получают некоторое множество двой ных цепочек из
WK
ρ
(V ), т. е. «полных» молекул.
Формально, для данной системы γ = (V, ρ, A, D) и двух по-
следовательностей x, y ∈ LR
ρ
(V ) запишем
x =⇒ y тогда и только тогда, когда y = µ
u, µ(x, v)
для
некоторого (u, v) ∈ D.
Очевидно, что µ
u, µ(x, v)
= µ
µ(u, x), v
, поскольку удли не-
ние влево не зависит от удлинения вправо.
Последовательность x
1
=⇒ x
2
=⇒ . . . =⇒ x
k
, где x
1
∈ A,
называется вычислением в γ. Вычисление σ : x
1
=⇒
∗
x
k
яв-
ляется завершенным, если x
k
∈ WK
ρ
(V ) (у заключительной
цепочки нет липких концов, а значит, нет и пробелов).
Множество всех молекул над V , получившихся в кон-
це всех завершенных вычислений в γ, обозначается через
LM
n
(γ). Здесь LM — аббревиатура от слов «Language of
Molecules» (язык молекул), а индекс n произведен от слова
«non-restricted» (неограниченный): вычисления не ограничены

4.2. Системы со склейкой: классификация 163
ничем, кроме того, что они должны быть завершенными. Итак,
LM
n
(γ) = {w ∈ WK
ρ
(V ) | x =⇒
∗
w, x ∈ A}.
В дальнейшем системы со склейкой рассматриваются как
генераторы языков строк. Для этого свяжем с LM
n
(γ) язык
L
n
(γ) =
n
w ∈ V
∗
|
h
w
w
0
i
∈ LM
n
(γ) для некоторого w
0
∈ V
∗
o
.
Будем говорить, что язык L
n
(γ) порожден γ.
Интересны и некоторые типы ограниченных вычислений.
Говорят, что завершенное вычисление x
1
=⇒ x
2
=⇒ . . . =⇒ x
k
:
примитивно, если ни для какого i, 1 6 i < k, не выполняется
включение x
i
∈ WK
ρ
(V ), т. е. x
k
— первая полная молекула
в этом вычислении);
имеет з адержку d, если d(x
i
) 6 d для каждого 1 6 i 6 k.
Обозначим через L
p
(γ) и L
d
(γ), d > 1, языки, порождаемые
γ в результате при митивн ых вычи слени й и соответствен но вы-
числений с задержкой d.
Как и L
n
(γ), языки L
p
(γ), L
d
(γ) состоят из строк, распо-
ложенных в верхних цепочках молекул, порождаемых γ, но
мы не вдаемся в детали соотношений между языками L
α
(γ) и
LM
α
(γ), где α ∈ {n, p, d}, поскольку здесь мы вообще не иссле-
дуем языки молекул. В действительности, соотношение между
L
α
(γ) и LM
α
(γ) зависит от ρ. Например, если ρ — инъективное
отображение, то язык молекул LM
α
(γ) однозначно определяет-
ся языком строк L
α
(γ), а если ρ — произвольное симметрич ное
отношение, то L
α
(γ) есть образ LM
α
(γ) при кодировании, а
LM
α
(γ) — образ L
α
(γ) при обратном кодировании.
Ясно, что выполняются следующие включения:
L
p
(γ) ⊆ L
n
(γ),
L
d
1
(γ) ⊆ L
d
2
(γ), если 1 6 d
1
6 d
2
,
L
d
(γ) ⊆ L
n
(γ) для всех d > 0.
Говорят, что система γ имеет ограниченную задержку, если
существует такое d > 1, что L
d
(γ) = L
n
(γ).

164 4. Системы со склейкой
Представляют интерес и некоторые частные типы систем
со склейкой. Говорят, что система γ = (V, ρ, A, D):
односторонняя, если u = λ или v = λ в каждой паре (u, v) ∈ D;
регулярная, если u = λ в каждой паре (u, v) ∈ D;
простая, если для всех пар (u, v) ∈ D либо u, v ∈
V
∗
λ
, либо
u, v ∈
λ
V
∗
.
В односторонних системах удлинения влево и вправо неза-
висимы. В регулярных системах допустимы лишь удлинения
последовательностей вправо (следовательно, аксиомы должны
иметь вид x
1
x
2
, где x
1
∈ WK
ρ
(V ) и x
2
∈
V
∗
λ
∪
λ
V
∗
). При
вычислениях в простой системе символы добавляются только
к одной из компонент двойной цепочки.
Обозначим через ASL(α) семейство языков вида L
α
(γ), где
α ∈ {n, p}, а γ — система общего вида. Здесь SL — аббреви-
атура слов «Sticker Language» (язык наклеек), а A (от сло-
ва «Arbitrary» — произвольный) показывает, что речь идет о
системе общего вида. Семейство языков, порождаемых систе-
мами с ограниченной задержкой, обозначается через ASL(b).
Если используются только односторонние, или только регуляр-
ные, или только простые, или толь ко простые и односторонние,
или только простые и регулярные системы, то заменим символ
A перед SL(α) на O, R, S, SO, SR соответственно. Подчерк-
нем, что все эти семейства состоят из языков строк, а не моле-
кул, поэтому можно безо всяких оговорок обсуждать их соот-
ношения с семействами из иерархии Хомского. Это не совсем
так для семейств языков вида LM
α
(γ), поскольку при работе
с ними приходится учитывать отношение комплементарности
ρ. Как отмечено выше, при инъективном ρ язык LM
α
(γ) изо-
морфен L
α
(γ), но если ρ не инъективно, то нужно принимать
во внимание кодирование, связывающее LM
α
(γ) и L
α
(γ).
Из определений следует:
Лемма 4.1. Для каждого α ∈ {n, p, b} выполняются соотно-
шения, изображенные на рис. 4.3, на котором стрелки озна-
чают не обязательно строгие включения.

4.2. Системы со склейкой: классификация 165
SRSL(α)
@
@
@I
RSL(α)SOSL(α)
@
@
@I
OSL(α)
@
@
@I
@
@
@I
ASL(α)
SSL(α)
Рис. 4.3. Соотношения между семействами языков,
порождаемых склеивающими системами (предварительные
результаты).
Лемма 4.2. Для каждого X ∈ {A, O, R, S, SO, SR} выполня-
ется включение XSL(b) ⊆ XSL(n).
В силу отсутствия стирающих операций непосредственно
получается следующий результат.
Лемма 4.3. XSL(α) ⊆ CS для всех вышеописанных X и α.
Перед тем, как приступить к исследованию размеров се-
мейств XSL(α), рассмотрим два примера. Первый из них —
пример простой склеивающей системы:
γ
1
= (V, ρ, A, D),
V = {a, b, c},
ρ = {(a, a), (b, b), (c, c)},
A = {
h
a
a
i
},
D = {(
b
λ
,
b
λ
), (
c
λ
,
λ
λ
),
(
λ
b
,
λ
λ
), (
λ
c
,
λ
b
)}.

166 4. Системы со склейкой
Здесь
WK
ρ
(V ) =
h
a
a
i
,
b
b
,
h
c
c
i
∗
,
но в силу структуры пар множества D порождаться могут
лишь цепочк и вида x
a
a
h
b
b
i
m
, где x ∈ {
h
b
b
i
,
c
c
}
∗
. Более того,
цепочка x должна содержать ровно m вхождений
h
b
b
i
и ров-
но m вхождений
c
c
. Следовательно, язык L
n
(γ
1
) не является
контекстно-свободным:
LM
n
(γ
1
) ∩
h
c
c
i
+
b
b
+
h
a
a
i
b
b
+
=
h
c
c
i
m
b
b
m
h
a
a
i
b
b
m
| m > 1
,
L
n
(γ
1
) ∩ c
+
b
+
ab
+
= {c
m
b
m
ab
m
| m > 1}.
Работая сначала с верхней цепочкой, т. е. используя пары
(
b
λ
,
b
λ
), (
c
λ
,
λ
λ
), а только затем с нижн ей, можно по-
лучить каждую цепочку из LM
n
(γ
1
) с помощью примитивных
вычислений, откуда L
p
(γ
1
) = L
n
(γ
1
).
Это не так для вычислений с ограниченной задержкой. Дей-
ствительно, цепочку вида
c
c
m
h
b
b
i
m
a
a
h
b
b
i
m
невозможно со-
здать с задержкой меньше чем m/2, поскольку нельзя исполь-
зовать пару (
λ
c
,
λ
b
) до того, как пара (
λ
b
,
λ
λ
) будет
использована m раз, но к этому моменту б удет уже выработа-
на последовательность вида
λ
b
p
h
b
b
i
q
a
a
b
q
λ
для p + q = m,
т. е. задержка будет не меньше, чем m/2.
Итак, L
d
(γ
1
) ⊂ L
n
(γ
1
) для всех d > 1. Все языки L
d
(γ
1
) ли-
нейны. Мы не будем это доказывать для системы γ
1
, поскольку
это следует из одного общего результата следующего раздела.
Рассмотрим еще одну систему (уже не простую):
γ
2
= (V, ρ, A, D),
V = U ∪
U ∪ U
0
для некоторого алфавита U,
ρ = {(a, a), (¯a, ¯a), (a
0
, a
0
) | a ∈ U },

4.3. Выразительная сила систем со склейкой 167
A = {
a
0
0
a
0
0
} для некоторого фиксированного a
0
∈ U,
D = {(
a
0
λ
,
h
a
a
i
), (
λ
a
0
,
h
¯a
¯a
i
) | a ∈ U }.
Начинаем со столбика
h
a
0
0
a
0
0
i
для фиксированного a
0
∈ U и стро-
им молекулу, добавляя справа от него столбики
a
a
,
¯a
¯a
; одно-
временно слева от него появляются символы a
0
, причем появ-
ление такого символа в верхней цепочке соответствует добав-
лению справа столбика
a
a
, а в нижней цепочке — столбика
¯a
¯a
. Это означает, что по (модулю штрихов и надчеркиваний)
цепочка столбиков
h
a
0
a
0
i
слева от
h
a
0
0
a
0
0
i
идентична развернутой
цепочке столбиков
a
a
справа от
h
a
0
0
a
0
0
i
и в то же время идентич-
на развернутой последовательности
¯a
¯a
справа от
h
a
0
0
a
0
0
i
. Итак,
LM
n
(γ
2
) = {
x
0
x
0
a
0
0
a
0
0
h
w
w
i
| x ∈ U
∗
, mi(w) ∈ x t⊥ ¯x},
L
n
(γ
2
) = {x
0
a
0
0
w | x ∈ U
∗
, mi(w) ∈ x t⊥ ¯x},
где x
0
, ¯x — штрихованная и надчеркнутая копии буквы x ∈ U
∗
.
Следовательно, справа от
h
a
0
0
a
0
0
i
в обеих цепочках возникает
язык перетасованных копий над алфавитом U, а одновременно
с этим слева от
h
a
0
0
a
0
0
i
представлены (в штрихованной версии) те
строки, над которыми производилось тасование. (Поскольку
mi(U
∗
) = U
∗
, можно не учитывать операцию отражения.)
С помощью теоремы 3.17 отсюда можно извлечь представ-
ление рекурсивно перечислимых языков в качестве образов
языков из семейства ASL(n) при ОПМ-отображениях. В
разделе 4.5 этот результат будет усилен.
4.3 Выразительная сила систем со склейкой
В этом разделе мы изучаем соотношения между семействами
XSL(α) для различных X ∈ {A, O, R, S , SO, SR}, α ∈ {n, p, b},

168 4. Системы со склейкой
а также соотношения между ними и семействами из иерархии
Хомского.
Начнем с некоторых оценок сверху.
Теорема 4.1. OSL(n) ⊆ REG .
Доказательство. Рассмотрим одностороннюю систему γ =
(V, ρ, A, D). Обозначим через d длину самого длинного липкого
конца или самой длинной одинарной цепочки среди элементов
A или среди пар из D.
Построим контекстно свободную грамматику
G = (N, T, S, P ),
в которой
N = {h
u
λ
i
l
, h
u
λ
i
r
, h
λ
u
i
l
, h
λ
u
i
r
| u ∈ V
∗
, 0 6 |u| 6 d } ∪ {S},
T =
h
V
V
i
ρ
, а P содержит след ующие правил а:
1. S → h
u
1
u
2
i
l
h
x
1
x
2
i
h
v
1
v
2
i
r
для
u
1
u
2
h
x
1
x
2
i
v
1
v
2
∈ A, где
u
1
u
2
,
v
1
v
2
∈
λ
V
∗
∪
V
∗
λ
и
h
x
1
x
2
i
∈ WK
ρ
(V ).
2. h
u
1
u
2
i
l
→ h
u
0
1
u
0
2
i
l
h
w
1
w
2
i
, где
u
1
u
2
,
u
0
1
u
0
2
∈
λ
V
∗
∪
V
∗
λ
,
h
w
1
w
2
i
∈ WK
ρ
(V ) и существует пара из D вида
(
u
0
1
u
0
2
h
x
1
x
2
i
y
1
y
2
,
λ
λ
) с такими
y
1
y
2
∈
V
∗
λ
∪
λ
V
∗
и
h
x
1
x
2
i
∈ WK
ρ
(V ), что
h
x
1
y
1
u
1
x
2
y
2
u
2
i
=
h
w
1
w
2
i
.
(Применяя это правило, мы удлиняем цепочку влево так
же, как при использовании пары с пустым правым членом,
т. е. в соответст вии с ее левым липким концом. Клейкий
конец запоминается с помощью нетерминального символа
h
u
1
u
2
i
l
, в котором индекс l означает «левый». Отметим,
что
h
w
1
w
2
i
может равняться
h
λ
λ
i
.)

4.3. Выразительная сила систем со склейкой 169
3. h
u
1
u
2
i
r
→
h
w
1
w
2
i
h
u
0
1
u
0
2
i
r
, где
u
1
u
2
,
u
0
1
u
0
2
∈
λ
V
∗
∪
V
∗
λ
,
h
w
1
w
2
i
∈ WK
ρ
(V ) и существует пара из D вида
(
λ
λ
,
x
1
x
2
h
y
1
y
2
i
u
0
1
u
0
2
) с такими
x
1
x
2
∈
V
∗
λ
∪
λ
V
∗
и
h
y
1
y
2
i
∈ WK
ρ
(V ), что
h
u
1
x
1
y
1
u
2
x
2
y
2
i
=
h
w
1
w
2
i
.
(Аналогичная идея для случая удлинения вправо.)
4. h
λ
λ
i
l
→ λ, h
λ
λ
i
r
→ λ.
(Вывод завершается при отсутствии липких концов.)
Легко видеть, что L(G) = LM
n
(γ) = LM
d
(γ). В самом деле,
поскольку для построения цепочки используются только одно-
сторонние пары, операции, удл иняющие цепочку влево и впра-
во, не зависят друг от друга. Поэтому всегда можно применить
пару (
z
1
z
2
,
λ
λ
) или (
λ
λ
,
z
1
z
2
) из D так, что она прикле-
ится к растущей цепочке с помощью ограниченной склейки,
а значит, длина отростков на каждом шаге вывода не превы-
сит максимум длин отростков в элементах из A и из D. Итак,
нетерминальные символы из N управляют процессом вывода
так же, как это делают липкие концы.
В грамматике G нет выводов вида X =⇒
∗
uXv, где и u,
и v — непустые строки. Следовательно, язык L(G) регулярен,
см. [115]. Поскольку L(G) = LM
n
(γ) и L
n
(γ) есть образ LM
n
(γ)
при кодировании, имеем L
n
(γ) ∈ REG.
Следствие 4. 1. OSL(p) ⊆ REG.
Доказательство. Если в приведенном выше доказательстве
заменить число d из определения N на 2d (т. е. расширить воз-
можность запоминания липких концов в нетерминальных сим-
волах до удвоенного максимума длин липких концов элементов
из A и из D) и считать, что в посылках h
u
1
u
2
i
l
, h
u
1
u
2
i
r
пра-
вил групп 2 и 3 u
1
u
2
6= λ, получится такая грамматика G
0
, что
L(G
0
) = LM
p
(γ). Действительно, грамматика G
0
уже не может
удлинять последовательность в соответствующем направлении
после образования прямого конца, откуда L(G
0
) ⊆ LM
p
(γ). Об-
ратно, дл я каждого примитивного вычисления в γ легко стро-

170 4. Системы со склейкой
ится примитивное вычисление той же молекулы с задержкой
не более 2d. Такое вычисление можно промоделировать выво-
дом в G
0
, так как в силу примитивности не придется применять
те правила групп 2 и 3, которые мы исключили.
Из п ервого из примеров, указанных в разделе 4.2, вытекает
Теорема 4.2. Семейства SSL(n), SSL(p) содержат не кон-
текстно-свободные языки.
Следствие 4.2. Включения SOSL(α) ⊂ SSL(α), α ∈ {n, p},
являются строгими.
В случае двусторонних систем, даже простых, нельзя до-
биться ограниченности задержки по образцу доказательства
теоремы 4.1. Точнее, верен следующий результат.
Теорема 4.3. ASL(b) ⊆ LIN .
Доказательство. Рассмотрим систему γ = (V, ρ, A, D) общего
вида, и пусть L
d
(γ) = L
n
(γ) для некоторого целого числа d.
Построим линейную грамматику G = (N, T, S, P ), в которой
N = {h
u
1
u
2
,
v
1
v
2
i |
u
1
u
2
,
v
1
v
2
∈
λ
V
∗
∪
V
∗
λ
,
|u
1
|, |u
2
|, |v
1
|, |v
2
| 6 d} ∪ {S},
T =
h
V
V
i
ρ
, а P содержит след ующие правил а:
1. S →
h
w
1
w
2
i
h
u
1
u
2
,
v
1
v
2
i
h
z
1
z
2
i
, для
w
1
w
2
,
z
1
z
2
∈ WK
ρ
(V ),
h
u
1
u
2
,
v
1
v
2
i ∈ N
и (
w
1
w
2
u
1
u
2
,
v
1
v
2
z
1
z
2
) ∈ D.
(Выводы в G воспроизводят вычисления в γ, сделанные в
обратном порядке, т. е. от последней примененной пары из
D к «ц ентр у» последовательности, где используется аксио-
ма из A.)
