Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

3.1. Основные понятия 121

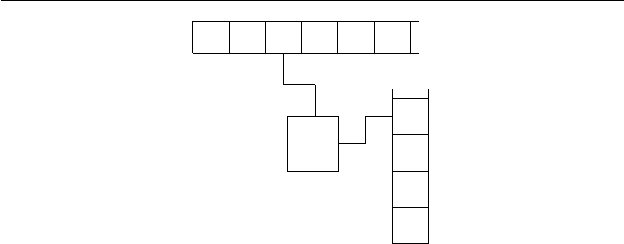
Рис. 3.3. Магазинный автомат.

Рефлексивное и транзитивное замыкание `

∗

отношения `

определяется обычным образом. Язык L(M ), распознаваемый

магазинным автоматом M, есть

{x ∈ V

∗

| (s

, x, Z

) `

∗

(s, λ, z) для некоторых s ∈ F, z ∈ U

∗

(Работа начинается в начальном состоянии s

при единствен-

ном символе Z

в магазине и заканчивается после просмотра

всей входной строки. При этом н ет ограничений на содержимое

магазина в конце работы.)

Магазинный автомат изображен на рис. 3.3, где показаны

входная лента, магазин, память и две головки: головка, скани-

рующая входную ленту, и читающая/пишущая головка, п осто-

янно позиционированная напротив верхней клетки магазина.

Недетерминированные магазинные автоматы распознают в

точности контекстно-свободные языки. У детерминированно-

го магазинного автомата поведение однозначно определяется

конфигурацией. Известно, что семейство языков, распознава-

емых детерминированными магазинными автоматами, строго

содержится в CF .

Машиной Тьюринга называется семерка

M = (K, V, T, B, s

, F, δ),

где K и V — непересекающиеся алфавиты (множество состоя-

ний и алфавит ленты), T ⊆ V — входной а лфав ит, B ∈ V −T —

символ пробела, s

∈ K — начальное состояние, F ⊆ K —

множество заключитель ных состояний, и δ — частичная функ-

122 3. Введение в теорию языков

ция из K × V в P(K × V × {L, R}) (функция переходов). Если

, b, d) ∈ δ(s, a) для s, s

∈ K, a, b ∈ V, и d ∈ {L, R}, то машина,

прочитав символ a в состоянии s, переходит в состояние s

, за-

меняя при этом a на b и сдвигая читающую/пишущую головку

влево, если d = L, и вправо, если d = R. Если card



δ(s, a)



6 1

для всех s ∈ K и a ∈ V , то говорят, что M детерминирована.

Мгновенным описа нием определенной выше машины Тью-

ринга называется строка xsy, где x ∈ V

∗

, y ∈ V

∗

(V −{B})∪{λ}

и s ∈ K. По нему однозначно устанавливается и содержимое

ленты, и сост ояние, и положение головки: она читает первый

символ строки y. Отметим, что символ пробела может появ-

ляться в x и в y, но не в последней позиции y. И x, и y могут

быть пустыми. Множество всех мгновенных описаний машины

M обозначается через ID

На множестве ID

определим отношение непосредствен-

ного следования `

таким образом:

xsay `

xbs

y, если и только если (s

, b, R) ∈ δ(s, a),

xs `

xbs,

если и только если (s

, b, R) ∈ δ(s, B),

xcsay `

cby, если и только если (s

, b, L) ∈ δ(s, a),

xcs `

cb, если и только если (s

, b, L) ∈ δ(s, B),

где x, y ∈ V

∗

, a, b, c ∈ V , s, s

∈ K.

Язык L(M), распознаваемый машиной Тьюринга M , есть

{w ∈ T

∗

| s

w `

∗

xsy для некоторых s ∈ F, x, y ∈ V

∗

(Это множество всех таких стро к, что машина, стартуя в на-

чальном состоянии с первого символа входной строки, достиг-

нет заключительного состояния.)

При другом подходе язык, принимаемый машиной Тью-

ринга, определяется как множество всех таких строк w ∈ T

∗

что машина, стартующая из конфигурации s

w, достигает та-

кой конфигурации, в которой дальнейшее движение невозмож-

но (иначе говоря, машина останавл ивается ). Эти два способа

определения языка L(M) эквивалентны и приводят к одному

и тому же семейству языков, а именно RE.

3.1. Основные понятия 123

Графическое представление машины Тьюринга такое же,

как у конечного автомата (рис. 3.1). Различие между ними про-

является только в процессе раб оты: головка машины Тьюрин-

га может перемещаться в обоих направлениях и переписывать

прочитанный символ (или стирать его, заменяя пробелом).

И детерминированные, и недетерминированные машины

Тьюринга характеризуют семейство рекурсивно перечислимых

языков.

Машину Тьюринга можно использовать для задания как

языков, так и отображений. Рассмотрим машину Тьюринга

M = (K, V, T, B, s

, F, δ). Если β = x

sax

∈ ID

и δ(s, a) = ∅,

т. е. в конфигурации β машина останавливается, мы пишем β ↓.

Определим отображение F

: ID

−→ P(ID

) правилом

(α) = {β ∈ ID

| α `

∗

β и β ↓}. Если машина M детерми-

нирована, то F

является отображением из ID

в ID

Говорят, что отображение f : U

∗

−→ U

∗

, где U

, U

— про-

извольные алфавиты, вычислимо на машине Тьюринга M, ес-

ли существуют рекурсивные отображения C и D (называемые

кодированием и декодированием),

C : U

∗

−→ ID

, D : ID

−→ U

∗

такие, что D





C(x)





= f(x).

В следующем разделе, обсуждая универсальные машины

Тьюринга, мы используем именно эту интерпретацию машин

Тьюринга (а также договоренность об окончании вычислений

по остановке, без использования заключительных состояний).

Работая с входной строкой, машина Тьюринга может ис-

пользовать настолько длинную ленту, насколько это необходи-

мо. Заметим, что конечные и магазинные автоматы используют

только те клетки ленты, в которых записана входная строка и

только в режиме чтения. В дополнение к этому, у магазинного

автомата есть неограниченная магазинная лента. Если рабочее

пространство на ленте, которое может использовать машина

Тьюринга, ограничено линейной функцией от длины входной

строки, то такая машина называется линейно ограниченным

автоматом. Эти машины характеризуют семейство CS.

124 3. Введение в теорию языков

Регулируемое переписывание. Выразительная сила кон-

текстно-свободных грамматик недостаточна для того, чтобы

покрыть многие важные синтаксические конструкции в есте-

ственных и искусственных языках, а контекстные граммати-

ки наоборот слишком сильны (так, для семейства CS многие

свойства оказываются неразрешимыми, и вывод в граммати-

ках, не являющихся контекстно-свободными, не может быть

описан в т ермина х деревьев). Поэтому заслуживает внимания

идея усилить выразительные возможности контекстно-свобод-

ных грамматик, контролируя применение их правил вывода.

Она п рив одит к рассмотрению регулируемых контекстно-сво-

бодных грамматик, несколько разнови дн остей которых будут

полезны для наших построений.

Контекстно-свободной матричной грамматикой назовем

четверку G = (N, T, S, M), где N и T — непересекающиеся

алфавиты нетерминальных и соответственно терминальных

символов, S ∈ N — аксиома, M — конечное множество матриц,

т. е. последовательностей вида (A

→ z

, . . . , A

→ z

), n > 1,

состоящих из контекстно-свободных правил в алфавите N ∪ T .

Действие элемента m = (r

, . . . , r

) на строку x состоит в по-

следовательном применении правил r

, . . . , r

в том порядке,

в котором они записаны. Получающаяся строка y называется

непосредственно выводимой из x, пишут x =⇒ y. Далее обыч-

ным образом определяется язык, порождаемый G. Семейство

языков, порождаемых контекстно-свободными матричными

грамматиками обозначается через MAT

(верхний индекс

показывает, что при выводе допустимы и λ-правила). Если ис-

пользуются только λ-свободные правила, то соответствующее

семейство обозначается через MAT.

Контекстно-свободной программируемой грамматикой на-

зовем четверку G = (N, T, S, M), где, как и в ыше, N, T и S

суть множества нетерминальных и терминальных символов и

начальный символ, а P — конечное множество продукций вида

(b : A → z, E, F ), где b — метка, A → z — контекстно-свободное

правило над N ∪ T , а E, F — два множества меток для продук-

ций из G. Множество E называют полем успеха, а множество

3.1. Основные понятия 125

F полем провала для соответствующей продукции. Продукция

из G применяется следующим образом: если контекстно-сво-

бодная часть может быть успешно выполнена, то она применя-

ется, а следующая выполняемая продукция выбирается среди

помеченных элементами из E, в противном случае, мы выби-

раем продукцию, помеченную каким-нибудь элементом из F , и

пытаемся применить ее. Программируемые грамматики такого

типа называются грамматиками с явной проверкой, если же у

продукций не задаются поля провала, то получается програм-

мируемая грамматика без явной проверки.

Иногда бывает полезно записывать прогр аммируемую

грамматику в виде G = (N, T, S, P, σ, ϕ), где N, T, S имеют

прежний смысл, P — множество обычных контекстно-свобод-

ных правил, а σ, ϕ суть отображения из P в P(P ); для правила

p ∈ P множество σ(p) — поле успеха (некоторое правило из

σ(p) должно использоваться после успешного применения пра-

вила p), а множество ϕ(p) — поле провала (некоторое правило

из ϕ (p) должно использоваться в случае, когда п рави ло p

неприменимо).

Контекстно-свободной упорядоченной грамматикой назо-

вем систему G = (N, T, S, P, >), где N, T , S имеют тот же

смысл, что и в предыдущих определениях, P — конечное мно-

жество контекстно-свободных продукций, а > — частичный

порядок на P . Продукцию p можно применить к сентенциаль-

ной форме x только в том случае, когда она применима к x

как контекстно-свободное правило и никакая продукция r ∈ P

со свойством r > p не применима к x.

Контроль над примен ением правил вывода может основы-

ваться и на проверке контекстных условий.

Обобщенной полукондициональной грамматикой назовем

четверку G = (N, T, S, P ), в которой N, T , S имеют тот же

смысл, что и в предыдущих определениях, P — конечное

множество тр оек вида p = (A → w; E, F ), где A → w — кон-

текстно-свободная продукция над N ∪ T , а E, F — конечные

подмножества в (N ∪ T )

. Правило p применимо к строке

x ∈ (N ∪ T )

∗

, содержащей подстроку A, только при условии,

126 3. Введение в теорию языков

что каждый элемент из E также является подстрокой в x,

а ни один элемент из F подстрокой в x не является. (Если

какое-то из множеств E и F пусто, то нет и соответствующего

ограничения.) При этом E называют множеством разреша-

ющих контекстн ых условий тройки p, а F — множеством

запрещающих контекстных условий.

Если card(E) 6 1 и card(F ) 6 1 для всех p ∈ P , то

G = (N, T, S, P ) называется полукондициональной граммати-

кой. Если E, F ⊆ N, то говорят, что грамматика случайно

контекстная.

Два других хорошо известных типа грамматик с контекст-

ными условиями — это кондициональные и слабо кондициональ-

ные грамматики. Кондициональная грамматика — это четверка

G = (N, T, S, P ), в которой P — конечное множество продук-

ций вида p = (A → w; R

), где R

— р егулярный язык над

N ∪ T . Правило p можно применить к строке x, содержащей

подстроку A, только при условии, что x ∈ R

. Если имеется

такой регулярный язык R, что R = R

для каждого p ∈ P , то

говорят о слабо кондициональной грамматике.

Кондициональные, слабо кондициональные и полукондици-

ональные грамматики обладают одинаковой порождающей си-

лой. Они порождают либо все рекурсивно перечислимые, либо

все контекстные языки в зависимости от того, разрешается ли

использовать λ-правила.

Наконец, рассмотрим понятие простой матричной грам-

матики. Такая грамматика (степени n > 1) представляет собой

систему G = (N

, . . . , N

, T, S, M), в которой N

, . . . , N

, T —

попарно непересекающиеся алфавиты, S /∈ T ∪

i=1

, а M —

множество матриц следующего вида:

(S → w

. . . w

), w

∈ (T ∪ N

)

∗

, 1 6 i 6 n,

причем |w

= |w

, 1 6 i, j 6 n;

→ w

, . . . , A

→ w

), A

∈ N

, w

∈ (T ∪ N

)

∗

, 1 6 i 6 n,

причем |w

= |w

, 1 6 i, j 6 n.

3.1. Основные понятия 127

При этом для каждой матрицы из M рассматрива ется левосто-

ронний вывод (каждое правило A

→ w

применяется к край-

нему слева вхождению символа из N

в данную строку).

Простые матричные грамматики порождают семейство по-

лулинейных языков, лежащее строго между CF и CS.

Идея контроля над применением контекстно-свободных

правил с целью повышения порождающей силы контекстно-

свободных грамматик будет полезна в дальнейшем.

Грамматические системы. Еще один весьма плодотворный

подход к повышению порождающей силы контекстно свобод-

ных (а в определенных случаях, и регулярных) грамматик)

состоит в рассмотрении распределенных порождающих уст-

ройств, т. е. агрегатов, собранных из нескольких грамматик,

работающих вместе в соответствии с точно определенным

протоколом. Это приводит к идее грамматических систем.

Исследовались два основных класса таких систем: последо-

вательные (введенные в [50] под названием кооперирующиеся

распределенные системы) и параллельные взаимодействующие

системы, введенные в [263]. Для дальнейшего полезнее второй

класс, поэтому мы приведем только его определение.

Параллельная взаимодействующая система степени n,

n > 1, — это а грегат

Γ =



N, T, K, (S

, P

), . . . , (S

, P

)



в котором N, T , K — попарно непересекающиеся алфавиты,

K = {Q

, . . . , Q

}, S

∈ N, P

— конечные множества перепи -

сывающих правил над N ∪ T ∪ K, 1 6 i 6 n. Элементы N и T

называются соответственно нетерминальными и терминаль-

ными символами, а элементы K — символами запроса. Пары

, P

) — это компоненты системы (часто компонентами назы-

вают и множества P

). Заметим, что символы запроса взаимно

однозначно соответствуют компонентам и что когда речь идет

о типе компонент как грамматик Хомского, то символы запро-

са рассматриваются как нетерминальные.

Назовем конфигура цией произвольную n-ку (x

, . . . , x

где x

∈ (N ∪ T ∪ K)

∗

, 1 6 i 6 n. Пусть (x

, . . . , x

) и

128 3. Введение в теорию языков

, . . . , y

) — две таких конфигурации, п рич ем x

/∈ T

∗

. Мы

пишем (x

, . . . , x

) =⇒

, . . . , y

), если выполняется одно из

двух следующих условий.

(i) Если |x

= 0 для всех 1 6 i 6 n, то либо x

=⇒

, либо

= y

∈ T

∗

, 1 6 i 6 n .

(ii) Если |x

> 0 для некоторого i, 1 6 i 6 n, то представим

эту строку x

как

= z

. . . z

t+1

где t > 1, z

∈ (N ∪ T )

∗

, 1 6 j 6 t + 1. Каждый символ Q

трактуется как запрос о координате x

текущей конфигу-

рации (x

, . . . , x

). Е сли |x

= 0 для всех 1 6 j 6 t, то

полагаем

= z

. . . z

t+1

[и y

= S

для всех 1 6 j 6 t], иначе y

= x

. Для всех

прочих индексов j полагаем y

= x

Пункт (i) определяет шаг переписывания. Переписывание

происходит покоординатно, синхронно и использует по одному

правилу из каждой компоненты, которой соответствует нетер-

минальная строка. Пункт (ii) определяет шаг взаимодействия,

состоящий в том, что в строке x

все символы запроса Q

за-

меняются на соответствующие им строки x

при условии, что

сами эти строки не содержат символов запр оса. Взаимодей-

ствие имеет приоритет перед переписыванием, т. е. переписыва-

ние разрешено лишь тогда, когда во всей текущей конфигура-

ции нет символов запроса. Работа системы блокируется как при

«зацикливании» запросов, так и в случае, когда запросов нет,

но правило (i) неприменимо, поскольку некоторая компонен-

та не может переписать соответствующую ей сентенциальную

форму, хотя последняя еще является нетерминальной строкой.

Определенное выше отношение =⇒

выполняется в воз-

вратном режиме: после взаимодействия каждая компонента, к

которой посылался запрос, возобновляет работу со своей акси-

омы. Если в приведенном определении опустить часть, взятую

в квадратные скобки [и y

= S

для всех 1 6 i 6 t], то п о-

лучится невозвратный режим вывода: после взаимодействия

3.1. Основные понятия 129

компоненты, к которым посылались запросы, продолжают об-

работку текущих строк. Получаемое таким образом отношение

обозначается через =⇒

Язык, порожденный системой Γ, есть по определению язык,

порожденный ее первой компонентой при условии, что процесс

вывода начинается с конфигурации (S

, . . . , S

(Γ) = {w ∈ T

∗

| (S

, . . . , S

) =⇒

∗

(w, α

, . . . , α

где α

∈ (N ∪ T ∪ K)

∗

, 2 6 i 6 n}, f ∈ {r, nr}.

Тем самым, значения координат 2, . . . , n в заключительной кон-

фигурации вывода не принимаются во внимание; более того,

предполагается, что система Γ останавливается, как только

первая компонента выведет терминальную строку.

Описанные системы взаимодействуют по запросу. Класс па-

раллельных грамматических систем, взаимодействующих по

приказу, рассмотрен в [55]. В таких системах с каждой ком-

понентой ассоциирован н екоторый регулярный язык. На каж-

дом шаге компонента посылает свою текущую сентенциальную

форму всем прочим компонентам, но посланная строка п ри ни-

мается, только при условии, что она принадлежит регулярному

языку, ассоциированному с компонентой-получателем. Так им

образом, регулярные языки д ействуют как фильтры, контро-

лируя взаимодействие методом, сходным со спо собом контроля

за выводом в кондициональных грамматиках.

Здесь мы дадим формальное описание только одного специ-

ального класса таких систем. Мы рассмотрим системы, рабо-

тающие с максимальными выводами в качестве шагов перепи-

сывания, взаимодействующие без расщепления строк, заменя-

ющие строку принимающей компоненты произведением полу-

ченных сообщений в порядке, соответствующем порядку ком-

понент, и возвращающиеся к аксиомам после взаимодействия.

Порожденным языком будет считаться язык первой компонен-

ты — хозяина системы. Фильтрами будут регулярные языки.

Итак, мы имеем агрегат

Γ =



N, T, (S

, P

, R

), . . . , (S

, P

, R

)



130 3. Введение в теорию языков

в котором N и T — непересекающиеся алфавиты (нетерминаль-

ный и терминальный), S

∈ N, P

— конечные множества кон-

текстно-свободных правил над N ∪ T , R

— регулярные языки

над N ∪ T , 1 6 i 6 n.

Шаг переписывания для системы Γ определим так:

, . . . , x

) =⇒ (y

, . . . , y

) тогда и только тогда, когда

=⇒

∗

в P

и нет такого z

∈ (N ∪ T )

∗

что y

=⇒ z

в P

Шаг взаимодействия, обозначаемый через

, . . . , x

) ` (y

, . . . , y

)

определим следующим образом. Пусть

, j) =

(

λ, если x

/∈ R

или i = j,

, если x

∈ R

и i 6= j,

где 1 6 i, j 6 n,

∆(j) = δ(x

, j)δ(x

, j) · · · δ(x

, j), где 1 6 j 6 n,

(«сводное сообщение», принимаемое j-й компонентой), и

δ(i) = δ(x

, 1)δ(x

, 2) · · · δ(x

, n), где 1 6 ı 6 n,

(«сводное сообщение», посылаемое i-й компонентой, т. е. сте-

пень строки x

, показатель которой равен числу адресатов это-

го сообщения). Далее, для 1 6 i 6 n оп редел им











∆(i), если ∆(i) 6= λ,

, если ∆(i) = λ и δ(i) = λ,

, если ∆(i) = λ и δ(i) 6= λ.

Таким образом, y

есть либо произведение полученных сообще-

ний, если таковые имеются, либо предыдущая строка, если i-я

компонента не участвует во взаимодействии, либо S

, если i-я

компонента посылает, но не получает сообщения. Отметим, что

компонента не может посылать сообщение самой себе.

Порожденный язык определяется следующим образом:

L(Γ) = {w ∈ T

∗

| (S

, . . . , S

) =⇒ (x

(1)

, . . . , x

(1)

) ` (y

(1)

, . . . , y

(1)

)