Патудин В.М., Блем А.Г. Математическая экономика
Подождите немного. Документ загружается.


81
5.4. Задача замены оборудования как задача динамического про-
граммирования
В общем виде проблема ставится следующим образом: определить оп-
тимальную стратегию использования оборудования в период времени дли-
тельностью
m
лет, причем прибыль за каждые
i
лет,
mi ,1=
от использования
оборудования возраста
t
лет должна быть максимальной.
Известны:
)(tr
– выручка от реализации продукции, произведенной за
год на оборудовании возраста
t
лет,
)(tl
– годовые затраты, зависящие от воз-
раста оборудования
t
,
)(tc
– остаточная стоимость оборудования возраста
t
лет,
P
– стоимость нового оборудования. Под возрастом оборудования пони-
мается период эксплуатации оборудования после последней замены, выражен-
ный в годах.
Для построения математической модели последовательно выполняют-
ся этапы, сформулированные ниже.
1. Определение числа шагов. Число шагов равно числу лет, в течение
которых эксплуатируется оборудование.
2. Определение состояний системы. Состояние системы характеризу-
ется возрастом оборудования
t
;
mt ,0=
.
3. Определение управлений. В начале
i
-го шага,
mi ,1=
может быть
выбрано одно из двух управлений: заменять или не заменять
оборудование. Каждому варианту управления приписывается
число
=
заменяетсяиеоборудованесли
заменяетсянеиеоборудованесли
x
i
,1
,0
(5.4.1)
4. Определение функции выигрыша на
i
-м шаге. Функция выигрыша
на
i
-м шаге – это прибыль от использования оборудования к концу
i
-го года
эксплуатации,
mt ,0=
,
mi ,1=
.
−+−
−−
=
заменяетсяиеоборудованеслиlrptc
заменяетсянегодагоiначалевиеоборудованеслиtltr
i
),0()0()(
),()(
ϕ
(5.4.2)
Таким образом, если оборудование не продается, то прибыль от его
использования – это разность между стоимостью произведенной продукции и
эксплуатационными издержками. При замене оборудования прибыль состав-
ляет разность между остаточной стоимостью оборудования и стоимостью но-
вого оборудования, к которой прибавляется разность между стоимостью про-
дукции и эксплуатационными издержками для нового оборудования, возраст
которого в начале
i
-го шага составляет 0 лет.
5. Определение функции изменения состояния.
=
=+
=
1,1
0,1
)(
i
i
i
xесли
xеслиt
tf
(5.4.3)
6. Составление функционального уравнения для i=m.
−+−
−
=
∈
)()0()(
)()(
max)(
}1,0{
tlrptc
tltr
tW
m
x
m
(5.4.4)

82
7. Составление основного функционального уравнения
+−+−
++−
=
+
+
∈
)1()0()0()()(
)1()()(
max)(
1
1
}1,0{
i
i
x
m
Wlrtptc
tWtltr
tW
i
(6.4.5)
где
)(tW
i
— прибыль от использования оборудования возраста t лет с
i
-
го шага (с конца
i
-го года) до конца периода эксплуатации.
)1(
1
+
+
tW
i
— прибыль от использования оборудования возраст а
1
+
t
год
с (
1
+
i
)-го шага до конца периода эксплуатации;
Таким образом, математическая модель задачи построена.
Расчет модели проведем для конкретного примера.
Пример 5.4.1
m
=12,
p
=10,
)(tc
=0,
)()()( ttltr
ϕ
=
−
Значения
)(t
ϕ
заданы в табл. 5.4.1
Таблица 5.4.1
Для данного примера функциональные уравнения будут иметь вид
+−
=
∈
)0(
)(
max)(
}1,0{
ϕ
ϕ
p
t
tW
m
x
m
;
++−
++
=
+
+
∈
)1()0(
)1()(
max)(
1
1
}1,0{
i
i
x
m
Wp
tWt
tW
m
ϕ
ϕ
Для решения данной задачи заполняется табл. 5.4.2.
Таблица 5.4.2
В левой колонке таблицы записываются возможные состояния систе-
мы
12,0=t
, в верхней строке – номера шагов
12,0=i
. Для каждого шага опре-
деляются условные оптимальные управления
)(tx
i
и условный оптимальный
выигрыш
)(tW
i
с
i
-го шага и до конца для оборудования возраста
t
лет.

83
Поясним, как заполняется таблица для нескольких шагов.
1. Условная оптимизация начинается с последнего 12-го шага. Для
i
=12
рассматриваются возможные состояния системы
12,0=t
. Функциональ-
ное уравнение на 12-м шаге имеет вид
+−
+
=
∈
)0(
)1)((
max)(
}1,0{
12
ϕ
ϕ
p
tt
tW
x
1)t=0
0)0(;10
1010
10
max)0(
12
1,0
12
==
+−
= xW
2)t=1
0)1(;9
1010
9
max)1(
12
1,0
12
==
+−
= xW
………………..
10)t=9
0)9(;1
1010
1
max)9(
12
1,0
12
==
+−
= xW
11)t=10
1)10(;0
1010
0
max)10(
12
1,0
12
==
+−
= xW
…………………
13)t=13
1)12(;0
1010
0
max)12(
12
1,0
12
==
+−
= xW
Таким образом, на 12-м шаге оборудование возраста 0 — 9 лет заме-
нять не надо. Оборудование возраста 10—12 лет можно заменить или продол-
жить его эксплуатацию, так как для t=10, 11, 12 имеется два условных опти-
мальных управления 1 и 0.
По результатам расчетов заполняются два столбца таблицы, соответст-
вующие
i
=12.
2. Условная оптимизация 11-го шага.
Для
i
=11 рассматриваются все возможные состояния системы
t=0,1,2,...,12.Функциональное уравнение на 11-м шаге имеет вид
++−
++
=
)1()0(
)1()(
max)(
12
12
0,1
11
Wp
tWt
tW
ϕ
ϕ
i
=11
1)t=0
0)0(;19
91010
910
max
)1()0(
)1()0(
max)0(
11
0,1
12
12
0,1
11
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
2)t=2
0)1(;17
91010
89
max
)1()0(
)2()1(
max)1(
11
0,1
12
12
0,1
11
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
……………………………

84
6)t=5
1)5(;9
91010
45
max
)1()0(
)6()5(
max)5(
11
0,1
12
12
0,1
11
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
7)t=6
1)6(;9
91010
34
max
)1()0(
)7()6(
max)6(
11
0,1
12
12
0,1
11
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
…………………………..
13)t=12
1)12(;9
91010
0
max
)1()0(
)12(
max)12(
11
0,1
12
0,1
11
==
++−
=
++−
= x
Wp
W
ϕ
ϕ
Таким образом, на 11-м шаге не следует заменять оборудование воз-
раста 0—4 года. Для оборудования возраста 5 лет возможны две стратегии ис-
пользования: заменить или продолжать эксплуатировать.
Начиная с 6-го года оборудование следует заменять. По результатам
расчетов заполняются два столбца таблицы, соответствующие
i
=11,
i
=10
1)t=0
0)0(;27
171010
1710
max
)1()0(
)1()0(
max)0(
10
0,1
11
11
0,1
10
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
2)t=1
0)1(;24
171010
159
max
)1()0(
)2()1(
max)1(
10
0,1
11
11
0,1
10
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
3)t=2
0)2(;21
171010
138
max
)1()0(
)3()2(
max)2(
10
0,1
11
11
0,1
10
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
4)t=3
0)3(;18
171010
117
max
)1()0(
)4()3(
max)3(
10
0,1
11
11
0,1
10
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
5)t=4
0)4(;17
171010
96
max
)1()0(
)5()4(
max)4(
10
0,1
11
11
0,1
10
==
++−
+
=
++−
+
= x
Wp
W
W
ϕ
ϕ
……………………………
13)t=12
1)12(;17
171010
0
max
)1()0(
)12(
max)12(
10
0,1
12
0,1
10
==
++−
=
++−
= x
Wp
W
ϕ
ϕ
На 10-м шаге не следует заменять оборудование возраста 0-3 года. На-
чиная с 4-го года оборудование следует заменять, так как новое оборудование
приносит большую прибыль.
По результатам расчетов заполняются два столбца, соответствующие
i
=10.
Аналогичным образом заполняются остальные девять столбцов табли-
цы. При расчетах
)(
1
tW
i+
на каждом шаге значения
)(t
ϕ
для каждого
12,0=t
бе-

85
рутся из таблицы исходных данных, приведенной в уcловии задачи, а значения
)(tW
i
– из последнего, заполненного на предыдущем шаге столбца.
Этап условной оптимизации заканчивается после заполнения табл.
5.4.2.
Безусловная оптимизация начинается с первого шага.
Предположим, что на первом шаге
i
=1 имеется новое оборудование,
возраст которого 0 лет.
Для
0
1
== tt
оптимальный выигрыш составляет
)0(
1
W
=82. Это значение
соответствует максимальной прибыли от использования нового оборудования
в течение 12 лет.
82)0(*
1
== WW
Выигрышу
)0(
1
W
=82 соответствует безусловное оптимальное управле-
ние
0)0(
1
=x
.
Для
i
=2 по формуле (5.4.3)
11
12
=+= tt
.
Безусловное оптимальное управление
0)1(
2
=x
.
Для
i
=3
21
23
=+= tt
.
Безусловное оптимальное управление
0)2(
3
=x
.
И далее соответственно
12
11
10
9
8
7
6
5
4
=
=
=
=
=
=
=
=
=
i
i
i
i
i
i
i
i
i
31
21
1
41
31
21
1
41
31
1112
1011
10
89
78
67
6
45
34
=+=
=+=
=
=+=
=+=
=+=
=
=+=
=
+
=
tt
tt
t
tt
tt
tt
t
tt
tt
0)3(
0)2(
0)1(
1)4(
0)3(
0)2(
0)1(
1)4(
0)3(
12
11
10
9
8
7
6
5
4
=
=
=
=
=
=
=
=
=
x
x
x
x
x
x
x
x
x
Управления, составляющие оптимальную стратегию использования
оборудования, выделены в табл. 5.4.2 жирным шрифтом.
В рамках данной задачи оптимальная стратегия заключается в замене
оборудования при достижении им возраста 4-х лет. Аналогичным образом
можно определить оптимальную стратегию использования оборудования лю-
бого возраста. Предлагаем читателю самостоятельно в этом убедиться.
5.5. Оптимальное распределение инвестиций как задача динамиче-
ского программирования
Инвестор выделяет средства в размере
D
условных единиц, которые
должны быть распределены между
m
-предприятиями. Каждое
i
-е предпри-
ятие при инвестировании в него средств
x
приносит прибыль
)(x
i
ϕ
усл. ед.,
mi ,1=
. Нужно выбрать оптимальное распределение инвестиций между пред-
приятиями, обеспечивающее максимальную прибыль.

86
Выигрышем W данной задаче является прибыль, приносимая
m
-
предприятиями.
Построение математической модели.
1. Определение числа шагов. Число шагов т равно числу предпри-
ятий, в которые осуществляется инвестирование.
2. Определение состояний системы. Состояние системы на каждом
шаге характеризуется количеством средств
s
, имеющихся в наличии перед
данным шагом,
Ds
≤
.
3. Выбор шаговых управлений. Управлением на
i
-м шаге
i
x
,
mi ,1=
яв-
ляется количество средств, инвестируемых в
i
-е предприятие.
4. Функция выигрыша на
i
-м шаге
)(x
i
ϕ
(5.5.1)
— это прибыль, которую приносит
i
-е предприятие при инвестирова-
нии в него средств
i
x
.
∑
=
=
m
i
ii
xW
1
ϕ
,
следовательно, данная задача может быть решена методом динамиче-
ского программирования.
5. Определение функции перехода в новое состояние.
xsxsf
i
−=),(
(5.5.2)
Таким образом, если на
i
-м шаге система находилась в состоянии s, а
выбрано управление х, то на
1
+
i
-м шаге система будет находиться в состоя-
нии
x
s
−
. Другими словами, если в наличии имеются средства в размере s усл.
ед., и в
i
-е предприятие инвестируется х усл. ед., то для дальнейшего инвести-
рования остается
x
s
−
усл. ед.
6. Составление функционального уравнения для i=m.
)()( ssW
mm
ϕ
=
, (5.5.3)
ssx
m
=)(
(5.5.4)
На последнем шаге, т.е. перед инвестированием средств в последнее
предприятие, условное оптимальное управление соответствует количеству
средств, имеющихся в наличии; т.е. сколько средств осталось, столько и надо
вложить в последнее предприятие. Условный оптимальный выигрыш равен
доходу, приносимому последним предприятием.
7. Составление основного функционального уравнения. Подставив в
формулу (5.2.4) выражения (5.5.1) и (5.5.2), получаем следующее функцио-
нальное уравнение
)}()({)(
1
max
xsWxsW
ii
sx
i
−+=
+
≤
ϕ
(5.5.5)
Поясним данное уравнение. Пусть перед
i
-м шагом у инвестора оста-
лись средства в размере s ycл. ед. Тогда х усл. ед. он может вложить в
i
-e
предприятие, при этом оно принесет доход
)(x
i
ϕ
, а оставшиеся
x
s
−
усл. ед.– в
остальные предприятия с
1
+
i
-го до т-го. Условный оптимальный выигрыш от
87
такого вложения
)(
1
xsW
i
−
+
. Оптимальным будет то условное управление х, при
котором сумма
)(x
i
ϕ
и
)(
1
xsW
i
−
+
максимальна.
Проведем численный расчет модели.
Пример 5.5.1
D=5000, m=3.
Значение
)(x
i
ϕ
,
3,1=i
заданы в табл. 5.5.1
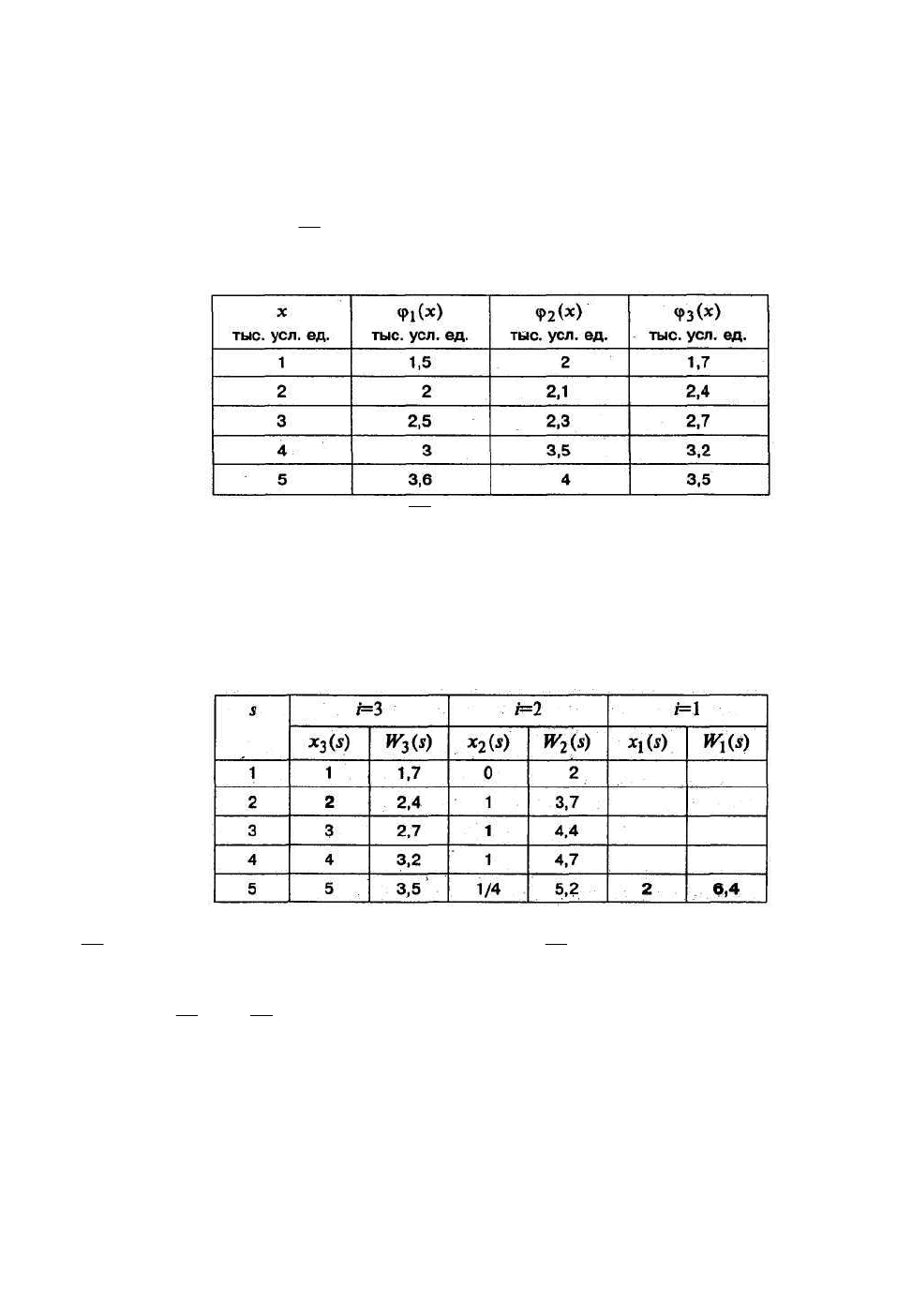
Таблица 5.5.1
Для
21
xx >
,
)()(
21
xx
ii
ϕϕ
≥
,
5,1=i
Для простоты в задаче сделано предположение, что вкладываются
только тысячи условных единиц.
Проведем условную оптимизацию. По ее результатам заполняется
табл. 5.5.2.
Таблица 5.5.2
В первой колонке таблицы записываются возможные состояния систе-
мы
5,1=s
, в верхней строке – номера шагов
3,1=i
. На каждом шаге определя-
ются условные оптимальные управления
)(sx
i
и условные оптимальные выиг-
рыши
)(sW
i
,
3,1=i
,
5,1=s
.
1. Проведение условной оптимизации для последнего шага
i
=3.
Функциональное уравнение на последнем шаге имеет вид
)3()(
33
ϕ
=sW
,
ssx =)(
3
,
поэтому два столбца табл. 6.5.2, соответствующие
i
=3, заполняются
автоматически по таблице исходных данных.
2. Условная оптимизация для
i
=2.
Функциональное уравнение
)}()({)(
322
max
xsWxsW
sx
−+=
≤
ϕ
.
88
Для проведения условной оптимизации заполним ряд вспомогательных
таблиц (табл. 5.5.3–5.5.8), соответствующих различным значениям s, т.е. раз-
личным исходам окончания предыдущего шага.
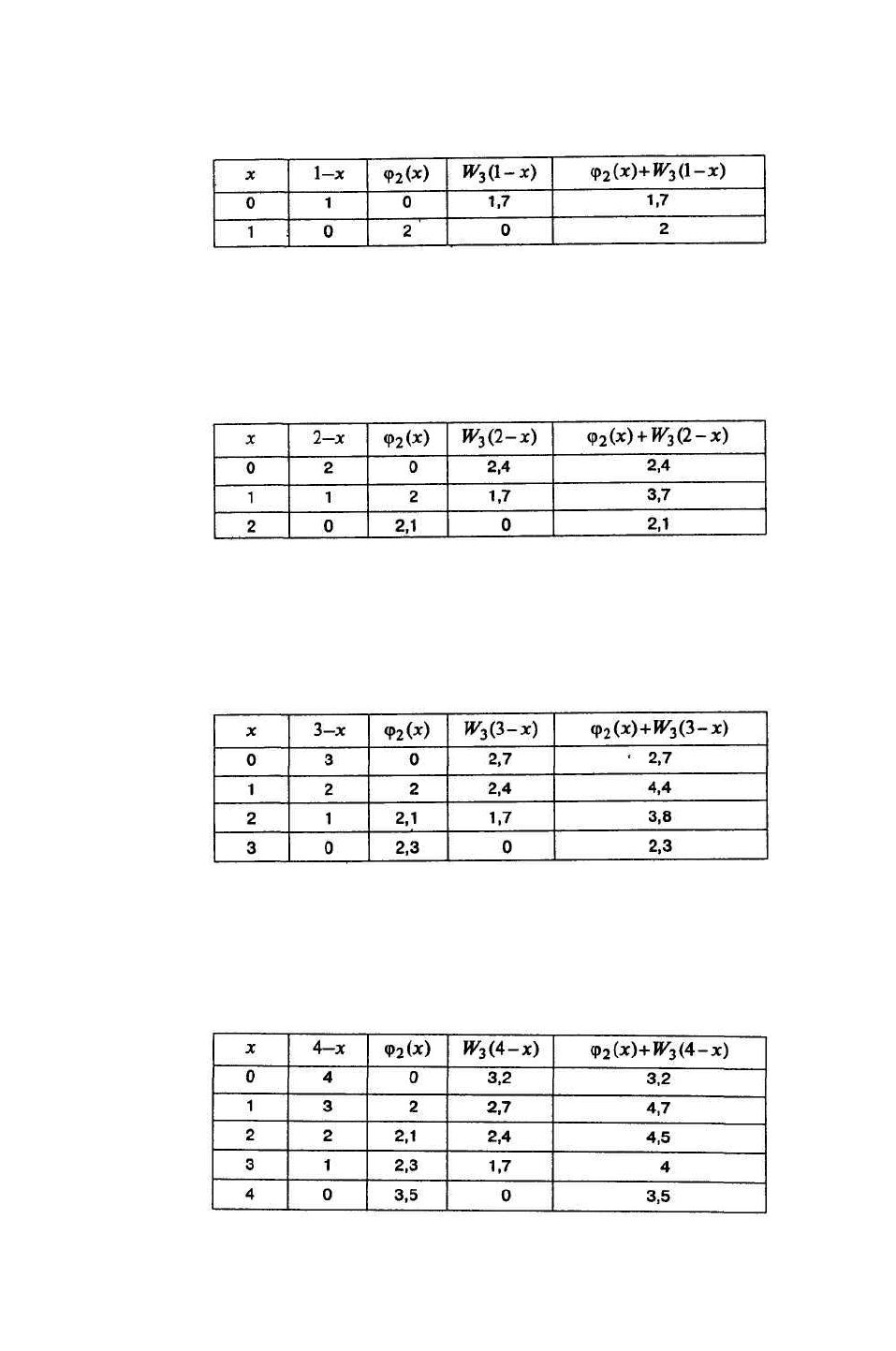
1)s=l
Таблица 5.5.3
2}2;7,1{max
1
=
≤x
, следовательно
2)1(
2
=W
1)1(
2
=x
2)s=2
Таблица 5.5.4
7,3}1,2;7,3;4,2{max
2
=
≤x
, следовательно
7,3)2(
2
=W
1)2(
2
=x
3)s=3
Таблица 5.5.5
4,4}3,2;8,3;4,4;7,2{max
3
=
≤x
4,4)3(
2
=W
1)3(
2
=x
4)s=4
Таблица 5.5.6
7,4}5,3;4;5,4;7,4;2,3{max
4
=
≤x
7,4)4(
2
=W
1)4(
2
=x
89
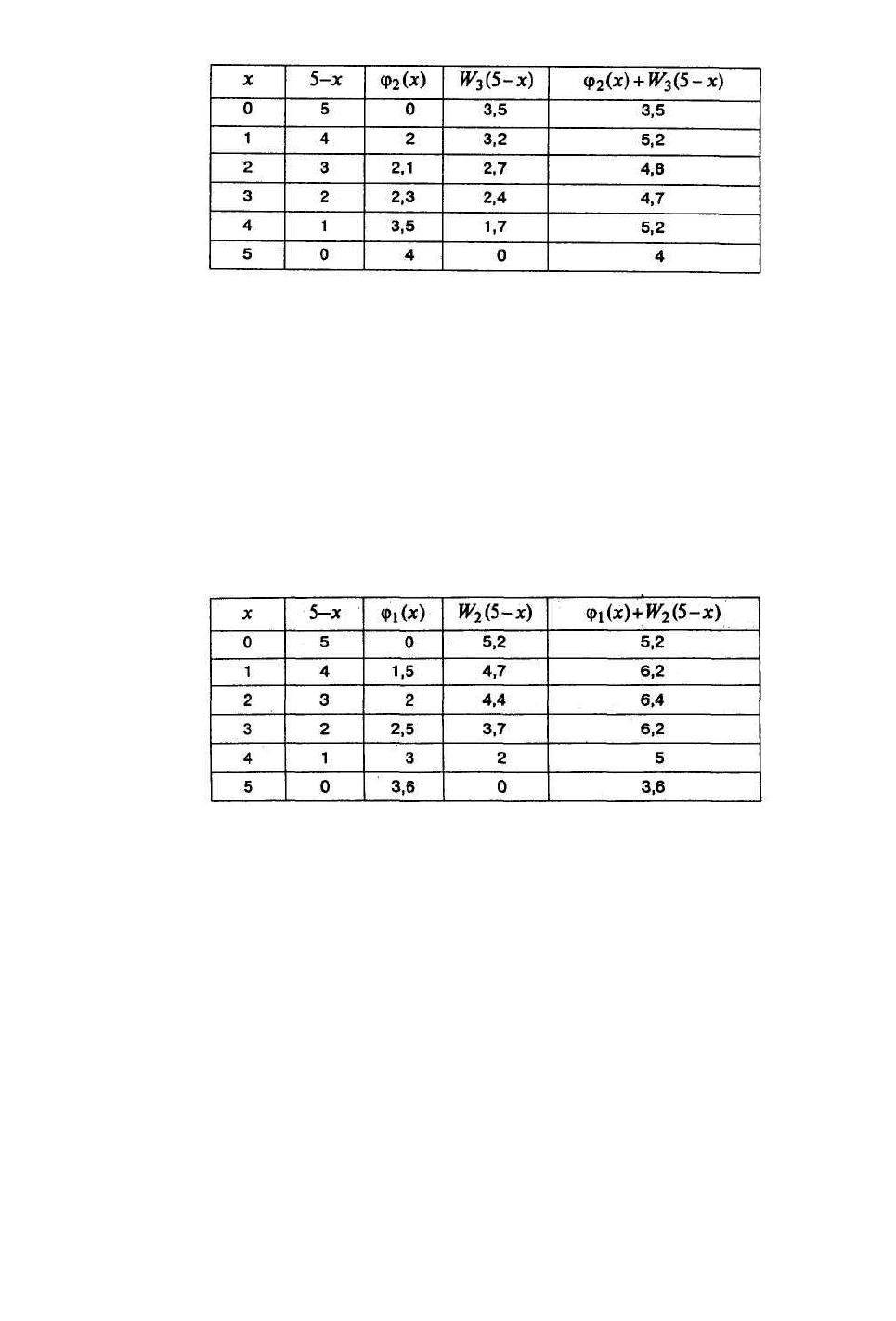
5)s=5
Таблица 5.5.7
2,5}4;2,5;8,4;2,5;5,3{max
5
=
≤x
Для s=5
2,5)5(
2
=W
возможны два условных оптимальных управления
1)5(
2
=x
и
4)5(
2
=x
3. Условная оптимизация для
i
=l.
Перед первым шагом состояние системы известно.
s=D=5 тыс. усл. ед., и условную оптимизацию следует проводить толь-
ко для этого значения
s=5
Таблица 5.5.8
4,6}6,3;5;2,6;4,6;2,6;2,5{max
5
=
≤x
, следовательно,
4,6)5(
2
=W
2)5(
1
=x
Оптимальная прибыль, приносимая тремя предприятиями при инве-
стировании в них 5 тыс. усл. ед., равна 6,4 тыс. усл. ед.
Проведем безусловную оптимизацию.
Ее результаты отмечены в таблице.
1
=
i
5
1
=s
4,6)5(
1
=W
;
2)5(*
11
== xx
.
Для
2
=
i
по формуле (6.5.2)
325
112
=−=−= xss
.
4,4)3(
2
=W
;
1)3(*
22
== xx
.
Для
3
=
i
213
223
=−=−= xss
.
4,2)2(
3
=W
;
2)2(*
33
== xx
.
)2;1;2(*
=
x
Таким образом, для получения максимальной прибыли в размере 6400
усл. ед. следует по 2000 усл. ед. вложить в первое и третье предприятия и 1000
усл. ед. – во второе предприятие.

90
Следует понимать, что полученное решение есть лишь некоторое при-
ближение к оптимальному решению. Его можно улучшить, т.е. приблизить к
оптимальному, взяв более мелкий шаг оптимизации, например вкладывать в
предприятия средства, кратные 500 усл. ед. В заключение следует отметить,
что после построения математической модели динамического программирова-
ния, т.е. выполнения этапов 1–7 пункта 6.2, для расчета модели может быть со-
ставлена программа. Использование компьютера позволит решить задачу
большой размерности, т.е. получить решение, достаточно близкое к оптималь-
ному.
После изучения данного раздела следует выполнить контрольную ра-
боту № 5
