Патудин В.М., Блем А.Г. Математическая экономика

Подождите немного. Документ загружается.

у*. При этом соответствующие им оптимальные значения целевых функций

*)(* xff

*)(* ygg

равны.

Поясним экономический смысл двойственной модели.

Пусть в качестве управляющих переменных

njx

,1, =

исходной модели

рассматривается число изделий, производимых некоторым предприятием, а

параметрами

mib

,1, =

– количество ресурсов

-го типа, используемых для из-

готовления изделий. Через

njmia

,1,,1, ==

обозначено количество ресурсов

го типа, идущее на изготовление одного изделия

-го вида, (

– прибыль от

реализации одного изделия

-го вида). Тогда исходная модель (2.7.1), (2.7.2)

соответствует задаче определения оптимального плана производства продук-

ции, обеспечивающего максимальную прибыль.

Пусть предприятие решило прекратить производство изделий и про-

дать ресурсы, идущие на их изготовление. Обозначим через

цены на еди-

ницу ресурсов

-го вида,

mi ,1=

. Цены на ресурсы должны удовлетворять сле-

дующим двум условиям: во-первых, они не должны быть слишком высокими,

иначе ресурсы невозможно будет продать; а во-вторых, цены на ресурсы

должны быть такими, чтобы прибыль от их реализации была больше прибыли

от реализации готовой продукции. Первое условие выражается формулой

(2.7.3), второе условие – ограничениями (2.7.4). В левой части каждого из не-

равенств (2.7.4) стоит прибыль от продажи ресурсов всех типов, идущих на

изготовление

-го изделия, в правой части – прибыль от продажи

-го изде-

лия,

nj ,1=

. Таким образом, двойственная задача (2.7.3) – (2.7.4) соответствует

следующей экономической проблеме: по каким минимальным ценам следует

продавать ресурсы, чтобы прибыль от их реализации была больше прибыли,

полученной от реализации продукции, изготавливаемой с использованием

этих ресурсов. Значения переменных

yyy ,...,,

часто называют теневыми

ценами.

Построение двойственной задачи позволяет глубже разобраться в по-

ставленной экономической проблеме.

2.8. Целочисленное линейное программирование. Метод Гомо-

ри

Если управляющие переменные в задаче линейного программирования

определяют количество единиц неделимой продукции, то оптимальное реше-

ние должно быть получено в целых числах. К задачам такого типа относится

большое число экономических задач, например распределение производст-

венных заказов между предприятиями, оптимальный раскрой материалов, оп-

ределение загрузки оборудования, распределение транспортных средств по

рейсам, задачи производства и реализации неделимой продукции. Если еди-

ница составляет малую часть от общего количества, например при планирова-

нии массового и крупносерийного производства, то для нахождения опти-

мального решения применяют обычный симплекс-метод и округляют полу-

ченное решение до целого. В противном случае, например при планировании

производства или реализации автомобилей, округление может привести к ре-

шению, далекому от оптимального. Линейные задачи, решение которых

должно быть получено в целых числах, называют задачами целочисленного

программирования (ЦЛП).

Математическая модель, задачи ЦЛП имеет следующий вид:

(min)max

∑

→=

xcf

(2.8.1)











=∈

+==

+=≥

=≤

∑

njZx

mmibxa

mibxa

ijij

,1,

;,1,

(2.8.2)

где Z — множество целых чисел.

Для решения задачи ЦЛП может быть применен метод Гомори.

Метод Гомори содержит два этапа.

Этап 1. Решение исходной задачи обычным симплекс-методом и про-

верка решения на целочисленность. Если решение содержит хотя бы одно

дробное значение, то переходят к этапу 2, в противном случае расчет заканчи-

вается.

Этап 2. Составление дополнительного ограничения (сечения) и реше-

ние расширенной задачи обычным симплекс-методом. Дополнительное огра-

ничение (сечение) отсекает нецелочисленные решения.

Сечение обладает следующими двумя свойствами:

1) любое целочисленное решение ему удовлетворяет;

2) любое нецелочисленное решение задачи ему не удовлетворяет.

Объясним, как составляется сечение.

Пусть выполнен этап 1;

}0,...,0,,...,,,{

12211

=======

nmmmii

xxbxbxbxbxX

;

– дробное число. Рассмотрим

-е ограничение:

Так как

– дробное, а в правой части все переменные целые, то хотя

бы одно, значение

nmja

,1, +=

должно быть дробным.

Возьмем дробную часть от левой и правой частей ограничения.

Обозначим через {r} дробную часть числа r.

Дробная часть суммы не превосходит суммы дробных частей слагае-

мых, поэтому

}{...}{}{}{}...{

22112211 ninmimmimininmimmimi

xaxaxaxxaxaxax ++++≤++++

++++++++

Дробная часть произведения не превосходит произведения целого на

дробную часть, следовательно:

}{...}{}{}{...}{}{}{

22112211 innimmimmninmimmimi

axaxaxxaxaxax +++≤++++

++++++++

В результате имеем

}{...}{}{}{

2211 innimmimmi

axaxaxb +++≤

++++

Обозначим

ijij

qa =}{

}{

qb =

Тогда из последнего неравенства получаем

ininmimmim

qxqxqxq ≥+++

++++

...

2211

Отняв от левой части неравенства дополнительную неотрицательную

переменную, переходим к уравнению

inninmimmim

qxxqxqxq =−+++

+++++

12211

...

≥

При дополнении этого ограничения к исходной задаче мы получили

задачу большей размерности.

Эту задачу решают обычным симплекс-методом, т.е. переходят к этапу

Если при решении задачи симплекс-методом имеется несколько дроб-

ных решений, то дополнительные ограничения следует составлять для значе-

ния, имеющего максимальную дробную часть.

3. ТРАНСПОРТНАЯ ЗАДАЧА КАК ПРИМЕР СПЕЦИАЛЬНОЙ

ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Среди задач линейной оптимизации могут быть выделены два класса

задач со специальной структурой: транспортная задача и задача о назначениях.

Эти задачи используются для моделирования и оптимизации экономических

проблем, связанных с формированием оптимального плана перевозок, опти-

мального распределения индивидуальных контрактов на транспортировки, со-

ставления оптимального штатного расписания, определения оптимальной спе-

циализации предприятий, рабочих участков и станков, оптимального назначе-

ния кандидатов на работы, оптимального использования торговых агентов.

Критерием эффективности в данных задачах является линейная функция, ог-

раничения также линейны, поэтому для их решения могут применяться мето-

ды линейной оптимизации, например симплекс-метод. Однако специальная

структура таких задач позволяет разработать более удобные методы их реше-

ния. Некоторые из таких методов приведены в данной книге. Даны общая

формулировка задач, основные термины и определения, этапы построения ма-

тематических моделей, способы получения оптимальных решений. Также

приведены числовые примеры экономических задач, которые могут быть ре-

шены этими методами.

3.1.Построение транспортной модели

Построим транспортную модель для конкретной задачи.

Пример 3.1.1

Четыре предприятия данного экономического района для производства

продукции используют некоторое сырье. Спрос на сырье каждого из предпри-

ятий соответственно составляет: 120, 50, 190 и 110 усл. ед. Сырье сосредото-

чено в трех местах. Предложения поставщиков сырья равны: 160, 140 и 170

усл. ед. На каждое предприятие сырье может завозиться от любого поставщи-

ка. Тарифы перевозок известны и задаются матрицей





















6329

8954

2187

-й строке

-м столбце матрицы

стоит тариф на перевозку сырья

от

-го поставщика

-му потребителю,

4,3,2,1;3,2,1

. Под тарифом понима-

ется стоимость перевозки единицы сырья.

Требуется составить план перевозок, при котором общая стоимость

перевозок минимальна.

Построение математической модели

Цель задачи состоит в минимизации суммарной стоимости на перевоз-

ки. Эта цель может быть достигнута с помощью оптимальной организации пе-

ревозок сырья. Следовательно, за неизвестные можно принять количество сы-

рья, перевозимого от каждого поставщика каждому потребителю.

Пусть

– количество сырья, перевозимого от

-го поставщика

-му

потребителю. Параметры задачи – число поставщиков и потребителей, пред-

ложение и спрос сырья в каждом пункте, тарифы на перевозки.

Ограничения задачи – это ограничения на предложение и спрос сырья.

Предложения сырья всех поставщиков не должны быть меньше суммарного

спроса на него во всех пунктах потребления. В данной задаче имеет место

точное равенство между предложением и спросом.

120+50+190+110=160+140+170=470.

Количество сырья, вывозимого от каждого поставщика, должно быть

равно наличному количеству сырья. Количество сырья, доставленное каждому

потребителю, должно равняться его спросу. Последнее ограничение – условие

неотрицательности

Критерием эффективности (целевой функцией) являются суммарные

затраты

на перевозку, равные сумме произведений тарифов на перевозку, на

количество перевозимого сырья от каждого поставщика каждому потребите-

лю.

Окончательно математическая модель задачи имеет вид

min63298954287

343332312423222114131211

→+++++++++++= xxxxxxxxxxxxS











==≥

+++=++

=++

=+++

4,3,2,1;3,2,1;0

;17019050120170140160

;170

;190

;50

;120

;170

;140

;160

342414

312313

322212

312111

34333231

24232221

14131211

jix

xxx

xxxx

Целевая функция и ограничения линейны, т.е. данная задача относится

к задачам линейного программирования, однако, благодаря особой структуре,

эта задача получила специальное название: транспортная задача или транс-

портная модель.

3.2. Сбалансированные и несбалансированные транспортные

модели

В общем случае транспортная задача имеет следующий вид: дано

поставщиков продукции одного вида и

потребителей; предложение каждого

-го поставщика составляет

единиц,

mi ,1=

; спрос каждого

-го потребите-

ля –

единиц,

nj ,1=

; тарифы перевозок равны

mi ,1=

;

nj ,1=

. Требуется

определить оптимальный план перевозок продукции (т.е. количество продук-

ции, перевозимой от каждого поставщика каждому потребителю), при кото-

ром суммарная стоимость перевозок минимальна. Заметим, что транспортная

модель строится при условии линейной зависимости стоимости перевозок от

количества перевозимой продукции.

Пусть

– количество продукции, перевозимой от

-го поставщика

му потребителю

mi ,1=

;

nj ,1=

Формально транспортная задача записывается следующим образом:

∑∑

→=

ijij

xcS

min

(3.2.1)











==≥

≥

=≥

=≤

∑ ∑

∑

= =

njmix

nibx

miax

iij

,1;,1;0

;

;,1,

1 1

(3.2.2)(3.2.3)(3.2.4)(3.2.5)

Определение 3.2.1

Совокупность чисел

)(

mi ,1=

nj ,1=

; удовлетворяющая ограниче-

ниям (3.2.2)–(3.2.5), называется планом перевозок или планом транспортной

задачи.

Решить транспортную задачу – это значит найти такие значения

(

mi ,1=

nj ,1=

), которые удовлетворяют ограничениям (3.2.2) – (3.2.5) и дос-

тавляют минимум целевой функции (3.2.1). Целевая функция (3.2.1) определя-

ет суммарную стоимость перевозок. Ограничения (3.2.2) соответствуют тому,

что количество продукции, вывозимой от

-го поставщика, не должно превос-

ходить предложения

-го поставщика (для всех поставщиков). Ограничения

(3.2.3) соответствуют тому, что количество продукции, ввозимой

-му потре-

бителю, должно полностью удовлетворять спрос

-го потребителя (для всех

потребителей). Ограничения (1.4) соответствуют тому, что суммарное пред-

ложение не должно быть меньше суммарного спроса.

Определение 3.2.2

Задача (3.2.1)–(3.2.5) называется несбалансированной транспортной

моделью (задачей).

Определение 3.2.3

Задача (3.2.1)-т-(3.2.5), в которой ограничения (3.2.2)–(3.2.4) имеют

вид равенств, называется сбалансированной транспортной моделью (зада-

чей).

Покажем, что любую несбалансированную транспортную модель мож-

но свести к сбалансированной.

Пусть суммарное предложение больше суммарного спроса, т.е.

∑ ∑

= =

≥

1 1

(3.2.6)

Введем фиктивного (

)-го потребителя, спрос которого

∑ ∑

= =

−=

jin

bab

1 1

а тариф на перевозку этому потребителю от всех поставщиков равен 0.

miC

,1,0

Очевидно, при этом неравенства (3.2.2) и (3.2.3) перейдут в равенство,

и к ним добавится ограничение (равенство) для (

)-го пункта потребления.

∑ ∑

= =

1 1

Естественно, что в реальных задачах суммарное предложение может

быть меньше суммарного спроса, т.е.

∑ ∑

= =

1 1

(3.2.7)

Транспортные задачи, содержащие ограничение (3.2.7), также являют-

ся несбалансированными и могут быть сведены к сбалансированным с помо-

щью ввода фиктивного (

)-го поставщика, предложение которого

∑∑

−=

aba

стоимость перевозки от (

)-го поставщика нулевая,

njC

,1,0

Неравенство (3.2.7) перейдет в равенство

∑ ∑

= =

1 1

Рассмотрим сбалансированную транспортную задачу

∑∑

→=

ijij

xcS

min

(3.2.8)











==≥

∑∑

∑

njmix

njbx

miax

jij

iij

,1;,1;0

;

;,1,

(3.2.9)(3.2.10)(3.2.11)(3.2.12)

Как отмечалось выше, для решения задачи может быть применен сим-

плекс-метод, но ее особая структура (все ограничения имеют вид равенств, в

которые неизвестные входят с коэффициентами, равными 1) позволяет ре-

шать ее более простыми методами.

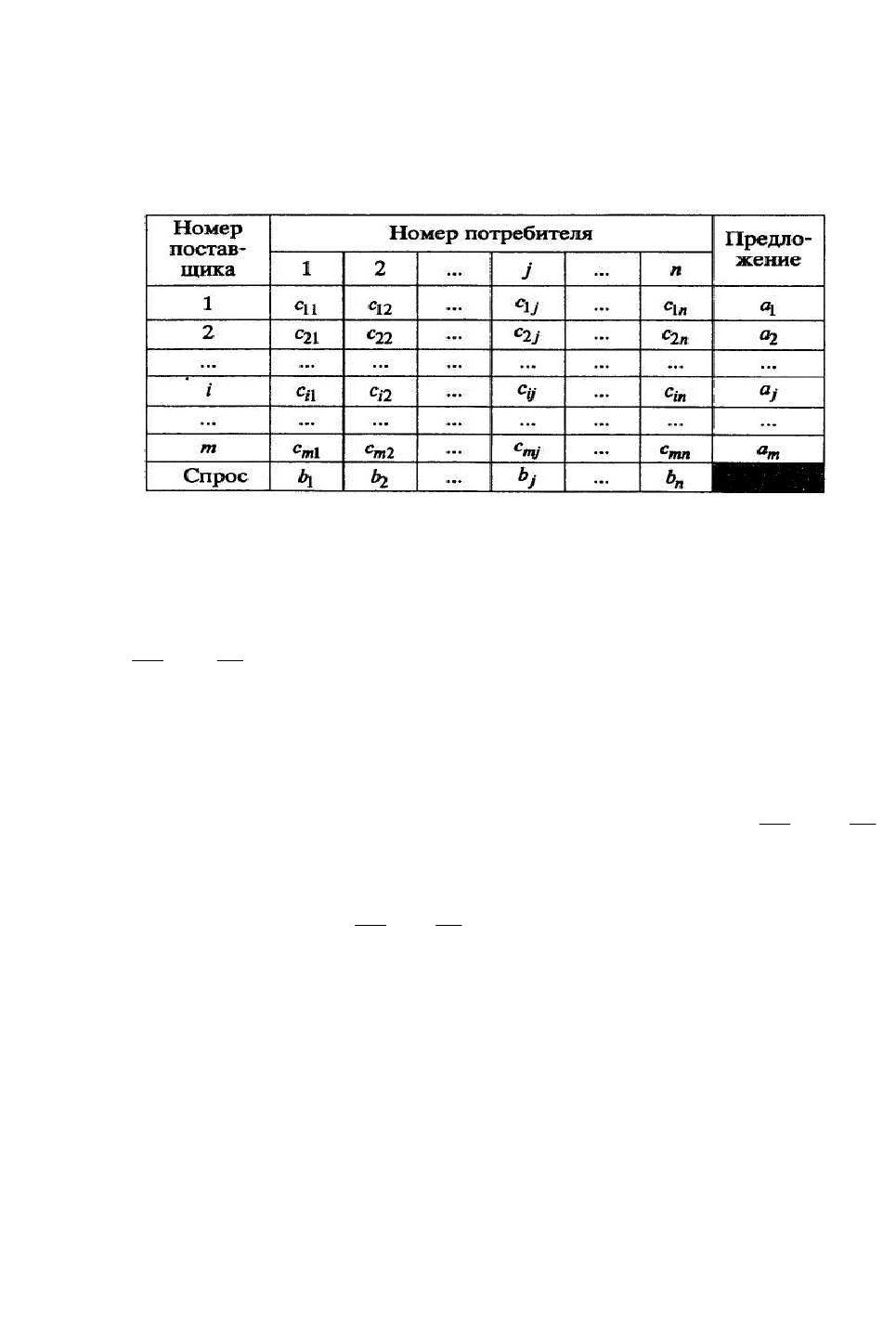
Для решения транспортной задачи составляют транспортную таблицу

(табл. 3.2.1).

Таблица 3.2.1

В левой колонке и верхней строке таблицы записаны соответственно

номера поставщиков и потребителей. В правой колонке и нижней строке запи-

саны, соответственно, предложения каждого поставщика и спрос каждого по-

требителя. В правом верхнем углу клетки, стоящей на пересечении

-й строки

-го столбца, стоит тариф

на перевозку от

-го поставщика

-му потре-

бителю (

mi ,1=

nj ,1=

Решение транспортной задачи записывают в клетки транспортной таб-

лицы: на пересечении

-й строки и

-го столбца записывается значение

Решение транспортной задачи, как и решение ОЗЛП, состоит из двух

этапов:

1 этап. Нахождение начального плана перевозок (

mi ,1=

;

nj ,1=

удовлетворяющего ограничениям (3.2.9) – (3.2.12);

2 этап. Улучшение начального плана перевозок и получение оптималь-

ного плана перевозок (

mi ,1=

;

nj ,1=

, доставляющего минимум функции

(3.2.8).

Заметим, что общее число неизвестных в транспортной задаче равно

. Уравнения (3.2.9), (3.2.10) не являются линейно-независимыми, так как

их правые части связаны условием (3.2.11). Число линейно-независимых урав-

нений в ограничениях транспортной задачи равно, следовательно, не

, а

−

. Таким образом, число неизвестных больше числа связывающих их

уравнений так же, как и в основной задаче линейного программирования.

Систему уравнений (3.2.9), (3.2.10) можно разрешить относительно

−

базисных переменных. Остальные

)1(

−

nmmn

переменных являются

свободными. Каждое решение транспортной задачи находят следующим обра-

зом: свободные

)1(

−

nmmn

переменные полагаются равными нулю, а базис-

ные

−

переменные находят из системы ограничений (3.2.9) – (3.2.10).

Полученное решение проверяют на оптимальность. Если решение неоптималь-

но, то осуществляют переход к новому решению путем изменения списка ба-

зисных переменных. Эти действия повторяют до тех пор, пока не будет полу-

чено оптимальное решение, доставляющее минимум целевой функции (3.2.8).

3.3. Определение начального плана транспортировок. Методы "се-

веро-западного" угла, минимального элемента, Фогеля

Рассмотрим три метода нахождения начального решения транспортной

задачи: метод "северо-западного" угла, метод минимального элемента и метод

Фогеля.

Метод "северо-западного" угла

Шаг 1. Составляют транспортную таблицу.

Шаг 2. Транспортную таблицу начинают заполнять с левого верхнего

(северо-западного) угла. При заполнении двигаются по строке вправо и по

столбцу вниз. В клетку, находящуюся на пересечении первой строки и перво-

го столбца, помещается максимально возможное число единиц продукции,

разрешенное ограничениями на предложение и спрос:

),min(

1111

bax =

. Если

ba <

, то

111

ax =

и предложение первого поставщика полностью исчерпано.

Первая строка вычеркивается, и двигаются по столбцу вниз. В клетку, нахо-

дящуюся на пересечении первого столбца и второй строки, помещается мак-

симально возможное число единиц продукции, разрешенное ограничениями

на предложение и спрос:

),min(

11221

abax −=

. Если

211

aab <−

, то

1121

abx −=

Спрос первого потребителя удовлетворен. Первый столбец вычеркивают и

двигаются по второй строке вправо. Заполнив клетку, стоящую на пересече-

нии второй строки и второго столбца, переходят к заполнению следующей

третьей клетки второй строки, либо второго столбца. Процесс продолжают до

тех пор, пока не исчерпается предложение и не удовлетворится спрос. По-

следняя заполненная клетка находится в последнем

-м столбце и последней

-й строке.

Пример 3.3.1

Определить начальное решение по методу "северо-западного" угла для

транспортной задачи из примера 3.1.1.

Решение.

Транспортная таблица имеет следующий вид (табл. 3.3.1):

Таблица 3.3.1

В первую клетку помещают:

120)120,160min(

==x

. Спрос первого по-

требителя полностью удовлетворен, первый столбец вычеркивают. Остаток

сырья в первом пункте составляет: 160–120=40 усл. ед. Двигаемся по первой

строке вправо

40)50,120160min(

=−=x

. Предложение поставщика исчерпано,

первая строка вычеркивается. Второму потребителю не хватает 50–40=10 усл.

ед. Двигаемся по второму столбцу вниз

10)4050,140min(

=−=x

; Второй стол-

бец вычеркивается. Двигаемся по второй строке вправо

130)90,10140min(

=−=x

. Вторая строка вычеркивается. Двигаемся по третьему

столбцу вниз

60)130190,170min(

=−=x

. Спрос третьего потребителя удовле-

творен. Двигаемся по третьей строке вправо

110)110,160170min(

=−=x

. Табли-

ца заполнена. Число ненулевых значений

3,1=i

;

4,1=j

равно 6. Число ба-

зисных переменных задачи 3+4–1=6. Остальные 3*4–6=6 переменных являют-

ся свободными, их значения равны нулю.

Начальный план перевозок имеет вид













====

1106000

0130100

0040120

34333231

24232212

14131211

xxxx

Стоимость перевозок по этому плану составляет

32206*1103*609*1305*108*407*120

=+++++=S

Метод "северо-западного" угла – наиболее простой метод нахождения

начального решения. План перевозок, полученный по этому методу, обычно

бывает достаточно далек от оптимального.

Метод минимального элемента

Шаг 1. Составляют транспортную таблицу.

Шаг 2. Выбирают клетку таблицы, которой соответствует минимальное

значение тарифа, и переходят на шаг 3.

Шаг 3. В выбранную клетку аналогично методу "северо-западного" уг-

ла помещают максимально возможное число единиц продукции, разрешенное

ограничениями на предложение и спрос. После этого, если предложение про-

изводителя исчерпано, вычеркивают соответствующую строку; если спрос

удовлетворен, вычеркивают соответствующий столбец.

Если все клетки заполнены или вычеркнуты, то план перевозок постро-

ен. В противном случае переходят к шагу 2 без учета заполненных и вычеркну-

тых клеток.