Патудин В.М., Блем А.Г. Математическая экономика

Подождите немного. Документ загружается.

– число единиц продукции

-го вида,

mi ,1=

;

– число единиц оборудования;

– фонд времени работы оборудования

-го типа,

nj ,1=

;

– производительность оборудования

-го типа по производству из-

делий

-го вида,

mi ,1=

;

nj ,1=

;

– себестоимость изготовления единицы продукции

-го вида на

оборудовании

-го типа,

mi ,1=

;

nj ,1=

;

3) Управляющие переменные

mi ,1=

nj ,1=

– это время, в течение

которого оборудование

-го типа занято изготовлением продукции

-го вида.

4) Область допустимых решений определяется ограничениями (2.2.6)

по фонду времени, ограничениями (2.2.7) по номенклатуре и условиями неот-

рицательности











==≥

=+++

≤+++

njmix

bxaxaxa

Txxx

mmnmnmmmm

nmnnn

,1,,1,0

;...

...............................................

;...

...............................................

;...

2211

22222222121

11112121111

222212

112111

(2.2.6) (2.2.7)(2.2.8)

5) Критерий оптимальности задается функцией

∑∑

= =

→=

ijij

xcС

1 1

min

, (2.2.9)

где

– суммарная себестоимость.

(2.2.6) – (2.2.9) – линейная математическая модель задачи. Она содер-

жит

неизвестных (управляющих переменных) и

ограничений, не

считая условий (2.2.8). После расчета модели определяется оптимальная за-

грузка оборудования, т.е. время в течение которого оборудование каждого ти-

па занято изготовлением продукции каждого вида.

После изучения данного раздела целесообразно решить задачи 6-7

контрольной работы № 2.

Раскрой материала

На раскрой (распил) поступает материал нескольких видов в опреде-

ленном количестве. Из этого материала необходимо изготовить различные из-

делия. Материал может быть раскроен разными способами. Каждый способ

имеет свою себестоимость и позволяет получить разное количество изделий

каждого вида. Определить способ раскроя, при котором суммарная себестои-

мость минимальна.

Составление математической модели.

1) Цель – минимизация себестоимости раскроя.

2) Параметры:

– число различных видов материала, поступающего на раскрой;

– количество материала

-го вида,

nj ,1=

;

– число различных видов изделий, которые надо изготовить;

– исло изделий

-го вида,

mi ,1=

;

– число различных способов раскроя;

ijk

– исло изделий

-го вида, которое можно получить из единицы ма-

териала

-го вида при

-м способе раскроя,

mi ,1=

nj ,1=

lk ,1=

;

– ебестоимость раскроя единицы материала

-го вида

-м

способом,

nj ,1=

lk ,1=

3) Управляющие переменные

– количество единиц материала

го вида, раскраиваемых

-м способом,

nj ,1=

lk ,1=

4) Область допустимых решений определяется ограничениями по ко-

личеству исходного материала (2.2.10), ограничениями по выпуску (2.2.11) и

условиями неотрицательности управляющих переменных (2.2.12).











==≥

=+++

nknjx

bxaxaxa

dxxx

mnlmnlmm

nlnl

nnlnn

,1,,1,0

;...

...............................................

;...

...............................................

;...

12121111

221221211211

111211211111

222212

112111

(2.2.10)(2.2.11)(2.2.12)

5) Критерий оптимальности задается формулой

∑∑

= =

→=

jkjk

xcС

1 1

min

(2.2.13)

(2.2.10) – (2.2.13) – линейная математическая модель поставленной за-

дачи. Она содержит

неизвестных (управляющих переменных) и

ог-

раничений, не считая условий неотрицательности переменных

. После рас-

чета модели определяется количество материала каждого вида, раскраиваемо-

го различными способами.

Вместо критерия минимизации себестоимости в задаче может быть

взят, например, критерий минимизации отходов. В этом случае в условии

должно быть задано количество отходов, получаемых при каждом способе

раскроя для единицы материала каждого вида.

После изучения данного раздела целесообразно решить задачи 8-11

контрольной работы № 2.

Составление плана реализации товара

Фирма реализует различные товары, используя при этом определен-

ный набор средств (технических, людских, денежных).

Общий запас средств, число средств каждого вида, используемых при

реализации единицы любого товара и прибыль от его продажи заданы. Надо

сформировать план реализации товаров, приносящий фирме максимальную

прибыль.

Построение математической модели.

1) Цель — максимизации прибыли.

2) Параметры:

– число различных видов реализуемых товаров;

– число разных видов средств;

– запас средств

-го вида,

mi ,1

;

– число средств

-го вида, используемых для реализации единицы

товара

-го вида,

mi ,1

nj ,1

;

– прибыль от реализации единицы товара

-го вида,

nj ,1

3) Управляющие переменные

nj ,1

– количество реализуемого то-

вара

-го вида;

4) Область допустимых решений формируют ограничения по запасам

средств и условия неотрицательности управляющих переменных.











=≥

≤+++

njx

bxaxaxa

mnmnmm

,1,0

;...

...............................................

;...

2211

22222121

11212111

(2.2.14)

5) Критерий оптимальности определяется по формуле

∑

→=

xPP

max

, (2.2.15)

где

– суммарная прибыль.

В результате расчета линейной математической модели (2.2.14),

(2.2.15) определяется количество реализуемых товаров каждого вида, обеспе-

чивающее фирме максимальную прибыль.

После изучения данного раздела целесообразно решить задачи 12-13

контрольной работы № 2.

2.3. Графический метод решения задачи линейного программирования

Если число переменных в задаче линейного программирования (ЗЛП)

равно двум, а ограничениями является система неравенств, то задачу можно

решать графическим методом.

Пример 2.3.1

При продаже двух видов товара используется 4 типа ресурсов. Норма

затрат ресурсов на реализацию единицы товара, общий объем каждого ресур-

са заданы в табл. 2.3.1.

Таблица 2.3.1

Норма затрат ресурсов на товары

Ресур-

сы

1-го вида 2-го вида

Общее количество

ресурсов

Прибыль от реализации одной единицы товара первого вида составляет

2 усл. ед., второго вида – 3 усл. ед.

Требуется найти оптимальный план реализации товаров, обеспечи-

вающий торговому предприятию максимальную прибыль.

Решение.

Это задача составления плана реализации товара (пример 2.2.5) при

=2,

=4.

Математическая модель имеет вид

max32

→+= xxP

(2.3.1)











≥

≤

≤+

;124

;164

;82

;1222

(2.3.2)

В модели управляющие переменные

– количество реализуемых

изделий первого и второго вида, соответственно,

– прибыль. Система нера-

венств включает ограничения по ресурсам. Количество ресурсов на реализа-

цию товаров первого и второго вида не превышает общего количества ресурсов

каждого типа.

Графическое решение

Построим в плоскости

xx ×

область допустимых решений. Каждое не-

равенство системы (2.3.2) определяет в плоскости

xx ×

полуплоскость, лежа-

щую выше или ниже прямой, определяемой соответствующим уравнением.

Построим прямые

;124

;164

;82

;1222

Рассмотрим точку с координатами

0;0

== xx

. Подставив их в первое

неравенство, получаем

120

≤

– верно, следовательно, искомая полуплоскость

лежит ниже прямой

1222

=+ xx

; остальные полуплоскости находятся анало-

гичным образом.

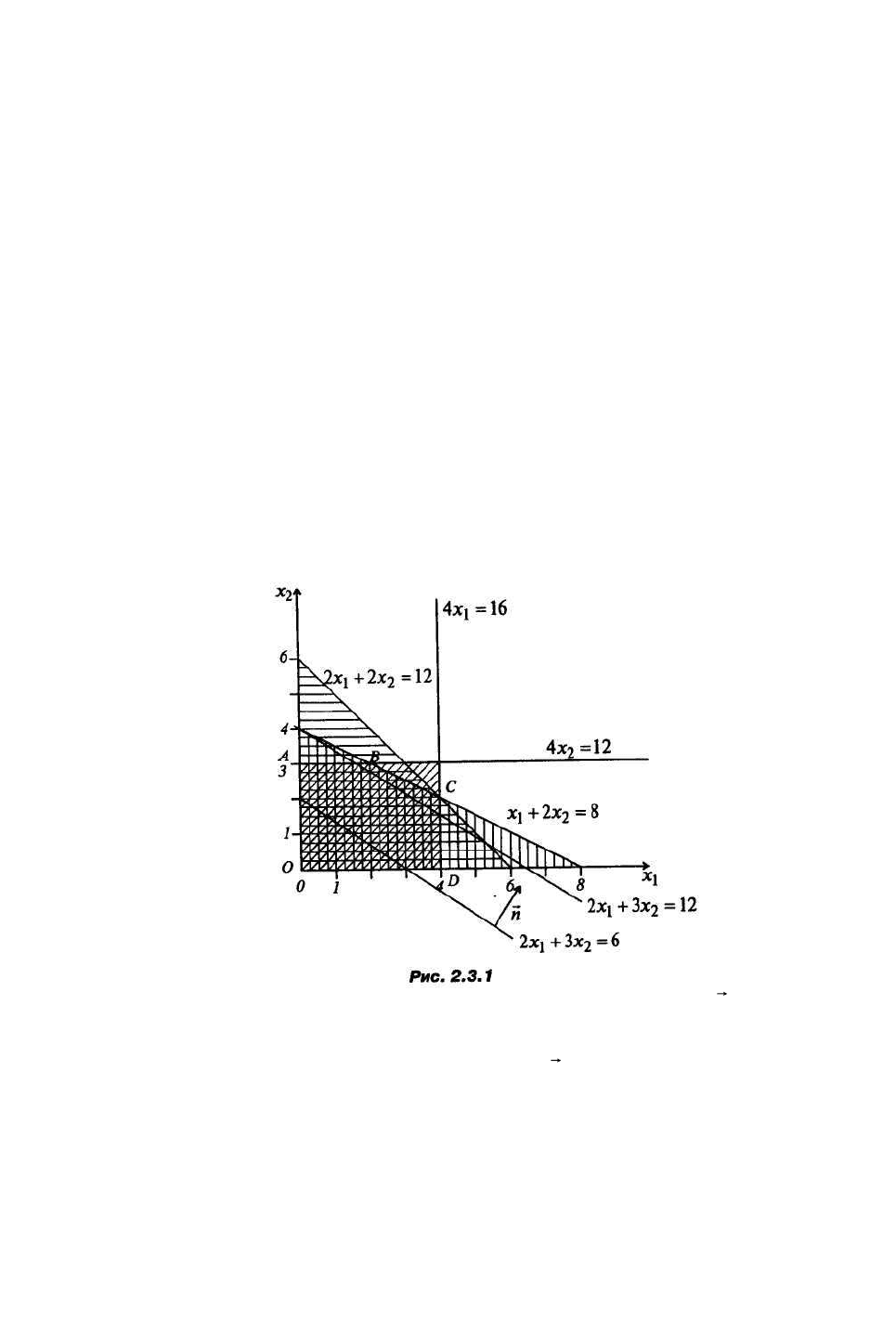
Область

OABCD

– область решения задачи.

Для нахождения максимального значения

проверим граничные точки

из области решений.

Построим две линии уровня:

.1232

;632

Функция

возрастает в направлении вектора-нормали

)3;2(=n

, следо-

вательно, минимум находится в точке (0;0). Максимум определяем, передви-

гая нашу линию уровня в направлении вектора

параллельно самой себе до

тех пор, пока хотя бы одна ее точка будет принадлежать области допустимых

решений.

В данном случае это точка:

2,4

== xx

;

при этом

142342

Таким образом, для получения максимальной прибыли в размере 14

усл. ед. надо продать 4 изделия первого вида и 2 изделия второго вида.

Изложенный выше графический метод применим для решения задач

линейного программирования следующего вида:

max(min)

2211

→+= xcxcf

(2.3.3)











+=≥+

=≤+

.,1,

;,1,

12211

mmibxaxa

mibxaxa

iii

(2.3.4)

Алгоритм решения ЗЛП графическим методом.

1) Записывают уравнения прямых, соответствующих ограничениям

(2.3.4), и строят их на плоскости

oxx

2) Определяют области, в которых выполняются ограничения задачи.

Для этого выбирают произвольную точку на плоскости

oxx

и подставляют ее

координаты в первую часть одного из неравенств. Если неравенство верно, то

искомая полуплоскость находится с той же стороны от прямой, что и точка; в

противном случае искомая полуплоскость лежит с противоположной стороны

от прямой. Эти действия последовательно выполняются для всех неравенств

(2.3.4).

3) Определяют область допустимых решений задачи как область пере-

сечения

полуплоскостей, соответствующих

ограничениям задачи.

4) Определяют направление возрастания (убывания) целевой функции

.Это можно сделать двумя способами. Можно построить вектор-нормаль

),(

ccn =

, его направление показывает направление возрастания функции

, в

противоположном направлении функция убывает. Можно просто построить

две линии уровня функции

Kf =

;

Kf =

; (

, KK

) – произвольные константы,

KK ≠

), и по их расположению определить направление возрастания (убыва-

ния) функции.

5) Определяют граничную точку (точки) области допустимых реше-

ний, в которых целевая функция принимает максимальное или минимальное

значение.

6) Вычисляют значения найденной точки, решая совместно уравнения,

задающие прямые, на пересечении которых находится эта точка, или выявляя

уравнение граничной прямой области допустимых решений, с которой совпа-

дает линия уровня целевой функции.

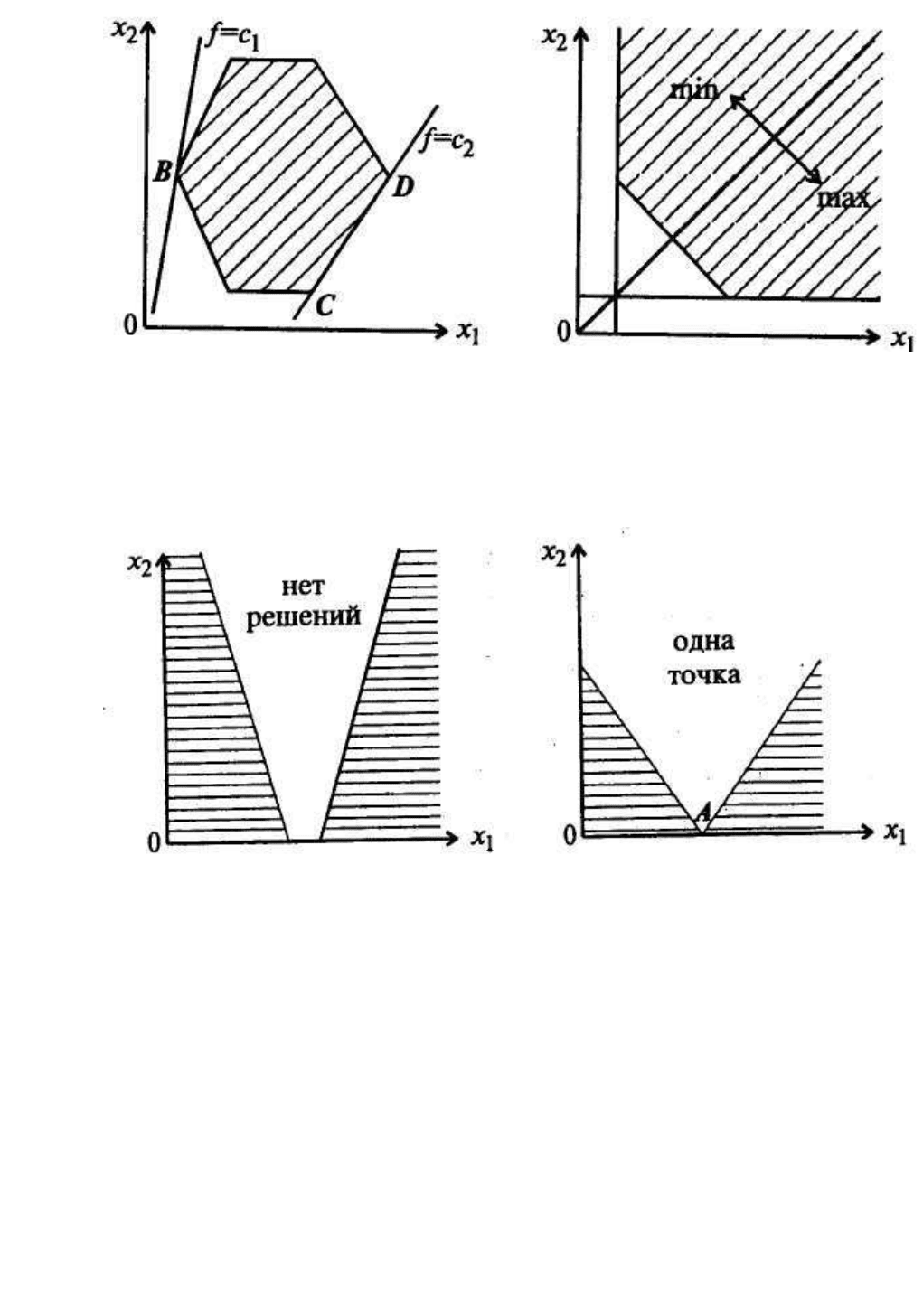
Возможны следующие варианты области допустимых решений (рис.

2.3.2 – рис. 2.3.5):

На рис. 2.3.2, 2.3.3 показаны варианты пересечения линии уровня це-

левой функции с областью допустимых решений. Может быть единственное

решение – точка В, бесконечно много решений – отрезок CD (рис.2.3.2), мак-

симальным (минимальным) значением целевой функции может быть

∞

(рис.2.3.3).

После изучения данного раздела целесообразно решить задачу 1 кон-

трольной работы № 3.

Рис. 2.3.2

Область допустимых решений - замкнутое

множество (многоугольник)

Рис. 2.3.3

Область допустимых решений – открытое

множество

Рис. 2.3.4

Область допустимых решений – пустое

множество (система ограничений (2.3.2)

несовместна

Рис. 2.3.5

Область допустимых решений состоит из

единственной точки А

2.4. Основная задача линейного программирования

В произвольной форме линейная математическая модель или задача

линейного программирования имеет вид (2.1.1) – (2.1.4).

Наиболее распространенный метод ее решения – симплекс-метод. За-

метим, что в случае двух переменных область допустимых решений, как пра-

вило, представляет собой замкнутый многоугольник (рис. 2.3.2). Для

пере-

менных областью допустимых решений является многомерный многогранник,

подобный симплексу. Оптимальное решение, как правило, это вершина (гра-

ничная точка) такого многогранника. Симплекс-метод заключается в последо-

вательном целенаправленном обходе вершин симплекса. В каждой следующей

граничной точке симплекса значение целевой функции, в общем случае,

улучшается.

Для применения симплекс-метода задачу следует записать в канониче-

ской форме:

max...

2211

→+++=

xcxcxcf

(2.4.1)











=≥

=+++

njx

bxaxaxa

mnmnmm

,1,0

;...

...............................................

;...

2211

22222121

11212111

(2.4.2)

В канонической форме записи все переменные неотрицательны, огра-

ничениями являются уравнения, и требуется найти такие значения

njx

,1, =

при которых целевая функция имеет максимум.

Переход к канонической форме записи производится с помощью сле-

дующих простых действий.

1) Если требуется найти минимум

, то заменяя

на -

, переходят к

задаче максимизации, так как

)max()min(

−

2) Если ограничение содержит неравенство со знаком

≤

, то от него пе-

реходят к равенству, добавляя в левую часть ограничения дополнительную не-

отрицательную переменную.

3) Если ограничение содержит неравенство со знаком

≥

, то от него пе-

реходят к равенству, вычитая из левой части дополнительную неотрицатель-

ную переменную.

4) Если в задаче какая-либо из переменных произвольна, то от нее из-

бавляются, заменяя ее разностью двух других неотрицательных переменных.

Например, для произвольной переменной

kkkk

xxxx

−=,

, где

0,0 ≥≥

Пример 2.4.1

Записать в канонической форме задачу

.min325

321

→−+=

xxxf











≥≥

=++

≤−−

≥+−

.0,0

;20725

;728

;1032

321

xxx

Решение

3211

325

xxxff

+−−=−=

Вычитая дополнительную неотрицательную переменную

из левой

части первого неравенства, переходим к равенству.

Добавляя дополнительную неотрицательную переменную к левой час-

ти второго неравенства, также переходим к равенству.

Произвольную переменную

заменяем разностью двух неотрица-

тельных переменных

0,0,

76763

≥≥−=

xxxxx

Окончательно получаем каноническую форму записи

max3325

76211

→−+−−=

xxxxf











≥≥≥≥≥≥

=−++

=+−−−

=−−+−

.0,0,0,0,0,0

;207725

;7228

;1032

765421

7621

57621

47621

xxxxxx

xxxx

xxxxx

Задача (2.4.1) — (2.4.3) называется основной задачей линейного про-

граммирования (ОЗЛП).

ОЗЛП не всегда имеет решение.

Во-первых, уравнения (2.4.2) могут оказаться несовместными.

Во-вторых, уравнения (2.4.2) могут оказаться совместными не в облас-

ти неотрицательных решений.

В-третьих, допустимые решения (2.4.2), (2.4.3) существуют, но среди

них нет оптимального: функция

не ограничена в области допустимых ре-

шений.

Предположим, что все уравнения (2.4.2) линейно независимы, т.е. вы-

ражают независимые друг от друга условия задачи. Если это не так, то лишние

уравнения надо просто исключить. Задачу (2.4.1) – (2.4.3) имеет смысл решать,

когда число уравнений в системе ограничений (2.4.2) меньше числа входящих

в них неизвестных:

. В противном случае, если

, то система (2.4.2)

имеет единственное решение, и задача максимизации функции (2.4.1) не имеет

смысла; если

, то система (2.4.2) переопределена и в общем случае не

имеет решений.

Если

, то система (2.4.2) имеет бесконечное множество решений и

среди них можно выбрать оптимальное, доставляющее максимум функции

(2.4.1).

2.5.Симплекс-метод

Симплекс-метод является методом направленного перебора решений

системы (2.4.2) – (2.4.3). Каждое следующее решение улучшает значение це-

левой функции.

Симплекс-метод включает два этапа:

1) определение начального решения, удовлетворяющего ограничениям

(2.4.2), (2.4.3);

2) последовательное улучшение начального решения и получение оп-

тимального решения задачи (2.4.1) – (2.4.3).

Любое решение задачи линейного программирования называется

опорным планом задачи.

Система (2.4.2) содержит

линейно независимых уравнений, и их

число меньше числа неизвестных, входящих в систему, следовательно, систе-

му (2.4.2) можно разрешить относительно

неизвестных, например

xxx

,...,,

, выразив их через остальные неизвестные











=+++

....

.............................................

;...

221122

111111

mnmnmmmm

nnmm

bxaxax

(Коэффициенты

njmia

,1,,1, ==

в полученной системе, естественно,

отличны от коэффициентов системы (2.4.2), но для простоты обозначены той

же буквой).

Данный переход осуществляется с помощью элементарных алгебраи-

ческих преобразований, включающих умножение правой и левой частей урав-

нений на одно и то же число и их сложение и не влияющих на значение реше-

ний системы (2.4.2).

После указанных преобразований задача (2.4.1) – (2.4.3) запишется в

следующем виде:

∑

→=

xcf

max

(2.5.1)











=≥

=+++

.,1,0

;...

.............................................

;...

221122

111111

njx

bxaxax

mnmnmmmm

nnmm

(2.5.2)(2.5.3)

Форма записи (2.5.1) – (2.5.3) называется стандартной.

Алгоритм решения системы (2.5.1) — (2.5.3) симплекс-методом