Патудин В.М., Блем А.Г. Математическая экономика
Подождите немного. Документ загружается.

71
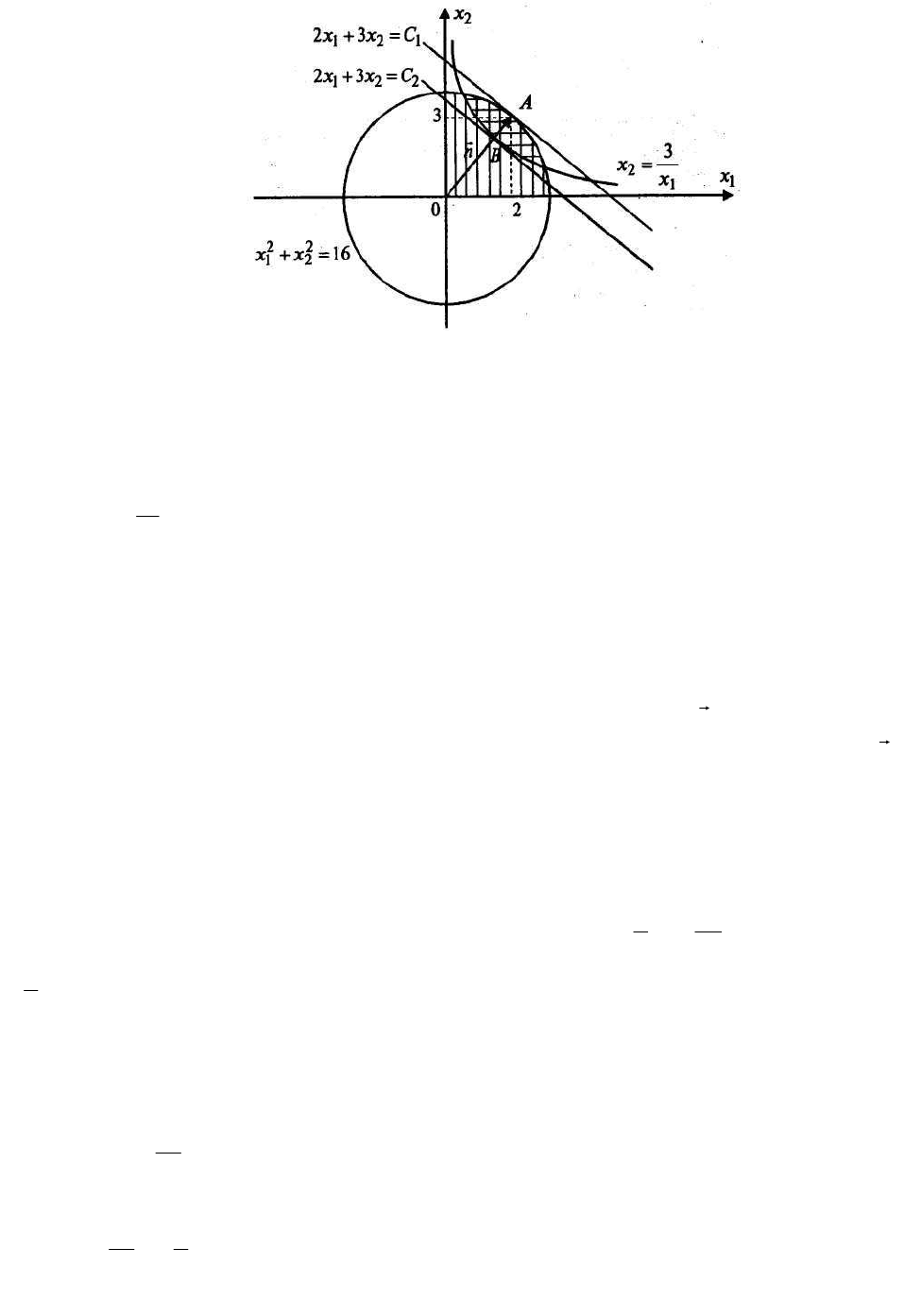
Рис. 4.2.1
Ограничения
0
1
≥x
,
0
2
≥x
выделяют на плоскости
21
0xx
первую чет-
верть.
Границей полуплоскости, соответствующей первому ограничению,
является гипербола
1
2
3
x
x =
Неравенство выполняется для точек, лежащих выше гиперболы.
Границей полуплоскости, определяемой вторым ограничением, являет-
ся окружность с центром в точке (0,0) и радиусом, равным 4. Искомая полу-
плоскость заштрихована вертикальной штриховкой. Область допустимых ре-
шений выделена горизонтальной штриховкой.
Функция возрастает в направлении вектора-нормали
n
с координатами
(2,3), и ее линии уровня расположены перпендикулярно вектору-нормали
n
.
Таким образом, максимум достигается в точке А, а минимум – в точке В.
Заметим, что в точке А совпадают тангенсы углов наклона касательной
к окружности
16
2
2
2
1
=+ xx
и прямой
121
32 Cxx =+
к оси
1
0x
. Тангенсы углов на-
клона касательной и прямой к оси
1
0x
определяются значениями производных
по
1
x
соответствующих функций. Для прямой
3
3
2
1
12
C
xx +−=
тангенс равен
3
2
−
.
Продифференцируем выражение
16
2
2
2
1
=+ xx
как неявную функцию от
1
x
. Получаем
0'22
221
=+ xxx
,
2
1
2
'
x
x
x −=
Приравниваем значения тангенсов, получаем
3
2
2
1
−=−
x
x
,
023
21
=− xx
72
К этому уравнению добавим уравнение окружности, которой принад-
лежит точка А.
Получаем систему
=+
=−
16
,023
2
2
2
1
21
xx
xx
Решив ее, найдем оптимальное решение
3
12
1
=x
;
13
12
2
=x
;
13
52
max
=f
Аналогично определим координату точки В, в которой тангенс угла
наклона к оси
1
0x
прямой
221
32 Cxx =+
совпадает с тангенсом угла наклона ка-
сательной к функции
3
21
=xx
.
1
2
3
x
x =
2
1
2
3
'
x
x =
Получаем уравнение
3
23
2
1
−=−
x
Вторым для нахождения координат точки является уравнение гипербо-
лы, которой принадлежит точка В:
=
−=−
3
3
23
21
2
1
xx
x
Из последней системы найдем оптимальное решение, соответствующее
минимальному значению
f
,
2
3
1
=x
,
2
2
=x
,
2
12
min
=f
4.3. Метод множителей Лагранжа
Пусть требуется решить задачу нелинейного программирования сле-
дующего вида:
max(min)),...,,(
21
→
n
xxxf
(4.3.1)
=
=
=
mnm
n
n
bxxxg
bxxxg
bxxxg
),...,,(
.................................
;),...,,(
;),...,,(
21
2212
1211
(4.3.2)
где функции
f
и
i
g
,
ni ,1=
непрерывны, и непрерывны их частные
производные по
j
x
,
nj ,1=
.

73
Для решения поставленной задачи может быть применен метод мно-
жителей Лагранжа. Объясним идею метода на примере ЗНП, зависящей от
двух переменных.
max),(
21
→xxf
bxxg =),(
21
На плоскости
21
0xx
уравнение
bxxg =),(
21
определяет график некото-
рой функции, представленный на рис. 4.3.1. На нем показаны несколько линий
уровня некоторой функции
),(
21
xxf
и выбранное в качестве примера направ-
ление ее возрастания.
Рис. 4.3.1
В точке А, в которой функция
f
достигает максимального значения,
совпадают касательные линии к графикам функций
Cxxf =),(
21
и
bxxg =),(
21
.
Следовательно, в точке А векторы-нормали к функциям
bxxg =),(
21
и
Cxxf =),(
21
пропорциональны. Обозначим эти векторы соответственно через
k
и
l
. Получаем
kl
λ
=
,
где
λ
– некоторый коэффициент пропорциональности. Координатами
векторов
l
и
k
являются значения частных производных функций
f
и
g
соот-
ветственно в точке А.
);(
21
x
f
x
f
l
∂
∂
∂
∂
=
;
);(
21
x
g
x
g
k
∂
∂
∂
∂
=
.
Из условия пропорциональности в точке А имеем
21
x
g
x
f
∂
∂
=
∂
∂
λ
;
22
x
g
x
f
∂
∂
=
∂
∂
λ
.
Для определения значений
21
, xx
, в которых функция
f
достигает мак-
симума, к этим уравнениям надо добавить условие принадлежности точки А
графику функции
bxxg =),(
21
.
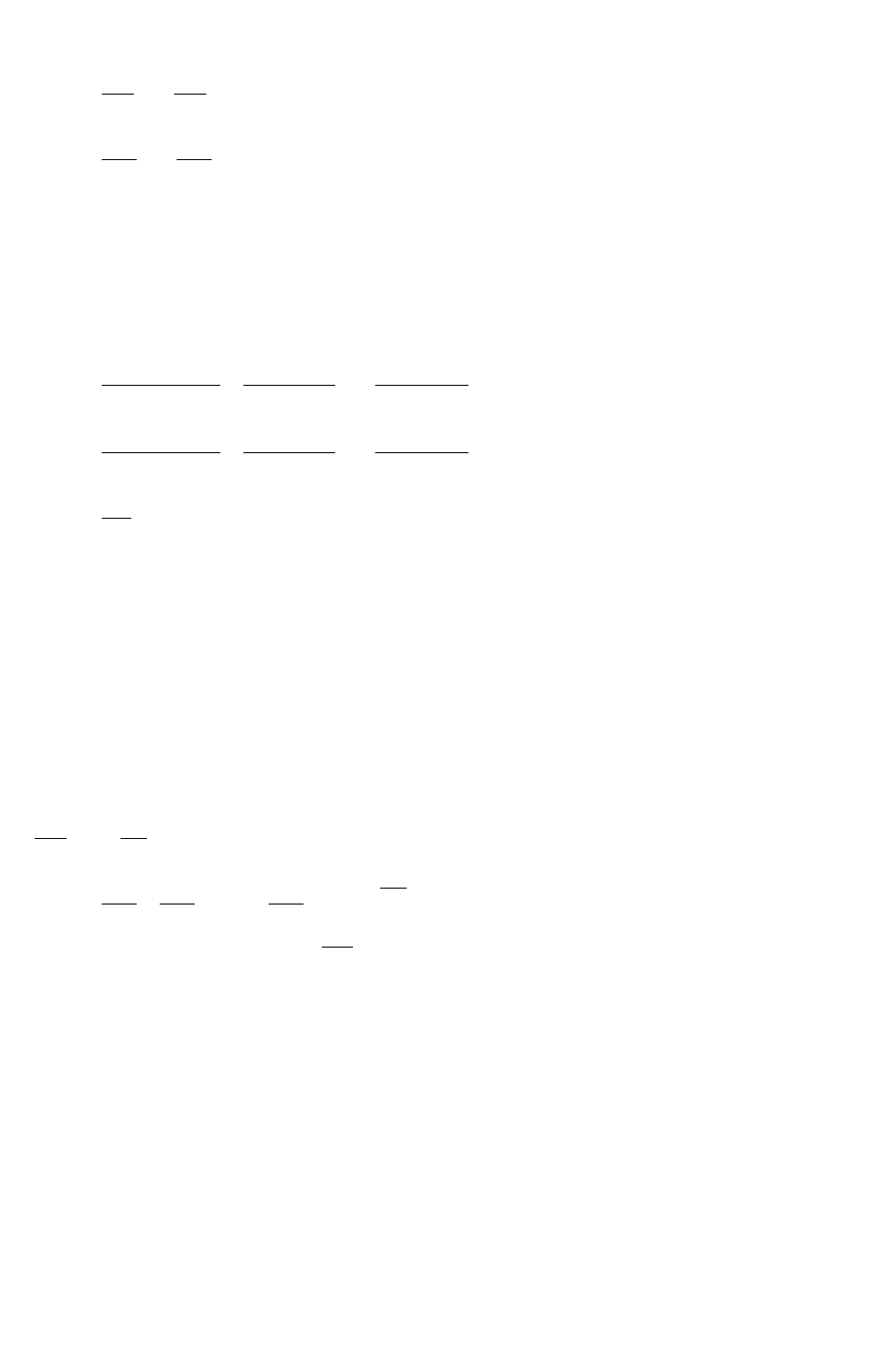
74
Окончательно получаем систему уравнений, определяющую опти-
мальное решение поставленной задачи
=
∂
∂
=
∂
∂
∂
∂
=
∂
∂
bxxg
x
g
x
f
x
g
x
f
),(
21
22
11
λ
λ
Введем новую функцию
)),((),(),,(
212121
xxgbxxfxxF −+=
λλ
.
Тогда последняя система перепишется в виде
=−=
∂
∂
=
∂
∂
−
∂
∂
=
∂
∂
=
∂
∂
−
∂
∂
=
∂
∂
0),(
0
),(),(),,(
0
),(),(),,(
21
2
21
2
21
2
21
1
21
1
21
1
21
xxgb
F
x
xxg
x
xxf
x
xxF
x
xxg
x
xxf
x
xxF
λ
λ
λ
λ
λ
Функцию
F
называют функцией Лагранжа.
Алгоритм метода множителей Лагранжа решения задачи (4.3.1),
(4.3.2)
Шаг 1. Составляют функцию Лагранжа
∑
=
−+=
m
i
niiinmn
xxxgbxxxfxxxF
1
21212121
)),...,,((),...,,(),...,,,,...,,(
λλλλ
Шаг 2. Находят частные производные функции Лагранжа по
j
x
и
i
λ
,
mi ,1=
,
nj ,1=
и приравнивают их к нулю
==
==
∂
∂
−
∂
∂
=
∂
∂
∑
=
mibxxxg
nj
x
g
x
f
x
F
ini
m
i
j
i
jj
,1,),...,,(
,1,0
21
1
λ
Шаг 3. Решают систему (4.3.3) и определяют точки, в которых функ-
ция
),...,,(
21
n
xxxf
может иметь экстремум.
Шаг 4. Проверяют полученные на шаге 3 точки на экстремум и опре-
деляют экстремальное значение функции
f
в найденной точке.
4.4. Расчет экономико-математической модели при нелинейных за-
тратах на производство
Рассмотрим применение изученных методов на примере решения зада-
чи оптимальной реализации продукции.
Пример 4.4.1

75
Фирма реализует автомобили двумя способами: через магазин и через
торговых агентов. При реализации
1
x
автомобилей через магазин расходы на
реализацию составляют
2
11
4 xx +
усл. ед., а при продаже
2
x
автомобилей через
торговых агентов расходы составляют
2
2
x
усл. ед. Найти оптимальный способ
реализации автомобилей, минимизирующий суммарные расходы, если общее
число предназначенных для продажи автомобилей составляет 200 штук.
Решение.
Составим математическую модель задачи.
Целью является минимизация суммарных расходов
2
2
2
11
4 xxxR ++=
.
Управляющие переменные – это число автомобилей, реализуемых пер-
вым и вторым способом:
1
x
и
2
x
соответственно (200 штук). Окончательно ма-
тематическая модель имеет следующий вид:
min4
2
2
2
11
→++= xxxR
.
≥
≥
=+
0
0
200
2
1
21
x
x
xx
.
Для ее расчета применим метод множителей Лагранжа. Функция Ла-
гранжа имеет вид
)200(4),,(
21
2
2
2
1121
xxxxxxxF −−+++=
λλ
.
Найдем частные производные функции
F
по
1
x
,
2
x
и
λ
и приравняем
их к нулю.
Получим следующую систему уравнений:
=−−=
∂
∂
=−=
∂
∂
=−+=
∂
∂
0200
02
042
21
2
2
1
1
xx
F
x
x
F
x
x
F
λ
λ
λ
.
Решая систему, найдем
1
x
=99,
2
x
=101,
λ
=202,
),(
21
xxf
=20398.
Определитель, составленный из вторых частных производных функций
f
по
1
x
,
2
x
, имеет вид
04
20
02
22
2
12
2
21
2
11
2
>==
∂∂
∂
∂∂
∂
∂∂
∂
∂∂
∂
xx
f
xx
f
xx
f
xx
f
Следовательно, по теореме о достаточном условии существования ус-
ловного экстремума функция
),(
21
xxf
в точке
1
x
=99,
2
x
=101 действительно
имеет экстремум.
76
02
11
2
>=
∂∂
∂
xx
f
следовательно в этой точке функция
f
имеет условный минимум.
Таким образом, для получения минимальных расходов, нужно реали-
зовать 99 автомобилей через магазин и 101 автомобиль через торговых аген-
тов. При этом расходы на реализацию составят 20398 усл. ед.
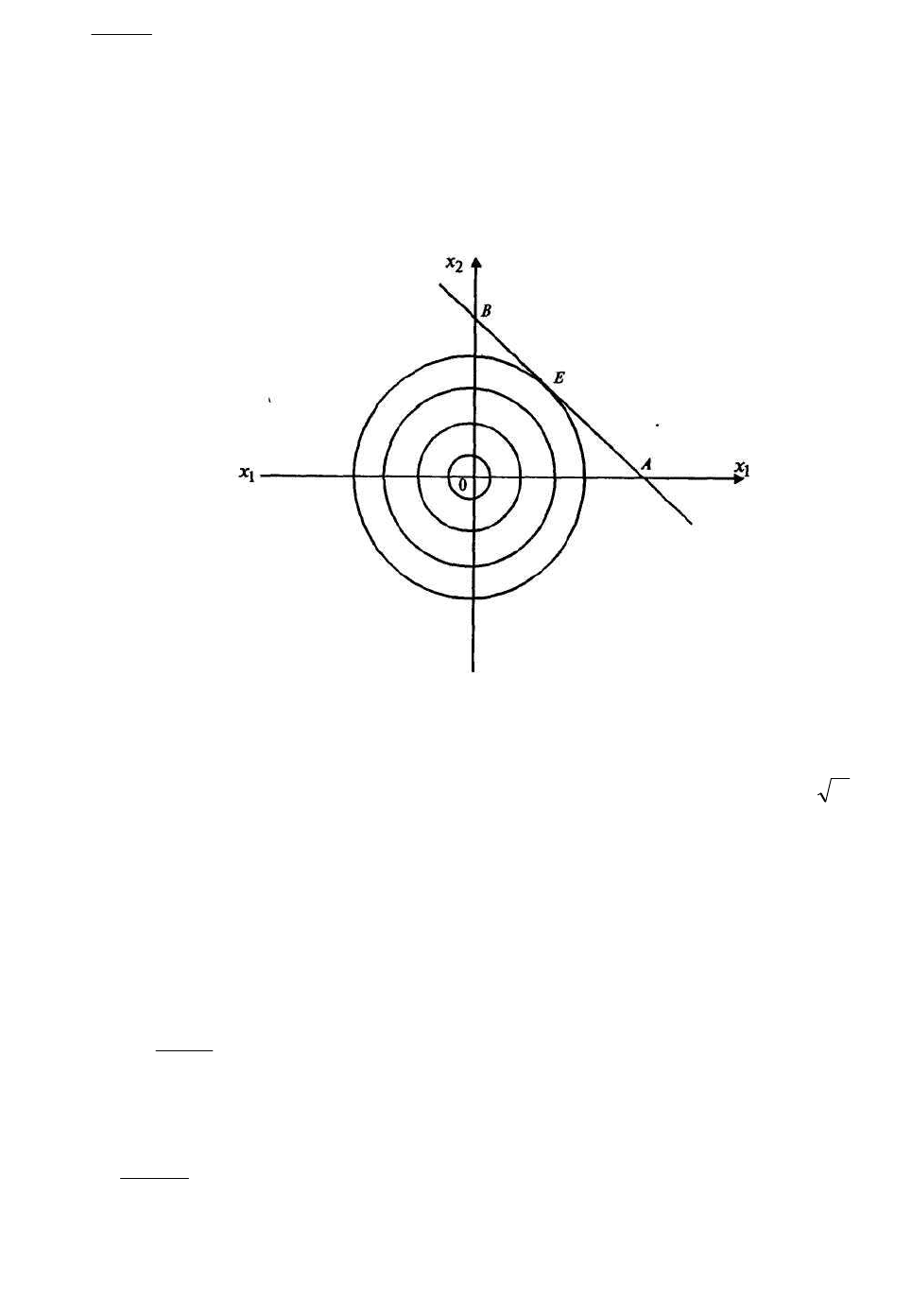
Данную задачу можно было решить и графическим методом (рис.
4.4.1).
Рис. 4.4.1
Областью допустимых решений задачи является отрезок АВ, линиями
уровня функции
4)2(4
2
2
2
1
2
21
2
1
−++=++= xxxxxf
являются концентрические
окружности
Cxx =++
2
2
2
1
)2(
с центром в точке
1
x
=-2,
2
x
=0 и радиусом
С
.
Из рисунка видно, что минимальное значение функции, принадлежа-
щее области допустимых решений, достигается в точке
E
, в которой совпада-
ют угловой коэффициент прямой
2
x
=200-
1
x
и касательной к окружности
Cxx =++
2
2
2
1
)2(
к оси
1
0x
.
Продифференцировав последнее уравнение по
1
x
, получим
2221
'2)(2 xxxx ++
,
2
1
2
2
'
x
x
x
+
−=
.
Приравняем последнее выражение к угловому коэффициенту прямой и
добавим к этому уравнению уравнение прямой, которой принадлежит точка Е.
=+
−=
+
−
200
1
21
2
21
xx
x
xx
Решив последнюю систему, найдем оптимальные значения:
1
x
=99,
2
x
=101,
),(
21
xxf
=20398.
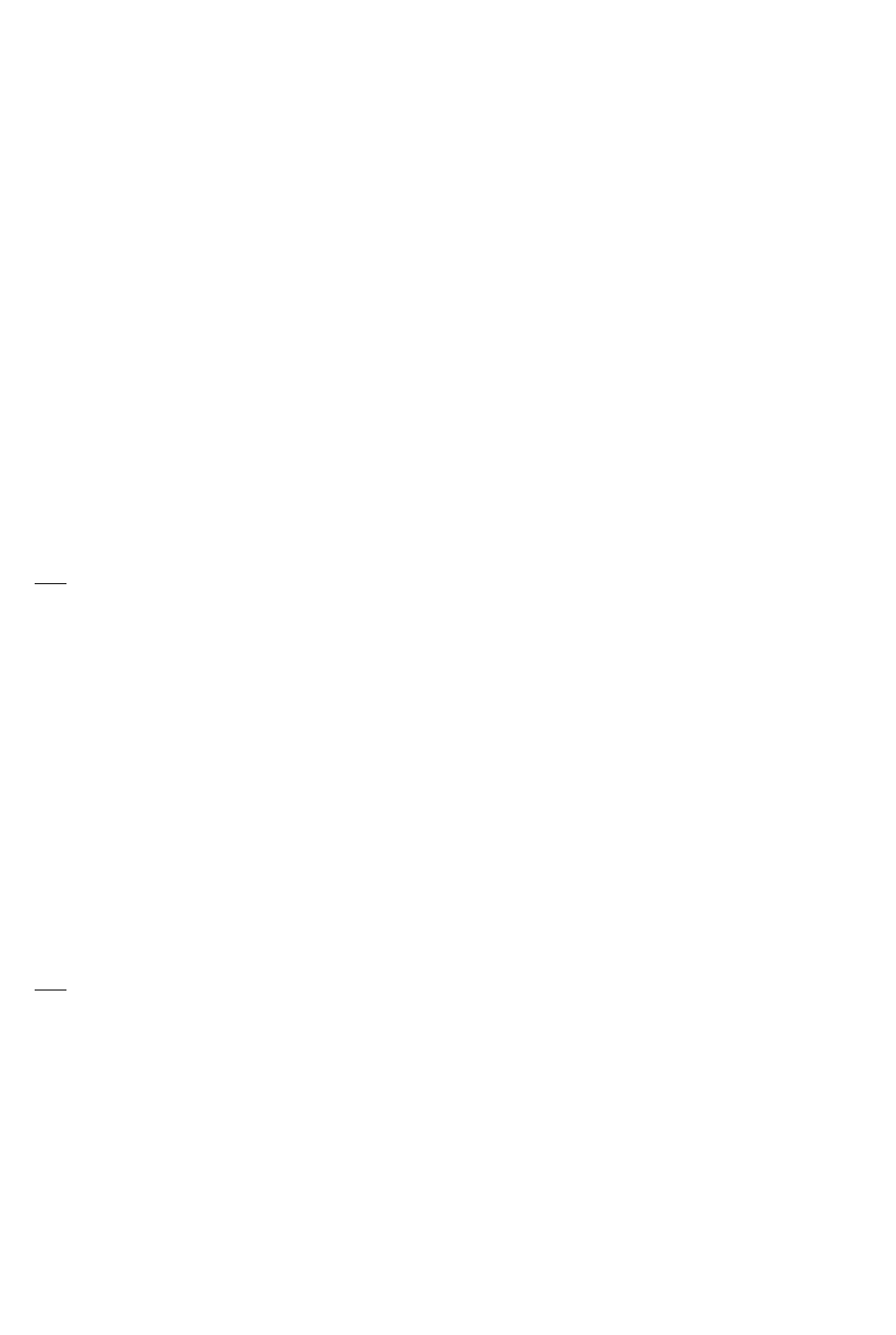
77
5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
В ряде реальных экономических и производственных задач необходи-
мо учитывать изменение моделируемого процесса во времени и влияние вре-
мени на критерии оптимальности. Для решения указанных задач используется
метод динамического планирования (динамическое программирование). Этот
метод более сложен по сравнению с методами расчета статических оптимиза-
ционных задач, изложенных выше. Также не простым делом является процесс
построения для реальной задачи математической модели динамического про-
граммирования.
5.1. Постановка задачи динамического программирования. Основ-
ные условия и область применения
Пусть рассматривается задача, распадающаяся на
m
шагов или этапов,
например планирование деятельности предприятия на несколько лет, поэтап-
ное планирование инвестиций, управление производственными мощностями в
течение длительного срока. Показатель эффективности задачи в целом обозна-
чим через W, а показатели эффективности на отдельных шагах – через
i
ϕ
,
mi ,1=
. Если W обладает свойством аддитивности, т.е.
∑
=
=
m
i
i
W
1
ϕ
, (5.1.1)
то можно найти оптимальное решение задачи методом динамического про-
граммирования.
Таким образом, динамическое программирование – это метод оптими-
зации многошаговых или многоэтапных процессов, критерий эффективности
которых обладает свойством (5.1.1). В задачах динамического программиро-
вания критерий эффективности называется выигрышем. Данные процессы
управляемые, и от правильного выбора управления зависит величина выиг-
рыша.
Определение 5.1.1. Переменная
i
x
, от которой зависят выигрыш на
i
-м
шаге и, следовательно, выигрыш в целом, называется шаговым управлением,
mi ,1=
.
Определение 5.12. Управлением процесса в целом (х) называется по-
следовательность шаговых управлений
),...,,...,,(
21 mi
xxxxx =
.
Определение 5.1.3. Оптимальное управление х* – это значение управ-
ления х, при котором значение W(x* ) является максимальным (или минималь-
ным, если требуется уменьшить проигрыш)
XxxWxWW
∈
=
)},(max{*)(*
, (5.1.2)
где Х - область допустимых управлений.
Оптимальное управление х* определяется последовательностью опти-
мальных шаговых управлений
*)*,...,*,...,*,(*
21 mi
xxxxx =

78
В основе метода динамического программирования лежит принцип оп-
тимальности Беллмана, формулирующийся следующим образом: управление
на каждом шаге надо выбирать так, чтобы оптимальной была сумма выигры-
шей на всех оставшихся до конца процесса шагах, включая выигрыш на дан-
ном шаге.
Поясним это правило. При решении задачи динамического программи-
рования на каждом шаге выбирается управление, которое должно привести к
оптимальному выигрышу. Бели считать все шаги независимыми друг от друга,
то оптимальным шаговым управлением будет то управление, которое прино-
сит максимальный выигрыш именно на данном шаге. Но, например, при по-
купке новой техники взамен устаревшей на ее приобретение затрачиваются
определенные средства. Поэтому прибыль от ее эксплуатации вначале может
быть небольшой. Однако в следующие годы новая техника будет приносить
большую прибыль. И наоборот, если руководитель примет решение оставить
старую технику для получения прибыли в текущем году, то в дальнейшем это
приведет к значительным убыткам. Данный пример демонстрирует следую-
щий факт: в многошаговых процессах все шаги зависят друг от друга, и, сле-
довательно, управление на каждом конкретном шаге надо выбирать с учетом
его будущих воздействий на весь процесс.
Другой момент, который следует учитывать при выборе управления на
данном шаге, – это возможные варианты окончания предыдущего шага: Эти
варианты определяют состояние процесса. Например, при определении коли-
чества средств, вкладываемых в предприятие в
i
-м году, необходимо знать,
сколько средств осталось в наличии к этому году и какая прибыль получена в
предыдущем (
1
−
i
)-м
году. Таким образом, при выборе шагового управления
необходимо учитывать: 1) возможные исходы предыдущего шага и 2) влияние
управления на все оставшиеся до конца процесса шаги.
В задачах динамического программирования первый пункт учитывают,
делая на каждом шаге условные предположения о возможных вариантах окон-
чания предыдущего шага и проводя для каждого из вариантов условную опти-
мизацию. Выполнение второго пункта обеспечивается тем, что в задачах ди-
намического программирования условная оптимизация проводится от конца
процесса к началу. Сперва оптимизируется последний
m
-й шаг, на котором не
надо учитывать возможные воздействия выбранного управления
m
x
на все по-
следующие шага, так как эти шаги просто отсутствуют. Делая предположения
об условиях окончания (
1
−
m
)-гo шага, для каждого из них проводят условную
оптимизацию
m
-го шага и определяют условное оптимальное управление
m
x
.
Аналогично поступают для (
1
−
m
)-го шага, делая предположения об исходах
окончания (
2
−
m
)-го шага и определяя условное оптимальное управление на
(
1
−
m
)-м шаге, приносящее оптимальный выигрыш на двух последних шагах –
(
1
−
m
)-м и
m
-м. Так же действуют на всех остальных шагах до первого. На
первом шаге, как правило, не надо делать условных предположений, так как
состояние системы перед первым шагом обычно известно.

79
Для этого состояния выбирают оптимальное шаговое управление,
обеспечивающее оптимальный выигрыш на первом и всех последующих ша-
гах. Это управление является безусловным оптимальным управлением на пер-
вом шаге и, зная его, определяются оптимальное значение выигрыша и безус-
ловные оптимальные управления на всех шагах. Ниже это будет пояснено на
примерах.
5.2. Составление математической модели динамического програм-
мирования
Дополнительно введем следующие условные обозначения:
s
– состояние процесса;
i
S
– множество возможных состояний процесса перед
i
-м шагом;
i
W
– выигрыш с
i
-го шага до конца процесса,
mi ,1=
.
Можно определить следующие основные этапы составления математи-
ческой модели задачи динамического программирования.
1. Разбиение задачи на шаги (этапы). Шаг не должен быть слишком
мелким, чтобы не проводить лишних расчетов и не должен быть слишком
большим, усложняющим процесс шаговой оптимизации.
2. Выбор переменных, характеризующих состояние
s
моделируемого
процесса перед каждым шагом, и выявление налагаемых на них ограничений.
В качестве таких переменных следует брать факторы, представляющие инте-
рес для исследователя, например годовую прибыль при планировании дея-
тельности предприятия.
3. Определение множества шаговых управлений
i
x
,
mi ,1=
и налагае-
мых на них ограничений, т.е. области допустимых управлений X.
4. Определение выигрыша
),(
iii
xs
ϕ
(5.2.1)
который принесет на
i
-м шаге управление
i
x
, если система перед этим
находилась в состоянии s.
5. Определение состояния
's
, в которое переходит система из состоя-
ния s под влиянием управления
i
x
,
),('
ii
xsfs =
(5.2.2)
где
i
f
– функция перехода на
i
-м шаге из состояния s в состояние
's
.
6. Составление уравнения, определяющего условный оптимальный вы-
игрыш на последнем шаге, для состояния s моделируемого процесса
)},({)(
max
mm
XX
m
xsSW
m
ϕ
∈
=
(5.2.3)
7. Составление основного функционального уравнения динамическо-
го программирования, определяющего условный оптимальный выигрыш для
данного состояния s с
i
-гo шага и до конца процесса через уже известный ус-
ловный оптимальный выигрыш с (
1
+
i
)-го шага до конца:

80
))},((),({)(
1
max
iiiim
XX
i
xsfWxsSW
m
+
∈
+=
ϕ
(5.2.4)
В уравнении (5.2.4) в уже известную функцию
)(
1
sW
i
+
, характеризую-
щую условный оптимальный выигрыш с (
1
+
i
)-го шага до конца процесса,
вместо состояния s подставлено новое состояние
),('
ii
xsfs =
в которое система
переходит на
i
-м шаге под влиянием управления
i
x
.
Заметим, что структура модели динамического программирования от-
личается от статической модели линейного программирования. Действитель-
но, в моделях линейного программирования управляющие переменные – это
одновременно и переменные состояния моделируемого процесса, а в динами-
ческих моделях отдельно вводятся переменные управления
i
x
, и переменные,
характеризующие изменение состояния s под влиянием управления. Таким об-
разом, структура динамических моделей более сложная, что естественно, так
как в этих моделях дополнительно учитывается фактор времени.
5.3.Этапы решения задачи динамического программирования
После того как выполнены пункты 1–7, изложенные в предыдущем па-
раграфе, и математическая модель составлена, приступают к ее расчету. Ука-
жем основные этапы решения задачи динамического программирования.
1. Определение множества возможных состояний
m
S
для последнего
шага.
2. Проведение условной оптимизации для каждого состояния
m
Ss ∈
на
последнем
m
-м шаге по формуле (5.2.3) и определение условного оптимально-
го управления
)(sx
,
m
Ss ∈
3. Определение множества возможных состояний
i
S
для
i
-го шага,
1,...,3,2
−
=
mi
.
4. Проведение условной оптимизации
i
-го шага,
1,...,3,2
−
=
mi
для каж-
дого состояния
i
Ss ∈
по формуле (5.2.4) и определение условного оптимально-
го управления
)(sx
i
,
i
Ss ∈
,
1,...,3,2
−
=
mi
.
5. Определение начального состояния системы
1
s
, оптимального выиг-
рыша
)(
11
SW
и оптимального управления
)(
11
Sx
по формуле (5.2.4) при
i
=1.
Это есть оптимальный выигрыш для всей задачи
*)(*
11
xWW =
.
6. Проведение безусловной оптимизации управления. Для проведения
безусловной оптимизации необходимо найденное на первом шаге оптималь-
ное управление
)(*
111
sxx =
подставить в формулу (5.2.2) и определить следую-
щее состояние системы
),(
1122
xsfs =
. Для измененного состояния найти опти-
мальное управление
)(*
222
sxx =
, подставить в формулу (5.2.2.) и т.д. Для
i
-гo
состояния
i
s
найти
*),(
11 iiii
xsfs
++
=
и
)(
11
++
ii
sx
и т.д.
