Патудин В.М., Блем А.Г. Математическая экономика

Подождите немного. Документ загружается.

Задача о назначениях

В общем виде задача о назначениях формулируется следующим обра-

зом.

Имеется

работ и

кандидатов для их выполнения. Затраты

-го кан-

дидата на выполнение

-й работы равны

),1,(

njic

. Каждый кандидат может

быть назначен только на одну работу, и каждая работа может быть выполнена

только одним кандидатом. Требуется найти назначение кандидатов на работы,

при котором суммарные затраты на выполнение работ минимальны.

Запишем формально данную задачу. Пусть

– переменная, значение

которой равно 1, если

-й кандидат выполняет

-ю работу, и 0 – в противном

случае. Тогда условие о том, что каждый кандидат выполняет только одну ра-

боту, запишется в виде

∑

njx

,1,1

Условие о том, что каждая работа может выполняться одним кандида-

том, запишется в виде

∑

nix

,1,1

Целевая функция задачи имеет вид

∑∑

ijij

xсС

В функцию входят только те значения

(

ni ,1=

;

nj ,1=

), для которых

отличны от 0, т.е. входят затраты, соответствующие назначенным работам.

Математическая модель выглядит следующим образом:

min

→=

∑∑

ijij

xсС

(3.5.1)











==∈

∑

njmix

njx

mix

,1,,1},1,0{

;,1,1

(3.5.2)(3.5.3)(3.5.4)

Решить задачу о назначениях – значит найти

, удовлетворяющие

(3.5.2) – (3.5.4) и доставляющие минимум функции (3.5.1). Задача (3.5.1) –

(3.5.4) является, очевидно, задачей линейного программирования (целевая

функция линейна, ограничения линейны) и может быть решена симплекс-

методом. Также задача (3.5.1) – (3.5.4) – это транспортная задача, в которой

правые части ограничений равны 1, а переменные могут принимать только

два значения. Однако относительно простая форма задачи позволила разрабо-

тать для ее решения достаточно простые методы, один из которых – венгер-

ский.

3.6. Венгерский метод решения задачи о назначениях

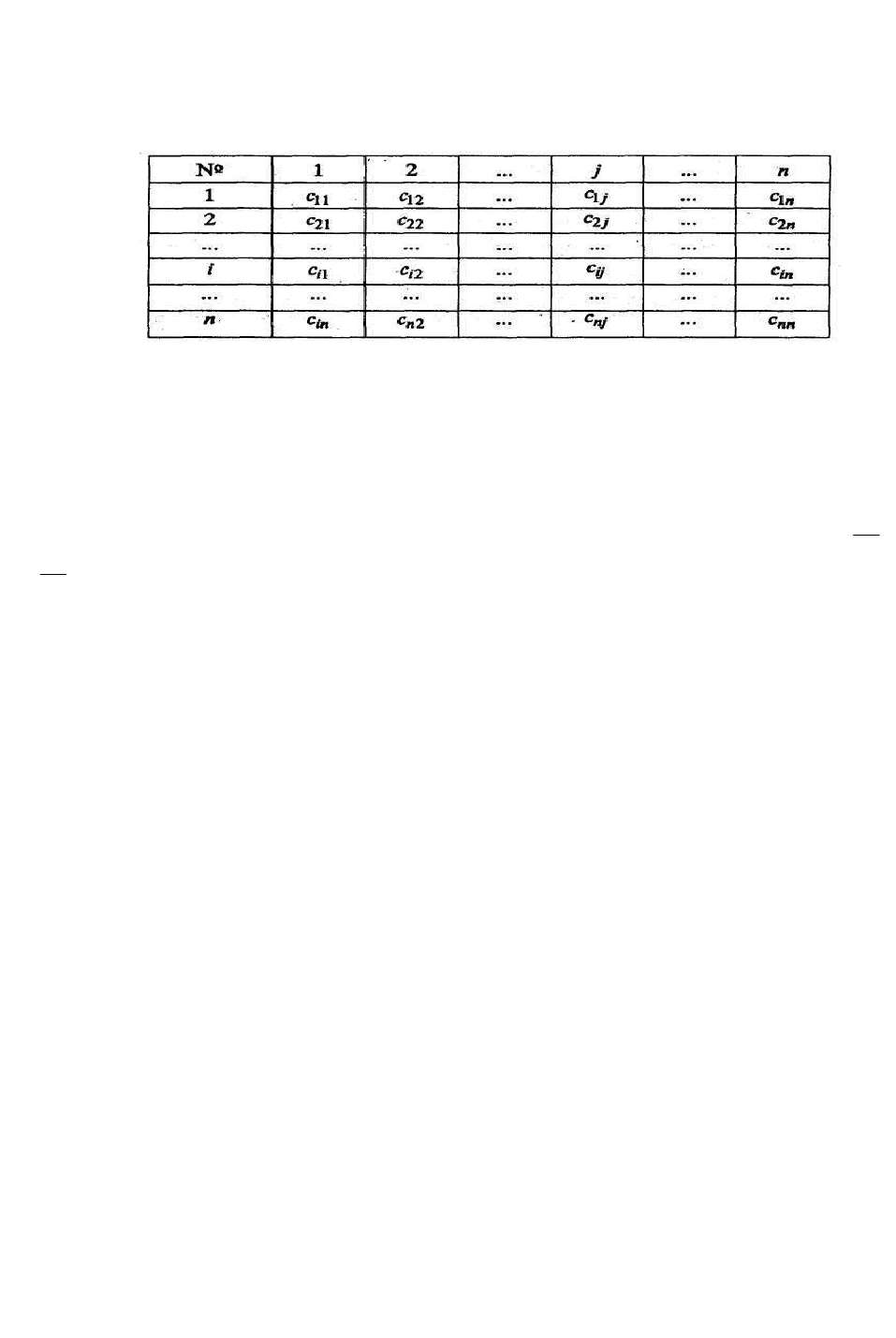
Для решения задачи о назначениях составляют таблицу (табл. 3.6.1):

Таблица 3.6.1

В левой колонке записаны номера кандидатов, в верхней строке – но-

мера работ. В

-й строке

-м столбце стоят затраты на выполнение

-м канди-

датом

-й работы.

В венгерском методе используется следующий принцип: оптималь-

ность решения задачи о назначениях не нарушается при уменьшении (увели-

чении) элементов строки (столбца) на одну и ту же величину. Решение счита-

ется оптимальным, если все измененные таким образом затраты

0≥

, (

ni ,1=

;

nj ,1=

) и можно отыскать такой набор

, что

∑∑

ijij

xс

Алгоритм метода содержит следующие шаги.

Шаг 1. Получение нулей в каждой сроке. Для этого в каждой строке

определяют наименьший элемент, и его значение отнимают от всех элементов

этой строки. Переход к шагу 2.

Шаг 2. Получение нулей в каждом столбце. В преобразованной табли-

це в каждом столбце определяют минимальный элемент, и его значение вычи-

тают из всех элементов этого столбца. Переход к шагу 3.

Шаг 3. Поиск оптимального решения. Просматривают строку, содер-

жащую наименьшее число нулей. Отмечают один из нулей этой строки и за-

черкивают все остальные нули этой строки и того столбца, в котором находит-

ся отмеченный нуль. Аналогичные операции последовательно проводят для

всех строк. Если назначение, которое получено при всех отмеченных нулях,

является полным (т.е. число отмеченных нулей равно

), то решение является

оптимальным, в противном случае следует переходить к шагу 4.

Шаг 4. Поиск минимального набора строк и столбцов, содержащих все

нули.

Для этого необходимо отметить:

1) все строки, в которых не имеется ни одного отмеченного нуля;

2) все столбцы, содержащие перечеркнутый нуль хотя бы в одной из

отмеченных строк;

3) все строки, содержащие отмеченные нули хотя бы в одном из отме-

ченных столбцов.

Действия 2) и 3) повторяются поочередно до тех пор, пока есть что от-

мечать. После этого необходимо зачеркнуть каждую непомеченную строку и

каждый помеченный столбец.

Цель этого шага – провести минимальное число горизонтальных и вер-

тикальных прямых, пересекающих по крайней мере один раз все нули.

Шаг 5. Перестановка некоторых нулей.

Взять наименьшее число из тех клеток, через которые проведены пря-

мые. Вычесть его из каждого числа, стоящего в невычеркнутых столбцах и

прибавить к каждому числу, стоящему в вычеркнутых строках. Эта операция

не изменяет оптимального решения, после чего весь цикл расчета повторить,

начиная с шага 3.

Пример 3.7.1

Институт получил гранты на выполнение четырех исследовательских

проектов. Выходные результаты первого проекта являются входными данны-

ми для второго проекта, выходные результаты второго проекта — это входные

данные для третьего проекта, результаты третьего проекта используются для

работы над четвертым проектом. В качестве научных руководителей проектов

рассматриваются кандидатуры четырех ученых, обладающих различным опы-

том и способностями. Каждый ученый оценил время, необходимое ему для

реализации проекта.

Матрица времен приведена ниже













8379

8274

5442

8573

-й строке

-м столбце матрицы

стоит время на выполнение

-м

ученым

-го проекта.

Продолжительность времени задана в месяцах. Требуется выбрать на-

учного руководителя для выполнения каждого проекта так, чтобы суммарное

время выполнения всех проектов было минимальным.

Решение.

Данная задача, очевидно, является задачей о назначениях. В качестве

работ рассматриваются исследовательские проекты, в качестве кандидатов –

ученые, претендующие на роль научных руководителей.

Введем переменные

случаепртивномв

проектагоjльруководитенаучныйученыййiесли

,1 −−−

Целевая функция задачи имеет вид

min83798274

54428573

4443424134333231

2423222114131211

→++++++++

xxxxxxxx

xxxxxxxxС

Решим задачу венгерским методом, используя приведенную ниже таб-

лицу. В

-й строке

-м столбце этой таблицы стоит время

на выполнение

го проекта

-м ученым,

ni ,1=

;

nj ,1=

. Выберем в каждой строке минимальный

элемент и запишем его в правом столбце табл. 3.6.2.

Таблица 3.6.2

Вычтем минимальные элементы из соответствующих строк, перейдем

к новой таблице, в которой найдем минимальные значения в каждом столбце и

запишем их в нижней строке табл. 3.6.3.

Таблица 3.6.3

Отнимем минимальные элементы из соответствующих столбцов. Пе-

рейдем к табл. 3.6.4.

Таблица 3.6.4

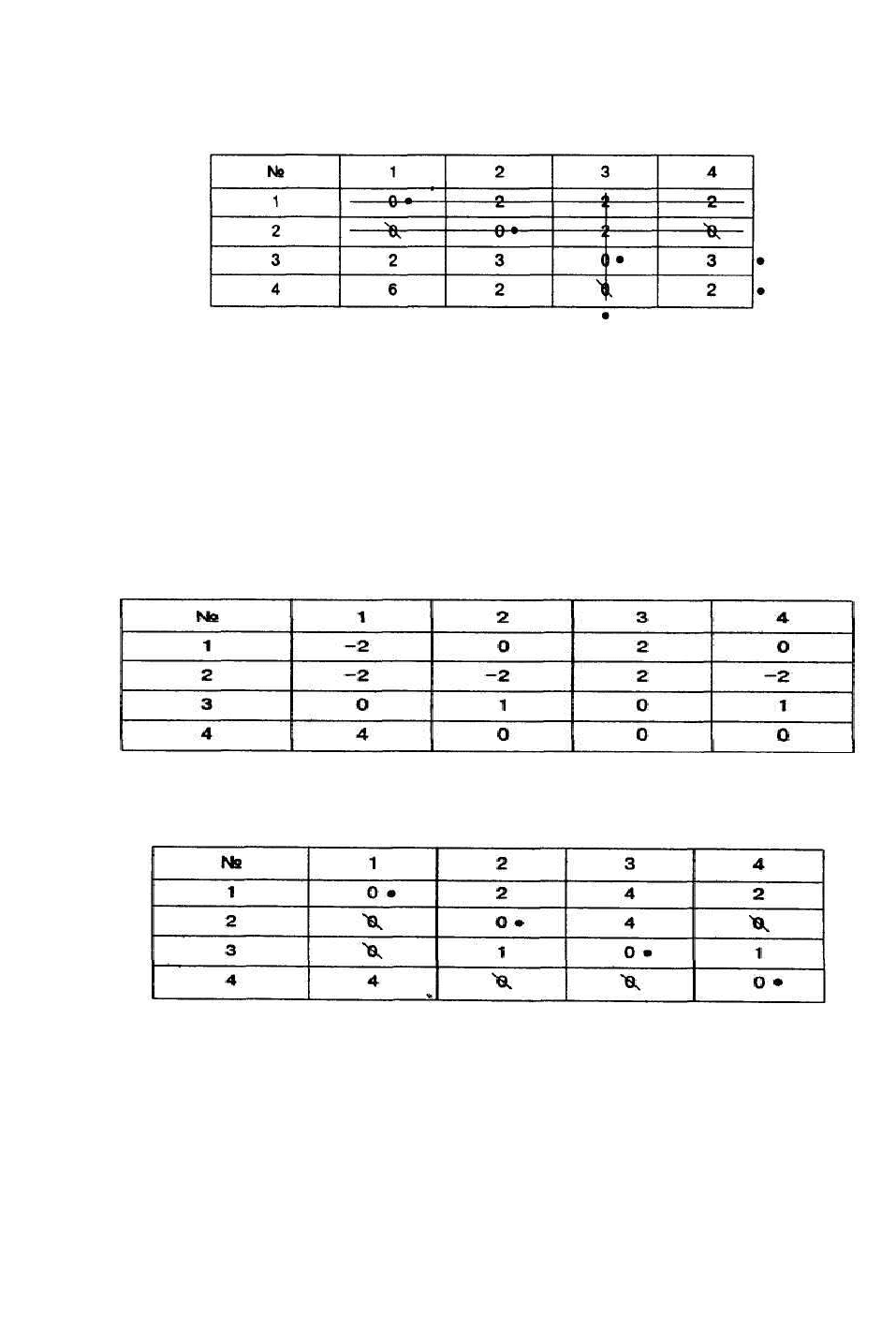
В табл. 3.6.4 сделаем назначения. Строками, содержащими наименьшее

число нулей (один нуль), являются первая, третья и четвертая строки. Отметим

точкой 0 первой строки. Вычеркнем 0 из первого столбца. Это вычеркивание

означает, что так как первый ученый назначен научным руководителем перво-

го проекта, второй ученый уже не может быть назначен. Отмечаем 0 в третьей

строке и вычеркиваем 0, стоящий в четвертой строке в третьем столбце, что

соответствует тому, что четвертый ученый уже не может быть назначен науч-

ным руководителем третьего проекта.

Отмечаем любой из нулей второй строки (действуя по порядку, отме-

чаем нуль, стоящий во втором столбце) и вычеркиваем нуль, стоящий в чет-

вертом столбце. Это вычеркивание означает, что так как второй ученый назна-

чен научным руководителем второго проекта, то он не может быть выбран для

выполнения четвертого проекта.

Число отмеченных нулей равно 3, т.е. назначение не является полным.

Перейдем к шагу 4 алгоритма.

Найдем минимальный набор строк и столбцов, содержащий все нули

(табл. 3.6.5).

Таблица 3.6.5

Отметим точкой четвертую строку, не содержащую ни одного отме-

ченного нуля. Отметим третий столбец, содержащий перечеркнутый нуль в

четвертой строке. Отметим третью строку, содержащую отмеченный нуль в

третьем столбце. Кроме третьего столбца, больше нет столбцов, содержащих

перечеркнутые нули в отмеченных строках. Вычеркнем отмеченный столбец и

неотмеченные строки. В оставшихся клетках минимальный элемент равен 2.

Вычтем его из каждого числа невычеркнутых (1,2,4) столбцов. Получим табл.

3.6.6.

Таблица 3.6.6

Теперь прибавим 2 к каждому числу вычеркнутых строк в преобразо-

ванной таблице. Получим табл. 3.6.7.

Таблица 3.6.7

Вновь сделаем назначение, отметив по порядку нули в табл. 3.6.7.

Это назначение является полным, так как число отмеченных нулей

равно 4. Получено следующее назначение:

− первый ученый назначается научным руководителем первого про-

екта:

;

− второй ученый – научный руководитель второго проекта:

;

− третий ученый – научный руководитель третьего проекта:

;

− четвертый ученый – научный руководитель четвертого проекта:

Время выполнения четырех проектов: С=3+4+2+8 =17.

Данное назначение не единственное. Если во второй строке сначала

отметить не второй, а четвертый нуль, получим следующее назначение (табл.

3.6.8):

Таблица 3.6.8

− первый ученый руководит первым проектом:

;

− второй ученый руководит четвертым проектом:

;

− третий ученый руководит третьим проектом:

;

− четвертый ученый руководит вторым проектом:

Время на выполнение проектов не изменилось:

С=3*1+5*1+2*1+7*1=17

Таким образом, получены два оптимальных назначения, которым соот-

ветствует минимальное время выполнения. Заметим, что результат, получен-

ный по венгерскому методу, не изменится, если в алгоритме заменить строки

на столбцы, и наоборот.

3.7. Применение задачи о назначениях к решению экономических

проблем

Выше уже был дан пример применения задачи о назначениях к про-

блеме оптимального выбора руководителей исследовательских проектов. При-

ведем еще несколько примеров, когда использование задачи о назначениях по-

зволяет найти оптимальное решение экономической задачи.

Оптимальное исследование рынка

Группе, исследующей рынок, требуется получить данные из

различ-

ных мест. В ее распоряжении имеется

дней, и она предполагает провести по

одному дню в каждом месте, проведя по

опросов,

nj ,1=

. Вероятность ус-

пешного опроса в каждом месте задается матрицей

. Элемент матрицы

характеризует вероятности успешного опроса в течение

-го дня в

-м месте,

ni ,1=

;

nj ,1=

Определить время проведения опросов, при котором общее число оп-

росов максимально.

Решение

Сведем данную задачу к задаче о назначениях.

Введем величину

jijij

apr −=

, показывающую число успешных опросов

-м месте в течение

-го дня.

случаепротивномв

местемjвпроводитсяопросденьйiвесли

,1 −−

Математическая модель задачи имеет следующий вид:

max

→=

∑∑

ijij

xrR











==∈

∑

njnix

njx

nix

,1,,1},1,0{

;,1,1

Функция

характеризует суммарное число опросов. Его нужно мак-

симизировать. Первое и второе ограничения соответствуют тому, что в тече-

ние одного дня можно находиться только в одном месте. Для расчета модели

венгерским методом надо перейти к противоположной функции

∑∑

−=

ijij

xrR

и в соответствующей таблице записывать значения

с противопо-

ложным знаком.

Оптимальное использование торговых агентов

Торговая фирма продает товары в

различных городах, покупатель-

ная способность жителей которых оценивается в

усл. ед.,

nj ,1=

. Для реали-

зации товаров фирма располагает

торговыми агентами, каждого из которых

она направляет в один из городов. Профессиональный уровень агентов разли-

чен; доля реализуемых

-м торговым агентом покупательных способностей

составляет

ni ,1=

. Как следует распределить торговых агентов по городам,

чтобы фирма получила максимальную выручку от продажи товаров?

Решение.

Оптимальное решение этой проблемы может быть найдено с помощью

задачи о назначениях. В качестве кандидатов выступают торговые агенты, в

качестве работ – города.

Введем параметр

jiij

bac =

, характеризующий величину покупательных

способностей, реализуемых

-м торговым агентом в

-м городе.

Управляющие переменные

ni ,1=

nj ,1=

определяются по формуле

случаепротивномв

городйjвнаправленагентйiесли

,1 −−

Математическая модель запишется в следующей форме:

max

→=

∑∑

ijij

xсС











==∈

∑

njnix

njx

nix

,1,,1},1,0{

;,1,1

Первое и второе ограничения формализуют соответственно условия о

том, что в каждый город направляется один торговый агент, и один торговый

агент не может работать в двух городах. Целевая функция С – это сумма реа-

лизованных покупательных способностей всеми торговыми агентами во всех

городах. Она должна быть максимальна. Для решения задачи венгерским ме-

тодом надо, как и в предыдущем примере, перейти к противоположной функ-

ции.

4. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

4.1. Постановка задачи нелинейного программирования

В общем виде задача нелинейного программирования (ЗНП) формули-

руется следующим образом:

max(min)),...,,(

→

xxxf

(4.1.1)











+==

+=≤

=≤

mmibxxxg

mibxxxg

ini

,2,),...,,(

;,1,),...,,(

..........................................

;,1,),...,,(

221

121

(4.1.2)

где

– управляющие переменные или решения ЗНП,

nj ,1=

;

– фиксированные параметры,

mi ,1=

;

ni ,1=

– заданные функции от

переменных.

Если

линейны, то (4.1.1), (4.1.2) переходит в задачу линейного

программирования.

Решить задачу нелинейного программирования – это значит найти та-

кие значения управляющих переменных

nj ,1=

, которые удовлетворяют

системе ограничений (4.1.2) и доставляют максимум или минимум функции

Для задачи нелинейного программирования, в отличие от линейных

задач, нет единого метода решения. В зависимости от вида целевой функции

(4.1.1) и ограничений (4.1.2) разработано несколько специальных методов ре-

шения, к которым относятся методы множителей Лагранжа, квадратичное и

выпуклое программирование, градиентные методы, ряд приближенных мето-

дов решения, графический метод.

Заметим, что нелинейное моделирование экономических задач часто

бывает довольно искусственным. Большая часть экономических проблем сво-

дится к линейным моделям, поэтому в данном пособии нелинейные модели и

методы расчета рассмотрены достаточно кратко.

4.2 Геометрическая интерпретация задачи нелинейного програм-

мирования. Графический метод решения

Рассмотрим задачу Нелинейного программирования, содержащую две

переменные.

max(min)),(

→xxf

(4.2.1)











+==

+=≤

=≤

mmibxxg

mibxxg

,2,),(

;,1,),(

221

121

(4.2.2)

Система ограничений (4.2.2) определяет в

-мерном пространстве не-

которую область, которая является областью допустимых решений задачи.

Решить ЗНП графически – это значит найти точку области допустимых

решений (4.2.2), через которую проходит линия

Cxxf =),(

наивысшего (наи-

низшего) уровня.

Указанная точка может находиться как на границе, так и внутри облас-

ти допустимых решений (4.2.2), в отличие от задач линейного программирова-

ния.

Так же, как и для линейных задач, ЗНП удобно решать графически, ко-

гда функция и ограничения содержат две переменные.

Алгоритм решения ЗНП графическим методом

Шаг 1. На плоскости

0xx

строят область допустимых решений, опре-

деленную ограничениями (4.2.2). Если она пуста, т.е. ограничения несовмест-

ны, то задача (4.2.1) – (4.2.2) не имеет решения. В противном случае переходят

к шагу 2.

Шаг 2. Строят линию уровня функции

Cxxf =),(

, где С – некоторая

константа. Переход к шагу 3.

Шаг 3. Определяют направление возрастания (при максимизации),

убывания (при минимизации) функции

Шаг 4. Находят точку области допустимых решений, через которую

проходит линия уровня

Cxxf =),(

с наибольшим (при максимизации), наи-

меньшим (при минимизации) значением С или устанавливают неограничен-

ность функции на области допустимых решений.

Шаг 5. Определяют значения

, xx

для точки, найденной на шаге 4, и

величину функции

в этой точке.

Пример 4.2.1

max(min)32

→+= xxf











≥

≤+

≥

;16

;3,

В соответствии с алгоритмом построим на плоскости

0xx

область до-

пустимых решений (рис. 4.2.1)