Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

6.2 Modeling of Preparation Processes for BSCCO/Ag Tapes 289

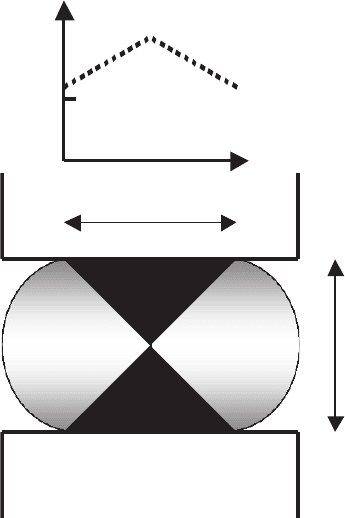
Fig. 6.10. Inhomogeneous deformation under compression (Y is the yield value of

the sample). The shaded regions have experienced less deformation than the remain-

der of the slab

is small, then the required pressure to induce plastic ﬂow in the material is

high, and vice versa. This means that the material has a large freedom to

ﬂow, which is found by the freedom parameter, Δ

= h/L.

Pressing. The freedom parameter, Δ

, can be used to describe how freely

the material expands. During plane pressing, the larger the Δ

,thelargerthe

expansion. Therefore, the width increase of a narrow thick tape is larger that

that of a wide thin tape under the same pressure. The values of Δ

will be

diﬀerent if the contact sizes are not the same in the x-andy-directions. For

example, if the contact size in the x-direction is shorter than the contact size

in the y-direction, then the expansion in the x-direction will be larger than

that in the y-direction.

Rolling. Fig. 6.11 presents the ﬂat rolling process. Due to the friction at

the interface between the rollers and sample, a friction hill is built up during

rolling. Lubrication can reduce the constraint and therefore also reduce the

stress in the sample, when other rolling parameters are ﬁxed. If the sample

height is much smaller than the roller diameter, (6.49) could be used as a

rough estimation with the mean height h:

h =(h

+ h

)/2 , (6.50)

290 6 Modeling of BSCCO Systems and Composites

Fig. 6.11. Illustration of the ﬂat rolling process

where h

and h

are the original and ﬁnal heights of the sample, respectively.

The contact size in the sample length direction, L

,isgivenas

≈



R(h

− h

√

Rδh , (6.51)

where R is the roller radius and δh is the height reduction of the sample [441].

If a tensile stress, σ

, is applied to the sample during rolling, then (6.49) gives

=(2k − σ

)





. (6.52)

This means that the rolling pressure and therefore the stress in the sample

could be decreased, applying a tensile stress during rolling.

The freedom parameter in the sample length direction, Δ

f,L

= h/L

√

Rδh, depends on the roller radius, sample height and the height decreasing.

For example, the rolling of a thick tape, using larger rollers, could be similar to

that of a thin tape, using small rollers. The freedom parameter in the sample

width direction is given by Δ

f,w

= h/L

,whereL

is the width of the sample.

The ratio between the freedom parameters, Δ

f,L

/Δ

f,w

= L

√

Rδh,isuseful

to determine the direction in which the material is most apt to deform. In

particular, large rollers, a large decreasing and a small tape width could lead

to a signiﬁcant width increase during rolling and vice versa.

Drawing and extrusion are axis-symmetric deformation processes (see

Fig. 6.12), which are in principle similar. There are two main diﬀerences be-

tween them, namely (i) the compressive stress in the deformation zone during

extrusion is larger than that of drawing, especially because the area decreasing

during extrusion is often much larger than the decrease in a drawing process

;

(ii) there is a tensile stress in the exiting wire during drawing, which limits the

This means that the powder density in a BSCCO/Ag composite is larger after

extrusion than after drawing.

6.2 Modeling of Preparation Processes for BSCCO/Ag Tapes 291

Fig. 6.12. Illustration of the drawing and extrusion process

maximum drawing force and the maximum decrease by the strength of the

material. The fact that it is possible to obtain very large decreasing ratios in

the extrusion process makes it an eﬃcient process for large-scale production.

However, it is rather diﬃcult to obtain homogeneous Bi-2223/Ag composites

by extrusion [458].

The freedom parameter, Δ

= h/L, could be determined using (6.50) and

the contact size, L,as

L =

− h

2sinα

δh

2sinα

, (6.53)

where h

and h

is the original and ﬁnal diameters of the sample, respectively,

δh is the diameter decreasing and α is the half-angle of the die.

Thus, the diﬀerent constraint factors have a strong inﬂuence on the defor-

mation process. By introducing the freedom parameter, Δ

,itispossibleto

estimate these eﬀects using only one parameter. Table 6.1 gives a summary of

the expression of the freedom parameters for various deformation processes.

Table 6.1. Freedom parameters for various deformation processes

Pressing Rolling Drawing or extrusion

= h/L

f,L

= h/

√

Rδh

f,w

= h/L

δh

sin α

It should be noted that the condition of drawing or extrusion is usually far from

that of plane pressing. However, the concept of the freedom parameter could be

useful for qualitative estimations. For example, the stress in the sample will be

large if the die angle is small or the diameter decreasing is large or the diameter

of the sample is small.

292 6 Modeling of BSCCO Systems and Composites

The presented description of the mechanical deformation process is only

for single-element samples. The duplex systems, such as BSCCO/Ag compos-

ites, are needed in additional considerations. The diﬀerence of the mechanical

properties of each component leads to diﬀerent behavior of the mass ﬂow of

each component during deformation, resulting in a “mass re-distribution.” As

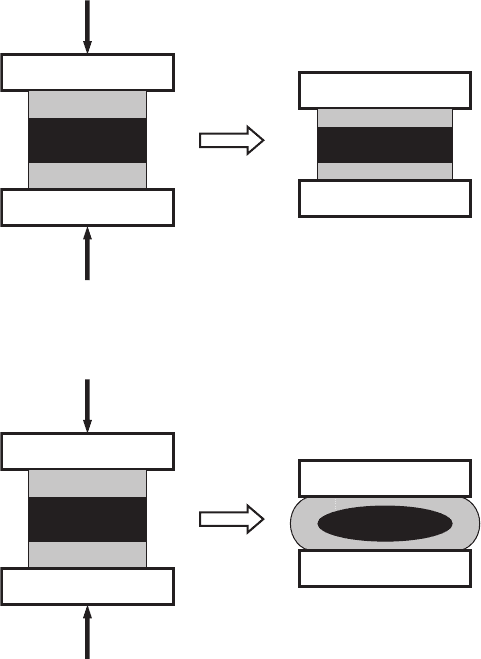
shown in Fig. 6.13 the deformation of a weaker component will be larger than

that of a stronger one. A weak component is deﬁned by a lower yield stress

or a diﬀerent ﬂow behavior. This leads to the symmetry change of the com-

ponent mass distribution for the composites and could be the main reason for

the inhomogeneity introduced when BSCCO/Ag composites are mechanically

(b)

(a)

Fig. 6.13. Mass re-distribution during pressing: (a) homogeneous deformation at

equivalent mechanical properties of both components, and (b) inhomogeneous de-

formation, causing the mass re-distribution (the dark area represents a stronger

component)

6.2 Modeling of Preparation Processes for BSCCO/Ag Tapes 293

deformed. A lightened deformation of a weak component leads to convey a

high pressure to the strong component under certain constraint conditions

(see Fig. 6.13b). Due to the friction at the interfaces between the anvils and

the sample, between weak and strong components, a high stress could be built

up in the center region of the weak parts, especially when the height of the

sample is much smaller than the width of the sample, that is, the freedom pa-

rameter is small. This leads to transport of pressure through the weak region

to the strong part of the sandwich. At the edges of the sandwich, the weak

component is less constrained and can transport less direct pressure to the

strong part. However, the shear stresses might still be considerable, deﬁning

deformation at the edges of the strong part. Obviously, constraint conditions

or the freedom parameter have a strong inﬂuence on the mass re-distribution

process.

If the density of the superconductor is not very high, then the BSCCO/Ag

core can be considered as the weaker part of the composite, resulting in a more

signiﬁcant deformation of the core than with the silver sheath. On the other

hand, if the core density is very high, then the Ag sheath could be the weaker

component unable to convey high enough pressure to the core for further

densiﬁcation of the core. However, by lowering the freedom parameter of the

process (Δ

f,L

= h/

√

Rδh), the mass-ﬂow behavior could be changed so that

the Ag sheath could again transport a high enough pressure to increase the

density of the superconductor, although the silver part is still the weaker

component of the composite. Obviously, when the roller diameter is larger

than the wire diameter, the freedom parameter is small, deﬁning larger mass

re-distribution.

The freedom parameter also has inﬂuence on the sausaging. If the freedom

parameter is large, the mass ﬂow of the Ag sheath is large, and the sausaging

(at least the sausaging frequency) as well as the density of the core will be

decreased. The freedom parameter at rolling (Δ

f,L

= h/

√

Rδh) assumes that

sausaging could be decreased, using small rollers, which has been supported

by test results [568]. This also implies that sausaging will be more pronounced

when the thickness of the tape becomes small; this has also been demonstrated

[568]. It should be pointed that the smaller factor of thickness decreasing

causes the larger freedom of silver sheath in the direction of the wire length.

Therefore, it is not surprising that the BSCCO core density, obtained in this

way, is smaller than the core density obtained, using a larger decreasing factor.

Compatibility line

The stresses developed in a material due to an external loading can be es-

timated using the so-called Mohr circles [715]. The intrinsic curve, giving

the behavior of a material for a given deformation ε, is obtained by draw-

ing the envelope of these Mohr circles. In particular, Fig. 6.14a shows the

intrinsic curves for Bi-2223 and Ag at a deformation ε = 25%. The existence

of this intersection (P

) is called the compatibility point. Its existence shows

294 6 Modeling of BSCCO Systems and Composites

(τ, σ, ε)

–1400

Normal Stress, σ (MPa)

Bi-2223

600

400

200

Shear Stress, (MPa)

(a)

600

400

200

(b)

15%

25%

50%

60%

Shear Stress, τ(MPa)

–1000 –600 –200 0

Bi-2223

–1000 –800 –600 –400 –200 0

Normal Stress, σ (MPa)

Fig. 6.14. (a) Determination of the compatibility point P

(σ, τ, ε =25%)atthe

intersection of the intrinsic curves for a Bi-2223 ceramic and metallic Ag; (b)the

compatibility line between Bi-2223 and Ag: trace of the compatibility points P

ε varies from 5 to 60%. S

corresponds to the plasticity threshold of the Bi-2223

ceramic and S

to the compatibility threshold before the brittle fracture between

the Bi-2223 ceramic and metallic Ag [766]

that in spite of quite diﬀerent mechanical behavior at atmospheric pressure of

the matrix and ﬁlaments, there are external mechanical stresses deﬁning the

same ductile behaviors of silver and superconductor. By drawing such intrin-

sic curves for diﬀerent deformation rates, one can obtain the line along which

moves, called the compatibility line. One corresponds to conditions where

the superconducting powder and the sheath both have the same mechani-

cal behavior, especially in the ductile domain. Then, instead of fabricating

6.2 Modeling of Preparation Processes for BSCCO/Ag Tapes 295

wires at atmospheric pressure, that is, out of the plastic domain for the

superconducting powder (S

limit, see Fig. 6.14b) and out of the ductile zone

common to the powder and to the sheath (S

limit, see 6.14b), it is much

more expedient to use an analysis of triaxial stress state. This approach helps

to minimize Ag/BSCCO interface sausaging, using yielding criterion, deﬁning

the deformation compatibility of silver matrix and superconducting core [190].

6.2.4 Finite-Element Modeling of Deformation Processes

Rolling and Pressing of BSCCO/Ag Tapes

The ﬁnite element method (FEM) is capable of obtaining qualitative estima-

tions of parameters found by material deformation during BSCCO/Ag tape

processing. However, the FEM application to these problems is a complicated

task still not widely applied. For instance, the limiting factors for this method

are complicated geometry of the composite and great time required to obtain

numerical results with necessary accuracy. The application of coarse meshes

can decrease the simulation time. However, these meshes could lead to simu-

lation problems and insuﬃcient detailing of results.

In [660, 967, 1048], drawing of monocore wire is modeled by two-

dimensional axis-symmetric models. The constitutive equations describing the

powder ﬂow are stated using the Drucker-Prager model with an elliptical cap

criterion. Process parameters, such as the die angle and degree of reduction in

each drawing step, are shown to inﬂuence the density of the powder in drawn

wire. The distribution of density, being high at the silver/powder interface

and lower in the center, is in agreement with test data. FEM modeling of

the multi-ﬁlament wire drawing has not been found in literature, probably

because a full three-dimensional model is necessary.

Numerical simulation of ﬂat rolling also requires a 3D model to describe

the deformations in length, width and thickness directions. Simpliﬁed 2D sim-

ulation can be made, assuming zero deformation in either the width or the

length direction. Assuming zero width strain, the pressure distribution along

the roll gap is modeled in [238, 633, 939]. In this case, the pressure proﬁle

forms either a friction hill or a friction valley, depending on the roll diam-

eter and degree of thickness reduction. These parameters also inﬂuence the

shear strains in the strain zone. When material ﬂow in the cross-section is

analyzed in a 2D model, zero strain in the length direction must be assumed

[256]. This technique enables the prediction of ﬁlament geometry and density,

incorporating the inﬂuence of wire geometry and friction.

The input data for numerical properties are essential for the precision of

numerical results. Reference [375] presents an extensive investigation of the

mechanical properties of BSCCO powder. The powder is evaluated applying

a combination of fracture tests and triaxial strain tests. As a result, it is

concluded that the Drucker-Prager model is not capable of describing the

yield surface of BSCCO powder in detail. Reference [57] shows how the yield

296 6 Modeling of BSCCO Systems and Composites

surface can be determined by a few relatively simple tests combined with a

Drucker-Prager conical cap model. It is demonstrated that an FEM simulation

based on this approach gives a rather good prediction of the density in the

individual ﬁlaments for small reductions of tape thickness in a 2D model.

In more details three FEM approaches for simulation of ﬂat rolling are

considered below [257]. The next diﬀerent approaches are applied, namely (i)

2D pressing in a mesh with 50 × 50 elements, (ii) 3D pressing between non-

rotating rolls in a mesh with 17 × 26 × 60 elements (number of elements in

width, height and length, respectively) and (iii) full 3D rolling in the same

mesh as in the case of the 3D pressing. The superconducting ﬁlaments have

rectangular shape and lie in a square matrix of pure silver, surrounded by an

alloyed silver sheath. Both silver materials are described by Von Mises yield

criterion with the ﬂow stress parameters (σ = Cε

) given in Table 6.2. The

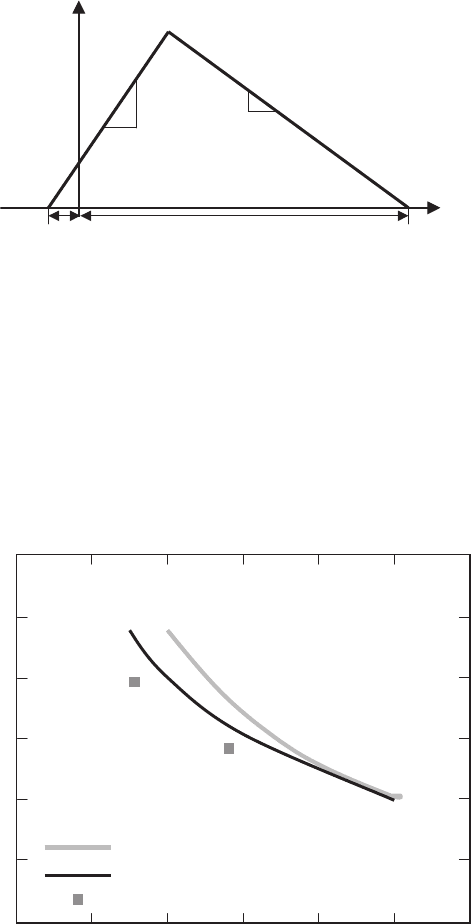
constitutive plasticity model, describing the powder, is the Drucker-Prager

model with a conical cap (see Fig. 6.15). This model is a rough approximation

to the real yield surface, but it includes the most important properties of

the powder, which are pressure-dependent yield stress, volumetric strain and

material hardening. In the



√



plane, the yield surface consists of two

intersecting lines, shown in Fig. 6.15. The Drucker-Prager failure surface is

written as



− η(p + p

)=0, (6.54)

where J

is the second invariant of the stress tensor, η is the slope of the

failure line and p

is the yield stress in pure, hydrostatic tension. The cap

yield surface is a line with a negative slope:



+ ξ(p − p

)=0, (6.55)

Table 6.2. The model parameters for silver, alloy and BSCCO powder

Parameters Silver Silver alloy BSCCO powder

Young’s modulus (MPa) 57.32 57.32 13.79

Poisson’s ratio 0.38 0.38 0.2

σ = Cε

C (MPa) 320 350 –

n 0.3 0.11 –

η –– 1.2

ξ – – 0.29

(MPa) – – 12

= a{exp[b(ρ − ρ

)] − 1}

a (MPa) – – 27

b––1

Relative density, ρ

–– 0.6

6.2 Modeling of Preparation Processes for BSCCO/Ag Tapes 297

1/2

Fig. 6.15. Drucker-Prager model with a conical cap [257]

where ξ is the slope of the cap line and p

is the hydrostatic compression yield

stress. The model parameters are given in Table 6.2 [375].

All three models calculate higher densities in the center than at the edges

and overestimate the relative density of ﬁlaments. In Fig. 6.16 the relation be-

tween tape thickness and tape width is shown for 2D and 3D FEM simulations

of rolling and pressing and compared with test data. As it is followed from

Fig. 6.16, the 3D rolling simulation ﬁts very well with the test results. At the

same time, the FEM simulations of both models overestimate the widening.

3.0

2.5

2.0

1.5

1.0

0.5

0.0

•

Rolling (Test, Rolls

with ∅ 85 mm)

2-D FEM (Pressing)

3-D FEM (Rolling )

3-D FEM (Pressing)

Tape Thickness (mm)

Tape Width (mm)

0 0.4 0.6 0.8 1.0 1.20.2

Fig. 6.16. Tape width vs tape thickness for experiments with ∅85 mm rolls and 2-D

and 3-D FEM simulations [257]

298 6 Modeling of BSCCO Systems and Composites

ThermalCyclingofBSCCO/AgTapes

FEM is also applied to investigate thermal cycling of BSCCO/Ag tapes. For

example, in [776], a simulation of thermal stresses is carried out in monocore

tape under the following assumptions:

– The BSCCO/Ag tape is stress-free at the sintering temperature (1113 K).

– The mechanical properties of both components are isotropic.

– Silver behaves elastically and plastically while BSCCO is brittle.

– The Baushinger eﬀect is neglected, that is, the magnitude of the yield

stress of silver is assumed to be the same in tension and compression.

– The composite is symmetrical about the x-andy-axes.

– The tape is inﬁnitely long so that plane strain conditions apply.

– The BSCCO core center is assumed to be 65% dense and the outer core is

assumed to be 85% dense.

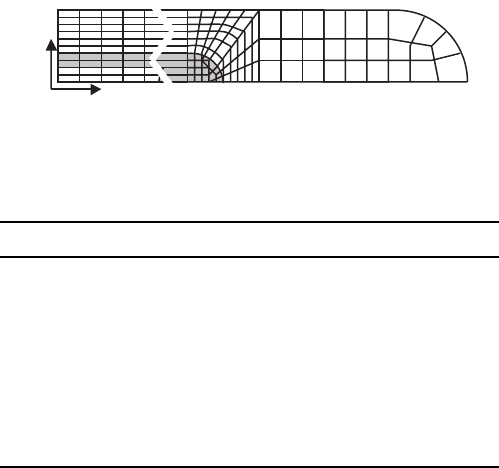
Figure 6.17 [776] shows a section of the mesh used for the thermal cycling

analysis. The x-axis is parallel to the width of the tape (3.5 mm), the y-axis

is parallel to the height of the tape (200 μm) and the z-axis is parallel to the

length, assuming to be inﬁnite. Both the central part of the core tape and

external part of the region corresponding to the silver sheath are presented by

white color. The gray part deﬁnes the external part of the superconductor or

interface. The mechanical properties of BSCCO and Ag are shown in Table 6.3,

Fig. 6.17. Mesh used for FEM computation. The entire mesh contains 1500 nodes

and 250 elements

Table 6.3. Mechanical properties of Ag and BSCCO [776]

Parameters BSCCO Ag

α(K

−1

)13.6 × 10

−6

21.9 × 10

−6

E (GPa), 100% dense 127.0 71.0

E (GPa), 85% dense 83.8 –

E (GPa), 65% dense 54.1 –

(MPa) at 300 K – 12.6

(GPa) at 300 K – 0.57

ν 0.14 0.37

(MPa) at 77 K – 13.2

(GPa)at77K – 0.7