Parinov I.A. Microstructure and Properties of High-Temperature Superconductors
Подождите немного. Документ загружается.

6.2 Modeling of Preparation Processes for BSCCO/Ag Tapes 299
30
25
20
15
10
5
0
–5
–10
300 K[1] 300 K[3] 77 K[3]
Width (mm)
σ
YY
(MPa)
0.0 0.3 0.5 0.8 1.0 1.3
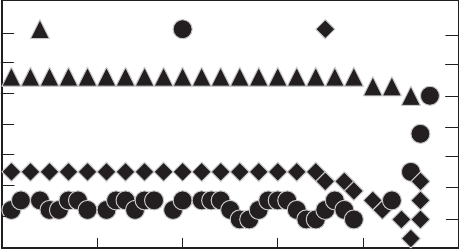
Fig. 6.18. FEM, showing the variation of σ
yy
with thermal cycling across the width
of BSCCO core. Cycles are denoted by the numbers in square brackets [776]
where E is Young’s modulus, ν is Poisson’s ratio, K
p
is the slope of the
stress–strain curve after yielding and σ
y
is the yield stress. Figure 6.18 shows
the variation of σ
yy
with thermal cycling across the width of the tape. The
stress state is fairly uniform in the center of the core except at the edges,
where the curvature of the core can act as a stress concentrator.

7
Modeling of YBCO Oxide Superconductors
7.1 Modeling of 123 Phase Solidification from Liquid
7.1.1 Heterogeneous Mechanism
Initially, for peritectic reaction (basis of melt processing), heterogeneous mech-
anism has been suggested, that is, a formation of 123 phase in direct contact
of melt and properitectic (“green”) 211 phase followed by the growth of 123
crystallites in account of the component diffusion through product layer [489].
Shortcoming of this mechanism results in the following causes:
(1) Calculated growth rate of 123 phase, limited by diffusion of slowest compo-
nent (D
Y
3+ = 10
−11
cm
2
/s), should be approximately 4 μm/h [54], which
is some order of magnitude less than test data [54, 890, 891]. In this case,
the peritectic reaction, which occurs in diffusion mechanism, should be
completed after formation of 123 layer around 211 particles.
(2) It is impossible to describe YBCO platelet structure, because diffusion of
components should mostly impede in the direction of dominant growth,
that is, in ab-plane.
(3) Parallel disposition of platelets is not explained, because arbitrary initial
orientation of particles of the 211 properitectic phase into liquid should
lead to the absence of anisotropy and to arbitrary orientation of 123 crys-
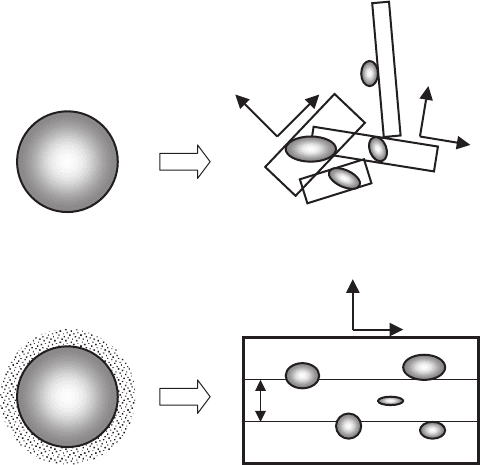
tallites, presented in Fig. 7.1a.
7.1.2 Models Based on Yttrium Diffusion in Liquid
In realization of melt-processing for preparation of YBCO large-granular sam-
ples with improved superconducting properties, it is important a priori to
obtain a grain growth in the direction of the gradient to maximize the ratio
of “external” thermal gradient (G) to solidification rate (R). From this point
of view, it seems better to transfer the sample across a large thermal gradi-
ent. However, in this case a large part of the sample stays for a long time at
elevated temperature, where Y
2
BaCuO
5
,BaCuO
2
and CuO
2
co-exist. More-
over, an undesirable change of the geometric shape of the sample is possible
302 7 Modeling of YBCO Oxide Superconductors
by liquid flow. Thus, a good compromise between G and R is required, be-
cause the G/R ratio governs the stability of the solidification process. The
thermodynamic aspects of this problem considered in [155, 475] have led to a
model of 211 phase solubility in liquid and homogeneous formation of nuclei
(see Fig. 7.1b). This model is based on the following assumptions:
(1) Ion concentration of Y
3+
attains a maximum in liquid near the surface
of 211 particle and decreases sharply at the mid-distance of neighbor 211
inclusions. When the distance exceeds this length, the ion concentration
of Y
3+
decreases asymptotically down to a value corresponding to the
peritectic melt.
(2) Increasing of yttrium concentration in the liquid enhances a possibility of
123 phase solidification because of metastability of the melt and existence
of figurative point in the two-phase region “123 solid phase–melt.”
(3) Constitutional undercooling in the system, leading to supersaturation of
the melt by yttrium, is found (i) by “external” thermal gradient, (ii) by
undercooling in comparison with saturated melt and (iii) by decreasing
of solidification temperature for melt, saturated by yttrium relatively to
peritectic melt.
211
Liquid
c
a
c
a
(a)
Liquid
211
Y
3+
h
c
a
(b)
Fig. 7.1. Models of heterogeneous formation of nuclei at 211 particles [489] (a)and
of solubility of 211 phase into liquid, assisted by homogeneous formation of nuclei
(b) [155, 475]

7.1 Modeling of 123 Phase Solidification from Liquid 303
The theoretical analysis leads us to introduce a criterion connected to
conception of undercooling and to compare the G/R ratio with the relation,
m
L
(C
S
−C
L
)/D
L
[739], where C
S
(C
L
) is the ion concentration of Y
3+
in the
solid (liquid) phase at the interface level; D
L
is the diffusion coefficient of the
ion of Y
3+
and m
L
is the slope of the liquidus curve in the temperature–
composition phase diagram. Depending on the various situations presented in
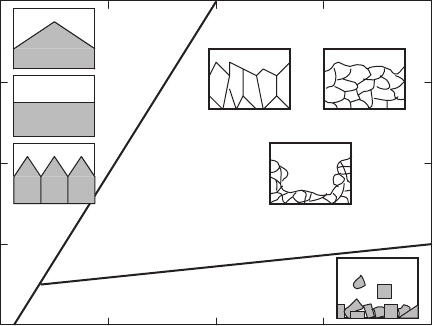
Fig. 7.2 two cases are possible:
(1) If G/R ratio is high, that is, G is high, the slope of the curve giving the
temperature at the interface level is high, whatever the position of this
interface. The comparative behavior of the temperature at the interface
level and the temperature of the liquidus is given in Fig. 7.2c. The equation
G/R ≥ m
L
(C
S
− C
L
)/D
L
(7.1)
Temperature
Distance
T
actual
(c)
T
liquidus
T
∗
(a)
T
∗
Liquid
Solid
Temperature
Distance
C
∗
S
C
∗
L
Temperature
Distance
T
liquidus
Constitutionally
Supercooled
Region
(d)
T
actual
T
∗
(b)
Y-Concentration
Distance
C
∞
Solute Enriched
Layer in Front of
Liquid-Solid
Interface
C
∗
L
Fig. 7.2. (a) Temperature and (b) concentration profiles, showing the constitutional
undercooling; (c) conditions for a plane front; (d) unstable case, where imposed
temperatures are lower than the temperature of the liquidus [286]. T
∗
is the initial
interface temperature
304 7 Modeling of YBCO Oxide Superconductors
is continuously satisfied. The interface temperature evolution is stable in
time, and the solidification front is flat because the interface temperature
follows the temperature of the liquidus.
(2) If the G/R ratio is relatively small, inequality (7.1) is not satisfied, causing
instability of the interface temperature (see Fig. 7.2d), because it should
be continuously re-adjusted to that of the liquidus. Therefore, the solidi-
fication front is not flat, but has cellular (dendritic) shape or consists of
equiaxed blocky (see Fig. 7.3), because the interface temperature fluctu-
ates between the two curves, leading alternatively to a liquid or a solid
phase.
The above results have been used to explain directed solidification of
YBCO after peritectic reaction [890].
The diffusion of yttrium is necessary to re-compose 123 phase in the liq-
uid, that is, for a non-classical peritectic reaction, which is governed by dif-
fusion through melt and additionally demands to attain triple point between
primary, secondary and liquid phases [493]. The driving forces inside the dif-
fusion zone, leading to a migration of yttrium, correspond to concentration
gradients. Two phenomena, presented in Fig. 7.4, have been established for
these concentration gradients [156, 741]: (i) the change of the chemical po-
tential at the “211 phase-liquid” interface caused by the curvature of the 211
particles and (i) constitutional undercooling (ΔT
S
), which corresponds to the
temperature difference between the actual temperature of the solidification
interface and the temperature of the “211 phase-liquid” interface.
The first phenomenon explains a change of 211 particles during melt trans-
formation in 123 crystal. The change of chemical potential, caused by the
7
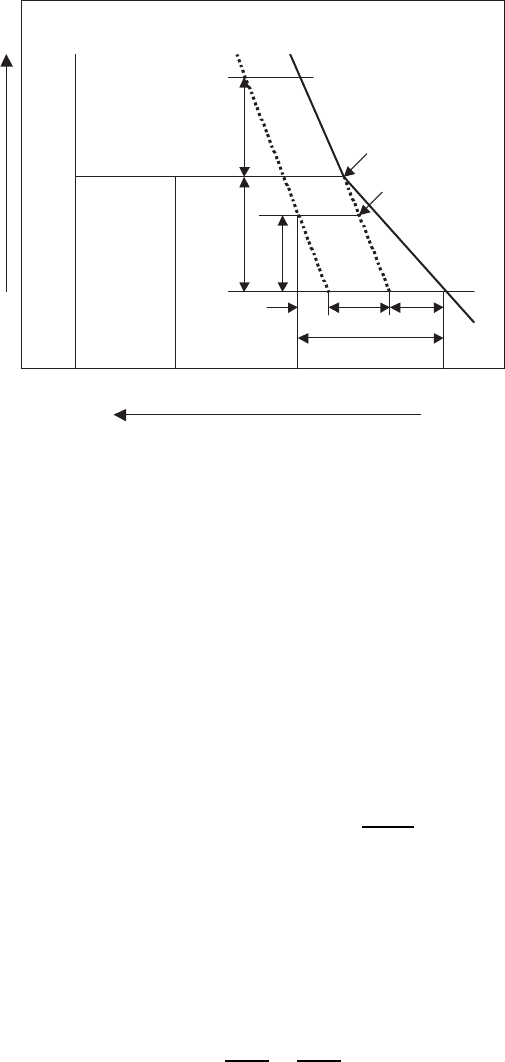
6
5
4
3
46
Growth Rate, R [
µm/s]
Temperature Gradient, lg (G[K/m])
123
123
123 123 123
Faceted
Plane
Front
Cellular
(Dendritic)
Solidification
Equaxed
Blocky
02 8
Fig. 7.3. Effects of temperature gradient and growth rate on the morphology of the
solidification interface [155]
7.1 Modeling of 123 Phase Solidification from Liquid 305
r = rr = ∞
m
L
C
L, r = ∞
≡ C
Lp
m
L
ΔT
r
ΔT
p
T
211
ΔT
G
ΔC
G
ΔC
r
ΔC
S
ΔC
T
123
T
p
Y-Concentration
Temperature
211
123
C
L, 211
0
C
S
211
C
L
123
211
C
L
C
S
123
Fig. 7.4. Schematic phase diagram, showing the undercooling and the concentration
differences as the driving force for the diffusion of yttrium during the peritectic
re-composition of 123 phase [759]
curvature of the 211 particles, relates to the undercooling, ΔT
r
, derived from
the well-known Gibbs–Thomson relationship:
ΔT
r
=2Γ
211
/r , (7.2)
where Γ
211
is Gibbs–Thomson coefficient (= σ/ΔS), σ is the interface energy
between the 211 particle with radius, r, and the liquid, ΔS is the volumetric
entropy of melt. Then, the composition difference of yttrium, ΔC
1
,whichis
considered to be a driving force for diffusion, is expressed using the phase
diagram (see Fig. 7.4), as
ΔC
1
=ΔC
r
= C
211
L(r)
− C
211
L(r=∞)
=
2Γ
211
rm
211
L
, (7.3)
where C
211
L(r)
and C
211
L(r=∞)
are the yttrium concentrations of liquid at the 211
particle and at the 123 interface, respectively; m
211
L
is the liquidus slope of
the 211 phase.
The constitutional undercooling is stated using the second composition
change ΔC
2
, given by extending towards low temperatures the “211 phase-
liquid” liquidus line [476]:
ΔC
2
=ΔC
S
=
1
m
123
L
−
1
m
211
L
ΔT
S
. (7.4)

306 7 Modeling of YBCO Oxide Superconductors
Introduction of a third parameter, ΔC
3
, taking into account the imposed
gradient, completes this model [476]. This term is directly given by the dis-
tance, z, between the solidification interface and the considered 211 particle:
ΔC
3
=ΔC
G
=
Gz
m
123
L
, (7.5)
where m
123
L
is the liquidus slope of the 123 phase. Thus, total difference of the
yttrium concentration, governing the solidification process of the 123 phase is
equal to
ΔC =ΔC
1
+ΔC
2
+ΔC
3
. (7.6)
The next development of the model is connected with the assumption of
the 211 particles to be spheres and consideration of the concentration dif-
ference in yttrium between the 211 phase and the solidification front as the
driving force for the diffusion of yttrium in the liquid phase (see Fig. 7.5) [476].
Assume that the distance between 211 particles is equal to 2δ,andthe
211 phase remains in final structure. The concentration differences of yttrium
near solidification front of 123 phase due to solution of 211 particles are shown
in Fig. 7.5b. Moreover, we assume that the 211 particles are in interfacial
equilibrium with their surrounding liquid and are large enough that the effect
of radius of curvature on melting point is negligible.
1
The phase diagram in
the peritectic region, presented in Fig. 7.4, shows that the temperature of
the growing 123 front is undercooled by an amount ΔT
p
below the peritectic
temperature, T
p
,where
ΔT
p
=ΔT
G
+ΔT
S
+ΔT
C
, (7.7)
where ΔT
G
is the depression of the integrated temperature, resulting from the
temperature gradient, G;ΔT
S
is the maximum constitutional supercooling
ahead of the interface (i.e., temperature difference between the equilibrium
liquidus and the actual temperature at x = δ)andΔT
C
is the temperature
depression, resulting from the deviation in yttrium concentration at the 211
particle interface from that of the peritectic liquid composition, C
Lp
.From
Fig. 7.5b
ΔT
G
= Gδ . (7.8)
The yttrium concentration in equilibrium with the 123 interface (at x =0,
T = T
123
)isC
123
L
, and that at x = δ and T = T
123
+ΔT
G
in equilibrium
with the 211 particles is C
0
L,211
. The dependence of the yttrium distribution
for x>δis given by the equilibrium 211 liquidus. Equating yttrium solvent
rejected from the growing 123 front to that diffusing into the liquid gives
1
If the particles are sufficiently small, this radius of curvature effect could be a
significant, even a major, defining driving force of mass transport, leading to 123
phase solidification [477].
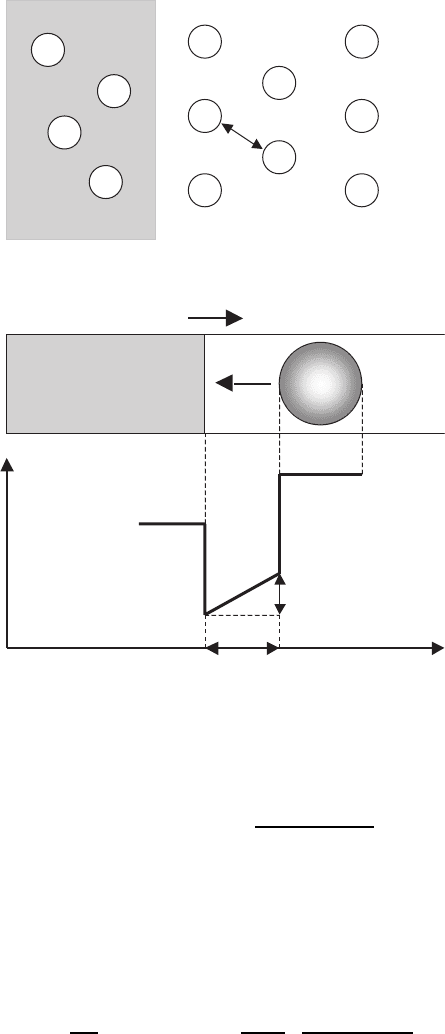
7.1 Modeling of 123 Phase Solidification from Liquid 307
123 Phase Liquid + 211 Phase
(a)
123 211
J
R
Liquid
Distance
Y-Concentration
ΔC
C
S
123
C
S
211
C
L
211
C
L
123
δ
(b)
2δ
Fig. 7.5. (a) Model of peritectic solidification and (b) yttrium concentration profile
near solidification front of 123 phase due to the dissolution of 211 particles. J is the
flux of yttrium ions, which is necessary for growth of the 123 phase
−R(C
123
S
− C
123
L
)=−D
L
C
0
L,211
− C
123
L
δ
, (7.9)
where R is the growth rate of the solidification front. A relation between
interface undercooling (ΔT
p
) and growth rate, R, can be derived, assuming
C
123
S
−C
123
L
≈ C
123
S
−C
Lp
. Moreover, linear liquidus lines, shown in Fig. 7.4,
result in C
123
L
= C
Lp
− ΔT
p
/m
123
L
,andC
0
L,211
= C
Lp
− (ΔT
p
− ΔT
G
)/m
211
L
.
Substitution of these expressions in (7.9) and making use of (7.8) gives
ΔT
p
=
Rδ
D
L
(C
123
S
− C
Lp
) −
Gδ
m
211
L
m
123
L
m
211
L
m
211
L
− m
123
L
. (7.10)

308 7 Modeling of YBCO Oxide Superconductors
Thus, ΔT
p
is linearly proportional to R,whenG is sufficiently small.
Similarly, the next relation can be written between ΔT
S
and R:
ΔT
S
= m
123
L
Rδ
D
L
(C
123
S
− C
Lp
) − Gδ . (7.11)
The quantity ΔT
S
is the constitutional supercooling at x = δ, and it is the
maximum constitutional supercooling in the semisolid region. In solidification
of this type, there must always be finite constitutional supercooling in front
of the growing interface in order to create the compositional driving force for
diffusion from the particle surface to the crystal interface. Assuming an exis-
tence of maximum undercooling [155] and noting that the distance between
the solidification front and considered 211 particle, z = δ,weobtainfrom
(7.11) a relation defining the maximum growth rate, R
max
, compatible with
a plane solidification front:
R
max
=
D
L
z(C
123
S
− C
Lp
)
(ΔT
S
)
max
+ Gz
m
123
L
. (7.12)
Thus, the highest solidification rates compatible with a steady-state growth
are obtained theoretically at the following conditions: (i) with larger under-
cooling, (ii) with higher temperature gradient and (iii) with smaller size of
211 particles after peritectic decomposition (z is directly dependent on the
particle size). Equation (7.12) shows that the maximum solidification rate is
inversely proportional to the distance z between the 211 particles, resulting
from the peritectic decomposition of 123 phase. This suggests a decrease in
the 211 particle size and the addition of very fine 211 powder to the starting
123 precursor, because an increase of the volume ratio of the 211 phase in
the melt for a given particle size results in a reduction of the interparticle
spacing z. In fact, such an addition of 211 to 123 offers multiple advantages:
– It allows the geometric shape of the sample to be kept at high temperature
owing to the formation of a solid skeleton.
– Diffusion of yttrium favors the supply of this species at solidification.
– It compensates the loss of yttrium in the recombination process, where
entrapment of 211 particles takes place.
– Addition of properitectic 211 dispersion refines the grain size of the 211
precipitates, coming from the peritectic decomposition of the 123 phase
(properitectic 211 particles act as nucleation centers).
– It improves the mechanical properties of the textured 123 sample.
– The 211 inclusions, in excess trapped in the textured 123 material, act as
pinning centers, increasing the critical current.
Compare the terms (ΔT
S
)
max
and Gz, taking into account that in a clas-
sical furnace z ≈ 1 μmandG<100 K/cm [190]. Then, it is obvious that
Gz << (ΔT
S
)
max
and the solidification rate appears practically insensitive
to the temperature gradient and is proportional to the undercooling, ΔT
S
.
It should be noted that the case of YBCO system, where the slopes of the

7.1 Modeling of 123 Phase Solidification from Liquid 309
liquidus curves are quite different for 211 and 123 phases, leading to relatively
large driving forces, appears to be favorable for sample texturing.
The directed observations of 123 phase solidification using an IR camera
have found a rate of solidification close to 10
−7
m/s and estimated the diffusion
coefficient of yttrium in the liquid by the value 6 × 10
−11
m
2
/s [310]. From a
practical point of view this solidification rate appears to be quite low. From
(7.12), it is governed by two parameters: ΔT
S
and z. During a slow cooling
rate, r, in a thermal gradient, G, because of the translation, x, of the “liquid-
solid” interface in this gradient the undercooling is given vs time as [190]
ΔT
S
=ΔT
S0
+ rt − Gx . (7.13)
This equation shows that solidification at a constant temperature (r =0)is
possible but is limited by the thermal gradient. In this case, only a large ini-
tial undercooling, ΔT
S0
, can lead to relatively large superconducting crystals
(monodomains).
7.1.3 Models Based on Interface Phenomena
The models [156, 475, 741] considered in the previous section seem in good
agreement with test results, but they do not take into account the interface ki-
netics processes, assuming the crystallization of a pure 123 phase even though
some 211 inclusions are always entrapped in the textured 123 material. More-
over, addition of properitectic 211 dispersion to 123 phase can provoke yttrium
supersaturation at the solidification interface. Then, the diffusion rate of yt-
trium is rapid compared with the propagation of the solidification front, so
the diffusion of yttrium is no longer the limiting factor for the growth of 123
phase. Therefore, it is followed to introduce in consideration interface kinetics
phenomena. The supersaturation can be presented as
σ =
C
I
− C
123
L
C
123
L
, (7.14)
where C
I
is the yttrium concentration at the “123 phase-liquid” interface
and C
123
L
is the yttrium concentration at equilibrium. Three cases can be
distinguished (see Fig. 7.6): (i) the growth rate of 123 phase is governed by
the yttrium diffusion (curve c); (ii) the growth rate of 123 phase is under
mixed control conditions (curve b) and (iii) the growth rate of 123 phase is
governed by the interface reaction (curve a).
A model taking into account the interface phenomena [759] introduces two
rates of solidification (in the ab-plane and in the c-axis direction): R
ab
= k
a
σ
2
and R
c
= k
c
σ,wherek
a
and k
c
are the kinetic coefficients for the a-(or
b-) and c-directions, respectively. The effect of the kinetic coefficient on the
growth rate as a function of the undercooling can be taken into account, us-
ing either square power law dependence or linear one on the supersaturation
[759]. As followed in Fig. 7.7, a linear dependence vs supersaturation leads to
