Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

Modeling of BSCCO Systems and Composites

6.1 Transformation of B i-2212 to Bi-2223 Phase

Understanding the mechanism and kinetics of the Bi-2212-to-Bi-2223 phase

transformation is very important to fabricate Bi-2223 superconductors with

high structure-sensitive properties. The most widely used method of process-

ing Bi-2223 materials is to mix Bi-2212, CaPbO

and CuO powders and to

anneal the mixture in a sealed tube at about 830

◦

C during 10–100 h [119].

All models proposed for phase transformation of Bi-2212 into Bi-2223 suggest

a diﬀusion-controlled, two-dimensional transformation due to diﬀerent mech-

anisms of chemical reactions [33, 352, 358, 635, 650, 726, 1200]. In order to

analyze the kinetics of Bi-2223 formation, the Avrami equation is usually used

[358, 650, 1200]:



1 − C



= K

exp(−U/RT)t

, (6.1)

where C is the fraction of Bi-2223 phase transformed at time t, T is the

temperature, U is the activation energy, K

=1.71 × 10

−22

is the rate con-

stant, R is the universal gas constant and α is the Avrami exponent. The

Avrami exponent α obtained from test data can provide some insight into

the reaction mechanism. Almost all of the above-mentioned authors conclude

that their data support a diﬀusion-controlled, two-dimensional transforma-

tion of Bi-2212 into Bi-2223 phase. The values of the Avrami exponent, which

they obtained, varied greatly, ranging from 0.5 [1200] to 1–1.5 [358, 650].

This, seemed to be more consistent with one-dimensional diﬀusion-controlled

transformation mechanism with a varying nucleation rate [453]. At the same

time, transmission electron microscope (TEM) investigations, using electron

diﬀraction and lattice imaging, show that during the annealing process, the

Bi-2212/ Bi-2223 system consists of fast-growing intercalating Ca/CuO

bi-

layers instead of compact Bi-2223 domains [66]. Unlike the conventional

nucleation-and-growth mechanism, where reactant diﬀuses from grain bound-

aries into the interior of the bulk material, leading to a compact propagating

270 6 Modeling of BSCCO Systems and Composites

“front” of the product, the transformation from Bi-2212 to Bi-2223 phase

appears to be accomplished via the layer-by-layer intercalation of the extra

Ca/CuO

planes into the Bi-2212 matrix. In this case, the Ca/CuO

bi-layer

insertion into the matrix during transformation leads to formation of an edge

dislocation [118]. Hence, it becomes obvious that the fast intercalation of in-

dividual Ca/CuO

plane into the Bi-2212 matrix is more probable as the

path for Bi-2212 to Bi-2223 transformation than nucleation and growth of the

Bi-2223 compact region.

The growth of the intercalant Ca/CuO

planes occurs much faster than

the bulk cation diﬀusion. Then, it may be assumed that a distinct diﬀusion

mechanism acts in the Bi-2212/Bi-2223 system, in which cation diﬀusion takes

place through the cylindrical cavity created by the edge dislocation, which ac-

companies the insertion of a Ca/CuO

plane. These cavities are located at the

interfaces between Bi-2212 and Bi-2223 phases, where the reaction occurs. As

the transformation progresses, these pores move with the Bi-2212/Bi-2223

interface; thus, the reaction progresses uninhibitedly. Based on the above as-

sumption and the layer-rigidity model [117, 1056] modiﬁed to the Bi-2212/

Bi-2223 system, we consider the cation diﬀusion mechanism and calculate the

size of pointed void [118, 119].

6.1.1 Edge Dislocations as Channels for Fast Ion Diﬀusion

The transformation of Bi-2212 phase to Bi-2223 one can be regarded as chem-

ical reaction between the Bi-2212 precursor and the secondary phases such as

CaPbO

and CuO, to provide the required surplus of Ca and Cu. As shown

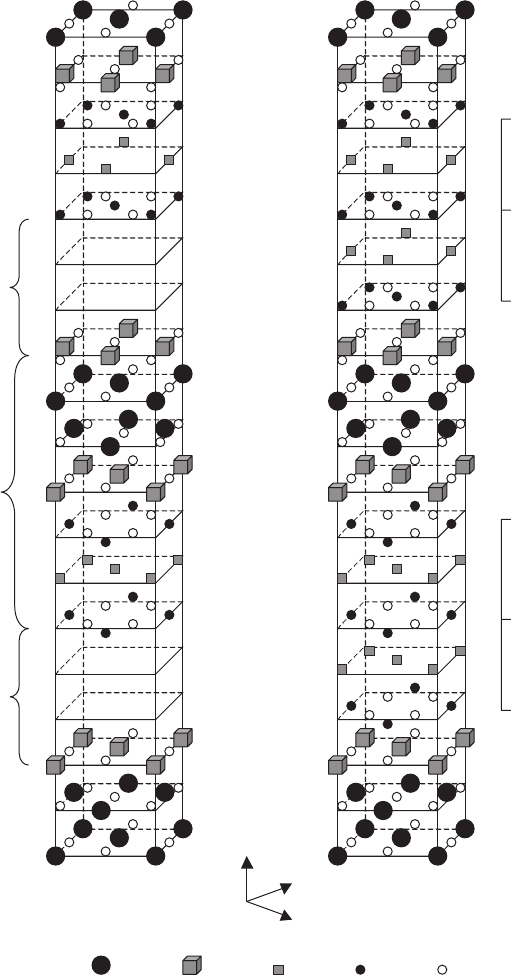
in Fig. 6.1, the only structural diﬀerence between Bi-2212 and Bi-2223 is a

pair of extra Ca/CuO

planes (in the case of Bi-2223) at the corresponding

lattice expansion. Therefore, it is convenient to divide the Bi-2212-layered

structure into two parts, namely (i) the block layers (called “host layers”

below), which consist of BiO, SrO and the Ca/CuO

plane in Bi-2212 and

(ii) the “gallery layers” into which the extra Ca/CuO

planes are inserted in

the case of Bi-2223. Thus, we can consider the Bi-2223 as a stacking fault of

Bi-2212. Therefore, the interfaces in a transforming system between Bi-2212

and Bi-2223 layers can be considered as an edge dislocation. The approxi-

mately cylindrical pore created at the additional half plane of this dislocation

is a line of vacancies, which can be an easy path for the additional Ca, Cu and

oxygen ions to diﬀuse from the surface (or grain boundary) into the bulk mate-

rial, provided the size of the pore is large enough. The size of the pores depends

on the rigidity of the block layer as well as the compressibility of the Ca/CuO

plane along the c-axis. Obviously, the more rigid the layer the larger the pore.

In the limit of inﬁnite layer rigidity, the size of the pore will be inﬁnite.

At the annealing temperature about 830

◦

C, both CaPbO

and CuO are

liquid. The grinding and mixing prior to the annealing make sure that this

liquid phase is evenly coated around each Bi-2212 grain. As the Ca/CuO

plane nucleates near the surface of the Bi-2212 grain (or grain boundary), the

6.1 Transformation of Bi-2212 to Bi-2223 Phase 271

Bi-2212

Gallery

Block

Layer

Gallery

BiO

SrO

CuO

SrO

BiO

SrO

BiO

Bi-2223

CuO

Ca Cu

Fig. 6.1. The unit cells of Bi-2212 and Bi-2223. The layered structure of Bi-2212 can

be divided into block layers and galleries for intercalation of the additional Ca/CuO

plane to form Bi-2223. The “gallery height” in the Bi-2212 structure is shown here

expanded from its normal value for clarity of comparison of the two structures [119]

272 6 Modeling of BSCCO Systems and Composites

pore created by the partially inserted Ca/CuO

plane opens up a channel for

the reactant ions to diﬀuse into the bulk. Thus, it permits the edge dislocation

to climb and the reaction to proceed rapidly at this location. Therefore, it can

be assumed that the transformation from Bi-2212 phase to Bi-2223 is limited

by he nucleation rate of the Ca/CuO

plane near the Bi-2212 grain boundary

and the diﬀusion of reactant ions along the moving dislocation lines.

6.1.2 The Layer-Rigidity Model

The volume expansion at the cores of the edge dislocations (caused by ad-

ditional atomic half-planes) formed during the Bi-2212 to Bi-2223 transfor-

mation is connected with the large anisotropy in physical properties of these

layered systems. It is reasonable to assume that the major expansion takes

place along the direction perpendicular to the layers, denoted as the c-axis. As

it has been shown by diﬀraction tests, the lattice parameters along the a-or

b-axis change very small during Bi-2212/Bi-2223 transformation. At the same

time, the lattice parameter along the c-axis increases from 30.9 to 37.8

A [119].

Basing on the structural diﬀerence between Bi-2212 and Bi-2223 phases,

it is regarded as an insertion of Ca/CuO

in the interior of Bi-2212 matrix.

Then, the Bi-2212/Bi-2223 system can be considered as a type of intercala-

tion compound in the form of A

1−x

L with 0 ≤ x ≤ 1, where B is the

intercalant (additional Ca/CuO

layer in Bi-2223 phase), A is a vacant layer

in the Bi-2212 phase (see Fig. 6.1), which will be considered as an inter-

calant of a smaller size, and L denotes the host layer which represents the rest

of the structure. The single phases Bi-2212 (AL) and Bi-2223 (BL)present

the limiting cases for x =0andx = 1, respectively. The dislocation at the

Bi-2212/ Bi-2223 interface can be modeled as an intercalation compound with

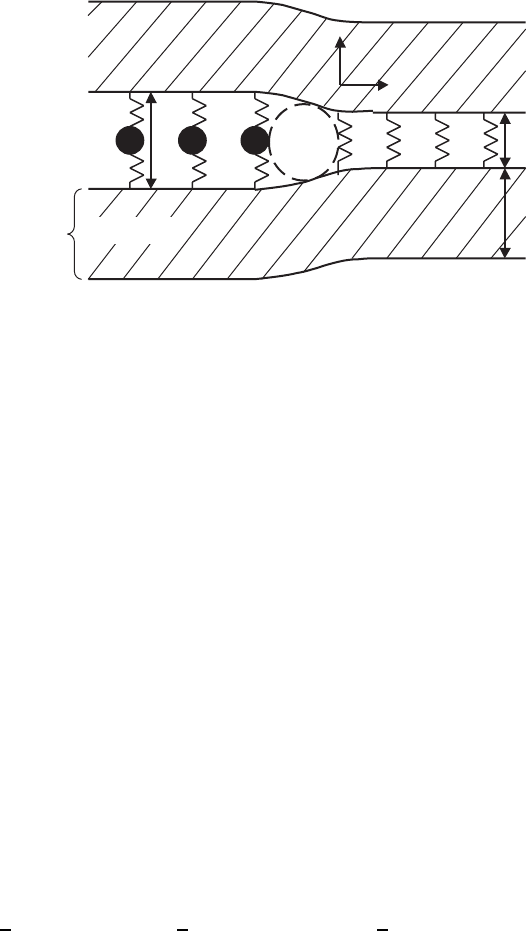
B, occupying the semi-inﬁnite plane, as shown in Fig. 6.2.

Two diﬀerent models have been proposed to study the c-axis expansion

of intercalation compounds [117, 1056]. In both models, it is assumed that

the host layers have ﬁnite transverse as well as bending rigidity. At the same

time, the intercalants have ﬁnite compressibility and diﬀerent sizes. In the

ﬁrst model (bi-layer model) [1056], it is assumed that compressibility of the

host layer is much smaller than that of the intercalant, that is, the correlation

between various galleries can be ignored. In the second model (multiplayer

model) [117], it is assumed that the compressibility of the host layer is much

larger than that of the intercalant, that is, the correlation between various

galleries can be mapped into an Ising-type model. It may be suggested that

the ﬁrst type model is more suitable for Bi-2212/Bi-2223 compound. Let the

compressibility of the host layer be about 10% of that of the intercalant,

because the compressibility of the host layer is inversely proportional to its

thickness, but this thickness is much larger than the mean gallery height in the

Bi-2212/Bi-2223 compound. Here, a spring model that describes both the layer

rigidity and the size and stiﬀness of the intercalant is considered (see Fig. 6.2).

6.1 Transformation of Bi-2212 to Bi-2223 Phase 273

Void

Ca/CuO

Host Layer

Fig. 6.2. Side view of the intercalants in the transforming Bi-2212/Bi-2223 system.

The additional Ca/CuO

plane is shown schematically as large intercalant “atoms.”

The rest of the structural features are shown schematically as the “host layer.” The

separation between the host layers is given by the local gallery height, h

[119]

Consider a layered system with composition A

1−x

L,whereL represents

the host layer of thickness H, which consists of BiO, SrO and Ca/CuO

planes

in the Bi-2212 phase; A and B are two various types of intercalants, which

occupy a set of well-deﬁned lattice sites. The total energy of the system can

be presented by a sum of two major contributions: one associated with the

interaction between the intercalants and the host atoms and the other be-

tween host atoms themselves. It is assumed that the intercalants are “frozen”

into the align structure (i.e., the nucleation time of the Bi-2223 phase is much

shorter than the time for diﬀusion of the Ca, Cu and O ions from the grain

boundary to the bulk). Thus, the direct interaction energy between the inter-

calants does not play any role in layer distortion. Because the compressibility

of the host layer is much smaller than the intercalant, the interlayer correla-

tion is mostly related to the various thickness of the host layer instead of the

correlation between intercalants of various galleries. As the variation of the

host layer thickness, ΔH, is very small compared to H, it can be neglected by

the interlayer correlation and be considered a single gallery, bounded by two

host layers with intercalants, occupying the lattice sites inside the gallery.

Following [119], the total energy of the host layer-intercalant system, pre-

sented in Fig. 6.2, can be written as

E =

− h

)

i,δ

− h

i+δ

)



− h

i+δ

)



(6.2)

where h

is the local gallery height at site i, where an intercalant (either A or

B)sits;h

is the gallery height for the pure system AL or BL(h

=2.21

for Bi-2212 (AL)andh

=6.18

A for Bi-2223 (BL) from the diﬀraction

measurements); K

is the spring constant, representing the compressibility

274 6 Modeling of BSCCO Systems and Composites

of the local intercalant i. The terms, involving the spring constants K

and

, describe, respectively, transverse and bending rigidity of the host layers

[1056]. They are related to the elastic constants of the Bi-2212 compound by

the following relations:

; (6.3)

12a



+ c

− 2c



, (6.4)

where a

=3.8

A is the lattice constant in the ab-plane and H =14.35

Ais

the thickness of the host layer. The required elastic constants for Bi-2212 have

the next values [119]: c

=24.08 ×10

dyn/cm

; c

=6.71 ×10

dyn/cm

;

=14.59 × 10

dyn/cm

; c

=6.18 × 10

dyn/cm

The compressibility K

= K

(A) of the intercalant A (the vacancy) can

be obtained from the elastic constants as

. (6.5)

The compressibility K

= K

(B) of the intercalant B (the Ca/CuO

plane) cannot be calculated due to the lack of data for the elastic properties

of Bi-2223. However, it can be assumed that K

. Then, calculate the

gallery height for the case of K

= K

, estimating thus the minimum size of

the pore. Minimizing E in (6.2) with respect to h

, we ﬁnd

Mh = Φ , (6.6)

where M is a tridiagonal matrix with elements

= K

+2K

+6K

; M

i,i±1

= −K

−4K

; M

i,i±2

= K

, (6.7)

but h and Φ are two column vectors:

h =

⎛

⎜

⎝

...

⎞

⎟

⎠

; Φ =

⎛

⎜

⎝

...

⎞

⎟

⎠

. (6.8)

By diagonalizing matrix M, h

can be obtained. In the case of K

= K, the dispersion relation for the algebraic system is given as [119]

= K +2K

[1 − cos(qa

)] + 4K

[1 − cos(qa

)]

, (6.9)

and the expanded form of (M

−1

)

can be expressed as [119]

−1

)

exp[iqa

(n − m)]

, (6.10)

6.1 Transformation of Bi-2212 to Bi-2223 Phase 275

with q =2πr/Na

; r =1, 2 ...N and λ

being the eigenvalue of the matrix

M.Thenwehave

−1

)

iqa

(n−m)

. (6.11)

Considering a system with half of the yz-plane occupied by intercalant B

(i.e., Bi-2223 phase), we assume the dislocation disposes at y = z =0,and

the equilibrium height h

is deﬁned as

⎧

⎨

⎩

, for n = −

+1, −

+2,...,−1;

, for n =1,...,

− 1,

(6.12)

Taking the limit of N →∞and changing the summation over q by inte-

gration, we ﬁnd that

h(y)=

+ h

− h

4π



K sin [θ (y/a

− 1/2)]

sin(θ/2)

dθ, (6.13)

where θ = qa

and λ

= K +2K

[1−cos(θ)]+ 4K

[1−cos(θ)]

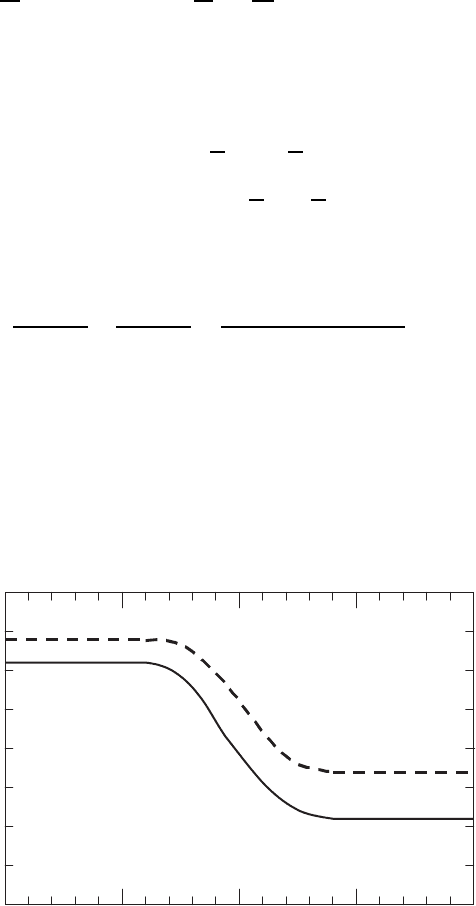
. The solid line

in Fig. 6.3 shows the proﬁle of h

for K

= K

and the values of parameters

deﬁned in (6.3)–(6.5). The obtained results can be compared with the model

of the stacking fault, presenting an additional CuO plane in the YBa

matrix. For this, the theoretical proﬁle of h

is calculated, using the elastic

constants, obtained from the atomistic simulation of YBa

[44], and is

shown by dashed line in Fig. 6.3.

y (A)

(A)

−40 −20

20040

Fig. 6.3. The spatial proﬁle of the gallery h

. Solid line presents Bi-2212/Bi-2223

system, but dashed line corresponds to YBa

/YBa

system (at K

= K)

276 6 Modeling of BSCCO Systems and Composites

Of the three types of reactant ions (Ca

, Cu

and O

2−

), the largest is

2−

, which has a diameter of about 2.9

A. As it is shown in Fig. 6.3, the

lateral size of the pore is about twice as large as the oxygen ion diameter, if

we consider the pore to be the region, where h

≥ 3

Afory ≥ 0. Hence, the

dislocation line is indeed likely to be an easy path for reactant ions to diﬀuse

from the liquid phase at the Bi-2212 grain boundary into the bulk, causing

the edge dislocation (the additional Ca/CuO

plane) to rapidly climb into

Bi-2212.

6.1.3 Dynamics of Bi-2223 Phase Growth

The Avrami exponent in the Bi-2212-to-Bi-2223 transformation using (6.1)

and presented layer-rigidity model is estimated. Because the reactant always

contacts with the Bi-2212/Bi-2223 interface, the reaction rate of Bi-2212 to

Bi-2223 phase perpendicular to the dislocation line is independent of the vol-

ume fraction of Bi-2223 phase, and the growth in this direction is very fast.

Therefore, it is necessary to regard only the diﬀusion along the dislocation

line and assume that the reactants are consumed immediately upon reach-

ing the Bi-2212/Bi-2223 interface, because the diﬀusion is probably a much

slower process than any local rearrangement of atoms, which might be re-

quired. Then, the growth rate of the product layer along the dislocation line

is given as [119]

dl/dt = D/l , (6.14)

where l is the distance from the grain boundary measured along the dislocation

line and D is the eﬀective diﬀusion factor of the reactant ions. Because the

diﬀusion factor and the pore size (see the previous section) are independent

of the volume fraction of Bi-2223, dividing variables and integrating (6.14),

we obtain

l =

√

2Dt . (6.15)

The volume of the reactant ions, consumed by the formation of the product

phase, is given as

R(t)=S

√

2Dt

1/2

, (6.16)

where S is the size of the pore. For a Bi-2212 grain with volume V ,thenumber

of Ca/CuO

planes nucleated at the grain boundary in the time range between



and (t



+dt



)isI(t



)V dt



,whereI(t



) is the nucleation rate per unit area

of the grain boundary. Hence, the total volume of reactant ions, consumed

at time t (assuming nucleation can occur everywhere at the grain boundary,

including the transformed region), is given as

= A



I(t



)R(t − t



)dt



= S

√

2DA



I(t



)(t − t



)

1/2



, (6.17)

where A is the total area of the grain boundary. Note that V

diﬀer from

the actual volume of reactant consumed because it is assumed that nucleation

6.1 Transformation of Bi-2212 to Bi-2223 Phase 277

can take place in the transformed region. All regions are considered, including

those continuing growth irrespective of other regions. In order to correct this

problem, we sign the volume of the transformed region through V

and state

the relation between V

and V

. Consider a small region, of which a fraction

[1 − (V

/V )] remains non-transformed (where V is the total volume of the

grain). During the time range, dt, taking into account the total transformed

volume, dV

, a fraction [1 − (V

/V )] on the average will be in previously

unreacted material and thus contributes to dV

, while the reminder of the

will be in the already transformed region. Then, we obtain



1 −



. (6.18)

Dividing variables and integrating, we have

= −V ln



1 −



. (6.19)

Let [1 − (V

/V )] = 1 − C,whereC is the volume fraction of Bi-2223.

Substituting (6.19) into (6.17), we obtain



1 − C



√

2DA



I(t



)(t − t



)

1/2



. (6.20)

The volume fraction of Bi-2223 depends directly on the nucleation rate

I(t). It is often assumed that the time dependence of the number of nucleation

sites is a classical ﬁrst-order rate process, that is, [119]

dN(t)/dt = −fN(t) , (6.21)

where f is the frequency of an empty gallery in Bi-2212 phase turns into a

nucleation site for Bi-2223 phase and N(t) is the number of such nucleation

sites at time t. Integrating the above equation yields

I(t)=fN(t)=fN

exp(−ft) , (6.22)

where N

is the number of empty galleries in the Bi-2212 grain at t =0.

Substituting (6.22) into (6.20) and integrating yields



1 − C



√

2DN



1/2

exp(−ft)erf(i



ft)



, (6.23)

where erf(z) is the error function with complex variable z,whichcanbeex-

panded as [566]

erf(z)=

√



−ζ

dζ =

√



z −

−

+ ...



. (6.24)

278 6 Modeling of BSCCO Systems and Composites

Now, we can estimate the Avrami exponent α for various values of f.

In the limiting case, when ft is very small, that is, the time to produce a

Bi-2223 nuclei is much longer than the time to grow the Ca/CuO

plane

through the sample, we can expand (5.24) in terms of ft. Taking into account

(6.24) and the expansion [566]

=1+z +

+ ··· , (6.25)

we obtain



1 − C



√

2DN



3/2

−

5/2

+ ···



. (6.26)

Comparing (6.26) with (6.1), we have α ≈ 1.5, which agrees well with the

test results for the preheated sample [358, 650]. Note that the assumption of

this limiting case is valid only if reactants (Ca, Cu and O) are evenly coated

around the Bi-2212 grains and the Bi-2212 grains are small enough. Therefore,

the model is more consistent with tests with small precursor powder, which are

heat-treated before annealing to ensure the even distribution of the reactants.

On the other hand, if ft very large, that is, the time to produce a Bi-2223

nuclei is much shorter than the time to grow the Ca/CuO

planes through the

sample, we can consider that all the empty galleries in Bi-2212 have turned

into nucleation sites for Bi-2223 before the Ca/CuO

planes begin to grow. In

this case, we ﬁnd from (6.23)



1 − C



√

2DN

1/2

. (6.27)

Hence, α ≈ 0.5. This will be the case if there is local shortage of reactant

ions, which will lead to the slow growth of Ca/CuO

plane. Tests in [1200]

apparently fall into this situation. The pointed study has stated an increase

of the Avrami exponent α together with the temperature from 0.5 at 840

◦

to 0.79 at 870

◦

C. The small value of α in [1200] is due to either the large

Bi-2212 grain size as indicated by the high porosity (∼40%) or the uneven

distribution of the reactant ions. When the temperature rises, the growth of

the Ca/CuO

plane accelerates due to the increase of ion diﬀusion constant,

D. In this case, the reactant ions distribute more evenly around the Bi-2212

grain, thanks to the decreased viscosity of the ionic liquid of Ca, Cu and O.

Thus, the Avrami exponent depends directly on the nucleation rate of the

Bi-2223 phase and growth of the additional Ca/CuO

plane in the Bi-2212

matrix changing between 0.5 and 1.5.

6.1.4 Formation Energy of Bi-2223 Phase

As it is shown in experiments, less than 30 min is enough to intercalate one

Ca/CuO

plane into Bi-2212 matrix across a 2 −μm sample [118]. Moreover,