Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

258 5 General Aspects of HTSC Modeling

10 4 12

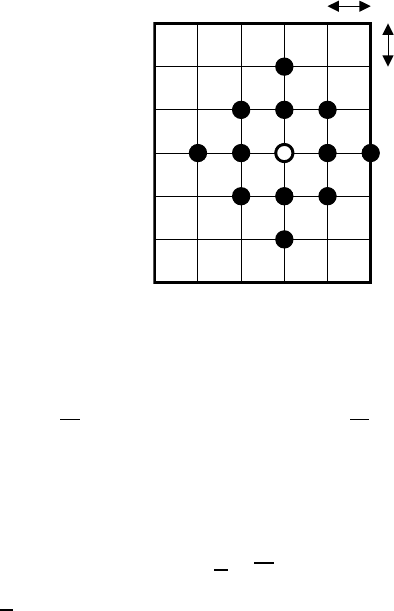
Fig. 5.24. Illustration to the deﬁnition of thermal stresses at point 0

Then, by using the function ϕ, the normal stresses are calculated as

(σ

)

(ϕ

− 2ϕ

+ ϕ

); (σ

)

(ϕ

− 2ϕ

+ ϕ

) . (5.81)

After computation of the thermal stresses, the length of each section at

intergranular boundary is estimated. The mean value of normal stress, acting

on the given section of intergranular boundary, permits to verify the condition

of the boundary microcracking:

√

πl ≥ K

, (5.82)

where

is the mean value of the normal stress on the intergranular boundary

section with length l; K

is the fracture toughness of ceramic. When for the

section, (5.82) is satisﬁed, it is replaced by a microcrack. Obviously, in the

ﬁrst place, microcracks form on the suﬃciently long and stressed boundaries.

The microcracking modeling is repeated cyclically together with solution of

heat conduction problem and calculation of thermal stresses.

A simpler scheme of the microcracking modeling on intergranular bound-

aries may be the next. Based on the test data, a critical grain size during

spontaneous cracking, D

, for considered composition of superconducting ce-

ramic is selected. Assuming, that the grain sizes and facet sizes per grain are

subject to the normal distribution, we obtain [176] D

≈ 2l

,wherel

is the

critical facet size. Taking into account misorientation of grains, a criterion of

microcrack formation at the boundary l is stated [295] as

l/l

≥ 2/[1 + cos(2Θ

− 2Θ

)] , (5.83)

where Θ

(i =1, 2) is the angle between axis of maximum compression in i-

grain and the boundary plane of the grain. These angles are calculated by

using MonteCarlo procedure [176]. Computational algorithm takes into ac-

count that a microcrack grows from triple junctions (i.e., junctions of three

5.5 Study of Statistical Properties of the Model Structures 259

or four grains at square lattice) [295, 572] or is initiated by pore and stops

at the nearest facet node because the facets are usually subject to internal

compressing stresses [295].

5.5 Study of Statistical Properties

of the Model Structures

The computational approach, presented in Sects. 5.3 and 5.4, is the good base

to investigate the size, quantitative, topological parameters and morphologi-

cal features and also to deﬁne structure-sensitive properties of polycrystalline

superconductor. Typical description of ceramic microstructure includes deﬁ-

nition of the size, shape and spatial orientation of the pores and grains. There

are diﬀerent classiﬁcations of materials in the porosity parameters. Another

approach to microstructure description is based on the assumption about its

non-regularity. Either microstructure is estimated by own constant statistical

properties. The void space is correlated with the solid surfaces and forms by

using the grain facets and edges. Architecture of the void space is caused by

the shape, size and mutual disposition of crystallites. The description of solid

matrix characterizes the material space as united whole, including the void

space. Similar approach does not exclude an identiﬁcation of single spatial

structure elements (e.g., pores, grains, etc.) [794].

HTSC microstructure may be described by integral (i.e., global) parame-

ters, deﬁning joint physical properties. An application of integral characteris-

tics permits to abstain from simpliﬁed selection of the grain and pore shapes

and to characterize the material space by using summary values of volume,

surface, curvature, etc., obtained from stereological measurements. Latter es-

timate only global metrics, that is, volume fraction, surface square, length

of linear elements and surface curvature, and also their combined parameters

[513].

The method to deﬁne the volume structure characteristics by using mea-

surements in the observation plane has been named by the statistical recon-

struction [145]. It is based on two statistical principles, namely (i) the structure

sample should have representative volume and (ii) a statistical correlation of

the depicted structure characteristics in the observation plane with actual

structure is necessary. Generally, a calculation of necessary number of the

measurements to obtain unbiased estimation of any stereological characteris-

tic is carried out [145]:

n = (200/y)(σ

/x) , (5.84)

where y is the accuracy level (%); σ

is the average quadratic deviation; x is

the mean value of the stereological characteristic. In the case of given accu-

racy, the number of measurements depends on the variation factor, σ

/x,that

characterizes the uniformity of analyzed structure element. The procedure for

the calculation of necessary measurement number includes the following steps:

260 5 General Aspects of HTSC Modeling

(1) the mean value of the stereological characteristic, x, and variance, σ

,are

estimated for some random sampling;

(2) it is given a necessary accuracy level (y, %) for the mean value of the

measured magnitude;

(3) the number of measurements, n, is calculated from (5.84) which ensures

the necessary accuracy level.

1 20

3 4

(a)

(c)

(b)

(d)

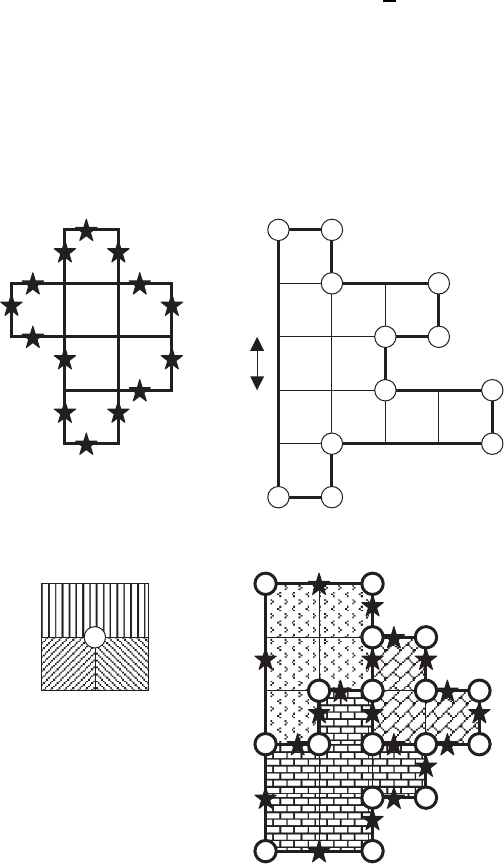
Fig. 5.25. Examples of calculation of some geometrical and topological parameters:

(a) normalized perimeter of grain, L/δ (5.85), n = 7, each from two elements (2, 4)

have two neighbors, element (3) has three neighbors and element (1) has four neigh-

bors: L/δ =3× 7 − (2 × 1+1× 2+1× 3) = 14; (b) number of grain tip (side)

= 12; (c) triple junction (point of intersection of three grain boundaries in square

lattice); (d) Euler’s relation for polyhedron [145]: G − E + V =1,whereG is the

grain number (3), E is the side number (19), V is the top number (17)

5.6 Modeling of Macrocracks 261

Note that (5.84) is obtained by using central limit theorem of statistics,

according to which average values of characteristic, obtained for representa-

tive samplings, are distributed in the normal law relative to the mean value

for corresponding universe. This approach to deﬁne the required number of

measurements is used in the next chapters for study of microstructure and

current-carrying parameters of model superconductors.

A square of single grain or pore is usually estimated by using a detailed

depiction of microstructure. Here, the realized algorithm deﬁnes a disposition

of considered grain and computes the total number of its cells. Then, based

on these squares, the proper grain sizes (or radii) are calculated. The grain or

pore perimeter, L, in 2D case of square lattice may be found (normalized to

the elementary cell size, δ)as

L/δ =

⎧

⎨

⎩

2(n +1) n ≤ 2

3n −

k=2

(k − 1) n>2

, (5.85)

where n is the cell number of considered grain (or pore), k isthepossiblenum-

ber of nearest neighbors for every cell in 2D case and l

is the cell number of

grain (or pore) with k number of neighbors. An example of (5.85) application

is presented in Fig. 5.25a.

5.6 Modeling of Macrocracks

High-temperature superconductors of YBCO or BSCCO are the brittle ma-

terials. Cracks, forming in these materials, as rule, are of I Mode, that is,

fracture (or critical) loading is perpendicular to the crack plane. The cleav-

age planes in HTSC usually correspond to one of the direction of [100] type.

The algorithm for the deﬁnition of arbitrary angles, Θ, formed by the normal

to cleavage plane with direction of tensile stresses, based on the method of

arbitrary twisting of cube, is presented in monograph [808]. This algorithm

models a transgranular cracking of HTSC ceramic, using a critical stress con-

dition. In this case, it is suggested that deﬁnite grain fraction is fractured,

when the stress normal to cleavage plane σ

= σ cos

Θ attains critical value

of σ

∗

(where σ is the tensile stress). At the σ = σ

∗

, the microcrack formation

begins in the grains, where the cleavage planes are perpendicular to the tensile

axis (Θ =0

◦

). The following increase of the stress leads to the crack prop-

agation in the grains, for which 0 <Θ<Θ

∗

,whereΘ

∗

is determined from

the relation σ cos

∗

= σ

∗

. When applied stress attains the value of σ

max

grain cracking into cleavage plane occurs. Then, the angle Θ

∗

max

between the

normal to the cleavage plane and tensile direction is obtained as

∗

max

= arccos(σ

∗

/σ

max

)

1/2

. (5.86)

Experimentally observed crack growth in oxide superconductor can take place

as in grain boundaries (intergranular crack growth), as by cleavage through

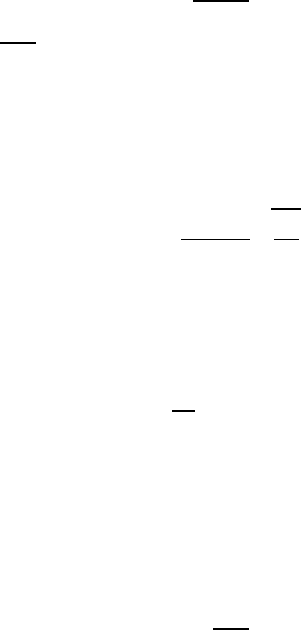
262 5 General Aspects of HTSC Modeling

grain volume (transgranular crack growth). Moreover, there is a mixed charac-

ter of macrocrack propagation, combining above two fracture types. Moreover,

an existence of pores and microcracks into the material structure renders sig-

niﬁcant inﬂuence on crack growth.

Consider a model sample, including layers of rectangular form, N ×M into

units of mean size of the elementary cell, δ. As a ﬁrst mechanism, transgranular

fracture through grain volume is considered. It is known that in the case of

crack growth arbitrarily oriented to tensile direction, the fracture toughness,

, can be found as [144]

cos

, (5.87)

where K

√

Eγ

corresponds to the normal-opening crack, E is Young’s

modulus, γ

is the speciﬁc surface fracture energy and Θ is the arbitrary angle

between the normal to the crack plane and tension direction.

Assume that there is cleavage crack, crossing crystallites in the planes

of {100}-type. Then, the value of K

(j)

for crack path along j-line of the

coordinate lattice with length, h

, is found as

(j)

cos

, (5.88)

where d

is the length of i-grain in the j-line and Θ

is the corresponding

arbitrary angle formed by normal to cleavage plane and tension direction.

Mean fracture toughness of the considered region may be estimated as

j=1

(j)

, (5.89)

where N

is the number of lines in the selected rectangular region without the

lines, including only elements of open porosity.

Then, consider a macrocrack growth along intergranular boundary with-

out microcracks (Fig. 5.26a) and in the existence of microcracks (Fig. 5.26b)

onto the part of the intergranular boundaries. The material fracture tough-

ness, K

, as function of the speciﬁc surface fracture energy, γ

, and Young’s

modulus, E, has the form:



Eγ

. (5.90)

In the case of the rectilinear intergranular boundary, γ

= γ

,whereγ

the speciﬁc grain boundary energy. In the actual sample, either crack trajec-

tory is the arbitrary broken line. The value of γ

can be found through the

ratio of the crack path length, L, to the sample width, h,as

= Lγ

/h . (5.91)

5.6 Modeling of Macrocracks 263

(a)

(b)

(c)

Fig. 5.26. Examples of macrocrack growth, shown by gray line, along intergranular

boundaries in the case of (a) microcracking absence, (b) microcracking presence onto

part of intergranular boundaries and (c) mixed mechanism of macrocrack growth

264 5 General Aspects of HTSC Modeling

In order to compute L, we use a presentation about crack path as on the

graph branch, joining the points at the opposite sides of the model layer. In

this case, the graph branches are constructed, taking into account the inter-

granular boundary lattice. The beginning of the graph tree coincides with

the intersection point of one from intergranular boundaries with the left side

of the sample (see Fig. 5.26). This selection of the crack growth beginning

corresponds to test data, showing that usually a fracture starts from sample

surface. It is clear that a set of the graph tree branches may be selected,

connecting a given point at one side of the layer with arbitrary point at the

opposite side. From the energy minimum condition, a minimum trajectory

corresponds to actual crack path. In order to deﬁne this minimum path, the

Bellman-Kalaba’s algorithm is used [562]. In this case, a problem of minimiza-

tion of the numerical (n + 1)-order graph with tips, x

, is reduced to solution

of the next equation set:



=min(V

+ C

),i=0, 1 ...,n− 1; j =0, 1 ...,n; i = j

, (5.92)

where V

is the length of optimum path between points of x

and x

; C

≥ 0

is the value corresponding to the graph arc (x

). The Bellman-Kalaba’s

algorithm suggests an iteration method for the solution of the minimization

problem (5.92). Supposing V

(0)

= C

; i =0, 1 ...,n−1; V

(0)

= 0, successively

compute

(1)

=min(V

(0)

+ C

); i =0, 1 ...,n− 1; j =0, 1 ...,n; i = j

.........................................................................................

(k)

=min(V

(k−1)

+ C

); i =0, 1 ...,n− 1; j =0, 1 ...,n; i = j

.........................................................................................

(k)

= 0 (5.93)

up to carrying out of the equalities, V

(k)

= V

(k−1)

; i =0, 1 ...,n−1. In this

case, the values of V

(k)

are the minimum values, which deﬁne an optimum

branch of the graph tree. (n−1) iterations are suﬃcient for its determination.

In the considered case, the graph tips coincide with the lattice nodes dis-

posed in intergranular boundaries. In order to accelerate a sorting out of pos-

sible graph branches, Viterbi’s algorithm is used [72]. Only the graph branches

with length, which is not longer than a given inter-nodal distance, l

(or length

of the crack unit jump), are considered. If these paths are to be more than one,

a priority is given to the path with the ﬁnal tip disposed from the initial one

at maximum distance along the coordinate perpendicular to tensile direction.

The ﬁnal graph tip, found in this way, corresponds to the crack tip after its

jump; at the same time, this tip is assumed to be initial for the next graph tree,

and so on. In order to optimize the selection process, it is expedient to limit a

5.6 Modeling of Macrocracks 265

number of considered graph tips in accordance with the length of the macroc-

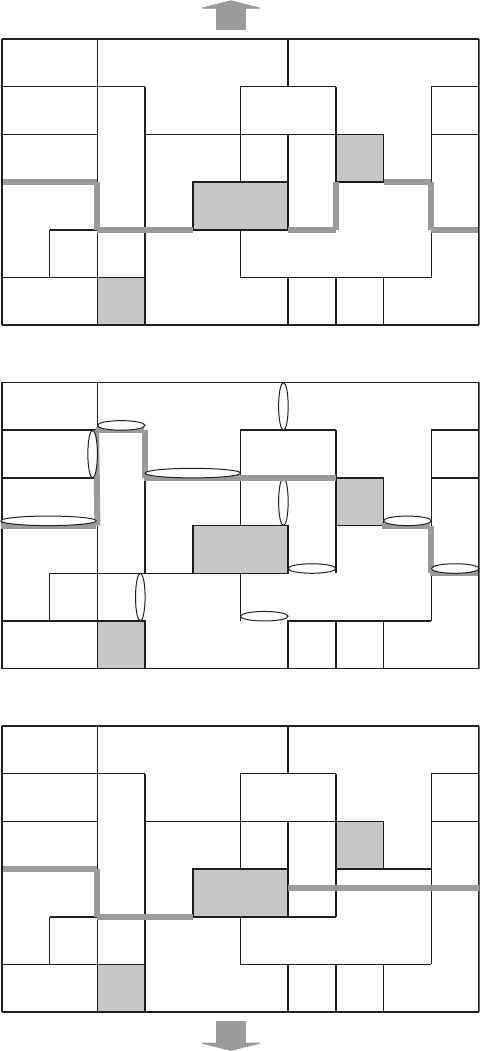
rack unit jump. The region of possible crack unit jumps is shown in Fig. 5.27a.

In order to deﬁne a crack path, taking into account ceramic porosity, it is

natural to assume that in the case of the crack hit in a pore, the crack tip

blunts, causing a diminution of stress concentration. In our model, the pointed

drag is depicted by adding the pore boundary length, crossed by the crack,

to the crack length. The normalized boundary length of the pore, L

/δ,is

calculated in 2D case using (5.85).

Now, the values of C

used in (5.93) for calculation of the crack path can

be found:

⎧

⎪

⎨

⎪

⎩

0 i = j

/δ i, jare two nearest nodes at the grain boundary

/δ i, jbelong to grain boundary of the same pore

∞ in other cases

(5.94)

where C

= C

and L

=2δ is the double length of elementary cell side.

Solution of (5.92)–(5.94) deﬁnes the whole crack trajectory. The calculation

of fracture toughness for the model sample is carried out as

i=1

(i)

, (5.95)

where K

(i)



Eγ

(i)

; γ

(i)

=(L

)γ

and N is the number of considered

crack paths by which an averaging of the fracture toughness is carried out.

Then, consider a model sample of superconducting ceramic, taking into

account microcracks, substituting a part of intergranular boundaries. As it

has been demonstrated, these microdefects can nucleate, in particular due

to residual thermal stresses, caused by the thermal expansion anisotropy of

grains and/or by the deformation mismatch of phases.

It is natural to assume that a microcrack, crossing the macrocrack path,

renders a drag eﬀect if the macrocrack crosses the microcrack at a junction

of two sections of the microcrack (it is not important, with same direction or

disposed at angle). In other cases (i.e., at the macrocrack hit in one of the

microcrack tips), an acceleration of the macrocrack growth occurred. In the

ﬁrst case, the length of the microcrack surfaces is added to the macrocrack

length. At the same time, in the second case, it is suggested that the macroc-

rack propagates on the whole microcrack length. Hence, relation (5.94) should

be modiﬁed as in the following equation:

⎧

⎪

⎨

⎪

⎩

0 i = j or at favorable disposition of microcrack

/δ i, j are two nearest nodes at intergranular boundary

/δ i, j belong to the boundary of the same pore

/δ at unfavorable disposition of microcrack

∞ in other case

(5.96)

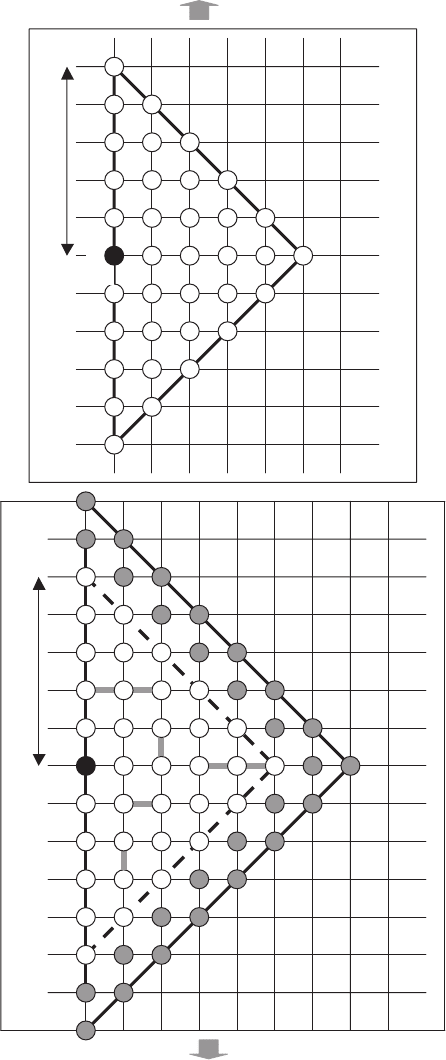
266 5 General Aspects of HTSC Modeling

(a)

(b)

Fig. 5.27. Possible region of macrocrack unit jump during intergranular fracture

(where l

is the length of the crack unit jump): (a) boundary microcracking is absent;

(b) part of intergranular boundaries is replaced by microcracks (gray); circles show

considered nodes; additional nodes, caused by the intergranular nicrocracking, are

shown by gray color

5.6 Modeling of Macrocracks 267

In this case, C

= C

and L

/δ is the normalized length of the microc-

rack boundary. The microcrack existence leads to a change of the crack unit

jump compared to the case of absence of the grain boundary microcracking

(see Fig. 5.27b). When there are points for favorable growth of the crack,

initially considered region (Fig. 5.27a) should be expanded. The number of

additional layers is found by the maximum summary number of rectilinear

sections of microcracks disposed in one line (or column) of the initial region

(see Fig. 5.27b).

Third mechanism of crack growth is mixed. It implies a possibility of tran-

sition from one fracture mechanism to the other at deﬁnite conditions (see

Fig. 5.26c). Here, at either stage, three possible variants of crack growth are

considered (either two intergranular and one transgranular cracks or two trans-

granular and one intergranular cracks) depending on character of the crack

growth at the previous stage. For either from the three competing cracks, the

value of K

is calculated by using (5.88), (5.89) and (5.95). Then, a minimum

value of K

states a path of the crack growth at considered stage. Again, a

ﬁnal crack tip becomes an initial one at the next stage of the crack growth.

The process is continued up to attainment by the crack of opposite side of

the sample or open porosity. The consideration of mixed mechanism is caused

by the replacement of the crack growth character at diﬀerent sections that is

supported by existing test results for diﬀerent ceramics [849]. A fabrication of

optimum HTSC microstructures implies an inclusion in the consideration of

proper crack shielding (ampliﬁcation) mechanisms and the material fracture

resistance. These mechanisms for YBCO and BSCCO ceramics and compos-

ites will be considered in Chaps. 8 and 9.