Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

320 7 Modeling of YBCO Oxide Superconductors

123

211

Liquid

123

Liquid

123 C

211

123

211

123

Liquid

211

123

Liquid

(a)

(b)

(c)

(d)

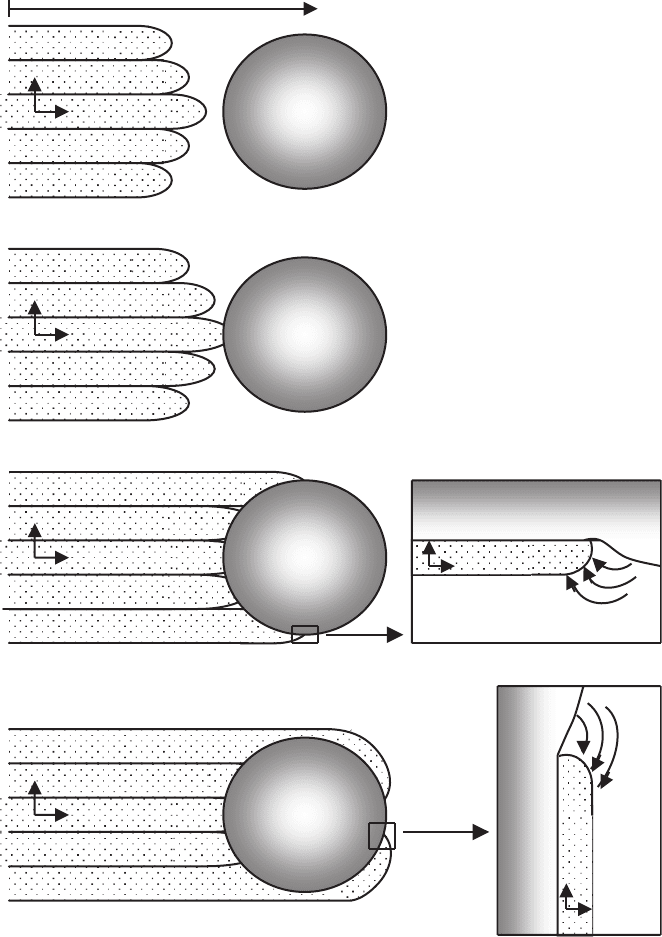
Fig. 7.16. Competing growth of 123 platelets near a 211 particle, leading to quasi-

single crystalline material via a zipper-like mechanism. (a) The platelet closest to

the 211 particle forms a bridge, (b)thec-axis growth of platelet A is in competition

with the fast ab-plane growth of the adjacent platelet B,(c, d) explain enlarged

platelet thickness of the outer platelets after passing the particle [936]

7.1 Modeling of 123 Phase Solidiﬁcation from Liquid 321

(a)

(b)

20 μm

123

211

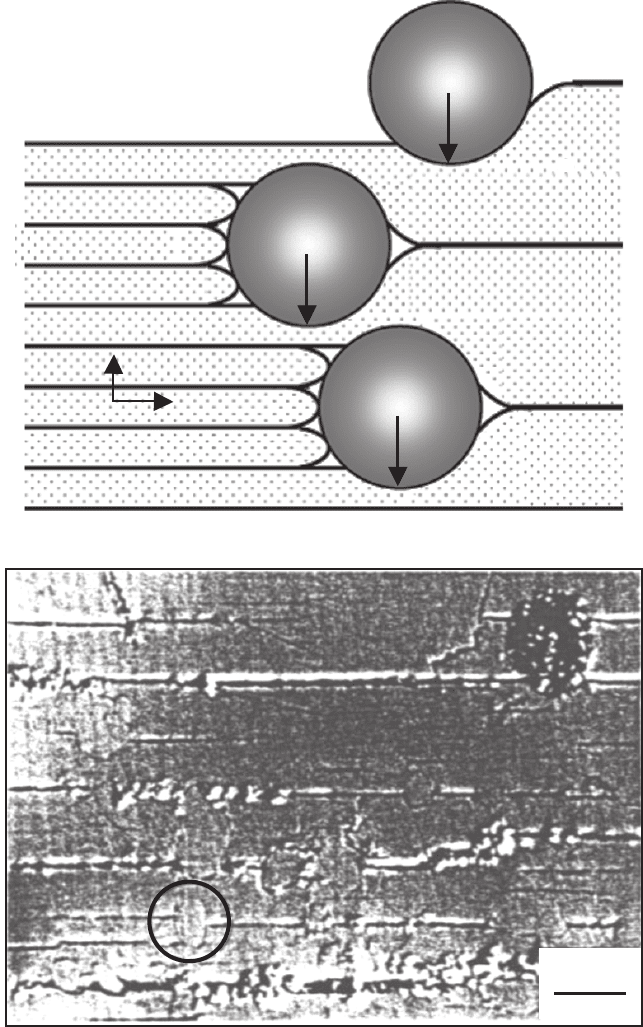
Fig. 7.17. (a) A zipper mechanism and (b) experimental evidence for this mecha-

nism [936]

322 7 Modeling of YBCO Oxide Superconductors

211

123

(a)

123

211

123

(b)

(c)

123

Fig. 7.18. 123 pseudo-grains (platelets), passing a 211 particle of approximately

the same dimensions. Predominant growth, when passing the particle is in the paper

plane in the case (a) and in a plane perpendicular to the paper plane, but parallel

to the ab-planes, in the cases (b)and(c) [936]

7.1 Modeling of 123 Phase Solidiﬁcation from Liquid 323

211

123

Liquid

211

Liquid

123

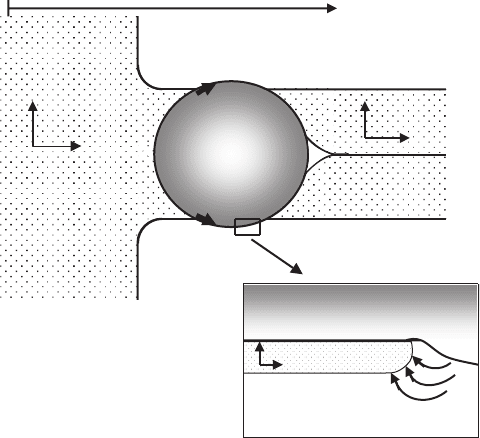
Fig. 7.19. Change in the growth morphology of a planar 123 interface, evoked by

a 211 particle [936]

7.1.5 Modeling of Solidiﬁcation Kinetics

Only thermodynamic and chemical representations cannot totally describe

growth processes in the Y(RE)BCO compounds. It is also necessary to in-

clude in consideration a kinetic process of the 123 phase solidiﬁcation. As is

followed from tests [1104], during the growth processes, the residual phases are

pushed and distributed along the growing steps and sometimes are trapped

in the 123 matrix, leading to the formation of microcracks. Their shape

correlates with the rapid lateral growth that occurs in the ab-plane. This

can lead to the formation of multi-grain domains as schematically drawn in

Fig. 7.20.

Computer simulation of 2D growth kinetics of 123 front near 211 particles

in the ac-andab-plane is carried out in [1104] on the basis of Eden kinetics

model (see Appendix D) for stochastic cell-by-cell growth of compact clusters.

On a square lattice, we take a box of size L with periodic boundary condi-

tions in the abscissa direction. The growing crystal is represented by the set

of occupied sites on the lattice (see Fig. 7.21). At each step of the growth, the

set of empty sites in contact with the growing surface deﬁnes the perimeter of

the solidiﬁcation front (the circles show these sites). A site of the perimeter

is randomly occupied, following the probability rule described below. This

deﬁnes a new perimeter conﬁguration, and the same process is repeated.

324 7 Modeling of YBCO Oxide Superconductors

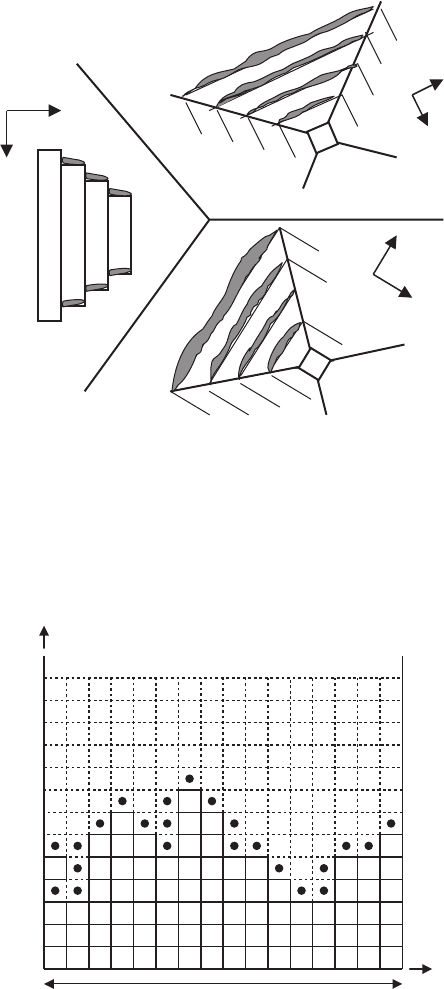
Fig. 7.20. A pyramid-like picture, sketching the formation of a polycrystalline

region in the solidiﬁcation process. Crystallographic orientations are emphasized

and residual phase (gray regions) along growing steps [1104]

L = 16

Fig. 7.21. Crystal front simulated using the isotropic Eden model. The black circles

illustrate the perimeter sites

7.1 Modeling of 123 Phase Solidiﬁcation from Liquid 325

In such a model, an occupied site can represent a unit cell or a cluster of

123 cells.

It is known that an anisotropic growth rule simulates precipitation pro-

cesses [689], as well as the growth of cell colonies [52]. In order to simulate an

anisotropic growth front in the ab-andac-planes, we consider two variants of

the Eden model [1104]:

(1) Model I simulates the solidiﬁcation front in the ac-orbc-plane, considering

a square lattice oriented in [100] and [001] directions. At each step of the

growth, a growing probability, P , is calculated on each perimeter site, and is

given by

P ∼ exp(p

+ p

) , (7.21)

where N

and N

are the number of occupied nearest neighbors (nn) in the a

and c directions, respectively; p

and p

are the anisotropic growth parameters.

Then, the set of these probabilities (deﬁned on the perimeter) is renormalized

in the interval [0, 1]. A random number generator chooses the growing site

as in a Monte-Carlo simulation. This site is then occupied, deﬁning a new

perimeter with the next repetition of the whole process.

Note that the exponential law simulates a curvature eﬀect (or a so-called

Gibbs–Thomson eﬀect) [1146]. When p

, the growth probabilities are

more important in empty sites linked to the crystal, following the a-axis di-

rection. It results in a faster growth in the [100] direction than in the [001] di-

rection, simulating an anisotropic solidiﬁcation process in the ac-plane. When

= p

= 0, the growth process reduces to a simple Eden’s model. When

, the growth is trivial: the front remains ﬂat and parallel to the sub-

strate (i.e., to the [001] direction).

(2) Model II simulates the solidiﬁcation front in the ab-plane. In order to

simulate the [110] as the fast growth direction, the growth probability, P ,

calculated on each site of a square lattice is given by

P ∼ exp(p

+ p

dnn

) , (7.22)

where N

and N

dnn

are the number of occupied nearest neighbor sites (nn)

in the [100] or [010] directions and diagonal nearest neighbor sites (dnn) in

the [110] directions, respectively; p

and p

dnn

are the growth parameters.

The interaction with the diagonal nearest neighbors (dnn) is introduced in

this model in order to take into account the diagonal fast growth directions

in the ab-planes. When p

= p

dnn

= 0, the model also reduces to the simple

Eden’s model.

In both models, the presence of 211 particles can be simulated, avoiding the

growth process to be achieved in circle-like regions of the square lattice. Thus,

the 211 particles play a passive role, in contrast to, for example, the models

[156, 475, 741], in which these particles provide with yttrium solidiﬁcation

front of 123 phase.

The numerical results [1104], obtained on the basis of above models, es-

timate anisotropic eﬀects of grain growth in the ab-plane (g

110

100

∼ 10)

326 7 Modeling of YBCO Oxide Superconductors

and in the ac-plane (g

100

001

∼ 50), where g

hkl

is the growth probability in

the crystallographic hkl directions. Replacing particles by spins [35], a mag-

netic ﬁeld eﬀect can be simulated and the magnetical texture growth processes

could be further analyzed [184].

7.1.6 Multi-phase Field Method

In order to minimize the processing time as well as improve texture of YBCO

melt-processed bulks, total information about solidiﬁcation isotherm distri-

bution in time and in space is necessary. This also deﬁnes qualitative estima-

tions of a grain growth. The consideration of two-level scaling (in this case the

macroscopic study of thermal ﬁelds and microscopic grain growth processes)

decreases calculation time signiﬁcantly. The macroscopic simulation of ther-

mal ﬁelds in the YBCO samples, sintered into a Bridgman furnace in existence

of the thermal insulation layer between the furnace and sample, has been car-

ried out in [956]. In order to simulate YBCO microstructure formation, three

diﬀerent approaches could be used, namely (i) Monte-Carlo technique [800,

819, 822]; (ii) cellular automata models [302]; and (iii) phase ﬁeld method

[113, 1142]. In this section, we consider in more detail the latter method. The

phase ﬁeld conception has been applied to multi-phase system [1016], and also

to the microscopic simulation of the 123 platelets growth at the existence of

the 211 particles [956].

In the multi-phase ﬁeld model, describing evolution of interphase bound-

ary, each phase is identiﬁed with individual phase ﬁeld, and phase transfor-

mations between any neighbor pairs are considered depending on their own

characteristics. The phase ﬁeld method [142, 1142], based on the Ginzburg-

Landau theory of phase transformations [452, 617, 737, 935, 986], was ap-

plied to the study of structural phase transformations of the “solid-solid”

type in [141]. The theoretical basis was the functional of the local density of

free energy, depending on an order parameter of the system and its partial

derivatives on the spatial coordinates. The order parameter can be a scalar

function, for example, concentration of solid component in the investigation

of the phase transformations of the “solid-liquid” type, which changes from 0

(in liquid) to 1 (in solid). [1016] was limited by the parameters, p

, describing

only local phase state of the system. In this case, each phase ﬁeld is identiﬁed

either with melt or single 123 grain or 211 particle. Their time evolution is

described by the system of non-linear parabolic partial diﬀerential equations

[1016]:

˙p

k(k=i)



∇

− p

∇

) −

− p

− 2m

(ΔT

)]

(7.23)

7.1 Modeling of 123 Phase Solidiﬁcation from Liquid 327

where the point, as usual, denotes the time derivative; the parameters τ

,ε

and m

can be deﬁned through the test values (μ

is the mobility, σ

the surface energy and λ

is the interface thickness) as [1142]

; (7.24)

= λ

; (7.25)

72σ

; (7.26)

− T )

. (7.27)

They calculate through a set of parameters, describing the phase transfor-

mation (i → k), namely (i) the equilibrium temperature of the phase transi-

tion, T

(e.g., the melting temperature, T

, in solidiﬁcation processes); (ii)

the heat release during phase transition, L

(e.g., the melting heat in solidi-

ﬁcation problems); (iii) the driving force of the phase transition, m

, deﬁned

by deviation from equilibrium; and (iv) the diﬀerence, ΔT

, between the

temperature of local cooling of the phase interface and the temperature, cor-

responding to a condition for the local equilibrium of i and k phases. These

equations are coupled with a diﬀusion equation, determining the local con-

centration of yttrium at any position and time. It may by shown that in

simulation of the superconducting structure solidiﬁcation, the solution of con-

stitutive equation for i phase is required to ﬁnd only near interface boundary

with neighbor phase. This set of diﬀerential equations is solved by a ﬁnite

diﬀerence technique, using rectangular lattice [1016].

Evolution of single phase, growing by isotropic way (e.g., liquid droplets in

gas media), leads during interaction of its structure elements to the formation

of 120

◦

-angles in triple points. In the case of multi-phase systems, the triple

junctions between diﬀerent phases can be triple points of the “solid-liquid-gas”

type. Then, considerable diﬀerence between surface energies for the systems

“melt-solid”, “solid-gas” and “gas-melt” leads to formation of triple points

with angles diﬀerent from 120

◦

Diﬀerent crystallographic directions cause anisotropic behavior on ac-

count of crystallographic structure. The investigation of phase transition from

isotropic melt to anisotropic solid leads to corresponding change of equations

for phase ﬁelds. This is attained by either introduction of kinetic factor or

diﬀusion coeﬃcient for phase ﬁeld depending on the orientation of phase

boundary to the crystallographic directions of neighbor grains or phases.

The multi-phase conception may also be used to consider diﬀerent grains

with various spatial orientations, belonging to the same phase. With this

aim in [1016], all orientations are divided into 10 orientation classes (the

Pott’s model), and each class is identiﬁed with own order parameter. Two-

and three-dimensional computed simulation of grain growth with diﬀerent

328 7 Modeling of YBCO Oxide Superconductors

crystallographic orientations has shown a dominant grain growth along the

direction of the solidiﬁcation front propagation.

The couple consideration of the phase ﬁeld equations for thermal and sol-

ubility ﬁelds allows the process of microstructure formation to be modeled

in actual peritectic systems (e.g., YBCO) [604]. The computer simulation re-

sults show coupling of the peritectic phase growth with a solubility of the

properitectic phase. Obviously, the properitectic particles dissolve in liquid

phase, according to their diameters (or surface curvature), increasing local

concentration of yttrium in surrounding melt. As has been shown above, a

microstructure of forming superconductor does not have not ﬂat front, but

creates bridges between solidiﬁcation front and properitectic particles [936].

When the 211 particles are suﬃciently great, the time for their total disso-

lution before interaction with 123 front is insuﬃcient. As a result, they are

trapped by the 123 matrix and can serve as pinning centers (see Fig. 7.22)

[956]. Based on the phase ﬁeld conception [1016], the computer simulation of

a single particle in a population of 211 particles ahead of a growing 123 front

reveals a “virtual pushing” of the particle, displaying in its initial coarsening

before gradual and ﬁnal dissolution (see Fig. 7.23) [938]. The computer results

show that a dissolution/re-precipitation mechanism at least contributes to the

displacement of the 211 particles ahead of a growing 123 front.

Another example of computer simulation [937, 956] relates to the geo-

metrically caused grain growth. In this case, the grain selection is found by

the conditions of their anisotropic growth. This example may be useful for

processing optimization of superconducting tapes. Moreover, the eﬀects of

nuclei grains sizes can be investigated in this way. Computer simulation of

211 particles, deﬁning superconducting properties of YBCO and forming X-

like precipitation, has been carried out in [937]. This yttrium enrichment of

the 123 grain diagonals leads to conclusion observed in experiment that the

2 µ m

Fig. 7.22. The microscopic simulation results, deﬁning engulfment of 211 particles

and bridge formation [956]

7.1 Modeling of 123 Phase Solidiﬁcation from Liquid 329

(a) (e)

(b)

(c)

(f)

(g)

(d) (h)

Fig. 7.23. 211 particle ahead of a peritectic solidiﬁcation front (the front grows from

right to left). The motion of the particle is shown relative to the grid in combination

with initial coarsening and then ﬁnal dissolution [938]