Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

330 7 Modeling of YBCO Oxide Superconductors

precipitation of 211 particles is controlled by the 123 phase evolution. Because

yttrium concentration is greater at the edges and in the angles of growing 123

crystallite, the driving force of the 211 phase dissolution will be smaller in

these sites. Then, the dispersed 211 particles dissolve more slowly and hence

are easily trapped along diagonal directions. The neglected small eﬀects of

volume diﬀusion in solid state and corresponding minimum peritectic trans-

formation cause a stability of these particles in the ﬁnal microstructure [937].

The simulation supports the possibility of eﬀective variation by parameters

especially in relation to geometric composition of superconductor. The ge-

ometrically caused grain growth does not increase the solidiﬁcation rate of

single 123 grains, but optimizes the processing rate of conductor in whole,

considering directed solidiﬁcation of great number of grains simultaneously

with grain nucleation in some sites. The selection of 123 grains for this pro-

cess occurs, using anisotropic growth conditions. Of particle interest is the

grain selection distance, required for the well-oriented grains to overgrow the

misaligned ones (see Fig. 7.24) [956]. In this case, the growth of grains, having

maximum rates and crystallographic orientations parallel to the main direc-

tion of the solidiﬁcation front propagation, accelerates. In contrast, the growth

of grains, perpendicular to the solidiﬁcation front, slows down. That selection

can be used in order to increase processing rate and critical current density in

the melt-processed YBCO. Thermodynamic parameters, used in calculations,

are presented in Table 7.1 [937]. These parameters are either well-known data

for YBCO family or estimations obtained for related materials.

10 μ m

Fig. 7.24. Eﬀect of grain selection investigated by computer simulation method

and using phase ﬁeld approach. Diﬀerent 123 grains are visualized by diﬀerent gray

levels [956]

7.2 Stress–Strain State of HTSC in Applied Magnetic Fields 331

Table 7.1. Thermodynamic parameters used in modeling

Parameter Value

Latent heat 1000 J/cm

Diﬀusion coeﬃcient 10

−6

Peritectic temperature 1288 K

Cooling temperature 37 K

Yttrium concentration in melt

near 211 particle

0.26 mol%

Yttrium concentration in melt

near 123 interface

0.14 mol%

Surface energy 10

−6

J/cm

Linear kinetic factor 0.186 cm/s K

123 interface thickness 1.018 × 10

−4

Thus, the phase ﬁeld method allows some thermodynamic phases in global

non-equilibrium, taking into account local couple interactions of neighbor

phases near the point of thermodynamic equilibrium, to be considered. The

superposition of these couple interactions causes characteristics of triple point

(i.e., multi-phase equilibrium). Then, the solution of equation for multi-

phase ﬁeld deﬁnes the phase transition kinetics, which co-relates with limited

diﬀusion during dissolution or with surface energy of interfaces. The equilib-

rium conditions for phase interface can be selected from existing thermody-

namic databases. Numerous phase diagrams for metallic alloys and ceramics

deﬁne broad potential applications of this method for prediction of HTSC

microstructure evolution.

7.2 Stress–Strain State of HTSC in Applied

Magnetic Fields

HTSC can trap great magnetic ﬁelds (more 10 T) at suﬃciently high shield-

ing currents. In this case, there are signiﬁcant stresses and strains, induced

by the Lorentz force between the shielding current and the magnetic ﬁeld,

which is capable of forming and propagating cracks. One-dimensional stress

distributions in the totally magnetized superconductor have been considered

[492, 879]. Two-dimensional (i.e., axi-symmetric 3D) problem using numerical

methods has been investigated in [1039, 1083].

Here, we consider 2D problem for axisymmetric cylinder, presented in

Fig. 7.25. In the cylindrical coordinate system, the following equations are

obtained for radial and axial displacements, u and ν from the force balance

condition for an inﬁnite-small element [1084, 1085]:

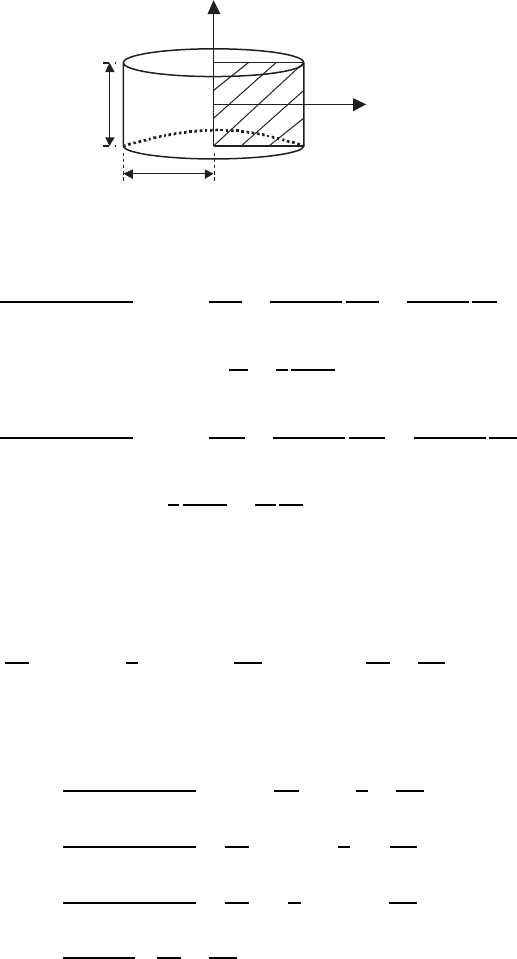
332 7 Modeling of YBCO Oxide Superconductors

Fig. 7.25. Axisymmetric superconducting cylinder considered in this analysis

−E

(1 + ν)(1 − 2ν)



(1 − ν)

∂

∂r

(1 − 2ν)

∂

∂z

(1 − ν)

∂u

∂r

−(1 − ν)

∂

∂r∂z



; (7.28)

−E

(1 + ν)(1 − 2ν)



(1 − ν)

∂

∂z

(1 − 2ν)

∂

∂r

(1 − 2ν)

∂w

∂r

∂

∂r∂z

∂u

∂z



, (7.29)

where F

and F

are radial and axial Lorentz forces, ν and E are Poisson’s

ratio and Young’s modulus, respectively. Non-zero components of the strain

tensor are deﬁned as

∂u

∂r

; ε

∂w

∂z

; γ

∂u

∂z

∂w

∂r

, (7.30)

where ε

,ε

and γ

are radial, hoop, axial and shear strains, respectively.

Corresponding components of the stress tensor are deﬁned as

(1 + ν)(1 − 2ν)



(1 − ν)

∂u

∂r

+ ν



∂w

∂z



; (7.31)

(1 + ν)(1 − 2ν)



∂u

∂r

+(1− ν)

+ ν

∂w

∂z



; (7.32)

(1 + ν)(1 − 2ν)



∂u

∂r

+ ν

+(1− ν)

∂w

∂z



; (7.33)

2(1 + ν)



∂u

∂z

∂w

∂r



. (7.34)

Under a condition of ∂/∂z = 0, (7.28)–(7.34) reduce to 1D problem con-

sidered in [879].

7.2 Stress–Strain State of HTSC in Applied Magnetic Fields 333

Macroscopic electromagnetic phenomena in the HTSC are described by

the Maxwell equations as

∇×E = −∂B/∂t; ∇×B = μ

J; J = J

+ J

, (7.35)

where μ

, E and B are the magnetic permeability in air, the electric and

the magnetic ﬁelds, respectively. The magnetic ﬁeld is caused by the shielding

current J

and the external current J

. A type-II superconductor in a quasi-

static ﬁeld is well described, using the standard critical state model [1024].

Constitutive relationships between the shielding current density J

and the

electric ﬁeld E are obtained from force balance on a vortex as

= J

(|B|)E/|E|, if|E| = 0 ; (7.36)

∂J

/∂t =0, if|E| =0. (7.37)

When the electric ﬁeld E is induced in a local region by change of the mag-

netic ﬁeld from (7.35), shielding currents are induced from (7.36). If there is

no electric ﬁeld by the shielding eﬀect, the situation of currents is not changed

from (7.37). While the critical current density J

has a strong dependence on

−

0.8

0.6

0.4

0.2

0.0

−0.2

1-D Hoop Stress

1-D Radial Stress

2-D Hoop Stress

2-D Radial Stress

r (10

–3

2µ

/ B

∗

0 23.012.5

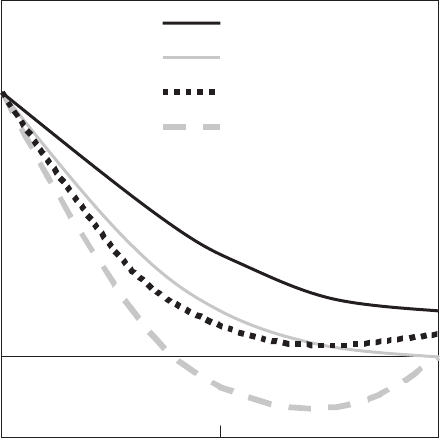
Fig. 7.26. Radial (σ

) and hoop (σ

)stressesvsradialcomponent(atz=0)in1D

and 2D models [1084]

334 7 Modeling of YBCO Oxide Superconductors

0.2

0.1

0.0

−H/2 −H/4 0.0 H/4 H/2

Axis, z

Normalized Strain

(b)

−H/2 −H/4 0.0 H/4 H/2

Axis, z

−

1.0

0.8

0.6

0.4

0.2

0.0

−0.2

−0.4

−0.6

−0.8

−1.0

Normalized Strain

(c)

0.0

−0.2

−

−0.4

−

−0.6

−

−0.8

−

−1.0

−

−1.2

0 R/4 R/2 3R/4

1.9

1.6

0.9

0.3

Normalized Strain

Radius, r

(a)

0.0

0.6

1.3

1.8

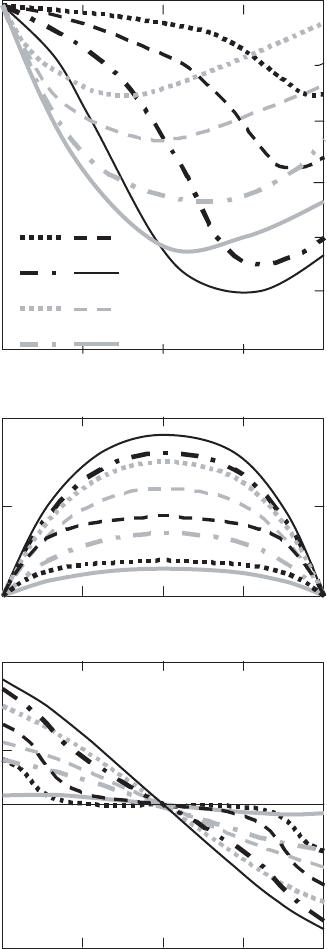
Fig. 7.27. The normalized strains, when the external ﬁeld is reduced from 2.0 to

0.0 T: (a)shearstrains(γ

/γ

max

) on the upper surface of a bulk HTSC; (b)and

(c)hoopstrain(ε

/γ

max

)andshearstrain(γ

/γ

max

) on the side surface of a bulk

HTSC [1085]

7.2 Stress–Strain State of HTSC in Applied Magnetic Fields 335

the magnetic ﬁeld, the Bean model [737]

is applied to the present analysis to

clarify the basic properties of the stress–strain state. Self-consistent solutions

which satisfy the non-linear equations (7.36) and (7.37) can be obtained, using

a numerical iterative technique [1024, 1039, 1083] and the following boundary

conditions: σ

=0onthesidesurfaceofthecylinder(atr = R), and σ

on the upper and lower surfaces of the cylinder (at z = ±H/2). After the

Lorentz force calculation from the shielding current distribution at each time

step [1039], the ﬁnite diﬀerence method is applied to solve (7.28) and (7.29).

In the iterative calculations, using successive over-relaxation method, the dis-

placements u and w are found in by using turns the boundary conditions until

they are converged to deﬁnite value. Then, the strain distributions are calcu-

lated from (7.30), and the stresses depending on the obtained displacements

of u and w are found from (7.31) to (7.34).

Numerical results are obtained for cylinder with the geometrical parame-

ters: R =23.0mm and H =15.0 mm, Young’s modulus and Poisson’s ratio:

E =95.9GPaandν =0.14, respectively. In the Bean model, a standard value

of the critical current density is J

=1.0×10

A/m

[1084, 1085]. Full magne-

tization with ﬁeld cooling is obtained when shielding currents are induced in

the whole volume of the HTSC (this occurs when the external ﬁeld is reduced

from 2.0 to 0.0 T).

Maximum trapped ﬁeld B

∗

in the sample center for 1D and 2D models are

2.9 T and 1.7 T, respectively [1084]). Two-dimensional distributions of the ra-

dial (σ

) and hoop (σ

) stresses in the sample center (at z = 0) are compared

with 1D solutions in Fig. 7.26. The distributions are normalized with corre-

sponding value of B

∗

. Obviously, largest stresses are obtained in the center

of the bulk. Figure 7.27 presents normalized strains on the side, upper and

lower surfaces of the cylinder (all strains are normalized with the maximum

shear strain, γ

max

, when the external ﬁeld is 1.3 T). The distributions change

as the external ﬁeld is reduced from 2.0 to 0.0 T. The large shear strain (γ

)

is obtained by the large Lorentz force between distributed shielding currents

and the large external ﬁeld in the ﬁrst half of the magnetization. After that,

the shear strain distribution reduces as the external ﬁeld is decreased in the

magnetization process.

According to the Bean model [55], for cylindrical body: ∂B

/∂r = const, yielding

a linear variation of B

with the r-coordinate. In the similar Kim model [545,

546], it is assumed that B

∂B

/∂r = const, yielding a parabolic variation of the

function B

(r).

Computer Simulation of HTSC Microstructure

and Toughening Mechanisms

8.1 YBCO Ceramic Sintering and Fracture

It is quite obvious that the spectrum of structure-sensitive properties of

superconducting ceramics is caused directly by essential inhomogeneous

structure, consisting of superconducting grains, secondary phases, pores and

microdefects, as a rule disposed on intergranular boundaries. The microstruc-

ture formation and fracture occur during sintering, causing internal (residual)

stresses, and during the material loading by diﬀerent thermo-mechanical and

electromagnetic ﬁelds. Based on computer simulation, a joint study of sinter-

ing, cooling and fracture of the structure-heterogeneous material [516, 518,

796] allows a prediction and an optimization of superconductor properties de-

pending on the parameters, including composition, heat rate, initial porosity

of material. In Chap. 5 fundamentals of HTSC computer monitoring have been

discussed. In this section, an example of YBa

7−x

gradient sintering is

considered [61], and proper toughening mechanisms are investigated [807]. The

present analysis could be used, in particular, to study heterogeneous mecha-

nism of the YBCO structure formation and to model the cracking processes

in ab-plane.

8.1.1 Sintering Model of Superconducting Ceramic

During gradient sintering up to microstructure formation, there are the fol-

lowing transformations in the material (Fig. 8.1) [61]:

(1) the primary crystallization, which consists of formation and growth of

facetted crystallites of superconducting phase into powder media of the

sample (T ∼ 800–900

◦

C);

(2) the formation of non-superconducting phase around crystallites due to

active local thermo-diﬀusion (T ∼ 900–920

◦

C);

(3) the sample shrinkage and formation of isolated (closed) porosity owing to a

melting of the non-superconducting phase and its following pushing from

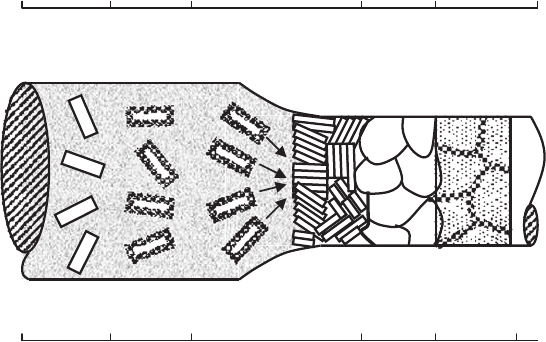
338 8 Computer Simulation of HTSC Microstructure and Toughening

900800

920

960

1000 T, °C

21354

Fig. 8.1. The physical model of microstructure formation of YBCO ceramic during

sintering in thermal gradient. The next process zones are shown of primary crys-

tallization (1); non-superconducting phase formation (2); shrinkage (3); abnormal

grain growth (4) and structure decomposition (5)

aggregates of superconducting crystallites into pores and at the sample

surface (T ∼ 920–940

◦

C);

(4) the secondary re-crystallization, accompanied by breaking of intergranular

buﬀer layers and by creation of big grains with irregular shape (T ∼

960–980

◦

C);

(5) the structure decomposition (T>1000

◦

C).

The proposed computer model generalizes the research results of gradient

sintering of the ferroelectric [516, 518, 796] and YBCO [814] ceramics. It is as-

sumed that temperature in the furnace changes linearly with coordinate. The

modeling consists of successive consideration of following stages: (i) the prop-

agation of a heat front in a powder compact with deﬁnition of temperature

distribution in the sample; (ii) the press-powder crystallization into region of

the sintering temperature that is determined by heat front, in conditions of

the actual gradient sintering of YBCO [61]; (iii) the sample shrinkage with

formation of a closed porosity; (iv) the secondary re-crystallization, which is

an abnormal grain growth under conditions of actual inhibition due to exis-

tence of a mixed secondary phase. In this consideration, the action regions

of the above processes are found by temperature distributions, corresponding

to present physical model. The modeling procedure of the forming HTSC mi-

crostructure during the sample heat has been written in detail in Sect. 5.3,

and the initial parameters, used in computer experiments, are presented in

Table 8.1. The ﬁnite-diﬀerence method is used to solve the ﬁrst main problem

8.1 YBCO Ceramic Sintering and Fracture 339

Table 8.1. Initial parameters used in computer simulation

Parameter Value Unit of measurement

Particle properties

Mean diameter, d 1.5 × 10

−6

Thermal conductivity, λ

18 W/(m K)

Blackness order, ε 1–

Density, ρ 3200 kg/m

Heat capacity, c

0.8 kJ/(kg K)

Air properties

Atmospheric pressure, H 1010 GPa

Thermal conductivity, λ

0.0241 W/(m K)

Adiabatic index, γ 1.4 –

Prandtl criterion, Pr 0.7 –

Accommodation factor, a 0.97 –

Length of molecular free run, Λ

0.65 × 10

−7

for quasi-linear equation of thermal conduction (see Appendix C.1) for zero

initial and corresponding boundary conditions. In this case, the region, con-

sidered in ab-plane, is presented by a 2D lattice with 1000 square cells of char-

acteristic size, δ. Every cell is either a grain nucleus of 123 phase or void. The

cells with the same numbers form corresponding grain or void (see Fig. 8.2).

The secondary re-crystallization is modeled on the basis of the Wagner–

Zlyosov–Hillert’s model of abnormal grain growth [1]. In the YBCO ceramic,

it is caused by admixture phases at intergranular boundaries. As followed from

[61], the material of intergranular buﬀer layers is BaCuO

−CuO system with

inclusions of admixtures. In any time t, the abnormal grain growth occurs

under condition [1]:

|1/R

− 1/R

| >I

/2 , (8.1)

where

j=1

; f

= n

;

j=1

=1;

j=1

= N

;

(8.2)

is the size-class number of the width ΔR, containing n

grains with radius

in j-class of the discrete space (R, t); I

=6f

/(πr) is the inhibition; f

is the volumetric fraction of secondary phase particles; r is the mean radius of

particles. The inhibition, I

, depending on the particle radius and on the frac-

tion of secondary phase, governs abnormal grain growth that allows to deﬁne

the microstructure and strength parameters in dependence on the secondary

phase characteristics.

Assume that mass-transfer from one grain to another occurs according to

the mechanism of normal crystal growth on non-singular surfaces (i.e., the

boundaries with suﬃciently high concentration of steps and demonstrating

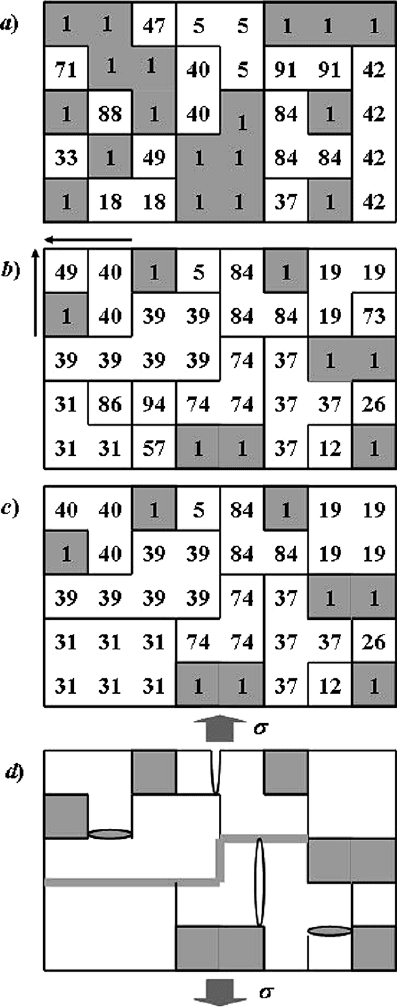
340 8 Computer Simulation of HTSC Microstructure and Toughening

Fig. 8.2. Scheme of 2D fragment of YBCO ceramic structure (ab-plane) in PC: (a)

crystallization (porosity is denoted by 1 and shown by gray color); (b) shrinkage

(arrows show its directions); (c) abnormal grain growth and (d) macrocrack prop-

agation (which is depicted by gray line) into model structure (where white color

shows microcracks formed during the sample cooling, microcracks into process zone

have gray color). Numbers denote a sequence of nucleation of present grain