Островський А.Л. Геодезія. Частина перша. Топографія

Подождите немного. Документ загружается.

Рис.

11.3.3.

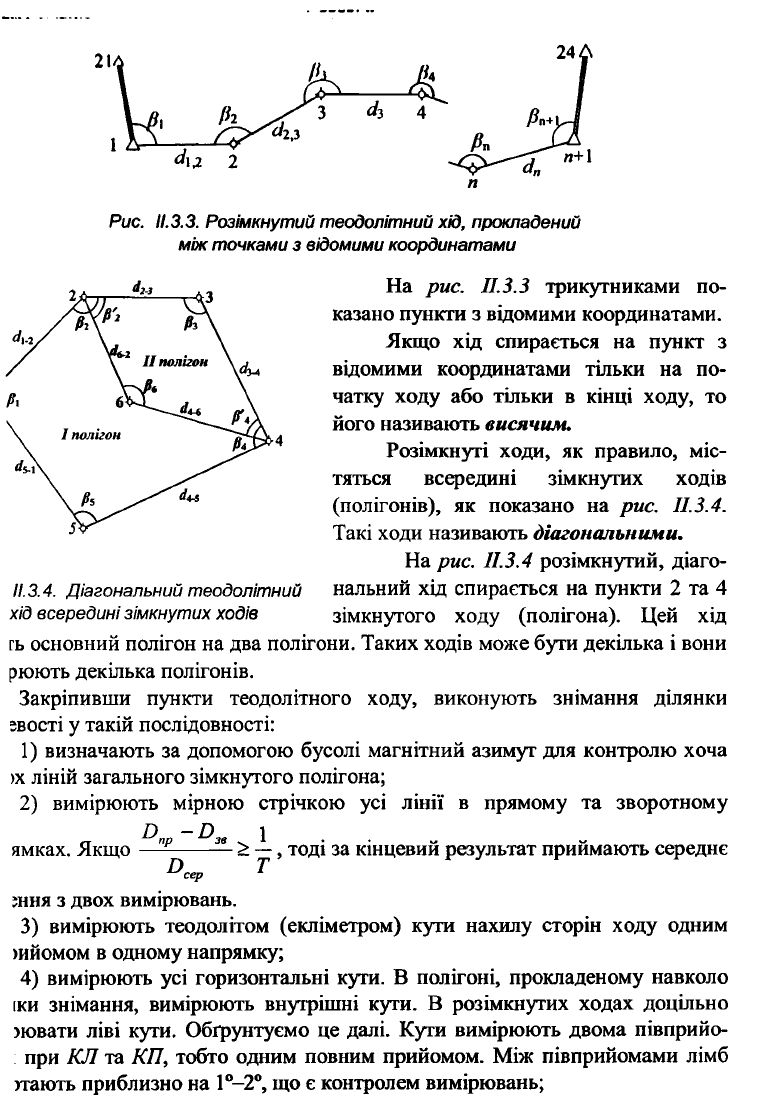
Розімкнутий теодолітний хід, прокладений

між точками з відомими координатами

На рис. II. 3.3 трикутниками по-

казано пункти з відомими координатами.

Якщо хід спирається на пункт з

відомими координатами тільки на по-

чатку ходу або тільки в кінці ходу, то

його називають висячим.

Розімкнуті ходи, як правило, міс-

тяться всередині зімкнутих ходів

(полігонів), як показано на рис. II. 3.4.

Такі ходи називають діагональними.

На рис. 11.3.4 розімкнутий, діаго-

нальний хід спирається на пункти 2 та 4

зімкнутого ходу (полігона). Цей хід

гь основний полігон на два полігони. Таких ходів може бути декілька і вони

рюють декілька полігонів.

Закріпивши пункти теодолітного ходу, виконують знімання ділянки

гвості у такій послідовності:

1) визначають за допомогою бусолі магнітний азимут для контролю хоча

>х

ліній загального зімкнутого полігона;

2) вимірюють мірною стрічкою усі лінії в прямому та зворотному

і . . „

ямках. Якщо — > —, тоді за кінцевии результат приймають середнє

Deep Т

;ння з двох вимірювань.

3) вимірюють теодолітом (екліметром) кути нахилу сторін ходу одним

>ийомом в одному напрямку;

4) вимірюють усі горизонтальні кути. В полігоні, прокладеному навколо

іки знімання, вимірюють внутрішні кути. В розімкнутих ходах доцільно

мовати ліві кути. Обґрунтуємо це далі. Кути вимірюють двома півприйо-

при KJI та КП, тобто одним повним прийомом. Між півприйомами лімб

угають приблизно на 1°-2°, що є контролем вимірювань;

II.

3.4. Діагональний теодолітний

хід всередині зімкнутих ходів

Гори іінітипі.іні інімшінн

S) виконують 'інімання ситуації. Знімання ситуації можна виконувати

одночасно з прокладанням теодолітних ходів, що доцільніше, або окремо після

прокладання ходів.

11.3.2.

Способи знімання ситуації. Зарис

Як уже зазначалося, знімання ситуації доцільно виконувати одночасно з

прокладанням теодолітного ходу. Під час вимірювання ліній в прямому

напрямку за допомогою мірної стрічки, рулетки, екера та теодоліта виконують

знімання ситуації. Результати знімання записують олівцем на схематичному

писунку, який називається зарисом. На ньому викреслюють схематично

ситуацію території, яку знімають, назви угідь, характеристики об'єктів тощо.

Нехай вимірюють лінію між пунктами 1 і 2 теодолітного ходу (рис. 11.3.5).

Для цього послідовно укладають стрічку вздовж лінії 1-2. У точці а на відділі

37,15 м від пункту 1 лінія 1-2 перетинає межу між лісом та луками. Резульїаі

записують на зарисі (рис. ІІ.З.5).

Потім, опустивши з рогу будинку С перпендикуляр на лінію 1-2 (точка б),

вимірюють віддаль від пункту 1 до

основи перпендикуляра (70, 20 м), а

рулеткою вимірюють довжину цього

перпендикуляра (12,12 м). Потім

опускають перпендикуляри на лінію 1-2

теодолітного ходу з рогів будинку В і А

(точки в і г відповідно), вимірюють від

пункту 1 теодолітного ходу відстані до

основ цих перпендикулярів та за

допомогою рулетки довжини цих пер-

пендикулярів. Усі ці виміри записують на

зарисі. Такий спосіб знімання

називається способом перпендикулярів.

Короткі перпендикуляри (до двох метрів)

будують на око, довші - за допомогою

екера. В точках д і е лінію 1-2 перетинає

фунтова дорога. На зарисі записують

нйідалі від пункту 1 до перетину цією

лінією ґрунтової дороги.

24-

чагарник

Рис.

11.3.5.

Зарис знімання ситуації

способом перпендикулярів

183

ГІИІІВІ II

11.4. Камеральні роботи у горизонтальному зніманні

Під камеральними роботами в топографії розуміють роботи, що вико-

тоть не в полі, а в приміщенні. Це переважно обчислення (опрацювання

зультатів знімання) та креслення. Результат цих робіт - ситуаційний план

сцевості.

11.4.1.

Залежність між дирекціонами кутами

та горизонтальними кутами теодолітного ходу

Знаючи залежність між дирекційними та горизонтальними кутами

адолітного ходу, можна обчислити дирекційні кути усіх ліній ходу, якщо

(омий дирекційний кут хоча б однієї лінії.

Припустимо, що відомий дирекційний кут лінії 1-2 а,_

, а в пункті 2 ходу

міряно правий за ходом горизонтальний кут Р

(рис. II. 4.1). Продовжимо

іію 1-2. Оскільки показані на рис. ІІ.4.1 напрямки на північ (Пн) - паралельні

к собою і паралельні до осьового меридіана деякої зони, то продовжена лінія

: у точці 2 також має дирекційний кут а,_

. З рисунка видно, що, додавши до

)го кута 180°, отримаємо дирекційний кут а

_, лінії 2-1. Якщо ж від а

няти виміряний правий горизонтальний кут Р

, то одержимо дирекційний

•

лінії 2-3 а

_з, тобто

«2-3 = «1-2 +

180

'-Рп- (

)

Узагальнюючи цю формулу, сформулюємо її так: щоб отримати

(ЄКЦІЙНИЙ кут наступної сторони теодолітного ходу, потрібно до дирек-

ного кута попередньої сторони додати 180° і відняти виміряний правий за

ходом горизонтальний кут повороту ходу.

Використовуючи формулу (ІІ.4.1),

знайдемо дирекційні кути усіх сторін

ходу. В розімкнутих теодолітних ходах

часто вимірюють ліві за ходом гори-

зонтальні кути р

. Знайдемо залежність

між дирекційними кутами та виміряними

лівими відносно напрямку ходу

горизонтальними кутами. Зв'язок між

правими і лівими за ходом горизон-

тальними кутами виражається формулою

=Ш°-Р

. (ІІ.4.2)

Пн

11.4.1. Визначення дирекційного

/та

а2-з

за відомим дирекційним

пом

Of.2

та виміряним правим по

оду горизонтальним кутом р

Гортонтічп.но знімання

Підставивши (ІІ.4.2) у формулу (11.4.1), одержимо

«2-ї = «І

" - (

360

" - Pjl )

або

«2-3 =«1-2 +Рл -180°. (И.4.3)

Тобто, щоб отримати дирекційиий кут наступної сторони теодолітного

ходу, потрібно до дирекційного кута попередньої сторони додати виміряний

піний за ходом горизонтальний кут повороту ходу і відняти 180°.

Треба пам'ятати, що дирекційний кут може набувати значення від 0° до

Я60*. Якщо в результаті обчислень за формулою (ІІ.4.1) або (И.4.3) отримаємо

від'ємне значення дирекційного кута, тоді до результату потрібно додати 360",

а якщо одержимо значення більше за 360°, то відняти 360°.

Оскільки усно простіше виконувати дію додавання, ніж віднімання (віднімані

180° простіше, ніж виміряні горизонтальні кути), то в розімкнутих ходах переважно

вимірюють ліві за ходом горизонтальні кути. Звичайно, якщо обчислюють «а

допомогою калькулятора або комп'ютера, то це не має значення.

11.4.2.

Врівноваження горизонтальних кутів у полігоні

Наведемо просте виведення формули теоретичної суми внутрішніх кугів

Оагатокутника. Нехай маємо багатокутник (рис. ІІ.4.2). Позначимо приблизно

посередині цього багатокутника точку О, з'єднаємо її з усіма вершинами

баг атокутника (в нашому випадку и-кутника). Утвориться стільки трикутників,

скільки є сторін в багатокутнику. Отже, вершин, сторін та трикутників буде п.

Гума кутів в окремому трикутнику дорівнює 180°. Загальна сума кугів

становитиме 180°

•

п. Але сума кутів навколо центральної точки, яка дорівнює

360° =180°-2, не входить в суму кутів при вершинах «-кутника. Тому

теоретичну суму внутрішніх кутів при вершинах и-кутника можна обчислити як

^ /З

= 180°и -360°= 180° и -180°2 = 180°(п-2) .

Отже, для зімкнутого багатокутника теоретичну суму внутрішніх кутів

(находять за формулою

£/J

=180°-(«-2).

(II

.4.4)

Якщо виміряно усі внутрішні кути у вершинах и-кутника, можна отримати суму

" л

цих кутів, яку називають практичною сумою кутів і позначають ^Г /}

пр

Різниця між практичною і теоретичною сумою виміряних кутів називається

нев'язкою. Її прийнято позначати . Обчислюється нев'язка за формулою

185

Розділ II

/*=ІАФ-ІА- (и-

)

і і

Як відомо, виміри спотворені

похибками. У розділі ІІ.2.6 виведена

формула (ІІ.2.22) для розрахунку

допустимої нев'язки кутів, виміряних

технічними теодолітами. Формула для

полігонів має вигляд don.f

= l'-Jn .

Для полігона на рис.

11.4.3

п = 8,

отже, don.fp = 14/8 = 2,8'.

Якщо fp < don.fp, то переходить

до врівноваження горизонтальних

кутів. Якщо ж fp > don.fp, шукають

похибку в обчисленнях горизонтальних кутів або повторно вимірюють

горизонтальні кути.

Під врівноваженням кутів розуміють введення в кути поправок з тим, щоб

сума врівноважених кутів дорівнювала теоретичній сумі кутів.

Наведемо основні правила врівноваження горизонтальних кутів у тео-

долітному ході:

1. Поправки в кути вводять за допомогою, рівномірно до кількості кутів і

зі знаком, протилежним, до знака нев'язки.

2. їх значення заокруглюють до 0,5' і вводять у виміряні кути так, щоб

значення врівноважених кутів були без десятих часток мінути.

3. В кути, утворені короткими лініями, додають більші поправки.

4. Сума поправок у виміряні кути має дорівнювати кутовій нев'язці з

протилежним знаком.

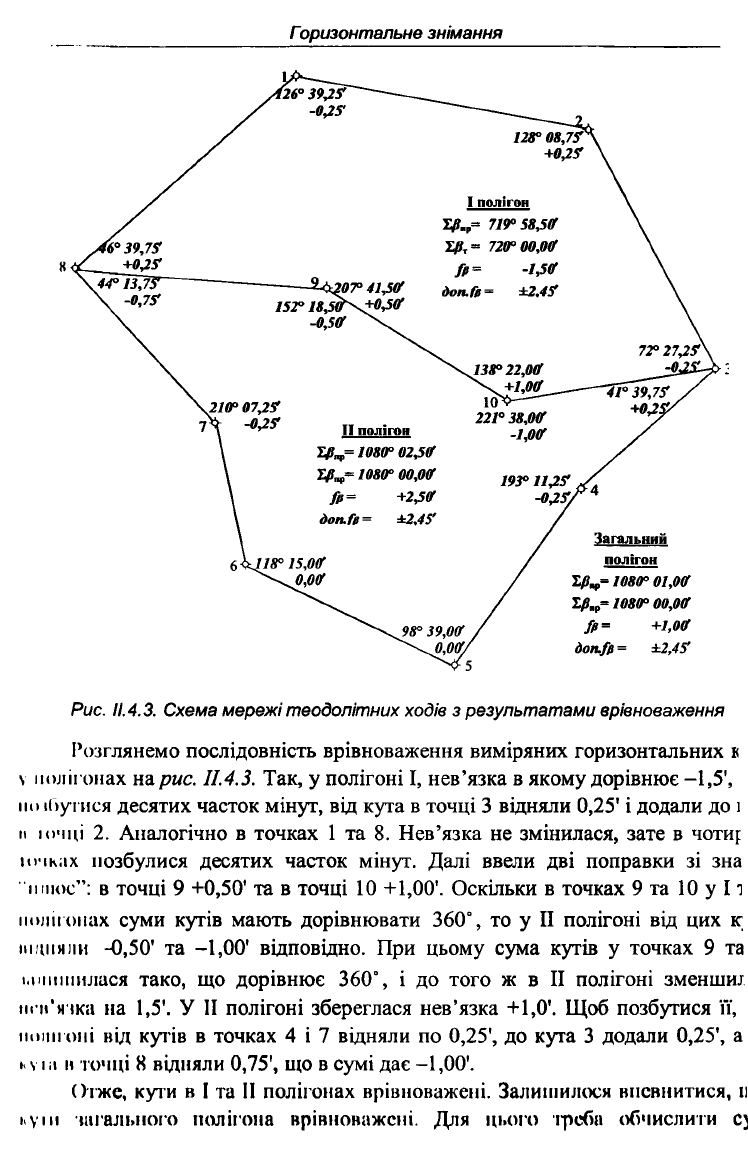
Розглянемо мережу теодолітних ходів, які утворюють два полігони ( рис.

11.4.3). На схемі вказано виміряні горизонтальні кути, обчислені суми горизон-

тальних кутів загально та в І і II полігонах, обчислені нев'язки та допустимі

нев'язки горизонтальних кутів у полігонах. Дуже важливим є контроль

правильності обчислення кутових нев'язок. Для цього є контрольна формула: сума

нев'язок окремих полігонів має дорівнювати нев'язці загального полігона, тобто

Лл+Л.и- (ІІ.4.6)

Якщо умова (ІІ.4.5) не виконується, то необхідно ще раз перевірити обчислення.

На рис. 11.4.3 /^=+1,0'; Д,=-1,5'; /

МІ

= 2,5', тоді -1,54-2,5'= 1,0'.

Отже, контроль обчислень виконано.

Рис.

11.4.2.

До виведення формули

теоретичної суми кутів п трикутників

1Ш)

Горизонтальнв знімання

Рис.

11.4.3.

Схема мережі теодолітних ходів з результатами врівноваження

Розглянемо послідовність врівноваження виміряних горизонтальних 8

v полігонах на рис. ІІ.4.3. Так, у полігоні І, нев'язка в якому дорівнює -1,5',

по іПугися десятих часток мінут, від кута в точці 3 відняли 0,25' і додали до і

м ю'щі 2. Аналогічно в точках 1 та 8. Нев'язка не змінилася, зате в чотир

німках позбулися десятих часток мінут. Далі ввели дві поправки зі зна

ІІПІОС": в точці 9 +0,50' та в точці 10 +1,00'. Оскільки в точках 9 та 10 у І

полігонах суми кутів мають дорівнювати 360°, то у II полігоні від цих к

мпщиіш -0,50' та -1,00' відповідно. При цьому сума кутів у точках 9 та

мнішшлася тако, що дорівнює 360°, і до того ж в II полігоні зменшш

іи іГязка на 1,5'. У II полігоні збереглася нев'язка +1,0'. Щоб позбутися її,

поіпгоні від кутів в точках 4 і 7 відняли по 0,25', до кута 3 додали 0,25', а

• via и точці 8 відняли 0,75', що в сумі дає -1,00'.

Отже, кути в І та II полігонах врівноважені. Залишилося впевнитися, її

і'уіи загального полігона врівноважені. Для цього треба обчислити cj

•пранок її куш штильного полігона. Ци сума ііониііііа дорівнювати І',

кільки нсн'яіка н загальному полігоні становить-1-І'.

В кути загального полігона внесено такі поправки:

куги 1 2 3

4 5

6 7

8 сума

поправки

-0,25' +0,25' 0,00'

-0,25' 0,00'

0,00' -0,25'

-0,50' -1,00'

Зауважимо, що під час обчислення дирекційних кутів усіх ліній вико-

стовують не виміряні, а врівноважені кути.

11.4.3.

Врівноваження горизонтальних кутів

у розімкнених теодолітних ходах

Нехай маємо теодолітний хід, прокладений між пунктами з відомими

ординатами (рис. II. 4.4).

Р, П 23

[121

Рис.

11.4.4. Теодолітний хід,

прокладений між пунктами з

відомими

координатами

Використовуючи формули залежності між дирекційними кутами та

ами повороту (ІІ.4.1) та (ІІ.4.3), запишемо відповідно:

для лівих кутів

п+1

«,=«-+ IX -180°

•

Г« + U; (ІІ.4.7)

для правих кутів

л+1

сс

=а„+т°(п + 1)-^Р„.

(II 4.8)

Розв'яжемо формули (ІІ.4.7) та (ІІ.4.8) відносно теоретичних сум

изонтальних кутів

л+1

Z йітеор = «к -

сс„

+180°

•

(я +1); (11-4.9)

л+1

Х^Птеор

=0С

п ~

к +180° (и + 1).

Знайдемо для розімкнутого ходу нев'язки. Так, для лівих кутів

л+1

fp Л

~ И^лпр ^Рптеор

(П.4.10)

(И.4.11)

і приюнтяпння інімпння

її jvія праних

/ЛЯ'І^.ПФ-ZA.tcop- (Н-4.12)

і і

За формулами (ІІ.4.9) та (ІІ.4.10) можна знайти теоретичні суми

розімкиугих теодолітних ходів, а за формулами (ІІ.4.11) та (11.4.12) нев'язки в

цих ходах і тільки після цього врівноважити горизонтальні кути.

Правила врівноважування горизонтальних кутів у розімкнутих теодо-

літних ходах точно такі самі, як і правила врівноважування горизонтальних

кугів у зімкнутих ходах (полігонах).

11.4.4.

Пряма та обернена геодезичні задачі

1. Пряма геодезична задача.

Нехай відомі прямокутні координати точки 1 (хі,.уі), довжина лінії 1-2 Л'і

а дирекційний кут цієї лінії а,_

(рис. 11.4.5).

Необхідно знайти: координати

очки 2 (х2,уг) •

На рис. 11.4.5 показана

прямокутна система координат ХОУ, в

якій розміщені точки 1 та 2.

Через точку 1 проведемо пряму,

іаралельну до осі ОХ. Тоді в точці 1 ця

пряма з лінією 1-2 утворить кут се,_

який і є дирекційним кутом лінії 1-2.

Спроектуємо точку 2 на осі координат. В

результаті проектування утвориться пря-

мокутний трикутник 1-С-2. Тоді, як вид-

но з рисунка, координати точки 2, тобто

л'2 та у2, більші за координати точки 1

відповідно на катети 1-С та 2-С. Ці

катети позначимо Ах та Ау. їх називають приростами координат.

Пезпосередньо з трикутника 1-С-2 можна записати

А* АУ • /II л пч

= cosa

; — = sma

. (11.4.13)

^1-2 $1-2

Або

Ax = 5,_

•

cos а,_

; Ay = S,_

•

sin a,_

. (II.4.14)

Знаючи прирости координат, знайдемо координати точки 2

=х, +AX =

JC,

cosa,_

; (11.4.15)

+Ay = y

+ S^ sin a,_

. (H.4.16)

Рис.

11.4.5.

Пряма та обернена

геодезичні задачі

189

Ч формул (11.4.15) іа (11.4.16) очемидио, що координат наступної точки

у дорівнюють координатам попередньої точки ходу нлюс значення

рості» координат між цими точками.

Розв'язуючи цю задачу багаторазово, можемо обчислити координати усіх

зк мережі теодолітних ходів. Для цього достатньо знати координати однієї

<и, довжини усіх ліній мережі та дирекційні кути цих ліній.

2. Обернена геодезична задача.

Нехай відомі прямокутні координати точок

та 2 (х\,у\,х

,у2)

(рис.

II. 4.5).

Потрібно знайти: довжину лінії Si.2 між цими точками та дирекційний кут

цієї лінії.

Спочатку знайдемо прирости координат Ах та Ау. З рис. II. 4.5 очевидно, що

4У=Уг~Ух-

З прямокутного трикутника 1С2 можемо записати

Ьу _У

~ Ух

tg «!-2 =

Ах

Звідси

а,_

= arc tg

-У,

у х

—

X, J

(11.4.17)

(11.4.18)

(11.4.19)

(11.4.20)

Але насправді знаходимо не дирекційний кут, а румб цієї лінії г,_

. Як

ло, значення дирекційного кута залежить від знаків приростів координат,

даємо, що в першій чверті Ах, Ау мають додатні знаки, дирекційний кут і

і мають однакові значення, тобто а = г ; в другій чверті Ах має знак

ус»; Ау - «плюс» і а = 180-г; у третій - обидва прирости координат Ах,

іають від'ємні знаки і а = г +180 і в четвертій - Ах має знак «плюс», Ау -

«мінус» і а = 360 - г.

Відстань

Si_2

визначають з контролем з цього самого трикутника, викорис-

очи формули (ІІ.4.13). Отже,

Ах Ау

cos а,_

sin а,_

= yjAx

+Ау

(ІІ.4.21)

Обернену геодезичну задачу зазвичай розв'язують, щоб знайти вихідні

сційні кути, коли відомі тільки вихідні (початкові) координати двох точок,

)ж для розв'язку різних інженерно-геодезичних завдань.

11.4.5.

Врівноваження приростів координат

у зімкнутому теодолітному ході

З геометрії відомо, що сума проекцій зімкнутої ламаної лінії на будь-яку

инатну вісь дорівнює нулю. Щоб зрозуміти суть цієї теореми, достатньо

Гпри іонтппі.ііо -.інімпнн»

спроектувати на осі координат сторони

ірнкушика, які також є зімкнутими

маминими лініями (jmc. 11.4.6). Як бачимо

з рисунка, JC,>х

,х

>х,та х

<х

. Тому

прирости координат Ах

_,, Ас,_

- додатні

величини, а Дх

- від'ємна. Отже,

Ї;А*=О,

2>=о.

(ІІ.4.22)

(И.4.23)

Але ці умови виконуються, якщо

довжини сторін багатокутника виміряні

безпомилково. Однак під час вимірю-

вання ліній похибки вимірювань є неми-

нучими, тому суми приростів координат

не дорівнюватимуть нулю.

Додавши обчислені прирости коор-

динат, отримаємо деякі величини —

нев'язки приростів координат:

-Ауц

Рис.

11.4.6.

Проектування зімкнутого

багатокутника на осі координат

/д*

Л,=2>-

(ІІ.4.24)

(ІІ.4.25)

Рис.

11.4.7.

Геометричнийзміст

нев'язок приростів координат

у зімкнутому полігоні

Тобто трикутник не буде зімкнутою

фігурою. Під час його побудови від точки

І замість точки 2 отримаємо точку 2', а

замість точки 3 - точку 3', і, нарешті,

замість точки 1, з якої починали

побудову, одержимо точку 1' (рис. 11.4.7).

Тобто трикутник не зімкнеться на величину

нев 'язкою теодолітного ходу.

Лінійна нев'язка - це гіпотенуза прямокутного трикутника, катети якого с

нев'язками та /

по осях координат. Тому

яка називається ліншною

fs = y[f<

+ f

At ^ J by

(ІІ.4.26)

Обчислену за формулою (ІІ.4.26) лінійну нев'язку порівнюють з допус-

тимою. Нев'язку вважають допустимою, якщо вона не перевищує 1:2000

довжини периметра за середніх умов вимірювання ліній; 1:3000 - за

191