Островський А.Л. Геодезія. Частина перша. Топографія

Подождите немного. Документ загружается.

Розділ II

ЇИННИКОВОЮ стрілкою обводять фігуру. На дисплеї висвічується значення

міряної площі. Якщо фігуру обводять проти годинникової стрілки, на дисплеї

свічується від'ємне значення площі. Цю особливість можна використовувати,

що всередині вимірюваної площі є інші фігури. При цьому планіметр

тематично віднімає площу або площі фігур всередині основної фігури.

відліковий пристрій

uc.

11.5.4.

Будова цифрового планіметра Рис.

11.5.5.

Будова цифрового планіметра

Якщо площа фігури надто велика, то її вимірюють, поділивши її на

екілька менших сегментів. Для цього спочатку обводять контур першого

егмента і натискають клавішу HOLD, далі обводять контур другого сегмента і

нову натискають HOLD. Ті самі дії повторюють для решти сегментів. В

езультаті на дисплеї одержують сумарне значення площі. Якщо воно

іеревищує кількість символів на дисплеї відлікового пристрою планіметра, то

диниці вимірювання змінюватимуться автоматично, наприклад, з квадратних

антиметрів на квадратні метри.

Ту саму площу можна виміряти декілька разів. Після кожного вимірю-

іання натискають клавішу END, а після останнього - натискають клавішу

WER й одержують кінцевий усереднений результат.

Точність вимірювання площ цифровими планіметрами в середньому в 1,5

>аза вища порівняно з механічними і залежить в основному від точності

)бведення контуру фігури.

PLANIX 5 PLANCOM KP-90N

>12

І оризонтальнв знімання

11.5.5.

Функціональні можливості й технічні характеристики

цифрових планіметрів

Функціональні можливості циф-

рових планіметрів такі:

• вибір метричної або анг-

лійської систем вимірювань;

вибір одиниць вимірювань:

мм

одиниць

см

, м

, км

у метричній системі

•

іГю

дюймів, квадратних футів і акрів - в

англійській системі вимірювань;

• вимірювання площ у змен-

шених або збільшених масштабах;

• вимірювання площ з різними

масштабами;

• фіксування у пам'яті значення

площі виміряної фігури;

• додають площі декількох сег-

ментів у межах однієї фігури;

• обчислення середнього зна-

чення з вимірів тієї самої площі;

• запит масштабного коефі-

цієнта (коли масштаб карти - 1/N, то N

запам'ятовується як масштаб);

• вимірювання площ із пульсу-

ючого відліку (якщо не було

встановлено одиницю вимірювання).

Найсучасніші моделі цифрових

планіметрів, такі як PLANIX ЕХ (рис.

II. 5.6), PLANIX S10 marble (фірма-

виробник TAMAYA TECHNICS INC.,

Японія), PLANCOM КР-21С (рис.

11.5.7) (фірма - виробник PLANCOM,

Японія), Ushikata Х-Р1ап 380 dill (рис.

П.5.8), не тільки обчислюють площі, але

й вимірюють:

• довжини прямих ліній і

кривих,

Рис.

11.5.6.

Загальний вигляд

цифрового планіметра PLANIX ЕХ

кя

Рис.

11.5.7.

Загальний вигляд

цифрового планіметра

PLANCOM КР-21С

Рис.

11.5.8.

Загальний вигляд

цифрового планіметра

Ushikata Х-РІап 380 dill

213

Розділ

• обчислюють координати, кути, радіуси кіл, дуги, причому координати

ожуть бути одержані з урахуванням реального масштабу карти.

Такі моделі, як PLANIX ЕХ та PLANCOM КР-21С, також можна

ід'єднати до комп'ютерів і отримувати файл координат. Друкують результати

а спеціальних принтерах, які безпосередньо під'єднані до планіметра.

Нижче в табл. ІІ.5.1 наведено основні характеристики найпоширеніших в

рактиці типів цифрових планіметрів.

Таблиця II. 5.1

Технічні характеристики цифрових планіметрів

PLANIX 5

PLANIX 7

PLANIX ЕХ

Тип

планіметра

полюсний роликовий

роликовий

Дисплей LCD

8 символів х

1 рядок

8 символів х 1 рядок

17 символів х 3 рядки

Діапазон

вимірювань

діаметр 35,6 см

300 см х 30 см

380 ммх 10 м

Точність

не нижче за ±

0,2 %

не нижче за ± 0,2 %

±0,1 %

Одиниці

вимірювання

см

2 2 2

см м км га

мм

см

км

га

Габарити/

Вага

64 х 213 x39 мм

/900 г

150x240x39 мм / 500 г

350 х 165 х 43 мм

/ 1000 г

11.5.6.

Теорія полярного планіметра

Спростимо зображення планімет-

ра, як це зроблено на рис. II. 5.9. Нехай

=R - обвідний важіль; ОА

полюсний важіль; А„ - точка з'єднання

цих важелів; В

- точка, якою обводять

контур; О - полюс планіметра. Від-

ліковий механізм на рис. II. 5.9 зо-

бражено потовщеним штрихом, від-

даленим від точки А

на відстань г.

Відрізок г є продовженням обвідного

важеля А

. Нехай обвідна точка В„

суміщена з точкою криволінійного

контуру, а початковий відлік від-

лікового механізму становить т„. До-

пустимо, що обвідний важіль дещо

Рис.

II. 5.9.

До розгляду теоріі

полярного планіметра

>214

І оризонтальнв знімання

переміститься паралельно до початкового положення і займе нове положення

Л|В'. При цьому механічне колесо відлікового механізму повернеться на

величину h, обвідна точка з точки В

переміститься в точку В', а точка А„ опише

дугу А„Аі радіусом кола R. Оскільки h - дуже мала величина, відрізок

вважатимемо прямою.

Далі припустимо, що обвідний важіль повернеться навколо точки А, на

незначний кут а, і займе положення АіВь Водночас лічильне колесо

відлікового механізму повернеться в протилежному напрямку на дугу га,. Між

початковим положенням важелів ОАВ і новим ОА|В] розташована площа Р|. Цс

: юіца паралелограма А

В'Аі та двох кругових секторів з радіусами R та R|.

< К

кільки площа першого сектора АіВ'В, - ASi = 0,5R

ai , другого - AS..

0.5-R,

-p, і площа паралелограма AS3 = Rh, тоді

=R-h + -|(R

-a

+ R?-р,). (II.5.1)

Під час описаних переміщень важелів відлікове колесо лічильного

механізму пройшло шлях h - гаї. Якщо позначити одну поділку планіметра І,

нка дорівнює 1/1000 частині від довжини ободу відлікового колеса і, якщо

початковий відлік піл, а новий відлік ш

тоді шлях, який пройшло лічильне

колесо, буде t-(mn -m,). Тому

—

гаї = t-(mn-mi). (II.5.2)

Звідси

h = t (mn - mi) + га

(ІІ.5.3)

Отже, площа паралелограма дорівнює

= Rt(m

-m,) + RTa,. (II.5.4)

Площу елементарної фігури ОАпВпВТЗіАіО знайдемо як суму площ

паралелограма та двох кругових секторів. Тобто

Р, = R t (mn - mi) + R r ai + 0,5 R

a, + 0,5 R,

p,. (II.5.5)

Площа всієї фігури дорівнюватиме

Р = Rt(m

- m,) + Rrai + 0,5R

a, + 0,5-R,

p, +

Rt(m, - m

) + Rra

+ 0,5R

+ 0,5R,

+ у (11.5.6)

Rt(m

- rrvO + Rra

+ 0,5-R

+ 0,5Ri

-p

Звідси знайдемо

P = Rt-(m

-m

) + RrZa

+ 0,5R

+ 0,5R,

ip„ ^ (II.5.7)

и m„, m

- відповідно початковий та кінцевий відліки планіметра, тобто відліки

планіметра до та після обведення контуру.

Залежно від того, всередині чи ззовні фігури полюс, можливі два

випадки:

214

Розділ II

Перший випадок. Якщо полюс планіметра всередині фігури, площу якої

шзначають, то важіль, описавши коло після обведення контуру, знову

ювернеться в початкове положення. При цьому Іа = ір = 2-к і формула (ІІ.5.7)

чабуде вигляду

Р = R-t-(m

- ш

) + 2-7tR-r + + л-R,

. (ІІ.5.8)

Позначимо:

Rt = x, (II.5.9)

2-TiRr + JtR

i + я-R,

= Q. (II.5.10)

Тоді формулу (II.5.8) запишемо у вигляді

Р = r(m

- ш

) + Q. (11.5.11)

Другий випадок. Полюс розміщений ззовні контуру, який обводять. Тоді

La = 0 і

Б(3

= 0. У такому разі формула (II. 5.11) матиме вигляд

Р = т-(ш

-ш„). (II.5.12)

Отже, площа виміряна планіметром, визначається за формулами (II.5.11)

га (ІІ.5.12).

11.5.7.

Гзометричний зміст сталих планіметра Т і Q

Оскільки т = R-t, де R - довжина обвідного важеля, a t = 1/1000 ободу

лічильного колеса, то добуток R-t можна зобразити у вигляді прямокутника зі

. R ,

сторонами t і R. t = 1 /1000 І І

Отже, планіметр з полюсом ззовні контуру перетворює площу будь-якого

контуру на площу прямокутника зі сторонами t і R. Різниця (т

- т

) у формулі

(ІІ.5.12) вказує на кількість таких прямокутників у площі контуру.

Розглянемо тепер геометричний зміст сталої Q, розвернувши важелі

планіметра під таким кугом ер, щоб площина лічильного колеса проходила через

точку О - полюс планіметра.

Тобто планіметр в першому випадку перетворює будь-яку площу на площу

прямокутника і кола радіусом р, а в другому випадку - тільки на площу пря-

мокутника. Як визначаються сталі планіметра т і Q, описано в пункті ІІ.5.2.

11.5.8.

Перевірки планіметра

Перед використанням полярного планіметра треба перевірити, чи

виконуються такі умови;

1. Лічильне колесо планіметра повинно вільно, без коливань обер-

татися на своїй осі Цього досягають регулюванням гвинтів підшипників,

попередньо попустивши його закріплювальні гвинти. Після регулювання та

закріплення гвинтів між краями лічильного колеса і верньєра має бути

проміжок, у який можна вставити аркуш тонкого паперу.

>216

І оризонтальнв знімання

2. Площина обода лічильного

колеса мас бути перпендикулярна до

осі обвідного важеля.

Для перевірки (див. рис. II.5.10)

обводять той самий контур двічі за

різних положень відлікового пристрою

(ліворуч і праворуч від полюса).

Якщо отримані значення площ в

поділках планіметра різнитимуться

>і

іі.ше ніж на 1/200 від їх середнього

арифметичного, то площу завжди слід

визначати при двох положеннях від-

чікового механізму і за кінцевий результат приймати середнє арифметичне з

цих вимірів.

Рис.

11.5.10.

До перевірки положення

відлікового механізму планіметра

11.5.9.

Точність визначення площ планіметром

Як було показано раніше, стала планіметра т дорівнює т = R-t. Цей

юбуток є площею прямокутника на папері (на плані). Якщо масштаб плану

гановить М, тоді

= т-М

= R-t-M

, (II.5.13)

и' I'd - площа на поверхні Землі, що відповідає сталій планіметра.

Тоді площа Р виміряної ділянки дорівнюватиме

Р = Р

-(Шк -

Шп)

= Rt-M'-K - m„). (И.5.14)

На основі (II.5.14) можемо записати

-m

(И.5.15)

R-t-M

де (т

- т

) - площа в поділках планіметра.

Отже, площа в поділках планіметра прямо пропорційна до площі Р, що

визначається, і обернено пропорційна до квадрата знаменника масштабу плану.

Інакше кажучи, площу визначають планіметром тим точніше, чим вона більша,

і особливо зростає точність зі зменшенням знаменника масштабу плану.

Нагадаємо: масштаб плану (карти) більший, коли знаменник масштабу плану

(карти) менший.

Як видно з формули (ІІ.5.15), малі площі треба визначати за як

найменшого значення R. Довжину обвідного важеля можна змінювати, перс

суваючи полюсний важіль з відліковим пристроєм вздовж обвідного важеля

Змінюючи довжину R, можна змінити ціну поділки планіметра Р

на зручну для

обчислення величину.

217

Розділ II

Площі вузьких, видовжених контурів (дороги, річки, канави тощо)

точніше знаходити геометричним методом, а не планіметром. Найточніше

планіметром визначаються площі контурів, близьких до круглої форми.

Точність вимірювання площ планіметром також залежить від влас-

тивостей основи плану (креслярський папір, калька, пластик, фотоплан). На

кальці, наприклад, лічильне колесо планіметра може ковзати, не повертатися,

що зменшує точність вимірювання планіметром. Можна вважати, що для площ

розміром в середньому 15 см

на папері планіметр забезпечує відносну похибку

1:400, якщо стан приладу добрий. Похибка визначення площі планіметром не

повинна перевищувати принаймні 1:200 від величини площі. Для забезпечення

точної роботи планіметра проф. А.В. Маслов запропонував ставити на

планіметрі два відлікові механізми. Це дало змогу підвищити точність

визначення площі планіметром майже в 1,5-2 рази.

2г,

/ І

/ 1

~У>

і 1

1*1

1*3

У і

У2 У4

Уз

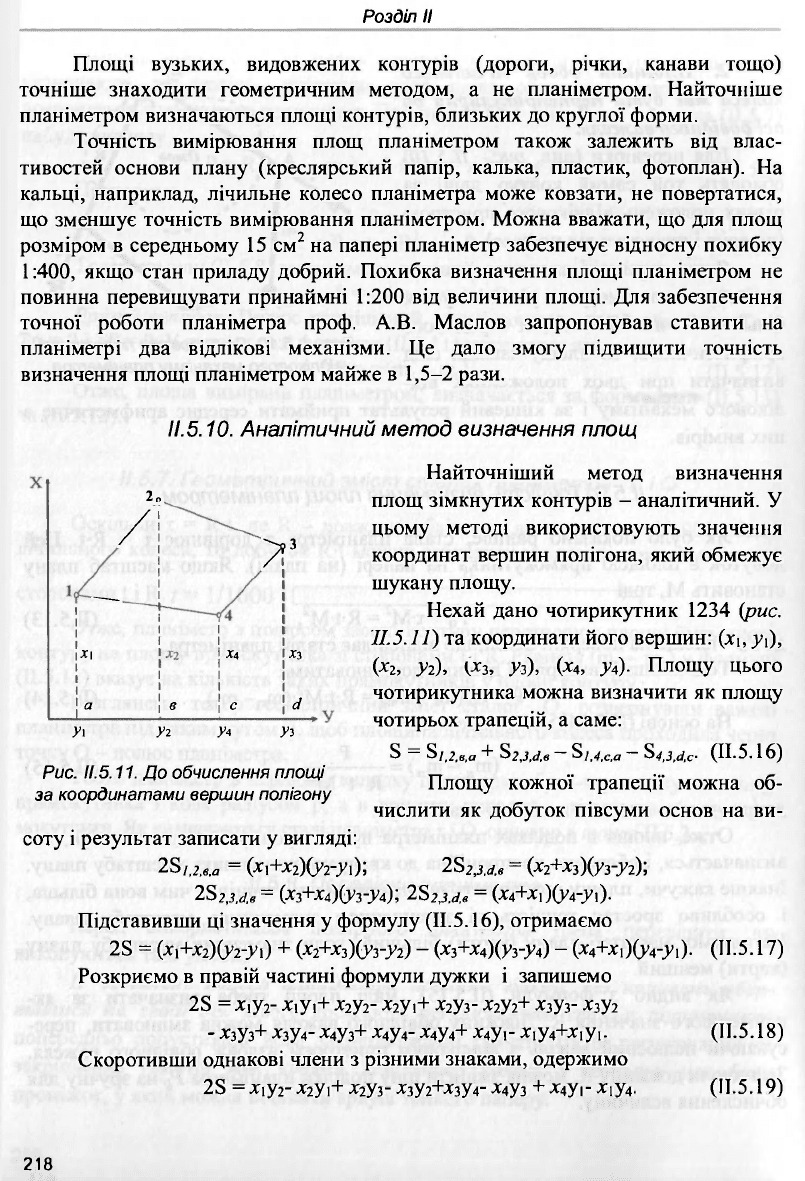
11.5.10.

Аналітичний метод визначення площ

Найточніший метод визначення

площ зімкнутих контурів - аналітичний. У

цьому методі використовують значення

координат вершин полігона, який обмежує

шукану площу.

Нехай дано чотирикутник 1234 (рис.

II.5.11) та координати його вершин: (хь^і),

(*2, Уі), Уз), (х

, У*)- Площу цього

чотирикутника можна визначити як площу

чотирьох трапецій, а саме:

S = Sl,2.e.a + S2,3,d.e ~

$1.4.с,а

S4,3,d,c-

(П.5. 16)

Площу кожної трапеції можна об-

числити як добуток півсуми основ на ви-

соту і результат записати у вигляді:

2S і,2,в.а = (Хі+Х

)(>2-Уі); 2S

2,3.d.e

= (х

+хз)(уз-у

);

2S2,ЗЛв =

(хз+х

)(уз-у

)-,

2S2,3.d.e = (х

+х,)(у

-_у,).

Підставивши ці значення у формулу (ІІ.5.16), отримаємо

2S = (хі+х

)(у

-уі) + (х2+хз)(уз-у

) - (х

+х

)(у

->>

) - (х

+хі)(>4-уі). (II.5.17)

Розкриємо в правій частині формули дужки і запишемо

2S = Х!у

- х,у,+ х

- х

у,+ х

- х

+ х

- х

- Х

+ х

- х

+ х

- х

+ х

у,- Хіу

+Х,уі. (II. 5.18)

Скоротивши однакові члени з різними знаками, одержимо

2S = хіу

- х

у,+ х

- х

+х

- х

+ x

Хіу

. (II.5.19)

Рис.

11.5.11.

До обчислення площі

за координатами вершин полігону

>218

Горизонтальнв знімання

Згрупуємо члени у формулі (II.5.19) так, щоб множниками були абсциси х,

й отримаємо

2S = х^-Уа) + х

(уі-у\) + хі(у

-у

) + ^(уі-^з), (II.5.20)

або ординати у

2S =у,(х

-х

) +у

(х,-х

) +у

(х

-х

) +у

(х

-х,). (ІІ.5.21)

Формули (ІІ.5.20) та (И.5.21) можна записати для будь-якого «-кутника у

вигляді

2S = Zx

i+1

-y

)

;

(II.5.22)

і=1

2S = Zy

(x,

-x

i+1

), (II.5.23)

І=1

У формулах і - номер точки w-кутника. За цими формулами можна виз

начати площу багатокутника. За однією - площу, а інша використовується для

контролю правильності обчислень.

Зрозуміло, що в аналітичному методі точність визначення площ залежим,

н основному від точності визначення координат вершин и-кутника.

11.5.10.

Визначення площ методом академіка Савича

Академік Савич запропонував точний метод вимірювання площ, за яким

не ниникають похибки визначення сталої планіметра т (точніше гт

, де т

іпаменник масштабу), а також усуваються похибки, пов'язані з деформаціями

паперу, на якому побудовано план чи карту. В результаті значно підвищується

ючиість вимірювань. Такий метод широко застосовують для значних площ,

наприклад, площ областей чи площі усієї країни.

Розглянемо суть методу. Нехай маємо площу ділянки Р, визначену

иіалітично. Це може бути, наприклад, трапеція аркуша карти. Площу трапецій

їй

ановлено аналітично за координатами чотирьох вершин.

Нехай на цій трапеції необхідно знайти площі ділянок, що входять у різи

оонасті, а саме ділянки Р

, Рз. Планіметром визначають площу всі< ї фігурі

рапеції та площі її частин Р

, Р

. Тоді можна записати:

P = x-(m

-m

); (115.24

Р, = т-(ші

- Ш|

); (II.5.25

= т(т

2к

- т

2п

); (II.5.26

Рз = х (ш

3і

< - т

„). (ІІ.5.27

2Н

Розділ II

Розділивши площу першої фігури на площу усієї трапеції, матимемо

р, т-(т, -т

1п

) (т

1к

-т, )

— = —-—- —, тому р, = р-—— —. (11.5.28)

Р t(m

-m

) K-m„)

Нагадаємо, що Р - відома площа, яку визначили за координатами вершин

грапеції аналітично.

Аналогічно знаходимо площі інших ділянок:

1=p

2°). (ІІ.5.29)

(т

-т

)

р,

р.

(т

3"~

3"). (II.5.ЗО)

(т

-т

)

З формул (ІІ.5.28), (ІІ.5.29), (ІІ.5.30) видно, що на ТОЧНІСТЬ визначення

площ фігур не впливає ТОЧНІСТЬ визначення сталої планіметра, а лише точність

обведення контурів обвідною точкою.

>220

РОЗДІЛ III. ВЕРТИКАЛЬНЕ ЗНІМАННЯ

111.1. Рельєф та його зображення на планах та картах

III. 1.1.

Абсолютні та умовні висоти.

Перевищення. Гзодезичні висоти

Рельєфом називається сукупність нерівностей місцевості. Найважли-

•> 11

ними параметрами рельєфу є висоти точок і перевищення. Зображаючи

р. ц.сф на планах та картах, спочатку треба знайти висоти точок місцевості га

перевищення.

Розглянемо рис. III.1.1, на якому показана частина фізичної поверхні

Землі та поверхня рівня моря у спокійному стані, уявно продовжена під

фііичною поверхнею Землі. Цю поверхню називають рівневою поверхнею

(,'еоїдом). На рисунку також наведено частину еліпсоїда. Рівневу поверхню

океанів і морів приймають за нуль абсолютних висот (точка О).

Рис.

III. 1.1.

Абсолютні та умовні висоти, геодезичні

висоти,

перевищення

Абсолютна висота точки А місцевості - це прямовисний відрізок ЛЛ' від

цієї точки на поверхні Землі до точки А' на рівневій поверхні.

Аналогічно абсолютною висотою точки В є прямовисний відрізок В В'.

Точка В розташована вище від точки А на величину прямовисного

підрізка, позначеного на рис.

III. 1.1

буквою /г. Це і є перевищення між точками

І і />'. Отже, перевищення між двома точками - це відстань по прямовисній лінії

між рівневими поверхнями, що проведені через ці точки, тобто перевищення

це різниця висот цих точок. Зауважимо, що рівневих поверхонь можна провести

безліч. На рис.

III. 1.1

показано рівневі поверхні точок А і В.

221