Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум
Подождите немного. Документ загружается.

4) в диалоговом окне
Корреляция
в поле «Входной интервал» необ-
ходимо ввести диапазон ячеек, содержащих исходные данные. Если вы-
делены и заголовки столбцов, то установить флажок «Метки в первой
строке» (рис. 4.2.2);
5) выберите параметры вывода. В данном примере - установите пере-
ключатель «Новый рабочий лист»;
6)
ОК.
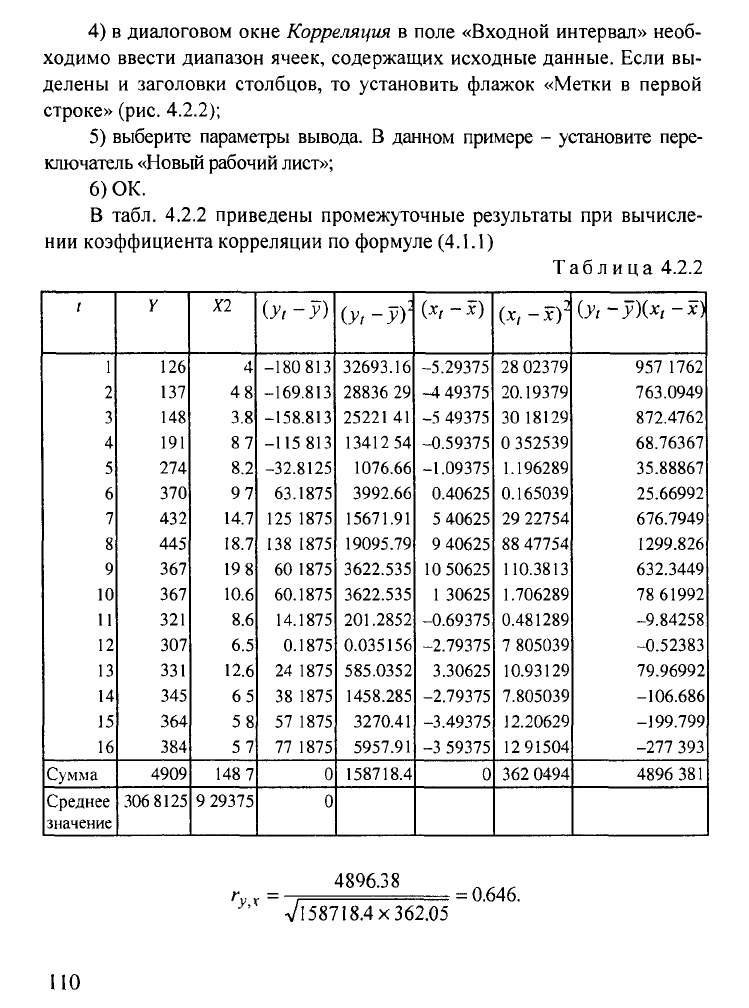
В табл. 4.2.2 приведены промежуточные результаты при вычисле-
нии коэффициента корреляции по формуле (4.1.1)
Таблица
4.2.2
t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Сумма
Среднее
значение
Y
126
137
148
191
274
370
432
445
367
367
321
307
331
345
364
384
4909
306
8125
Х2
4
48
3.8
87
8.2
97
14.7
18.7
19
8
10.6
8.6
6.5
12.6
65
58
57
148
7
9 29375
(y
t
-y)
-180 813
-169.813
-158.813
-115813
-32.8125
63.1875
125 1875
138 1875
60 1875
60.1875
14.1875
0.1875
24 1875
38 1875
57 1875
77 1875
0
0
(у<-уУ
32693.16
28836 29
2522141
13412 54
1076.66
3992.66
15671.91
19095.79
3622.535
3622.535
201.2852
0.035156
585.0352
1458.285
3270.41
5957.91
158718.4
(х,
- х)
-5.29375
-4
49375
-5 49375
-0.59375
-1.09375
0.40625
5 40625
9 40625
10 50625
1 30625
-0.69375
-2.79375
3.30625
-2.79375
-3.49375
-3 59375
0
(х,-х)
2
28 02379
20.19379
30 18129
0 352539
1.196289
0.165039
29 22754
88 47754
110.3813
1.706289
0.481289
7 805039
10.93129
7.805039
12.20629
12 91504
362 0494
(У/
~y)(x
t
-x)
957 1762
763.0949
872.4762
68.76367
35.88867
25.66992
676.7949
1299.826
632.3449
78 61992
-9.84258
-0.52383
79.96992
-106.686
-199.799
-277 393
4896 381
г
у,х ~
4896.38
Vl 58718.4x362.05
= 0.646.
ПО

1
| У
[Об
ьем ре
126
137
148
191
274
370
432
445
367
367
321
307
331
345
364
384
В
С
:
D '
Е
F G
I
Н
XI
/2 ХЗ Х4 Х5
Время Реклама Цена
Цена конкИндекс
потребительских расходов
1
4 15 17 100
2 48 148 173
984
Анализ данных
Инструменты
анализа
Однофакторный
дисперсионный анализ
Двухфакторныи дисперсионный анализ
с
повторениями
Двухфакторныи
дисперсионный анализ без повторений
Ковариация
Описательная статистика
Экспоненциальное сглаживание
Двухвыборочный
F-тест
для дисперсии
Анализ Фурье
Гистограмма
<Ж
Отмена
Справка
Рис. 4.2.2. Выбор инструмента Корреляция.
12
J
ц
хз
Реклама Цена
4
4.8
Х4
Х5
Цена конкИндекс потребительских
15
17 100
14.8*
17
3 98.4
!
Y
XI
Объем ре: Время
126
137
148
191
274
370
432
445
367
367
321
307
331
345
364
384
Рис. 4.2.3. Диалоговое окно
Корречяиш
подготовлено к выполнению анализа данных.
Корреляция
„
|
Входной
жтервая;
j Группирование:
А Г вводной
интервал:
J
(*
Новый
рабочий
диет;
i
J~
Новая рабочая книга
|$A$2'$F$18
(*
№
СТОлб&ам
С ш
строкам
1
1
t
:У
:
V :
—Mi
ИНЕЕ
<ж
Отмена
£ррзека
;
111
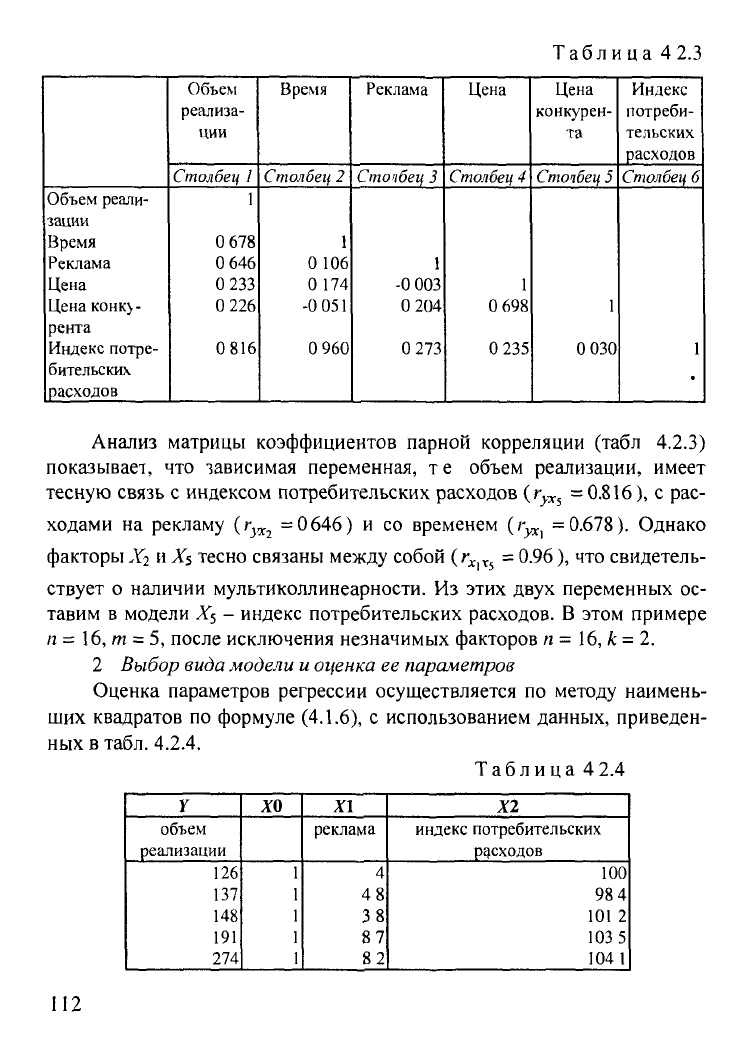
Таблица 4 2.3
Объем реали-
зации
Время
Реклама
Цена
Цена
конку-
рента
Индекс потре-
бительских
расходов
Объем
реализа-
ции
Столбец 1
1
0 678
0 646
0 233
0 226
0816
Время
Столбец 2
1
0 106
0 174
-0
051
0 960
Реклама
Сточбец 3
1
-0 003
0 204
0 273
Цена
Столбец
4
1
0 698
0 235
Цена
конкурен-
та
Сточбец
5
1
0 030
Индекс
потреби-
тельских
расходов
Столбец
6
1
Анализ матрицы коэффициентов парной корреляции (табл
4.2.3)
показывает, что зависимая переменная, т е объем реализации, имеет
тесную связь с индексом потребительских расходов
(г
№
=0.816),
с рас-
ходами на рекламу
(г
}ГХ2
=0646)
и со временем
(г^
=0.678). Однако
факторы
Хг и Х$
тесно связаны между собой
(г
Х]Х$
=
0.96),
что свидетель-
ствует о наличии мультиколлинеарности. Из этих двух переменных ос-
тавим в модели
Х
5
- индекс потребительских расходов. В этом примере
п = 16, т = 5, после исключения незначимых факторов п
=
16,
к
=
2.
2
Выбор вида модели
и
оценка
ее
параметров
Оценка параметров регрессии осуществляется по методу наимень-
ших квадратов по формуле (4.1.6), с использованием данных, приведен-
ных в табл. 4.2.4.
Таблица 4 2.4
Y
объем
реализации
126
137
148
191
274
Х0
XI
реклама
4
48
38
87
82
XI
индекс потребительских
расходов
100
98 4
101 2
103 5
104 1
112

Окончание
Y
объем
реализации
370
432
445
367
367
321
307
331
345
364
384
хо
XI
реклама
97
147
187
19 8
106
86
65
126
65
58
57
Х2
индекс потребительских
расходов
107
107 4
108 5
108 3
109 2
1101
1107
1103
111 8
1123
1129
«I
\
а
2)
'
1 1
*1,1 *12
V *2,1 *2,2
1
\
*2,16
)
*11
х
2,\
*1,2
х
22
1 1
*1 1
х
\2
Х
2Л
х
12
(Х
Т
Х) =
(Х
Т
Х)
1
Xl,l6*2
16,
'
16 148.7 1715.7
>
148.7 1744.03 16036.2 ,
,1715.7
16036.2
184282.13,
/
39.2314
0.06752
-0.3711 "\
0.06752 0.00299 -0.00088
-0.3711 -0.00088 0.00354
a
=
(X
1
Xy
l
X'
r
Y--
"о
<*2
1471.314^1
9568
15754
1
\
х
\16
*2,16
)
У\
)>2
.У\6
Уравнение регрессии зависимости объема реализации от затрат на
рекламу и индекса потребительских расходов можно записать в сле-
дующем виде:
Г =
-1471 314
+9.568Х]+
15.754Х
2
.
Расчетные значения Y определяются путем последовательной под-
становки в эту модель значений факторов, взятых для каждого момента
времени t
113

Применение
инструмента
Регрессия Для проведения регрессион-
ного анализа выполните следующие действия:
1)
выберите команду Сервис
=>Анализ
данных,
2) в диалоговом окне Анализ данных выберите инструмент Регрес-
сия (рис. 4.2.1), а затем щелкните на кнопке (Ж;
3) в диалоговом окне Регрессия в поле «Входной интервал Y» вве-
дите адрес одного диапазона ячеек, который представляет зависимую
переменную. В поле «Входной интервал X» введите адреса одного или
нескольких диапазонов, которые содержат значения независимых пере-
менных (рис. 4.2.4);
4) если выделены и заголовки столбцов, то установить флажок
Метки
в
первой
строке;
5) выберите параметры вывода. В данном примере - установите пе-
реключатель
«Новая рабочая
книга»;
6) в поле «Остатки» поставьте необходимые флажки;
7) ОК.
|Y Х1
106-ьем р{Реглли«
:
;
10
11
3
и
126<
ш!
ША
432<
445'
387"
397J
321J
3071
33lJ
3451
364t
384J
4
48
38
87
8 2
87
14 7
18 7
19
8
10
6
86
86
12 6
6S
58
57
Х4
Индекс
п|
100
88 4
1012
103.5
1041
1071
107
4;
108
6
L
108
з
«
f"
йэовень
надежности:
109 2 S
•
.<_-
Регрессия
-Входные данные
Вводной интервал
V:
Вводной интервал
X:
,
Р"&5етки
]$в$2 $c$ia
ПКаиетантв-нол»
|35
"
%
110.1
'
1107
1103
I
111
8
1123
1129
Параметры вывода -•
-
Г Выгодной
интервал!
(*
Новыйрабочийлист:
<• Новая рабочая
£г«*"а
Остатки -
уi
Р остатки
31
31
Отмена
ураека
Р
Срафикгатата»
к остатки i«
urn*'*
остатгое
Г"
Стандартаоеанные
остатки
Г"
Графиктдбора
-Нормальная
вероятность
Г"
График
нормальной
вероятности
Рис. 4.2.4 Диалоговое окно Регрессия подготовлено к выполнению
аначиза
данных
114
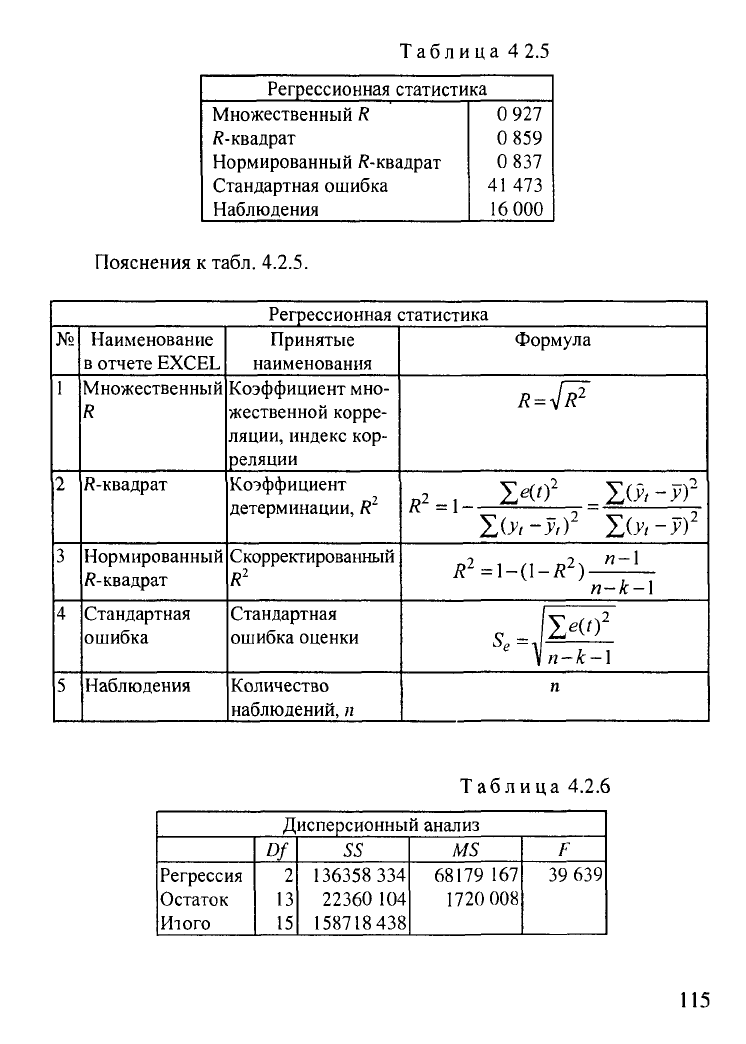
Таблица
4 2.5
Регрессионная статистика
Множественный
R
R-
квадрат
Нормированный /?-квадрат
Стандартная ошибка
Наблюдения
0
927
0
859
0
837
41
473
16
000
Пояснения к
табл.
4.2.5.
Регрессионная статистика
№
1
2
3
4
5
Наименование
в
отчете EXCEL
Множественный
R
/?-квадрат
Нормированный
/?-квадрат
Стандартная
ошибка
Наблюдения
Принятые
наименования
Коэффициент
мно-
жественной
корре-
ляции,
индекс
кор-
реляции
Коэффициент
детерминации,
R
2
Скорректированный
R
2
Стандартная
ошибка оценки
Количество
наблюдений,
п
Формула
R=4R
T
Л
2_!
1>(0
2
_^{y,-yf
КУ<-У,)
2
КУ,-У)
2
R
2
-\
(1 R
2
)
П
~
Х
п-к-\
s
-
|2>
(
°
2
п
Таблица
4.2.6
Дисперсионный анализ
Регрессия
Остаток
Итого
Df
2
13
15
SS
136358
334
22360
104
158718438
MS
68179
167
1720
008
F
39
639
15
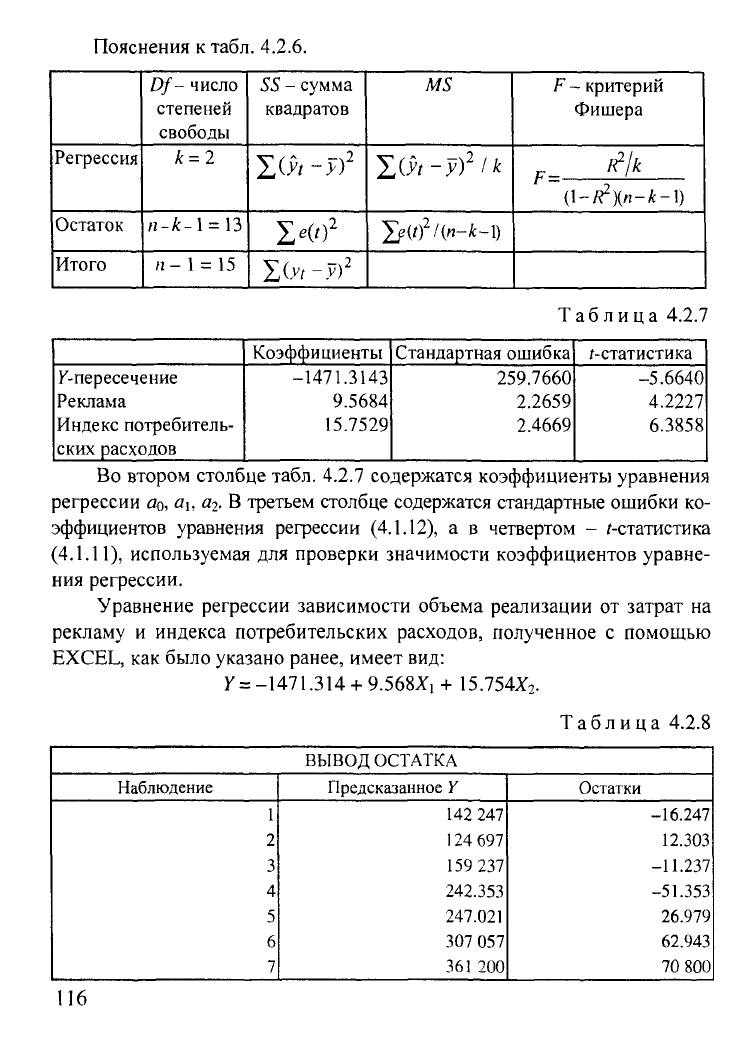
Пояснения к табл. 4.2.6.
Регрессия
Остаток
Итого
Df- число
степеней
свободы
к =
2
п-к-\ =
\Ъ
п-1 = 15
55 - сумма
квадратов
1СР/->)
2
le(tf
I(v/-v)
2
MS
l(yt-yf/k
Jf(t)
2
/(n-k-\)
F - критерий
Фишера
(\-FT)(n-k-\)
Таблица
4.2.7
У-пересечение
Реклама
Индекс потребитель-
ских расходов
Коэффициенты
-1471.3143
9.5684
15.7529
Стандартная ошибка
259.7660
2.2659
2.4669
/-статистика
-5.6640
4.2227
6.3858
Во втором столбце табл. 4.2.7 содержатся коэффициенты уравнения
регрессии
ао,
«ь
а
2
.
В третьем столбце содержатся стандартные ошибки ко-
эффициентов уравнения рефессии (4.1.12), а в четвертом - /-статистика
(4.1.11),
используемая для проверки значимости коэффициентов уравне-
ния регрессии.
Уравнение регрессии зависимости объема реализации от затрат на
рекламу и индекса потребительских расходов, полученное с помощью
EXCEL, как было указано ранее, имеет вид:
У
=-1471.314+
9.568Х,
+15.754*2.
Таблица 4.2.8
Наблюдение
1
2
3
4
5
6
7
ВЫВОД ОСТАТКА
Предсказанное
Y
142
247
124
697
159 237
242.353
247.021
307 057
361
200
Остатки
-16.247
12.303
-11.237
-51.353
26.979
62.943
70 800
116
Окончание
Наблюдение
8
9
10
11
12
13
14
15
16
ВЫВОД ОСТАТКА
Предсказанное Y
416 802
424.177
350.325
345.365
334.724
386.790
352 052
353 230
361 725
Остатки
28 198
-57.177
16.675
-24.365
-27 724
-55.790
-7.052
10 770
22 275
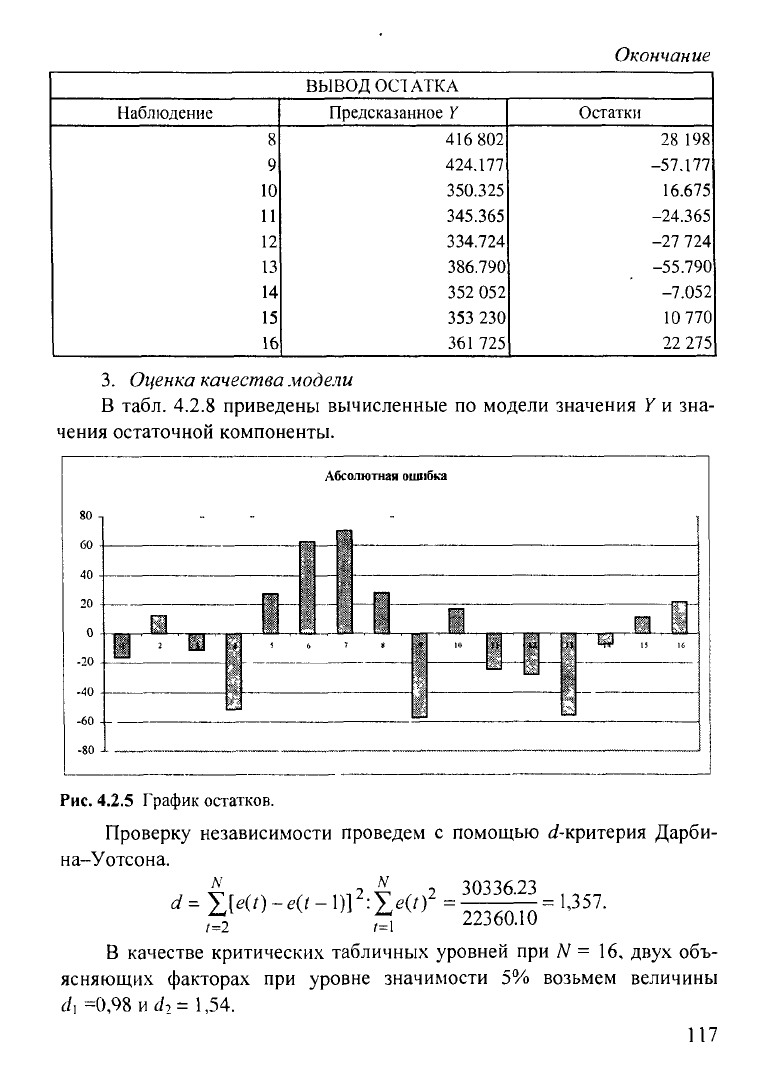
3.
Оценка качества модели
В табл. 4.2.8 приведены вычисленные по модели значения
У
и зна-
чения остаточной компоненты.
Рис. 4.2.5 График остатков.
Проверку независимости проведем с помощью
d-критерия
Дарби-
на-Уотсона.
В качестве критических табличных уровней при N = 16, двух объ-
ясняющих факторах при уровне значимости 5% возьмем величины
с/, =0,98 и
d
2
=
1,54.
117

Так как расчетное значение попало в интервал от
d\
до
d
2
,
то нельзя
сделать окончательный вывод по этому критерию. Для определения сте-
пени автокорреляции вычислим коэффициент автокорреляции
и
прове-
рим его значимость при помощи критерия стандартной ошибки.
Стандартная ошибка коэффициента корреляции рассчитывается
следующим образом:
Коэффициенты автокорреляции случайных данных обладают выбо-
рочным распределением, приближающимся
к
нормальному
с
нулевым
математическим ожиданием
и
средним квадратическим отклонением,
равным
l/л/й
=
l/л/Тб
=
0.25.
Если
г,
находится в интервале:
-1.96
•
0.25 <
г,
< 1.96
•
0.25,
то можно считать, что данные не показывают наличие автокорреляции
первого порядка, так как
-0.49 <
п
=
0.305
< 0.49,
и свойство независимости выполняется.
Вычислить для модели коэффициент детерминации
"
№
" ~Ъ(У,-У,)
2
~Ъ(У,-У)
2
~
= 1-22360.104/158718.44 = 136358.3/158718.44 = 0.859.
Он показывает долю вариации результативного признака под воздейст-
вием изучаемых факторов. Следовательно, около 86% вариации зависимой
переменной учтено в модели
и
обусловлено влиянием включенных факторов.
Проверку значимости уравнения регрессии произведем на основе
вычисления
F-критерия
Фишера:
F
=
#—
°'
859/2
-39.6.
(\-R
2
)/(n-k~\)
(l-0.859)/13
Табличное значение
F-критерия
при доверительной вероятности
0,95
Vi =
к
=
2
nv
2
=
n-k-
1
=
16-2-
1
=
13
составляет4.81.
Поскольку
F
pac
>
F
ra6l
,
уравнение регрессии следует признать
адекватным.
118

Значимость коэффициентов уравнения регрессии
а
ь
а
2
оценим с
использованием r-критерия Стьюдента.
t
aj
=a
J
/S
aj
=a
J
/s
e
xJb^,
'39.2314 0.06752
-0.3711 ^
(Х
Т
Х)'
1
=
0.06752 0.00299 -0.00088
ч
-0.3711
-0.00088 0.00354
,
Ь
22
= 0.00299,
&33
= 0.00354,
= 9.5684/2.2659
=
9.5684/41.473^0.00299
-4.223,
0|
t
ai
= 15.7529/2.4669
=
15.7529/41.473V0.00354
-6.3858.
Табличное значение r-критерия при уровне значимости 5% и степе-
нях свободы (16-2-1 = 13) составляет 1,77. Так как
t
pPC
>
t^n.
T0
коэф-
фициенты а\,
а
2
существенны (значимы).
4.
Проанализировать
влияние факторов на зависимую переменную
по
модели
(для
каждого коэффициента регрессии вычислить
коэффици-
ент
эластичности,
^-коэффициент)
Учитывая, что коэффициент регрессии невозможно использовать
для непосредственной оценки влияния факторов на зависимую перемен-
ную из-за различия единиц измерения, используем коэффициент эла-
стичности (Э) и
^-коэффициент,
которые соответственно рассчитыва-
ются по формулам:
JI
—
3|
•
Л
С
р
.
/
С
р,
Э,
=
9.568
•
9.294
/
306.813
=
0.2898;
Э
2
=
15.7529
•
107.231
/
306.813
=
5.506;
Р,
= а,
•
S
A(
:
S
h
где
S
v
=
J
2
У
«
N
-1
р,
=
9.568
•
4.913 / 102.865 = 0.457;
р
2
= 15.7529
•
4.5128 / 102.865 =
0.691.
Коэффициент эластичности показывает, на сколько процентов из-
меняется зависимая переменная при изменении фактора на
1
%.
119
